Unit 3: Change and The Metric System
Topic C: The Metric System
When you measure something, you are comparing. Measurement is comparing something with a standard unit of measure.
In the past, units of measure were based on things found in a community. Often, lengths of parts of the body were used to measure:
- Inch: the width of a thumb
- Span: the distance from tip of thumb to tip of little finger when the hand is spread out
- Foot: the distance from big toe to heel of foot
- Yard (becomes “rod): the distance from tip of nose to tip of thumb of an outstretched hand and arm
- Cubit: the distance from the tip of the middle finger to the elbow
- Fathom: the distance from the tip of one hand to the tip of the other with both arms stretched out
- Mile: 1000 military double steps in the Roman army (mile passuum means “1000 paces”)
The problem with these units was the distances would be different based on the size of the person doing the measuring. The problem grew even more when trade was started between cities.
Over a long period of time, people in different countries came up with different standard units of measure.
The British came up with imperial units such as inch, foot, yard and mile.
The French came up with metric units such as metre, centimetre, litre and gram. In Canada, we use both metric and imperial units.
Measuring Length
The basic unit of measure for length is the metre (abbreviation m). If you stretch your arm straight out beside you, a metre is about the distance from the tip of your nose to the tip of your middle finger.
Exercise 1
Consider the following distances. Answer yes or no if you would use a metre to measure. Check your work using the answer key at the end of the exercise.
Example:
- The length of a table – Yes
- The width of your watchband – No
- length of your classroom
- thickness of a piece of paper
- length of your pen or pencil
- height of the door
- distance from Prince George to Fort Nelson
- the width of your baby finger
- the size of a postage stamp
- the thickness of a quarter
- the length of the hallway outside your classroom
- the distance from your home to college
- the height of your coffee mug
- the width of your book
- the distance from your home to Moncton, New Brunswick
- the length of a city bus
Answers to Exercise 1
- yes
- no
- no
- yes
- no
- no
- no
- no
- yes
- no
- no
- no
- no
- yes
Exercise 2
Estimate the length of each item. Remember a metre is about the distance from the tip of your nose to the tip of your middle finger when your arm is stretched out beside you. Be sure to include the unit of measure in your answer. Have your instructor check your work.
- the height of the doorway
- the height of your table
- the width of the doorway
- the length of your arm
- the distance from the floor to hip
- the distance from the floor to waist
- the height of the ceiling
- the width of the window
- the length of your classroom
- the width of your classroom
Exercise 3
Circle the most reasonable measure. Remember a metre is about the distance from the tip of your nose to the tip of your middle finger when your arm is stretched out beside you. Check your work using the answer key at the end of the exercise.
- A person’s height
- 2m
- 20m
- 200m
- The height of a child
- 10 m
- 100 m
- 1 m
- The length of a house
- 150 m
- 15 m
- 1 m
- The length of a bed
- 200 m
- 2 m
- 20 m
- The height of a building
- 1 m
- 100 m
- 10 m
- The height of a refrigerator
- 20 m
- 200 m
- 2 m
Answers to Exercise 3
- i
- iii
- ii
- ii
- ii
- iii
Measuring Small Lengths and Long Distances
It is hard to measure small things using a metre. To measure small things, you can use centimetre (cm) or millimetre (mm).
A centimetre (cm) is about the width of your baby finger. Remember it is just a guide. A millimetre (mm) is about the thickness of your fingernail.
It is hard to measure long distances using a metre. To measure long distances, you can use kilometre (km). A kilometre is 1000 metres.
Exercise 4
For each item, circle the unit of measure you would use. Check your work using the answer key at the end of the exercise
| Item | Unit of Measure | |
|---|---|---|
| a) | the width of a room | m, cm, mm |
| b) | the thickness of a coin | m, cm, mm |
| c) | the length of your pencil | m, cm, mm |
| d) | the length of the hall | m, cm, mm |
| e) | the length of this page | m, cm, mm |
| f) | the length of a screw | m, cm, mm |
| g) | the height of your cup | m, cm, mm |
| h) | the length of a bus | m, cm, mm |
| i) | the thickness of a window pane | m, cm, mm |
| j) | the width of a chair | m, cm, mm |
Answers to Exercise 4
- m
- mm
- cm
- m
- cm
- mm
- cm
- m
- mm
- cm
Exercise 5
For each item, circle the letter of the most reasonable unit of measure. Check your work using the answer key at the end of the exercise.
- The width of a doorway
- 50 mm
- 1 m
- 50 m
- The length of your pencil
- 20 m
- 20 mm
- 20 cm
- The height of a tall building
- 1 m
- 100 m
- 10 m
- The height of a refrigerator
- 20 m
- 200 m
- 2 m
- The diameter of a quarter
- 24 mm
- 24 cm
- 24 m
- The height of the kitchen counter
- 9 m
- 9 cm
- 90 cm
- The distance around your wrist
- 15 mm
- 15 cm
- 15 m
- The width of a small TV screen
- 28 mm
- 128 cm
- 28 m
- The length of a car
- 5 m
- 5 cm
- 5 mm
- The height of a bookcase
- 2 cm
- 2 mm
- 2 m
Answers to Exercise 5
- ii
- iii
- ii
- iii
- i
- iii
- ii
- ii
- i
- iii
Exercise 6
Fill in the blank with the most reasonable unit of measure. Check your work using the answer key at the end of the exercise
- Most hand held calculators are about 15 long.
- The CN Tower in Toronto is 555 tall.
- Many young men have an 80 waist.
- Computer monitor screens are 28 wide.
- The handle of a hammer is 20 long.
- A table is about 65 long.
- The seat of a chair is about 30 above the floor.
- The window is about 3 long.
- A roll of tape is about 13 wide.
- A rope is about 7 thick.
Answers to Exercise 6
- cm
- m
- cm
- cm
- cm
- cm
- cm
- m
- mm
- mm
Measuring Capacity (Volume)
Volume is a measure of how much space something takes up. The basic unit of measure for volume is the Litre (L).
Can you think of two things that we buy in litres? We buy gasoline and milk in litres.
We use millilitres (mL) to measure small volumes. For example, a small cup of coffee is about 180 mL. Can you think of two things we buy in mL?
Exercise 7
Write the unit of measure you would use to measure each item (L or mL). Check your work using the answer key at the end of the exercise.
- Bottle of pop
- Gasoline
- Car window wash
- Can of beans
- Large bottle of juice
- Liquid dish soap
- Cough syrup
- Mixing bowls
- Ketchup
- Shampoo
- Vinegar
- Bathtub
- Ice cube tray
- Paint
Answers to Exercise 7
- mL
- L
- L
- mL
- L
- mL or L
- mL
- L
- mL or L
- mL
- L
- L
- mL
- L
Exercise 8
Circle the letter of the most reasonable unit of measure. Check your work using the answer key at the end of the exercise.
- A can of soup
- 3 L
- 30 mL
- 300 mL
- A large container of ice cream
- 5 L
- 500 L
- 50L
- A hot water heater
- 200 mL
- 50 L
- 200 L
- A cup of tea
- 18 mL
- 180 mL
- 218 L
- A garbage can
- 120 L
- 120 mL
- 12 L
- A saucepan
- 2 L
- 20 L
- 2 mL
- A dose of cough syrup
- 40 L
- 4 mL
- 40 mL
- The gas tank of a car
- 500 mL
- 5 L
- 50 L
- A jar of mustard
- 150 mL
- 15 L
- 15 mL
- A large mixing bowl
- 6 mL
- 60 L
- 6 L
Answers to Exercise 8
- iii
- i
- iii
- ii
- i
- i
- ii
- iii
- i
- iii
Measuring Mass
Mass is a measure of matter in something. The basic unit of measure for mass is the gram (g). We buy sliced meats, bulk food, spices and cereal in grams.
We use kilogram (kg) to measure the mass of large things such as cars, people, flour and sugar. Can you think of two things that we buy in kilograms?
We use milligram (mg) to measure the mass of small things such as medicine or vitamins. A milligram is very small. Can you think of two things that we buy in milligrams?
Exercise 9
Circle the unit of measure you would use to measure each item. Check your work using the answer key at the end of the exercise
| Item | Unit of Measure | |
|---|---|---|
| a) | pasta | mg, g, kg |
| b) | vitamin C | mg, g, kg |
| c) | peanut butter | mg, g, kg |
| d) | flour | mg, g, kg |
| e) | nails | mg, g, kg |
| f) | dry dog food | mg, g, kg |
| g) | rice | mg, g, kg |
| h) | cookies | mg, g, kg |
| i) | apples | mg, g, kg |
| j) | spices | mg, g, kg |
| k) | cement | mg, g, kg |
| l) | medicine tablets | mg, g, kg |
| m) | the family pet | mg, g, kg |
| n) | a coin | mg, g, kg |
Answers to Exercise 9
- g or kg
- mg
- g or kg
- kg
- kg
- kg
- kg
- g
- kg
- g
- kg
- mg
- kg
- g
Exercise 10
Circle the letter of the most reasonable unit of measure. Check your work using the answer key at the end of the exercise.
- A nickel
- 5 kg
- 5 g
- 50 g
- A small television
- 8 g
- 8 kg
- 80 g
- A flashlight battery
- 8 g
- 8 kg
- 80 g
- A baby
- 30 kg
- 3 kg
- 300 kg
- A dinner fork
- 50 g
- 5 g
- 5 kg
- A slice of bread
- 2 g
- 20 g
- 2 kg
- A sugar cube
- 2 mg
- 20 g
- 2 g
- A refrigerator
- 120 g
- 120 kg
- 12 kg
- A bag of potatoes
- 5 g
- 5 kg
- 50 mg
- A car
- 100 kg
- 1000 kg
- 10 kg
- A chocolate bar
- 300 mg
- 300 mg
- 300 g
- A back pack
- 12 kg
- 12 g
- 12 mg
Answers to Exercise 10
- ii
- ii
- i
- ii
- i
- ii
- iii
- ii
- ii
- ii
- iii
- i
Metric Prefixes
In the metric system a prefix is used to tell if something is large or small. A prefix is a part of a word that is added to the start of word to change the meaning.
The base units of measure in the metric system are the metre (m), litre (L) and gram (g).
If the prefix kilo is added to one of the base units of measures, such as kilometre or kilogram, you know that these are large amounts.
A kilometre is 1000 metres.
A kilogram is 1000 grams.
If the prefix centi or milli is added to one of the base units of measure, such as centimetre or milligram, you know that these are small amounts.
It takes 100 centimetres to make a metre. It takes 1000 milligrams to make a gram.
| Measures | Large | Base | Small |
|---|---|---|---|
| length | kilometre (km) | metre (m) | centimetre (cm) millimetre (mm) |
| volume | litre (L) | millilitre (mL) | |
| mass | kilogram (kg) | gram (g) | milligram (mg) |
Exercise 11
Write large, small or base on the line. Check your work using the answer key at the end of the exercise.
- kilometre .
- millimetre .
- metre .
- gram .
- litre .
- millimetre .
- milligram .
- kilogram .
- centimetre .
Answers to Exercise 11
- large
- small
- base
- base
- base
- small
- small
- large
- small
Exercise 12
Write the base unit of measure and then the prefix if one is needed. Check your work using the answer key at the end of the exercise.
| Item | Base | Prefix (if needed) | |
|---|---|---|---|
| a) | Height of a tree | ||
| b) | A bottle of vanilla | ||
| c) | A cold tablet | ||
| d) | Distance between Vancouver and Toronto | ||
| e) | Thickness of a piece of paper | ||
| f) | Length of your foot | ||
| g) | Length of a piece of lumber | ||
| h) | A bottle of hand lotion | ||
| i) | A granola bar | ||
| j) | Diameter of a DVD | ||
| k) | Mass of a book | ||
| l) | Water in a hot tub | ||
| m) | Distance around the Earth | ||
| n) | Gap in a spark plug |
Answers to Exercise 12
| Item | Base | Prefix (if needed) | |
|---|---|---|---|
| a) | Height of a tree | m | |
| b) | A bottle of vanilla | L | milli |
| c) | A cold tablet | g | milli |
| d) | Distance between Vancouver and Toronto | m | kilo |
| e) | Thickness of a piece of paper | m | milli |
| f) | Length of your foot | m | centi |
| g) | Length of a piece of lumber | m | |
| h) | A bottle of hand lotion | L | milli |
| i) | A granola bar | g | |
| j) | Diameter of a DVD | m | centi |
| k) | Mass of a book | g | |
| l) | Water in a hot tub | L | |
| m) | Distance around the Earth | m | kilo |
| n) | Gap in a spark plug | m | milli |
Exercise 13
Write the unit of measure you would use for each item below. Check your work using the answer key at the end of the exercise.
- coffee in a cup – millilitres (mL)
- bag of potatoes
- gas for a car
- length of the hall
- vitamin C tablet
- thickness of glass
- width of a page
- box of cereal
- distance from Vancouver to Halifax
- height of a child
- can of soup
- window wash for the car
- dose of heart medicine
- length of a machine bolt
- cheese
Answers to Exercise 13
- coffee in a cup – millilitres (mL)
- bag of potatoes – kilogram (kg)
- gas for a car – litre (L)
- length of the hall – metre (m)
- vitamin C tablet – milligram (mg)
- thickness of glass – millimetre (mm)
- width of a page – centimetre (cm)
- box of cereal – gram (g)
- distance from Vancouver to Halifax – kilometre (km)
- height of a child – metre (m)
- can of soup – millilitre (mL)
- window wash for the car – litre (L)
- dose of heart medicine – milligram (mg)
- length of a machine bolt – millimetre (mm)
- cheese – kilogram (kg) or gram (g)
Area of Rectangles and Squares
Area is the amount of surface within a figure. Area is described using square units.
For example,
- If the figure is a room, the area is the floor surface.
- If the figure is a tabletop, the area is the top surface of the table. If the figure is a roof, the area would be the shingled surface.
- If the figure is property, the area is the ground within the property lines.
- If the figure is this page, the area is the entire flat page that you are reading.
Example A
Find the area of this rectangle.
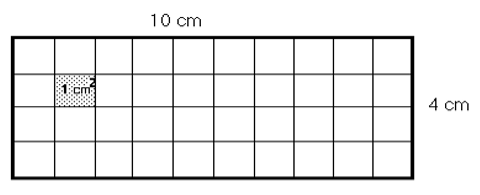
The measurements of this rectangle are given in centimetres. To measure the area, we will use squares which are 1 cm by 1 cm ( a square centimetre). How many square centimetres will fit on the surface of this rectangle? Count the 1 cm squares drawn within the Example A rectangle.
The area of this rectangle is square centimetres.
This is written as cm2
Square centimetres is usually written cm2 which is said as “square centimetres” or “centimetres squared”. The small number is called an exponent and if the exponent is 2, it means multiplied by itself, so cm2 means [latex]\text{cm}\times \text{cm}[/latex].
Square kilometres are written km2. Square metres are written m2.
Example B
This is a diagram of a large cattle ranch. The measurements of the ranch are shown as kilometres. What is the area of this ranch?
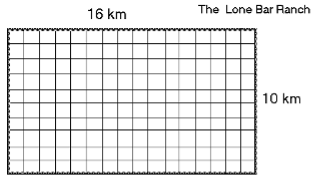
The square units to measure will be square kilometres. The area of this ranch will be the number of units 1 km by 1 km (km2). The diagram shows how many square kilometres would fit in an area 16 km by 10 km. Count them. The area of the Lone Bar Ranch is km2.
Did you find a quick method for counting the square units? Did you multiply the number of rows by the number of square kilometres in each row? The quick method of finding the area of a rectangle is to multiply the length by the width.
Use this formula to find the area of a rectangle:
[latex]\text{Area of a rectangle} = \text{length (}l\text{)} \times \text{width (}w\text{)}[/latex]
Length times width can also be expressed as lw,
so [latex]\text{A}_{\text{rectangle}}= lw[/latex]
The answer must be expressed in square units.
Example C
Give the area of a soccer field that is 100 m by 45 m.
Arectangle = lw
[latex]\text{Area of the soccer field} = 100 \text{ m} \times 45 \text{ m} = 4500 \text{ m}^2[/latex]
Exercise 14
Find the area of the rectangles described below. The measures of the length (l) and the width (w) have been given. Draw and label a picture for each. Be sure to write the unit of measure for each answer. Check your work using the answer key at the end of the exercise.
- [latex]l = 10 \text{ cm}[/latex], [latex]w = 6 \text{ cm}[/latex]
- [latex]l = 100 \text{ km}[/latex], [latex]w = 70 \text{ km}[/latex]
- [latex]l = 400 \text{ km}[/latex], [latex]w = 100 \text{ km}[/latex]
- [latex]l = 975 \text{ cm}[/latex], [latex]w = 35 \text{ cm}[/latex]
- [latex]l = 196 \text{ cm}[/latex], [latex]w = 28 \text{ cm}[/latex]
- [latex]l = 82 \text{ km}[/latex], [latex]w = 12 \text{ km}[/latex]
- [latex]l = 60 \text{ cm}[/latex], [latex]w = 250 \text{ cm}[/latex]
- [latex]l = 90 \text{ cm}[/latex], [latex]w = 2 \text{ cm}[/latex]
Answers to Exercise 14
- [latex]60 \text{ cm}^2[/latex]
- [latex]7000 \text{ km}^2[/latex]
- [latex]40000 \text{ km}^2[/latex]
- [latex]34125 \text{ cm}^2[/latex]
- [latex]5488 \text{ cm}^2[/latex]
- [latex]984 \text{ km}^2[/latex]
- [latex]1500 \text{ cm}^2[/latex]
- [latex]180 \text{ cm}^2[/latex]
Squares are rectangles with all four sides congruent (the same length). So to find the area of a square you still use the same formula of multiplying the length times the width. But since the length and the width of a square are the same, you are multiplying the measure of the side (s) by itself. The formula for finding the area of a square is often written using an exponent.
Asquare = s2
For example, to find the area of a square piece of property, multiply the length of one side by itself. If the measure of one side of a property is 75 m,
Area of this piece of property: [latex]75^2 = 75\text{ m} \times75\text{ m} = 5625\text{ m}^2[/latex]
Exercise 15
Find the area of the squares. The measure of the side has been given. Draw and label a picture for each. Be sure to write the unit of measure for each answer. Check your work using the answer key at the end of the exercise.
- Asquare, if [latex]s = 5 \text{ cm}[/latex]
- Asquare, if [latex]s = 125 \text{ km}[/latex]
- Asquare, if [latex]s = 45 \text{ mm}[/latex]
- Asquare, if [latex]s = 100 \text{ m}[/latex]
- Asquare, if [latex]s = 14 \text{ km}[/latex]
- Asquare, if [latex]s = 25 \text{ cm}[/latex]
Answers to Exercise 15
- [latex]25 \text{ cm}^2[/latex]
- [latex]15625 \text{ km}^2[/latex]
- [latex]2025 \text{ mm}^2[/latex]
- [latex]10000 \text{ m}^2[/latex]
- [latex]196 \text{ km}^2[/latex]
- [latex]625 \text{ cm}^2[/latex]
Problems Using Area
Exercise 16
Do these problems by following the five problem-solving steps. Be sure to draw a picture. Check your work using the answer key at the end of the exercise.
- A garden in the shape of a rectangle is 34 m long and 20 m wide. What is the area of the garden?
- Mr. Pavelski has a lot in the shape of a square. If the side of his square lot is 50 m, what is the area of the lot?
- A rectangular board is 58 cm wide and 64 cm long. How much area will this board cover?
- Kyoko bought some curtain material that is 198 cm long and 40 cm wide. How many square centimetres of material did she buy?
- The distance between bases of a baseball diamond (a square) is 27 m. What is the area of the baseball diamond?
- The janitor waxed a floor that was 24 m long and 18 m wide. How many square metres of floor did he wax?
Answers to Exercise 16
- [latex]680 \text{ m}^2[/latex]
- [latex]2500 \text{ m}^2[/latex]
- [latex]3712 \text{ cm}^2[/latex]
- [latex]7920 \text{ cm}^2[/latex]
- [latex]729 \text{ m}^2[/latex]
- [latex]432 \text{ m}^2[/latex]
Perimeter and Area of Rectangles and Squares
Rectangle
Perimeter means distance around. To find the perimeter of a rectangle, use the formula
[latex]P = 2 \times \text{length} + 2 \times \text{width}[/latex].
Example D
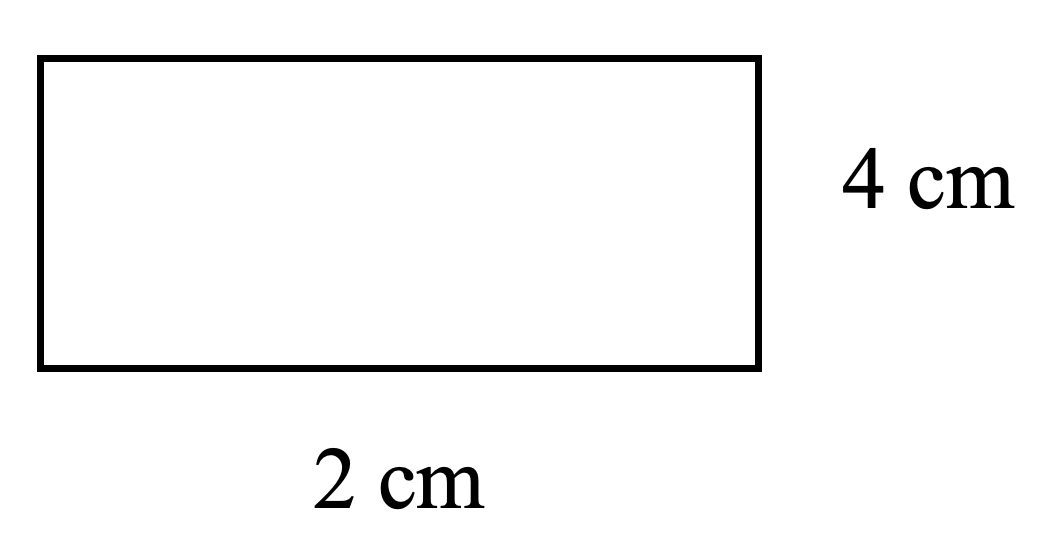
[latex]\begin{array}{l}P = 2 \times \text{length} + 2 \times \text{width} \\\hspace{1em} = 2\times 4 \text{ cm}+ 2 \times 2 \text{ cm}\\ \hspace{1em}= 8 \text{ cm}+4 \text{ cm}\\ \hspace{1em}=12 \text{ cm}\end{array}[/latex]
Remember: Multiply first and then add.
Area means the amount of surface within a shape. To find the area of a rectangle, use the formula
[latex]A = \text{length} \times \text{width}[/latex]
Example E
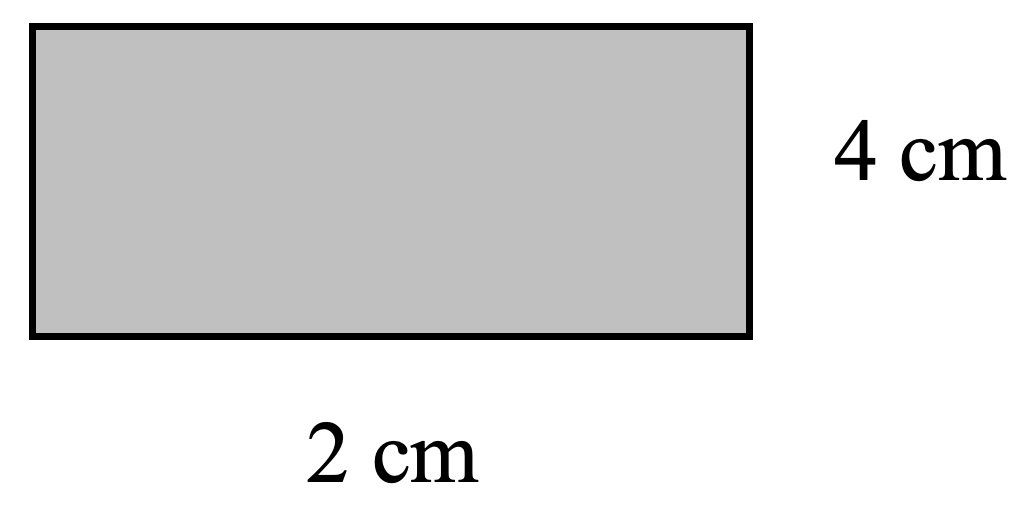
[latex]\begin{array}{l}A = \text{length} \times \text{width} \\\hspace{1em} = 4 \text{ cm}\times 2 \text{ cm}\\\hspace{1em} = 8 \text{ cm}^2 \end{array}[/latex]
Exercise 17
For each rectangle, find both the perimeter (distance around) and the area (amount of surface within). Check your work using the answer key at the end of the exercise.
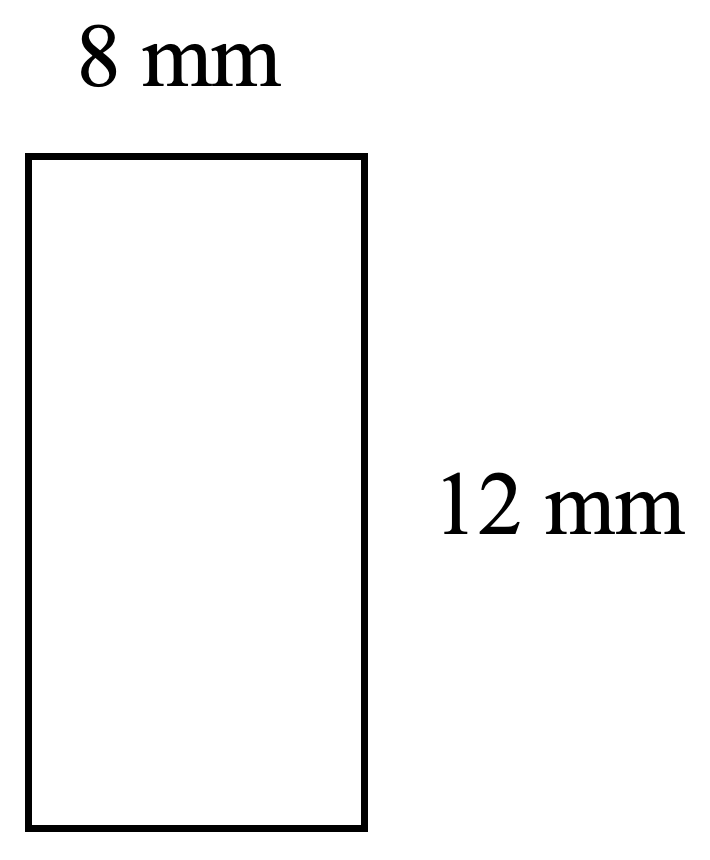
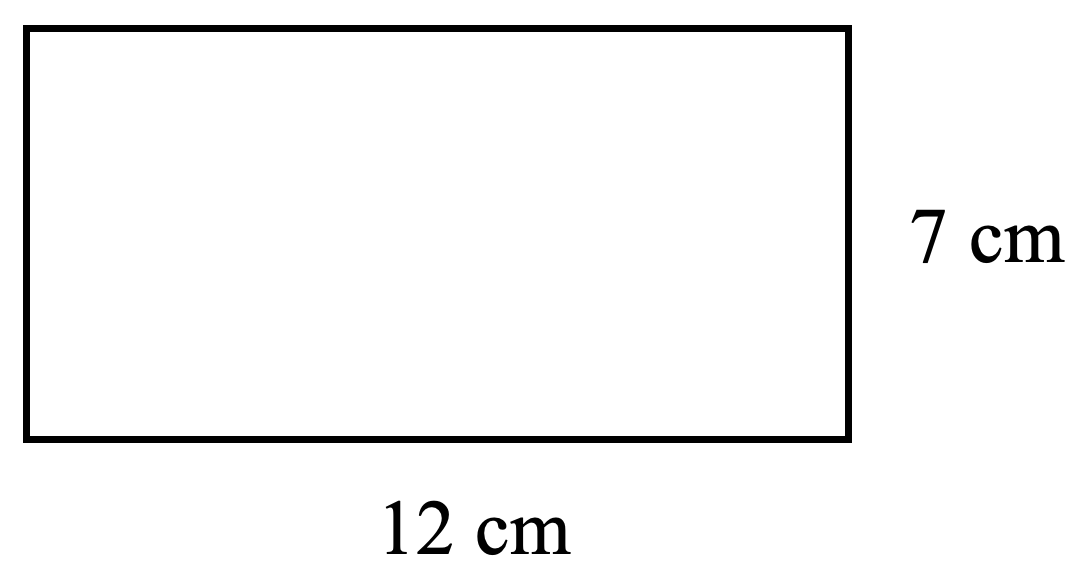
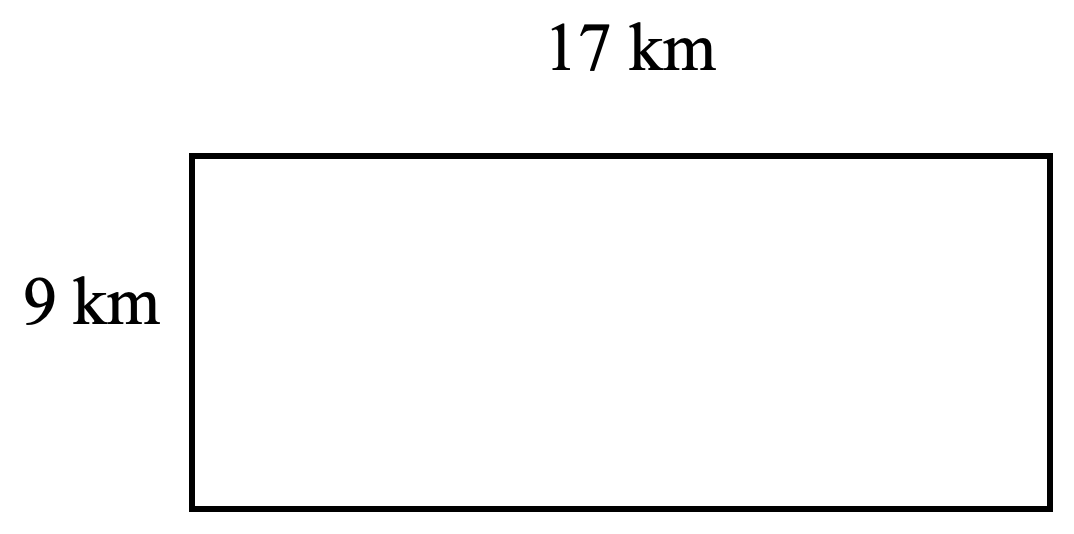

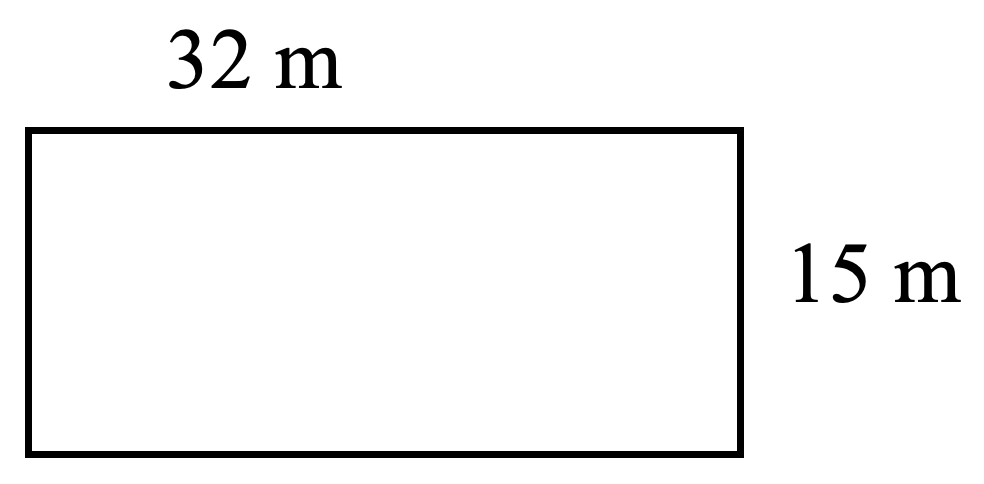
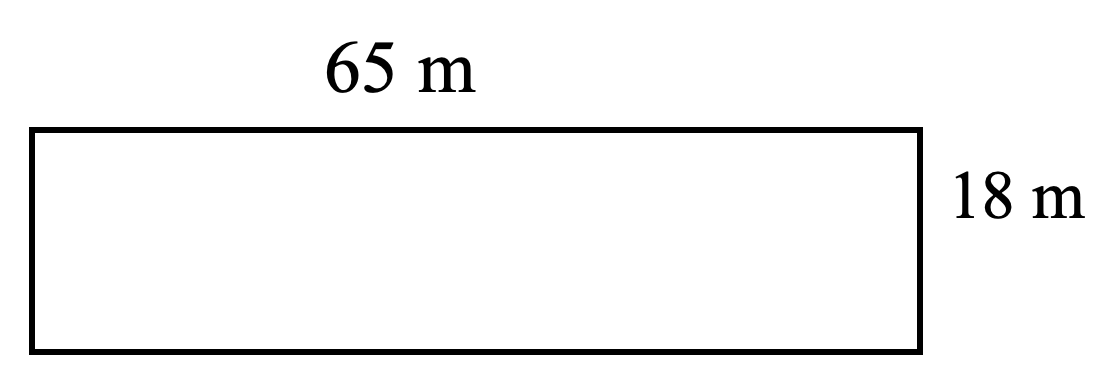
- Raoul’s lot is shaped like a rectangle. If it is 55 m long and 15 m wide, what is the perimeter and area of his lot?
- The playground is shaped like a rectangle. Its length is 140 m and its width is 60 What is the perimeter and area of the playground?
Answers to Exercise 17
- P = 16 m, A = 12 m2
- P = 38 cm, A= 84 cm2
- P = 52 km, A = 153 km2
- P = 40 mm, A 96 mm2
- P = 94 m, A = 480 m2
- P – 166 m, A = 1170 m2
- P = 140 m, A = 825 m2
- P = 400 m, A = 8400 m2
Square
Perimeter means distance around. To find the perimeter of a square, use the formula
P = 4 × side or Psquare = 4s
Example F
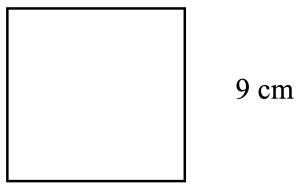
[latex]\begin{array}{l}P = 4\times \text{side} \\\hspace{1em} = 4 \times 9 \text{ cm}\\\hspace{1em} = 36 \text{ cm}\end{array}[/latex]
Area means the amount of surface within a shape. To find the area of a square, use the formula
A = side2 or Asquare = s2
Example G
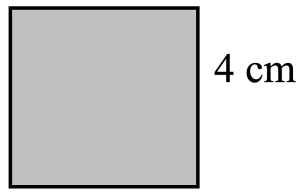
[latex]\begin{array}{l}A = \text{side}^2 \\\hspace{1em} = (4 \text{ cm})^2\\\hspace{1em} = 16 \text{ cm}^2\end{array}[/latex]
Exercise 18
For each square, find both the perimeter (distance around) and the area (amount of surface within). Check your work using the answer key at the end of the exercise.
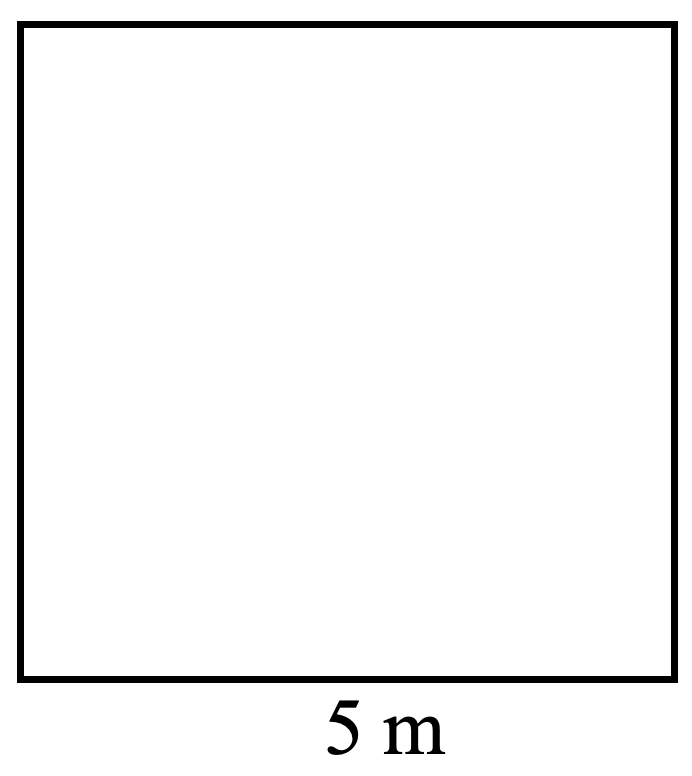
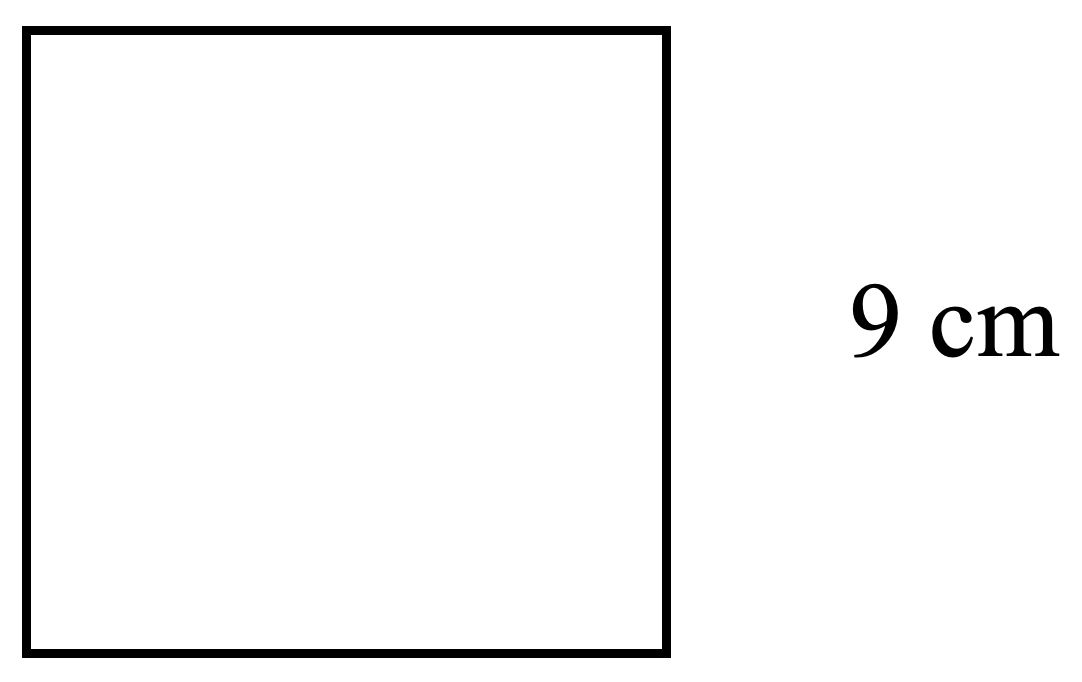
-

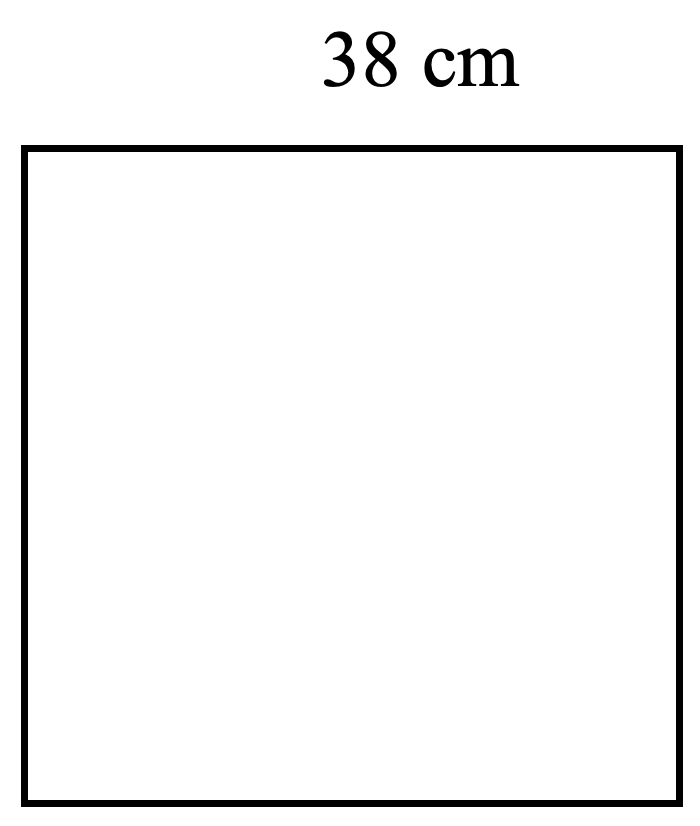
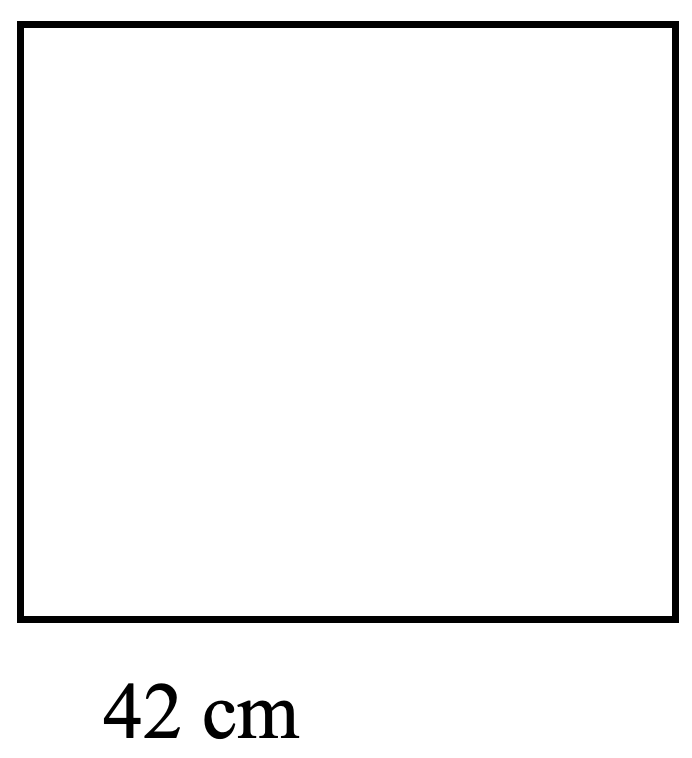
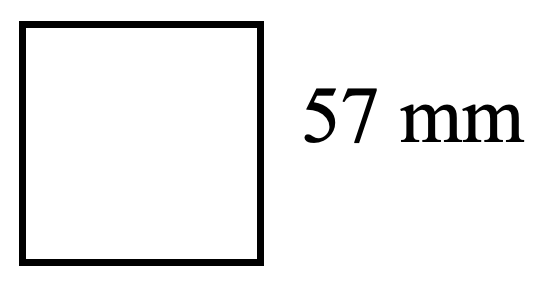
- Luisa bought a 115 cm square tablecloth. What is the perimeter and area of the tablecloth?
- Liang bought a square tarp whose side was 31 m. What is the perimeter and area of the tarp?
Answers to Exercise 18
- P = 20 m, A = 25 m2
- P = 36 cm, A= 81 cm2
- P = 60 cm, A = 255 cm2
- P = 152 cm, A = 1444 cm2
- P = 168 cm, A = 1764 cm2
- P – 288 mm, A = 3249 mm2
- P = 460 cm, A = 13225 cm2
- P = 124 m, A = 961 m2
Topic C: Self Test
Mark /38 Aim 30/38
- For each item, circle the unit of measure you would use. (8 marks)
Item Unit of Measure a) Height of a doorknob above the floor m, cm, mm, km b) Thickness of a piece of wire m, cm, mm, km c) Length of a ski m, cm, mm, km d) Thickness of a piece of string m, cm, mm, km e) Height of a fence m, cm, mm, km f) Length of a finger m, cm, mm, km g) Length of a football field m, cm, mm, km h) How far you travelled on your holiday m, cm, mm, km - Circle the letter of the most reasonable measure. (6 marks)
- Storage box
- 66 mL
- 66 L
- 6 L
- Baby Shampoo
- 593 mL
- 593 L
- 59 L
- Antifreeze
- 40 L
- 4 L
- 40 mL
- Wastebasket
- 42 mL
- 4 L
- 42 mL
- Deodorant
- 354 L
- 35 mL
- 354 mL
- Liquid laundry soap
- 975 mL
- 97 L
- 975 L
- Storage box
- Circle the unit of measure you would use. (6 marks)
Item Unit of Measure a) can of peanuts mg, g, kg b) cat litter mg, g, kg c) an antacid tablet mg, g, kg d) bag of potato chips mg, g, kg - Fill in the chart with the right metric prefix. (6 marks)
Measure
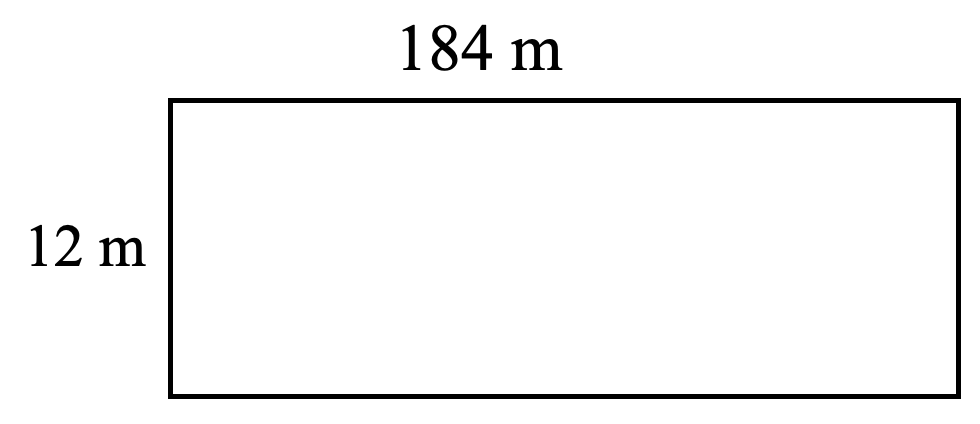
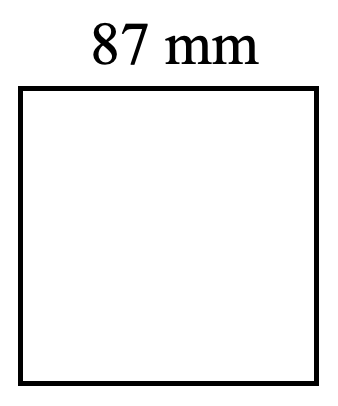
Small Base Large - Find the perimeter and area for each shape. (12 marks)
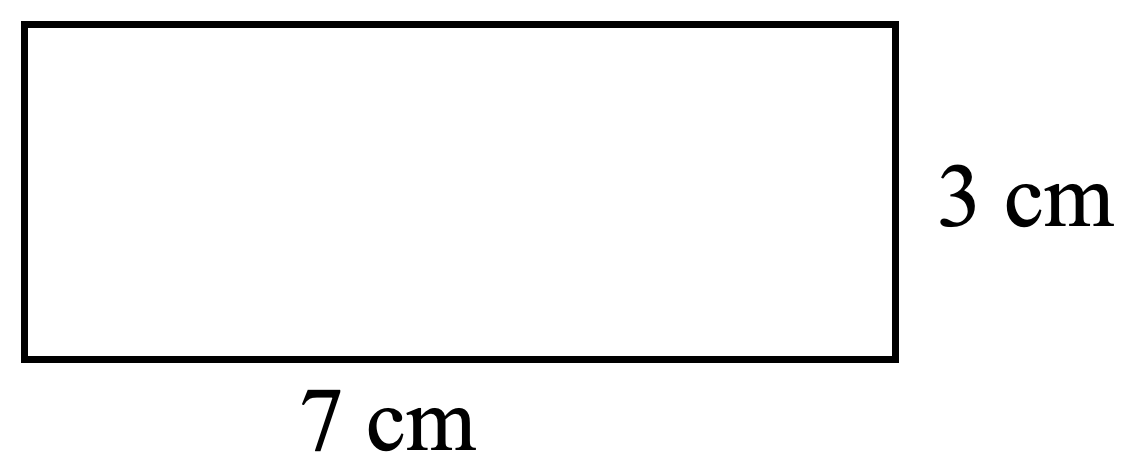
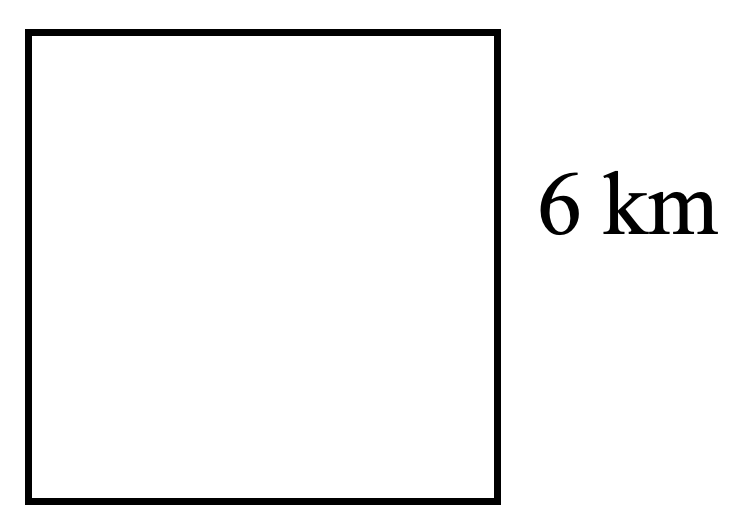
-
- A double-size bed cover measures 135 cm wide and 190 cm What is the perimeter and area of the bed cover?
- An Olympic size swimming is 50 m long and 25 m wide. What is the perimeter and area of the swimming pool?
Answers to Topic D Self-Test
-
- cm
- mm
- cm
- mm
- m or cm
- cm
- m
- km
-
- ii
- i
- ii
- ii
- iii
- i
-
- g
- kg
- mg
- g
-
Measure
Small Base Large volume milli Litre length milli metre kilo mass milli gram kilo -
- P = 20 cm, A = 21 cm2
- P = 24 km, A = 36 km2
- P = 392 m, A = 2208 m2
- P = 348 mm, A = 7569 mm2
- P = 650 cm, A = 25650 cm2
- P = 150 m, A = 1250 m2

