Chapter 11: Functions
11.7 Trigonometric Functions
Introductory trigonometry is based on identical the similarities between identical right angled (one angle is 90°) of different sizes. If the angles of a triangle are identical then all of this triangle is simply larger or smaller copies of each other.
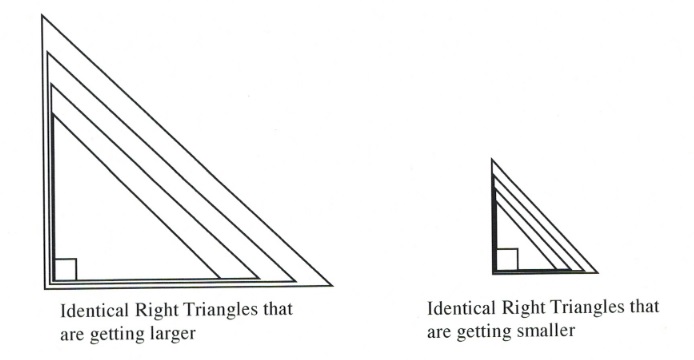
In all of the cases shown above if you take any two sides of any triangle shown and divide them by each other, that number will be exactly the same for the same two sides chosen from any of the triangles
These triangle ratios have defined names:
[latex]\text{sine}=\dfrac{\text{opposite}}{\text{hypotenuse}}\hspace{0.5in}\text{cosine}=\dfrac{\text{adjacent}}{\text{hypotenuse}}\hspace{0.5in}\text{tangent}=\dfrac{\text{opposite}}{\text{adjacent}}[/latex]
You often see these equations shortened to:
[latex]\text{sin}=\dfrac{\text{opp}}{\text{hyp}}\hspace{1in} \text{cos}=\dfrac{\text{adj}}{\text{hyp}}\hspace{1in}\text{tan}=\dfrac{\text{opp}}{\text{adj}}[/latex]
And memorized as:
[latex]\text{SOH}\hspace{1.2in} \text{CAH}\hspace{1.2in} \text{TOA}[/latex]
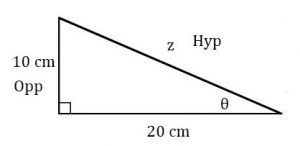
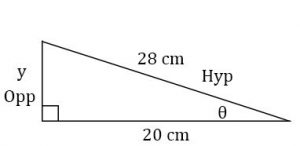
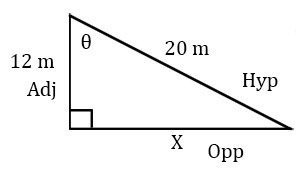
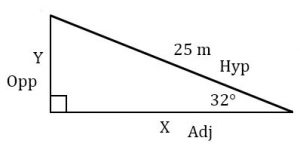
Defining the sides of a triangle follows a set pattern:
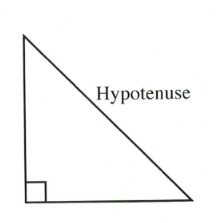 1st: The side of a triangle that is opposite to the right angle is called the hypotenuse.
1st: The side of a triangle that is opposite to the right angle is called the hypotenuse.
2nd: The opposite and adjacent sides are then defined by the angle you are going to work with. One of the sides will be opposite this angle and the other side will be beside (adjacent to) this side.
For example: The following sides are defined by the right angle and the angle you are going to work with Ø. You will have to define the adjacent and opposite sides for every right triangle you work with.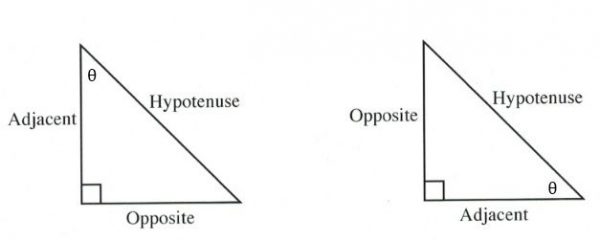
The other right-angled trigonometric rations are the reciprocals of sine, cosine and tangent:
[latex]\text{cosecant}=\dfrac{1}{\text{sine}}\hspace{0.25in} \text{secant}=\dfrac{1}{\text{cosine}}\hspace{0.25in} \text{cotangent}=\dfrac{1}{\text{tangent}}[/latex]
Or formally defined as:
[latex]\text{cosecant}=\dfrac{\text{hypotenuse}}{\text{opposite}}\hspace{0.25in} \text{secant}=\dfrac{\text{hypotenuse}}{\text{adjacent}}\hspace{0.25in} \text{cotangent}=\dfrac{\text{adjacent}}{\text{opposite}}[/latex]
You often see these equations shortened to:
[latex]\text{csc}=\dfrac{\text{hyp}}{\text{opp}}\hspace{0.75in} \text{sec}=\dfrac{\text{hyp}}{\text{adj}}\hspace{0.75in} \text{cot}=\dfrac{\text{adj}}{\text{opp}}[/latex]
These reciprocal trigonometric functions are commonly used in calculus, specifically in integration and when working with polar coordinates. Anyone taking higher levels of mathematics will encounter these reciprocal trigonometric functions.
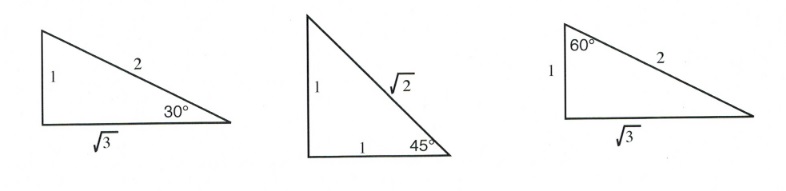
Using the Pythagorean theorem for 30°, 45° and 60° right angle triangles, you can get the exact values of the trigonometric relationship (and the reciprocal values). It is standard to see exams where students are required to draw these 30°, 45° and 60° right angle triangles and use the side lengths to generate exact values.
Standard Reference Angles
[latex]\begin{array}{lll} \text{sin }30^{\circ}=\dfrac{1}{2}\hspace{1in}&\text{sin }45^{\circ}=\dfrac{1}{\sqrt{2}}\hspace{1in}&\text{sin }60^{\circ}=\dfrac{\sqrt{3}}{2} \\ \\ \text{cos }30^{\circ}=\dfrac{\sqrt{3}}{2}\hspace{1in}&\text{cos }45^{\circ}=\dfrac{1}{\sqrt{2}}\hspace{1in}&\text{cos }60^{\circ}=\dfrac{1}{2} \\ \\ \text{tan }30^{\circ}=\dfrac{1}{\sqrt{3}}\hspace{1in}&\text{tan }45^{\circ}=1 \hspace{1in}&\text{tan }60^{\circ}=\sqrt{3} \end{array}[/latex]
Another common sight is to see trigonometric tables being used for approximations of the trig ratios of standard angles from 1° to 90°. For these tables, choose the value that lines up the trigonometric function you wish to use with the angle that you are using. Basic scientific calculators have essentially made these tables obsolete.
Example 11.7.1
Find the values that correspond to the following trigonometric functions and angles:
[latex]\text{sin } 19^{\circ} = X\hspace{0.5in} \text{cos } 67^{\circ} = Y\hspace{0.5in} \text{tan }38^{\circ}= Z[/latex]
Solution:
[latex]X = 0.326\hspace{0.5in} Y = 0.391\hspace{0.5in} Z = 0.781[/latex]
It is also possible to work in reverse—that is, given the trigonometric ration of two sides, you can find the angle that you are working with.
Example 11.7.2
Find the angles that correspond to the following trigonometric values:
[latex]\text{sin }{\theta}=0.829\hspace{0.5in} \text{cos }{\theta}=0.940\hspace{0.5in} \text{tan }{\theta}=3.732[/latex]
Solution:
[latex]{\theta} = 56^{\circ}\hspace{0.75in} {\theta} = 20^{\circ}\hspace{0.75in} {\theta} = 75^{\circ}[/latex]
Sometimes, you do not have a value that matches up. For these cases, you choose the value that is closest to what you have.
Example 11.7.3
Find the angles that are closest to the following trigonometric values:
[latex]\text{sin }{\theta}=0.297\hspace{0.5in} \text{cos }{\theta}=0.380\hspace{0.5in}\text{tan }{\theta}=0.635[/latex]
Solution:
[latex]{\theta} = 17^{\circ}\hspace{0.75in} {\theta} = 68^{\circ}\hspace{0.75in} {\theta} = 32^{\circ}[/latex]
Trigonometric Tables
[latex]\begin{array}{cllllcllll} \textbf{Angle}&\textbf{Sin}&\textbf{Cos}&\textbf{Tan}&\textbf{Csc}\hspace{0.5in}&\textbf{Angle}&\textbf{Sin}&\textbf{Cos}&\textbf{Tan}&\textbf{Csc} \\ 1& 0.017 &1.000 &0.017 &57.299 &46 &0.719 &0.695 &1.036 &1.390 \\ 2 &0.035& 0.999& 0.035 &28.654 &47 &0.731& 0.682 &1.072 &1.36 \\ 3& 0.052& 0.999 &0.052& 19.107 &48 &0.743 &0.669 &1.111 &1.346 \\ 4 &0.070 &0.998 &0.070 &14.336 &49 &0.755 &0.656 &1.150 &1.325 \\ 5& 0.087 &0.996 &0.087 &11.474 &50 &0.766 &0.643 &1.192 &1.305 \\ 6 &0.105 &0.995 &0.105 &9.567 &51 &0.777 &0.629 &1.235 &1.287 \\ 7& 0.122 &0.993 &0.123 &8.206 &52 &0.788 &0.616 &1.280 &1.269 \\ 8 &0.139 &0.990 &0.141 &7.185 &53 &0.799 &0.602 &1.327 &1.252 \\ 9 &0.156 &0.988 &0.158 &6.392 &54 &0.809 &0.588 &1.376 &1.236 \\ 10& 0.174 &0.985 &0.176 &5.759 &55 &0.819 &0.574 &1.428 &1.221 \\ 11& 0.191 &0.982 &0.194 &5.241 &56 &0.829 &0.559 &1.483 &1.206 \\ 12& 0.208 &0.978 &0.213 &4.810 &57 &0.839 &0.545 &1.540 &1.192 \\ 13& 0.225 &0.974 &0.231 &4.445 &58 &0.848 &0.530 &1.600 &1.179 \\ 14& 0.242 &0.970 &0.249 &4.134 &59 &0.857 &0.515 &1.664 &1.167 \\ 15& 0.259 &0.966 &0.268 &3.864 &60 &0.866 &0.500 &1.732 &1.155 \\ 16& 0.276 &0.961 &0.287 &3.628 &61 &0.875 &0.485 &1.804 &1.143 \\ 17 &0.292 &0.956 &0.306 &3.420 &62 &0.883 &0.469 &1.881 &1.133 \\ 18& 0.309 &0.951 &0.325 &3.236 &63 &0.891 &0.454 &1.963 &1.122 \\ 19& 0.326 &0.946 &0.344 &3.072 &64 &0.899 &0.438 &2.050 &1.113 \\ 20& 0.342 &0.940 &0.364 &2.924 &65 &0.906 &0.423 &2.145 &1.103 \\ 21& 0.358 &0.934 &0.384 &2.790 &66 &0.914 &0.407 &2.246 &1.095 \\ 22 &0.375 &0.927 &0.404 &2.669 &67 &0.921 &0.391 &2.356 &1.086 \\ 23 &0.391 &0.921 &0.424 &2.559 &68 &0.927 &0.375 &2.475 &1.079 \\ \end{array}[/latex]
[latex]\begin{array}{cllllcllll} \textbf{Angle}&\textbf{Sin}&\textbf{Cos}&\textbf{Tan}&\textbf{Csc}\hspace{0.5in}&\textbf{Angle}&\textbf{Sin}&\textbf{Cos}&\textbf{Tan}&\textbf{Csc} \\ 24 &0.407 &0.914 &0.445 &2.459 &69 &0.934 &0.358 &2.605 &1.071 \\ 25 &0.423 &0.906 &0.466 &2.366 &70 &0.940 &0.342 &2.747 &1.064 \\ 26& 0.438 &0.899 &0.488 &2.281 &71 &0.946 &0.326 &2.904 &1.058 \\ 27 &0.454 &0.891 &0.510 &2.203 &72 &0.951 &0.309 &3.078 &1.051 \\ 28 &0.469 &0.883 &0.532 &2.130 &73 &0.956 &0.292 &3.271 &1.046 \\ 29 &0.485 &0.875 &0.554 &2.063 &74 &0.961 &0.276 &3.487 &1.040 \\ 30 &0.500 &0.866 &0.577 &2.000 &75 &0.966 &0.259 &3.732 &1.035 \\ 31 &0.515 &0.857 &0.601 &1.942 &76 &0.970 &0.242 &4.011 &1.031 \\ 32 &0.530 &0.848 &0.625 &1.887 &77 &0.974 &0.225 &4.331 &1.026 \\ 33 &0.545 &0.839 &0.649 &1.836 &78 &0.978 &0.208 &4.705 &1.022 \\ 34 &0.559 &0.829 &0.675 &1.788 &79 &0.982 &0.191 &5.145 &1.019 \\ 35 &0.574 &0.819 &0.700 &1.743 &80 &0.985 &0.174 &5.671 &1.015 \\ 36 &0.588 &0.809 &0.727 &1.701 &81 &0.988 &0.156 &6.314 &1.012 \\ 37 &0.602 &0.799 &0.754 &1.662 &82 &0.990 &0.139 &7.115 &1.010 \\ 38& 0.616 &0.788 &0.781 &1.624 &83 &0.993 &0.122 &8.144 &1.008 \\ 39 &0.629 &0.777 &0.810 &1.589 &84 &0.995 &0.105 &9.514 &1.006 \\ 40 &0.643 &0.766 &0.839 &1.556 &85 &0.996 &0.087 &11.430 &1.004 \\ 41 &0.656 &0.755 &0.869 &1.524 &86 &0.998 &0.070 &14.301 &1.002 \\ 42 &0.669 &0.743 &0.900 &1.494 &87 &0.999 &0.052 &19.081 &1.001 \\ 43 &0.682 &0.731 &0.933 &1.466 &88 &0.999 &0.035 &28.636 &1.001 \\ 44 &0.695 &0.719 &0.966 &1.440 &89 &1.000 &0.017 &57.290& 1.000 \\ 45 &0.707 &0.707 &1.000 &1.414 &90 &1.000 &0.000 &&1.000 \end{array}[/latex]
Questions
Find the value of each of the following trigonometric functions to 6 digits using your scientific calculator.
- sin 48°
- sin 29°
- cos 25°
- cos 61°
- tan 11°
- tan 57°
- sin 11°
- cos 57°
Use your scientific calculator to find each angle to the nearest hundredth of a degree.
- sin θ = 0.4848
- sin θ = 0.6293
- cos θ = 0.6561
- cos θ = 0.6157
- tan θ = 0.6561
- tan θ = 0.1562
- sin θ = 0.6561
- cos θ = 0.1562
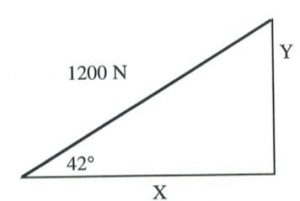
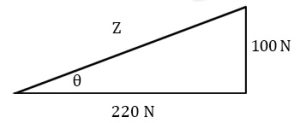
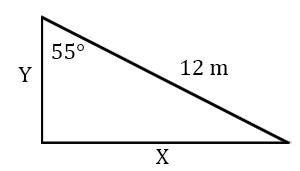
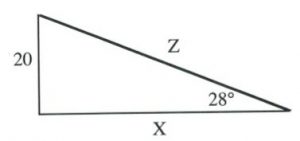
Solve for all unknowns in the following right triangles.