Unit 2: Adding and Subtracting Decimals
Topic A: Adding Decimals
Line Up the Decimals
Review place value in whole numbers and in decimal fractions.
Here is a place value chart for decimals:
| Hundreds | Tens | Ones | . | Tenths | Hundredths | Thousandths | Ten thousandths | Hundred thousandths |
|---|---|---|---|---|---|---|---|---|
| 3 | . | 4 | 5 | 3 | ||||
| 0 | . | 9 | 6 |
Vocabulary Review
Use the example below and the glossary to help you write the definitions.
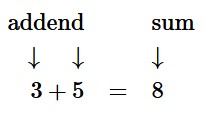
Definition of Addends:
Definition of Sum:
When adding decimals, you must be very careful to add together the digits with the same place value.
- Add thousandths to thousandths.
- Add hundredths to hundredths.
- Add tenths to tenths.
The best way to do this is to line up your decimals.
How to Add Decimals
- Write the addends underneath each other so the decimal points are in a straight column. Notice how lining up the decimals also lines up the place values.
[latex]0.43+0.2+0.804+0.1=[/latex]
Rewrite as: [latex]\begin{array}{ll}&0.43\\&0.2\\&0.804\\+&0.1\\ \hline\end{array}[/latex] - Put zeros at the end of the decimal fractions so that all fractions have the same number of decimal places.
[latex]\begin{array}{ll}&0.430\\&0.200\\&0.804\\+&0.100\\ \hline\end{array}[/latex] - It may help you to put the decimal point in the answer line before you do the addition.
[latex]\begin{array}{ll}&0.430\\&0.200\\&0.804\\+&0.100\\ \hline &\phantom{0}\mathbf{.}\end{array}[/latex] - When adding mixed decimals, be sure to keep the whole number places lined up as well. As you know, ones add to ones, tens to tens, hundreds to hundreds and so on. Put a decimal point after any whole numbers.
[latex]62.1 + 14.58 + 6. + 7.311 + 6.23 =\\ \begin{array}{lr}&62.100\\&14.580\\&6.000\\&7.311\\+&6.230 \\ \hline\end{array}[/latex] - Add each column, starting with the decimal place farthest to the right. If the total of a column is ten or more, carry the ten number to the next column as you are used to doing with whole numbers.
[latex]\begin{array}{ll}&\small{1\; 1}\\&0.470\\&0.298\\&0.100\\+&5.600\\ \hline &6.468\end{array}[/latex]
Exercise 1
Rewrite each question in columns and add.
- 0.24 + 0.73 + 0.51 =
[latex]\begin{array}{ll}&\scriptsize{1}\\&0.24\\&0.73\\+&0.51\\ \hline &1.48\end{array}[/latex] - 0.821 + 0.14 + 0.019 =
[latex]\begin{array}{ll}&\phantom{0.8}\scriptsize{1}\\&0.821\\&0.140\\+&0.019\\ \hline &0.980\end{array}[/latex]
- 0.084 + 0.291 + 0.652 =
- 0.195 + 0.982 + 0.605 =
- 0.625 + 0.845 + 0.33 =
- 0.442 + 0.782 + 0.254 =
Answers to Exercise 1
- 1.48
- 0.980
- 1.027
- 1.782
- 1.8
- 1.478
Exercise 2
Rewrite in columns and add.
- 1.003 + 141.2 + 0.47 =
[latex]\begin{array}{rr}&1.003\\&141.200\\+&0.470\\ \hline &142.673\end{array}[/latex] - 5.6 + 3.59 + 1829 =
[latex]\begin{array}{rr}&5.60\\&3.59\\+&1829.00\\ \hline &1838.19\end{array}[/latex]
- 4.6 + 2.59 + 1629 =
- 0.391 + 80 + 4.63 =
- 16.34 + 211.684 + 75.0697 =
- 321.6 + 485.791 + 0.001 =
- 0.22 + 46.84 + 95.6 =
- 0.042 + 0.018 + 19.1 =
Answers to Exercise 2
- 142.673
- 1838.19
- 1636.19
- 85.021
- 303.0937
- 807.392
- 142.66
- 19.16
Exercise 3
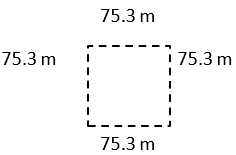
Find the perimeter of the squares described in each question. The measure of one side has been given. Draw a picture of each square to help visualize the question.
- S = 75.3 m
P = S + S + S + S
P = 75.3 + 75.3 + 75.3 + 75.3 m
P = 301.2 m
- S = 12.4 mm
P = - S = 100.73 km
P = - S = 50.2 cm
- S = 16.5 m
- S = 3.25 m
Answers to Exercise 3
- 301.2 m
- 49.6 mm
- 402.92 km
- 200.8 cm
- 66 m
- 13 m
Exercise 4
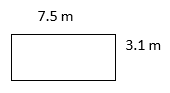
Find the perimeter of the rectangles described below. Draw your own rectangle if there is no picture.
- P = side + side + side + side
P =
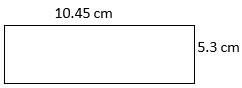
- P = side + side + side + side
P =
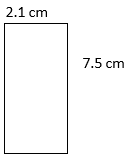
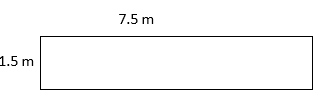
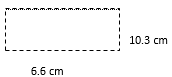
- l = 10.3 cm
w = 6.6 cm
- l = 100.03 km
w = 70.96 km - l = 9.75 cm
w = 3.5 cm
Answers to Exercise 4
- 21.2 m
- 31.5 cm
- 19.2 cm
- 18 m
- 33.8 cm
- 341.98 km
- 26.5 cm
Exercise 5
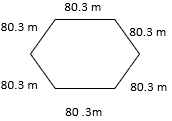
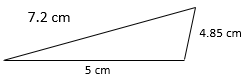
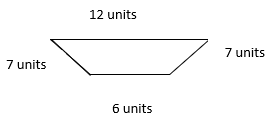
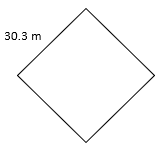
Find the perimeter of the polygons described below. Be sure the measurements are in the same unit value. Use a formula for each calculation, the formula work is started in the first two for you.
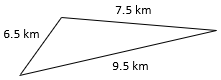
- P = Side + Side + Side
P = 6.5 km + 7.5 km + 9.5 km
P =
- P = Side + Side + Side + Side + Side + Side
P = + + + + +
P =
P =
- P =
- P =
- P =

- P =
Answers to Exercise 5
- 23.5 km
- 481.8 m
- 17.05 cm
- 32 units
- 20.78 km
- 121.2 m
How to Solve Word Problems
In math, word problems describe real-life situations that involve numbers.
Often the most difficult part of a word problem is knowing what we should do. Once we know what to do, it is much easier to figure out how to do it.
 It is sort of like driving. You may be all ready to go, but before you get into the car, turn on the engine, or put your foot on the gas pedal, you need to know where you are going and figure out how to get there.
It is sort of like driving. You may be all ready to go, but before you get into the car, turn on the engine, or put your foot on the gas pedal, you need to know where you are going and figure out how to get there.
The first thing to do is decide on your destination. 
Okay, how do you “decide on a destination” for a math problem?
Use these steps:
| Step 1: Question |
|
|---|---|
| Step 2: Information |
|
| Step 3: Operation |
|
| Step 4: Estimate |
|
| Step 5: Solve |
|
| Unit | Abbreviations |
|---|---|
| kilometre | km |
| metre | m |
| centimetre | cm |
| kilogram | kg |
| gram | g |
| litre | L |
Example A
The nutrition information on a box of cereal says that a regular serving contains 2.8 g of protein, 0.2 g of fat, 25 g of carbohydrate, and 1.9 g of “other nutrients.” Give the total number of grams in a regular serving.
| Step 1: Question | How many grams in a regular serving?
Draw a picture:
|
|---|---|
| Step 2: Information | What information is necessary to solve the problem?
|
| Step 3: Operation |
|
| Step 4: Estimate |
|
| Step 5: Solve | 2.8 g + 0.2 g + 25.0g + 1.9 g = 29.9 g
Answer: A regular serving of cereal is 29.9 grams ← (include the units)
|
Some key words that point to addition include:
Word Problems Using Addition of Decimals
Exercise 6
Use your skills in adding decimal fractions to do the following problems. Underline key words in the problems that will help you to recognize addition problems. Remember to draw a picture first!
- A road construction crew finished surfacing 5.7 km of highway one week and 4.4 km the next week. How many kilometres did they complete in that two weeks?
- 5.7 km + 4.4 km
- Estimation: 6 km + 4 km = 10 km
- Actual solution: [latex]\begin{array}[t]{rr}&5.7\text{ km}\\+&4.4\text{ km}\\ \hline &10.1\text{ km}\end{array}[/latex]
- Answer: The road crew completed 10.1 km of road surfacing in two weeks.
- Lisa rode her bike 4 km to her auntie’s house for a little visit. Then she rode 1.5 km to the grocery store to get apples and 0.7 km to Walmart to get bread and chips. From Walmart, she rode 3.6 km home. How far did she go on her bike altogether? (the picture has been drawn here but you will need to fill in the information)
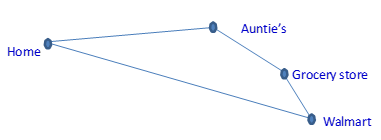
- Estimation:
- Actual solution:
- Answer:
- When Crystalle bought her used car, the odometer showed 12686.4 km. In one year, she drove 13294.8 km. What did the odometer read then? (draw your own picture)
- Estimation:
- Actual solution:
- Answer:
- A recipe for spaghetti sauce uses 1.25 kg of ground beef, 2.4 kg of fresh tomatoes, 1 kg of onions, 0.75 kg of celery, 0.5 kg of green pepper and lots of garlic and herbs. What is the total weight of the ingredients, not counting the garlic and herbs?
- Estimation:
- Actual solution:
- Answer:
- This month your power bill has increased $24.67, your phone bill has an extra $13.43, and your cable bill is up $2.24. It has been an expensive month! What is the combined extra cost that you are paying this month?
- Estimation:
- Actual solution:
- Answer:
- Wanda texted her boyfriend Curtis and asked him to pick up some groceries on the way home. He answered back “Only have $20. Is that enough?” Wanda wanted him to buy milk ($4.86), mac and cheese ($1.99), a bag of apples ($3.99) and laundry detergent ($8.57). Does Curtis have enough money?
- Estimation:
- Actual solution:
- Answer:
Answers to Exercise 6
- Estimation: 6 + 4 = 10
Actual solution: 5.7 + 4.4 = 10.1
Answer: The road crew completed 10.1 km of road surfacing in two weeks. - Estimation: 4 + 2 + 1 + 4 = 11
Actual solution: 4 + 1.5 + 0.7 + 3.6 = 9.8
Answer: Lisa rode her bike 9.8 km altogether. - Estimation: 13000 km + 13000 km = 26000 km
Actual solution: 12686.4 km + 13294.8 km = 25981.2 km
Answer: The odometer read 25 981.2 km after one year. - Estimation: 1 kg + 2 kg + 1 kg + 1 kg + 1 kg = 6 kg
Actual solution: 1.25 kg + 2.4 kg + 1 kg + 0.75 kg + 0.5 kg = 5.9 kg
Answer: The total weight of the ingredients is 5.9 kg. - Estimation: $25 + $13 + $2 = $40
Actual solution: $24.67 + $13.43 + $2.24 = $40.34
Answer: The extra cost you are paying is $40.34. - Estimation: $5 + $2 + $4 + 9 = $20
Actual solution: $4.86 + $1.99 + $3.99 + $8.57 = $19.41
Answer: The groceries will cost $19.41, so yes, Curtis has enough money.
Topic A: Self-Test
Mark /6 Aim 5/6
- Find the sum. (4 marks)
- [latex]\begin{array}{rr}&3.67\\&12.55\\&8.19\\+&5.67\\ \hline\\ \end{array}[/latex]
- [latex]5.27 + 2.4 + 8 + 6.93 + 10.27 =[/latex]
- [latex]\begin{array}{rr}&4.648\\&1.92\phantom{0}\\&1.275\\+&86.9\phantom{00}\\ \hline\\ \end{array}[/latex]
- [latex]2.72 + 0.6 + 110 + 17.223 =[/latex]
- Word Problem. (2 marks)
Gwen mailed Christmas presents to her family. She sent a 3.7 kg box to her daughter in Vancouver, a 2.145 kg package to her sister’s family in Campbell River, a box to Prince George that was 1.06 kg, and a parcel to Kitwanga that was 4 kg. What was the combined weight of Gwen’s parcels?- Estimate:
- Actual Solution:
- Answer:
Answers to Topic A Self-Test
- Find the sum.
- 30.08
- 32.87
- 94.743
- 130.543
- Word problem.
- Estimation: 4 kg + 2 kg +1 kg + 4 kg = 11 kg
- Actual Solution: 3.7 kg + 2.145 kg + 1.06 kg + 4 kg = 10.905 kg
- Answer: The combined weight of the parcels was 10.905 kg.
We understand numbers by the way the digits (numerals) are arranged in relationship to each other and to the decimal point. Each position has a certain value. Our number system is a decimal system. The place value is based on ten.
Any of the ten numerals (0 to 9) are digits. This term comes from our ten fingers which are called digits. The numerals came to be called "digits" from the practice of counting on the fingers!
The numbers to be added together in an addition question. In 3 + 5 = 8, the addends are 3 and 5.
A whole number and a decimal fraction. 1.75
The distance around the outside of a shape.
Make an approximate answer. Use the sign ≈ to mean approximately equal.
The result of an addition question, the answer to an addition question.
The amount altogether.



