Unit 1: Working with Decimals

Topic C: Comparing Decimals

More about Zeros…

A whole number can have a decimal point and many zeros after it without changing its value.

47 = 47.0 = 47.000 = 47.0000000000000000

Zeros are used to hold a place when we write whole numbers.

  • in 100, the 0s hold the tens place and the ones place
  • in 1206, the 0 holds the tens place

In decimals, any zero to the right of the decimal point and to the left of another digit is important because the zero is holding a place and giving the decimal the correct value.

  • in 4.306, the 0 holds the hundredths place
  • in 17.0002, the 0’s hold the tenth, hundredth and thousandth places.

A zero is usually placed to the left of the decimal point if there is no whole number.

0.5       0.937

Which Zeros are not Needed?

  • Zeros at the beginning, or far left, of whole numbers are not needed.
    • 00004 = 4
    • 00100 = 100
  • Zeros at the end, or far right, of decimal are not needed.
    • 3.210 = 3.21
    • 34.062000 = 34.062

Zeros on the outside edges of mixed decimals do not change the value of the number and are not necessary.

0028.9710 = 28.971

00100.003000 = 100.003

890.407 = 00890.4070000000

Exercise One

Cross out the zeros that are not needed.

  1. 70.0390
  2. 00.2906
  3. 06.30
  4. 087.50
  5. 60.0205
  6. 4 020.0020
  7. 400.080
  8. 340.600
  9. 03.5830
  10. 9.0
  11. 0.002030
  12. 50.300

Answers to Exercise One

  1. 709.039
  2. 0.2906
  3. 6.3
  4. 87.5
  5. 60.0205
  6. 4 020.002
  7. 400.08
  8. 340.6
  9. 3.583
  10. 9.0
  11. 0.00203
  12. 50.3

Zeros at the end of a decimal do not change the value.

6. = 6.0 = 6.00

And zeros at the beginning of a whole number do not change the value.

8 = 08 = 00008

But zeros between a decimal point and a digit do change the value.

Example A

405 is very different than 45. And 0.05 (five hundredths) is very different than 0.5 (five tenths).

Comparing Decimals

You have probably heard the old saying: “You cannot compare apples to oranges!” And it’s true, it is tough to compare things that do not have much in common. So before we compare decimals, we give the decimals something in common—the same number of decimal places which gives them a common understood denominator.

Before comparing decimals, put zeros at the end or cross out any unnecessary zeros so the decimals have a common (same) number of decimal places. If you write the decimals that you are comparing right underneath each other, your eye will often tell you which is the larger amount or if the amounts are equal.

Example B

Compare 0.43 and 0.4. Which is larger?

0.43 has two decimal places; it is forty-three hundredths  = [latex]\tfrac{43}{100}[/latex]. 0.4 has one decimal place; it is four tenths = [latex]\tfrac{4}{10}[/latex].

Give them a common number of decimal places.

Add a zero to 0.4 to make it 0.40; now we read it as forty hundredths = [latex]\tfrac{40}{100}[/latex].

Now, which is larger? [latex]\tfrac{40}{100} \text{ or }\tfrac{43}{100}[/latex].

You can easily see that 0.43 is the larger amount.

Review of Greater Than > and Less Than <

An easy way to remember these signs is to think that the big (wide) end of the sign is closer to the bigger (greater) number, and the small end of the sign is closer to the smaller number.

0.43 is larger than 0.40, 0.43 > 0.40

0.52 is smaller than 0.60, 0.52 < 0.60

Exercise Two

Which is greater? Draw a box around the bigger decimal fraction in each pair and write a greater than > or a less than < sign to make a true statement.

  1. 0.6   <    0.65
  2. 14   >    1.4
  3. 0.17          0.02
  4. 0.009         0.09
  5. 0.23         0.215
  6. 0.51         0.159
  7. 0.03         0.0352
  8. 0.07         0.063
  9. 630.3         630.03
  10. 0.80         0.6989

Answers to Exercise Two

  1. <
  2. >
  3. >
  4. <
  5. >
  6. >
  7. <
  8. >
  9. >
  10. >

Comparing Decimals Using a Number Line

You can compare decimals using a number line. A number line organizes what you are thinking about on paper – or on a ruler. You can plot your decimals on the number line and then be able to see which number is larger. Take a look:

Example C

First try to put the following numbers in order without looking at the number line below:

2.347     2.3          2.37        2.33        2.39        2.341       2.41

Then, look at the number line and see if you ordered your numbers correctly.  The number line has a jagged edge which means it does not start at zero.  It starts in the middle of a ruler. Using a number line can help you see your work and think about it at the same time.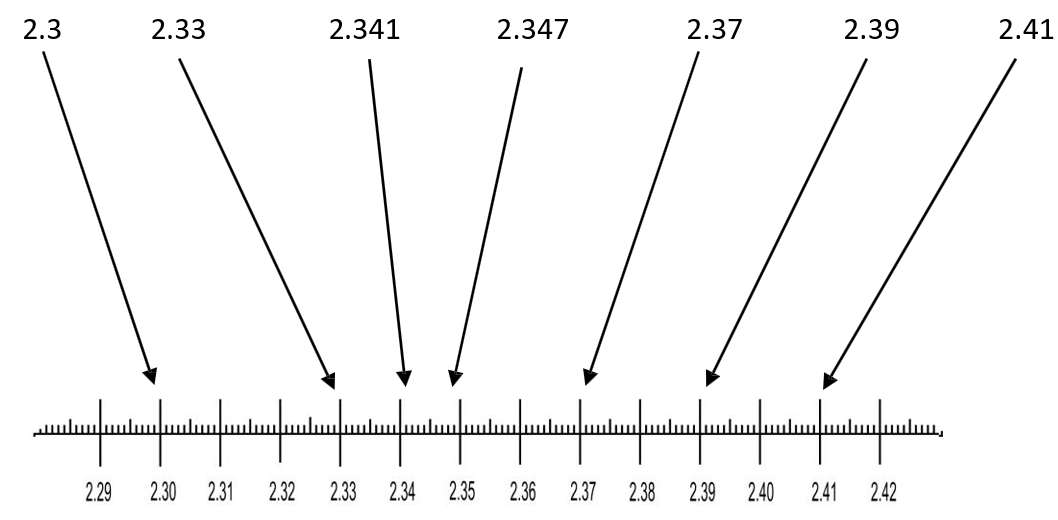A number line from 2.29 to 2.42. The numer line is labelled with the following numbers from right to left: 2.3, 2.33, 2.341, 2.347, 2.37, 2.39, 2.41.

Exercises

Try plotting the following decimals on the number line below:

4.59       4.32         4.7       5.23       4.47       4.3         4.17

 

a number line range from 4.0 to 5.0

Exercises

And now, plot these numbers on an empty number line. (You need to fill in the numbers yourself.  Plot 7.3 on the first large vertical line on the left)

7.35   7.3      8.2     7.53      7.98     8.34    7.9   7.5

An empty number line.

This is one way to organize and order decimals, please use it if the system is helpful for you.

Exercise Three

Draw a circle around the smallest decimal fraction in each group.

  1. 0.3,  0.03 ,  0.23
  2. 0.04  ,  0.14,  0.41
  3. 0.016,  0.2,  0.216
  4. 0.62,  0.6103,  0.5
  5. 0.041,  0.04,  0.4
  6. 100.1,  100.13,  100.01

Answers to Exercise Three

  1. 0.03
  2. 0.04
  3. 0.016
  4. 0.5
  5. 0.04
  6. 100.01

Exercise Four

Identify whether the pair of numbers is equal (=) or not equal (≠).

  1. 0.8    =    0.80
  2. 0.25    ≠     0.205
  3. 5.503          5.330
  4. 9.3200          9.32
  5. 0.75          0.750
  6. 23.3          2.33
  7. 0.040          0.40
  8. 0.8010          0.801

Answers to Exercise Four

  1. =
  2. ≠
  3. ≠
  4. =
  5. =
  6. ≠
  7. ≠
  8. =

Topic C: Self-Test

Mark /14      Aim 12/14

  1. Cross out the unnecessary zeros. (4 marks)
    1. 0401.02
    2. 1 000.001
    3. 68.3020
    4. 050.200
  2. Draw a box around the larger amount in each pair. (4 marks)
    1. 0.8 or  0.08
    2. 0.004 or  0.04
    3. 0.006 or  0.6
    4. 33.006 or  33.06
  3. Put the correct sign between the decimals.  Choose  =  or >  or <. (6 marks)
    1. 2.3          23
    2. 0.2          0.003
    3. 4.7          4.700
    4. 0.25          0.250
    5. 042.9002          042.9
    6. 0.4092          0.411

Answers to Topic C Self-Test

  1. Cross out the unnecessary zeros.
    1. 401.02
    2. 1 000.001
    3. 68.302
    4. 50.2
  2. Draw a box around the larger amount in each pair.
    1. 0.8
    2. 0.04
    3.  0.6
    4. 33.06
  3. Put the correct sign between the decimals.  Choose  =  or >  or <.
    1. <
    2. >
    3. =
    4. =
    5. >
    6. <
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Adult Literacy Fundamental Mathematics: Book 4 - 2nd Edition Copyright © 2023 by Katherine Arendt; Mercedes de la Nuez; and Liz Girard is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book