Unit 3: Multiplying Decimals

Topic A: Multiplying Decimals

Multiplying decimals uses the same method that you learned for multiplying whole numbers. Review multiplication of whole numbers.

Vocabulary Review

Review the diagram below and try to write in the explanations of the mathematical terms. You may refer to the glossary, if you wish. For right now, it is mostly important to remember what factor means.

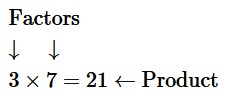
3 times 7 = 21. 3 and 7 are factors and 21 is the product.

Product:

Factors:

How to Multiply Decimals

Multiplying decimals follows almost the same steps as multiplying whole numbers. On the next few pages, you will be shown two ways to multiply decimals.

Method One

One method is to estimate the product using whole numbers to determine where the decimal goes.

Example A

[latex]4.3 × 5.7[/latex]

Estimate: 4.3 × 5.7 ≈ 4 × 6 = 24

This tells us that the correct answer will be around 24 (which is two whole number places). We know that the answer will not be around 2.4 and it will not be around 240.

If we take the decimals out and just multiply the digits, the answer is 2451.

[latex]\begin{array}{rr}&57\\ \times&43\\ \hline &171\\+&2280\\ \hline &2451\end{array}[/latex]

The estimate shows that the decimal point will come after two whole number places, so 4.3 × 5.7 = 24.51

[latex]\begin{array}{rr}&5.7\\ \times&4.3\\ \hline &171\\+&2280\\ \hline &24.51\end{array}[/latex]

Example B

[latex]23.24 × 3.9[/latex]

Estimate: 23.24 × 3.9 ≈ 23 × 4 = 92

The answer will be around 92. It will not be around 9.2 and it will not be around 920.

If we take the decimals out and just multiply the digits, the answer is 90636.

The estimate shows that the decimal point will come after two whole number places.

So [latex]23.24\times3.9 = 90.636[/latex]

[latex]\begin{array}{rr}&23.24\\ \times &3.9\\ \hline &20916\\+&69720\\ \hline &90.636\end{array}[/latex]

If the whole numbers in the question are large, you can round to the nearest ten or hundred to help you decide where to put the decimal point. This is a quick estimate.

Example C

[latex]383.298 × 213.87[/latex]

383.298 × 213.87 ≈ 400 × 200 = 80000

The answer will be around 80000.  It will not be around 8000 or 800000.

If we take the decimals out and just multiply the digits 383.298 by 213.87, the numerals in the product are 8197594326.

The estimate shows that the whole number will go up to the ten-thousands place, which is five whole number places, so

383.298 × 213.87 = 81975.94326   Whew!

[latex]\begin{array}{rr}&383.298\\ \times &213.87\\ \hline &81975.94326\end{array}[/latex]

Exercise 1

All the multiplying has been done already. Your task is to put the decimal point in the product by doing a whole number estimate of the question.

Example

[latex]\begin{array}{rr}&2.8\\ \times &4.3\\ \hline &84\\+&1120\\\hline&12.04\end{array}[/latex]     Estimate: [latex]\begin{array}{rr}&3\\ \times &4\\ \hline &12\end{array}[/latex]

  1. [latex]\begin{array}[t]{rr}&56.9\\ \times&12.3\\ \hline &1707\\ &11380\\&56900\\ \hline &69987\end{array}[/latex]
  2. [latex]\begin{array}[t]{rr}&7.3\\ \times&19.6\\ \hline &14308\end{array}[/latex]
  3. [latex]\begin{array}[t]{rrrr}&28.7\\ \times&64.97\\ \hline &1864639\end{array}[/latex]
  4. [latex]\begin{array}[t]{rrrr}&73.2\\ \times&1.6\\ \hline &11712\end{array}[/latex]
  5. [latex]\begin{array}[t]{rrrr}&1.8\\ \times&1.3\\ \hline &234\end{array}[/latex]
  6. [latex]\begin{array}[t]{rrrr}&48.29\\ \times&55.6\\ \hline&2684924\end{array}[/latex]
  7. [latex]\begin{array}[t]{rrrr}&91.2\\ \times&1.5\\ \hline&13680 \end{array}[/latex]

Answers to Exercise 1

  1. 699.87
  2. 143.08
  3. 1864.639
  4. 117.12
  5. 2.34
  6. 2684.924
  7. 136.80

Method Two

Another way of locating the decimal point in the product is to look at the number of decimal places in the decimals you are multiplying.

Example D

[latex]\begin{array}{lll}&43.23&\text{2 decimal places}\\ \times&19.6&\text{1 decimal place}\\ \hline \end{array}[/latex]

Then add the number of decimal places you counted above (2 + 1 = 3)

This is the number of decimal places you will have in your answer.

[latex]\begin{array}{lrl}&43.23&\text{2 decimal places}\\ \times&19.6&\text{1 decimal place}\\ \hline &847.\mathbf{308}&\text{3 decimal places}\end{array}[/latex]

Example E

[latex]\begin{array}{lrl}&0.35&\text{2 decimal places}\\ \times&0.47&\text{2 decimal places}\\ \hline &0.\mathbf{1645}&\text{4 decimal places}\end{array}[/latex]

Example F

[latex]\begin{array}{lrl}&13.452&\text{3 decimal places}\\ \times&30&\text{0 decimal places}\\ \hline &403.\mathbf{560}&\text{3 decimal places}\end{array}[/latex]

Exercise 2

Again, the multiplying has been done. Use the method of multiplying the understood denominators to put the decimal point in the product.

  1. [latex]\begin{array}{lrl}&9.2&\text{1 decimal place}\\ \times&0.3&\text{1 decimal place}\\ \hline &2.76&\text{2 decimal places}\end{array}[/latex]
  2. [latex]\begin{array}{lrl}&0.27&\text{2 decimal places}\\ \times&1.8&\text{1 decimal place}\\ \hline &0.486&\text{3 decimal places}\end{array}[/latex]
  3. [latex]\begin{array}{rr}&6.8\\ \times&0.4\\ \hline &272\end{array}[/latex]
  4. [latex]\begin{array}{rr}&2.4\\ \times &0.13\\ \hline &0312\end{array}[/latex]
  5. [latex]\begin{array}{rr}&240\\ \times &0.05\\ \hline &1200\end{array}[/latex]
  6. [latex]\begin{array}{rr}&0.91\\ \times&6.2\\ \hline &5642\end{array}[/latex]
  7. [latex]\begin{array}{rr}&0.29\\ \times&1.2\\ \hline &0348\end{array}[/latex]
  8. [latex]\begin{array}{rr}&0.87\\ \times&0.19\\ \hline &01653\end{array}[/latex]
  9. [latex]\begin{array}{rr}&7.3\\ \times &3.8\\ \hline & 2744\end{array}[/latex]
  10. [latex]\begin{array}{rr}&4.24\\ \times &0.07\\ \hline &02968\end{array}[/latex]
  11. [latex]\begin{array}{rr}&0.042\\ \times &60\\ \hline &2520\end{array}[/latex]

Answers to Exercise 2

  1. 2.76
  2. 0.486
  3. 2.72
  4. 0.312
  5. 12.00
  6. 5.642
  7. 0.348
  8. 0.1653
  9. 27.74
  10. 0.2968
  11. 2.52

Exercise 3

If you had trouble with the first two exercises, then get help from your instructor. Here is extra practice if you want or need it.

  1. [latex]\begin{array}{lrl}&41&\text{0 decimal places}\\ \times&0.061&\text{3 decimal places}\\ \hline &2.501&\text{3 decimal places}\end{array}[/latex]
  2. [latex]\begin{array}{lrl}&7.8&\text{1 decimal place}\\ \times&0.5&\text{1 decimal place}\\ \hline &3.90&\text{2 decimal places total}\end{array}[/latex]
  3. [latex]\begin{array}{rr}&59.275\\ \times&0.08\\ \hline &474200\end{array}[/latex]
  4. [latex]\begin{array}{rr}&7.18\\ \times &23.46\\ \hline &1684428\end{array}[/latex]
  5. [latex]\begin{array}{rr}&0.84\\ \times &2.1\\ \hline &1764\end{array}[/latex]
  6. [latex]\begin{array}{rr}&18.6\\ \times&0.3\\ \hline &558\end{array}[/latex]
  7. [latex]\begin{array}{rr}&100\\ \times&0.35\\ \hline &3500\end{array}[/latex]
  8. [latex]\begin{array}{rr}&0.72\\ \times&3.4\\ \hline &2448\end{array}[/latex]

Answers to Exercise 3

  1. 4.74200
  2. 168.4428
  3. 1.764
  4. 5.58
  5. 35.00
  6. 2.448

Exercise 4

Multiply to find the product. Remember to put the decimal point in the correct place; you know two methods!

  1. [latex]\begin{array}{lr}&13.8\\ \times&3.9\\ \hline &1242\\&4140\\ \hline &53.82\end{array}[/latex]
  2. [latex]\begin{array}{rrr}&0.076\\ \times&24\\ \hline \\ \end{array}[/latex]
  3. [latex]\begin{array}{rrr}&2.05\\ \times &1.7\\ \hline \\ \end{array}[/latex]
  4. [latex]\begin{array}{rrr}&0.429\\ \times &7.5\\ \hline \\ \end{array}[/latex]
  5. [latex]\begin{array}{rrr}&96\\ \times&0.2\\ \hline \\ \end{array}[/latex]
  6. [latex]\begin{array}{rrr}&1.79\\ \times&0.33\\ \hline \\ \end{array}[/latex]
  7. [latex]\begin{array}{rrr}&40.1\\ \times&0.9\\ \hline \\ \end{array}[/latex]

Answers to Exercise 4

  1. 53.82
  2. 1.824
  3. 3.485
  4. 3.2175
  5. 19.2
  6. 0.5907
  7. 36.09

Prefixing Zeros

Remember this skill?

  • [latex]\dfrac{23}{1000}=0.\mathbf{0}23[/latex] – The 0 must be used after the decimal point in 0.023 to hold the tenths place. This makes it clear that the denominator is one thousand.
  • [latex]\dfrac{7}{100}=0.\mathbf{0}7[/latex] – The 0 must be used after the decimal point in 0.07 to hold the tenths and hundredths place. This makes it clear that the denominator is one thousand.
  • [latex]\dfrac{8}{1000}=0.\mathbf{00}8[/latex] -The 00 must be used after the decimal point in 0.008 to hold the tenths and hundredths place. This makes it clear that the denominator is one thousand.

[latex]\dfrac{19}{10000}=0.\mathbf{00}19[/latex] – The 00 must be used after the decimal point in 0.0019 to hold the tenths and hundredths place. This makes it clear that the denominator is ten thousand.

When changing from a fraction to a decimal:

If there are not enough digits to fill all the decimal places, put zeros between the decimal point and the digits from the fraction—this is called prefixing zeros.

How does this apply to multiplying decimals? Look at the examples.

Example G

[latex]\begin{array}{lll}&0.07&\text{2 decimal places}\\ \times&0.5&\text{1 decimal place}\\ \hline &\phantom{0}35&\text{3 decimal places}\end{array}[/latex]

Uh oh! There are not enough spots in the answer to make the decimals fit in!

[latex]\begin{array}{rrc}&0.07\\ \times&0.5\\ \hline &\mathbf{00}35&\leftarrow\\&\small{3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]

Add zeros before your product. It is completely within the rules of math to do that. Then put in the decimal in the place in the correct place.

[latex]\begin{array}{rrc}&0.07\\ \times&0.5\\ \hline &\mathbf{0.0}35&\leftarrow\\&\small{3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]

Example H

[latex]\begin{array}{lrl}&0.07&\text{2 decimal places}\\ \times&0.03&\text{+2 decimal places}\\ \hline &.\underline{\;}\,\underline{\;}75&\text{4 decimal places in product}\\&\small{4\,3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]

Example I

Look carefully at this one – it is tricky!

[latex]\begin{array}{lrl}&0.05&\text{2 decimal places}\\ \times&0.8&\text{+1 decimal place}\\ \hline &.\underline{\;}75&\text{3 decimal places in product}\\&\small{3\, 2\, 1}&\small{\text{count}}\end{array}[/latex]

Because the last digit, the zero, is the result of multiplying 8 × 5, you must count it when working out the decimal places to put in the decimal point.

The product is forty thousandths:

[latex]\dfrac{40}{1000}=0.004[/latex]

which can now also be written as four hundredths:

[latex]\dfrac{40}{100}=0.04[/latex]

Note that if you had not counted that zero, you would have written 0.004 which is four thousandths and not correct.

Exercise 5

Find the products. Be certain to place all decimal points correctly.

  1. [latex]\begin{array}{rr}&0.35\\ \times&0.13\\ \hline&105\\&350\\ \hline & 0.0455\end{array}[/latex]
  2. [latex]\begin{array}{rr}&1.8\\ \times&0.05\\ \hline \\ \end{array}[/latex]
  3. [latex]\begin{array}{rr}&300\\ \times&0.04\\ \hline \\ \end{array}[/latex]
  4. [latex]\begin{array}{rr}&1.3\\ \times&0.027\\ \hline \\ \end{array}[/latex]
  5. [latex]\begin{array}{rr}&500\\ \times&0.073\\ \hline \\ \end{array}[/latex]
  6. [latex]\begin{array}{rr}&0.603\\ \times&0.4\\ \hline \\ \end{array}[/latex]
  7. [latex]\begin{array}{rr}&38.2\\ \times&1.9\\ \hline \\ \end{array}[/latex]
  8. [latex]\begin{array}{rr}&0.025\\ \times&0.25\\ \hline \\ \end{array}[/latex]
  9. [latex]\begin{array}{rr}&3.5\\ \times&0.018\\ \hline \\ \end{array}[/latex]
  10. [latex]\begin{array}{rr}&0.043\\ \times&3.3\\ \hline \\ \end{array}[/latex]
  11. [latex]\begin{array}{rr}&0.013\\ \times&1.4\\ \hline \\ \end{array}[/latex]
  12. [latex]\begin{array}{rr}&0.201\\ \times&2.1\\ \hline \\ \end{array}[/latex]

Answers to Exercise 5

  1. 0.0455
  2. 0.09
  3. 12.00
  4. 0.0351
  5. 36.500
  6. 0.2412
  7. 72.58
  8. 0.00625
  9. 0.063
  10. 0.1419
  11. 0.0182
  12. 0.4221

Multiplying by 10, 100, 1000, 10000…

There is a pattern that you can see when we multiply by a decimal number by 10, 100, 1000, 10000, and so on. Look at the following example and try to find the pattern:

45.9264 × 10 = 459.264

45.9264 × 100 = 4592.64

45.9264 × 1000 = 45926.4

45.9264 × 10000 = 459264

Do you see a pattern?

When multiplying by 10, 100, 1000, 10000, etc., count the zeros in the 10, 100, 1000, etc. and move the decimal point that same number of places to the right.

Multiply by Ten

When you multiply by ten, move the decimal point one place to the right. Remember that every whole number can have a decimal point at the right.

Example J

  1. .37 × 10 = 3.7
  2. 13 × 10 = 130

Exercise 6

  1. 2.2 × 10 =
  2. 6.67 × 10 =
  3. 2.1 × 100 =

Answers to Exercise 6

  1. 22
  2. 66.7
  3. 210

Multiply by 100

When you multiply by 100, move the decimal point two places to the right. Note that zeros may be needed at the end of the numeral.

Example K

  1. 4.2 × 100 = 420.
  2. 6 × 100 = 600.

Exercise 7

  1. 5.67 × 100 =
  2. 92.737 × 100 =
  3. 25 × 100 =

Answers:

  1. 567
  2. 9273.7
  3. 2500

Multiply by 1000

To multiply by 1000, move the decimal point three places to the right.

Example L

4.2 × 1000 = 4200.

Exercise 7

  1. 6.721 × 1000 =
  2. 1.56 × 1000 =
  3. 0.7246 × 1000 =
  4. 2.1 × 1000 =

Answers to Exercise 7

  1. 6721
  2. 1560
  3. 724.6
  4. 2100

Exercise 8

Write the products using the short method you now know.

  1. 0.4 × 10 =
  2. 0.27 × 10 =
  3. 10 × 0.926 =
  4. 10 × 0.09 =
  5. 0.62 ×100 =
  6. 0.119 × 100 =
  7. 100 × 2.03 =
  8. 100 × 0.345 =
  9. 1.934 × 1000 =
  10. 28.9 × 100 =

Answers to Exercise 8

  1. 4
  2. 2.7
  3. 9.26
  4. 0.9
  5. 62
  6. 11.9
  7. 203
  8. 34.5
  9. 1934
  10. 2890

Multiplying Decimals to Determine Area

The area of an object is: the measurement of the amount of space the object surface covers. Area is described in square units.

Exercise 9

Find the area of the rectangles described below. The measures of the length (l) and width (w) have been given. You should draw and label a sketch for each.

  1. l = 10.5 cm
    w = 6.6 cm

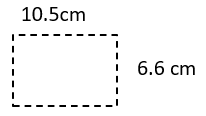
    A = l × w
    A = 10.5 × 6.6 cm
    A =
  2. l = 100.04 km
    w = 70.2 km
  3. l = 15.5 mm
    w = 10.5 mm
  4. l = 9.75 cm
    w = 3.5 cm
  5. l = 40.43 km
    w = 10.9 km
  6. l = 19.6 cm
    w = 2.8 cm

Answers to Exercise 9

  1. 69.3 cm2
  2. 7022.808 km2
  3. 162.75 mm2
  4. 34.125 cm2
  5. 440.687 km2
  6. 54.88 cm2

Exercise 10

Find the area of each square described in the questions below. Even though this is a simple square, it is still good practice to draw the picture.

Remember, all four sides of a square are the same length.

  1. A square, if  s = 5 cm
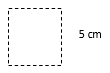
  2. A square, if  s = 12.5 km
  3. A square, if  s = 1.4 km
  4. A square, if  s = 25.4 cm

Answers to Exercise 10

  1. 25 cm2
  2. 156.25 km2
  3. 1.96 km2
  4. 645.16 cm2

Word Problems Using Multiplication of Decimals

Multiplication problems usually give information about one thing and ask you to find a total amount for several of the same things. Look for this pattern in the following problems. Also look for key words.

Some key words which point to multiplication include:

Multiplication by a decimal or fraction often uses the word “of” in word problems.

“Of” usually means multiply one number by another number.

Example M

Kathy spends 0.25 of her salary on rent. Her salary is $1445 a month. How much is her rent?

0.25 × $1445 = $361.25

She spends $361.25 on rent every month.

Remember, it can be very useful to draw a picture to help yourself visualize the problem.

Exercise 11

Solve these problems. Do an estimation first.

  1. One crate of juice costs $11.73. How much will five crates cost?
    • Estimation: $11.73  ≈  $12, 12 × 5 = 60
    • Actual Solution:
    • Answer:
  2. It takes Maria 0.75 hours to install a bathroom sink. The owner of the Ramada Hotel wants her to install 35 new sinks. How many hours of labour will Maria charge the hotel for this job?
    • Estimation:
    • Actual Solution:
    • Answer:
  3. Find the longest hallway in your learning centre. Stand at one end and count how many steps you take until you reach the other end. Write that number here.
    1. How many steps would you take if you walked down your hallway 4.5 times?
    2. How many steps would you take if you walked down your hallway 33.68 times?
  4. Jessica’s 4×4 truck averages 15.75 kilometres per litre of gas (km/L). How far could her truck travel with 52 L of gas?
    • Estimation:
    • Actual Solution:
    • Answer:
  5. The distance between Jackie’s work place and her home is 4.3 kilometres. She walks to work in the morning and then walks back to her home at the end of the work day, five days a week. How far does she walk each week?
    • Estimation:
    • Actual Solution:
    • Answer:
  6. A new subdivision is being built outside of Terrace. There are 21 new houses. Each house needs 25.2 metric tonnes of crushed rock for the driveway. How much crushed rock will be used to build all the driveways?
    • Estimation:
    • Actual Solution:
    • Answer:
  7. Union workers who work on statutory holidays are paid double time and a half. This is 2.5 times their regular pay.
    1. The employees at the coal terminal earn $17.37 per hour. How much are they paid per hour if they work on a statutory holiday?
    2. Jesse worked a 7.5 hour shift at the coal terminal on Labour Day last year. What were his earnings for that day?
  8. Lucy’s aunt in Hartley Bay has a large 50.5 m square vegetable garden. Lucy is going to help her aunt build a barbed wire fence to keep the deer out. The fence will be made with four strands of barbed wire. How much barbed wire should Lucy buy for her aunt? The fence will look like this:
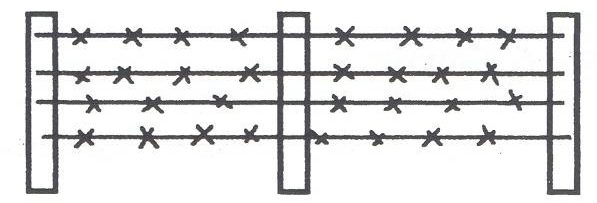
    Three fence posts and four lines of barbed wire stretched between the posts.
    • Draw a picture:
    • Estimation:
    • Actual Solution:
    • Answer:
  9. The directions on a carpet shampoo say one bottle will clean 50 m2 of carpet. Joyce wants to clean the wall-to-wall carpet in three rooms. The living room is 6 m by 4.5 m, the bedroom is 3 m by 4 m, and the hall is 1.2 m by 5 m. How many bottles of carpet shampoo should she buy? (This is a two-part question: Calculate the area of each of the rooms and then find the total area to be cleaned. Remember, Joyce cannot buy a partial bottle!)
    • Draw a picture:
    • Estimation:
    • Actual Solution:
    • Answer:

Answers to Exercise 11

  1. Estimation: $12 × 5 ≈ $60
    Actual Solution: $11.73 × 5 =  $58.65
    Five packages of juice will cost $58.65
  2. Estimation: 1 × 35 ≈ 35 hours
    Actual Solution: 0.75 × 35 = 26.25 hours
    It will take Maria 26.25 hours to install the sinks.
  3. Answers will vary. Please ask your instructor to check your work.
  4. Estimation: 16 km × 50 L ≈ 800 km
    Actual Solution: 15.75 km × 52 L = 819 km
    The truck could travel 819 km.
  5. Estimation: 4 × 10 km (5 trips there and 5 trips home) ≈ 44 seconds
    Actual Solution: 4.3km × 10 = 43 km
    Jackie walks 43 km each week.
  6. Estimation: 25 m × 20 m ≈ 500 m
    Actual Solution: 25.2 m × 21 = 529.2 m
    There will be 529.2 metric tonnes of crushed rock used for the driveways.
  7. Union workers:
    1. $17.37 × 2.5 = $43.425 per hour
    2. $43.425 × 7.5 hours = $325.69.
      Jesse earned $325.69 on Labour Day.
  8. Estimation: 50 + 50 + 50 + 50 ≈ 200 m, 200 m × 4 ≈ 800 m
    Actual Solution: 50.5m × 4 = 202m, 202 m × 4 = 808 m.
    Lucy should buy 808 m of barbed wire.
  9. Estimation: 
    6m × 5m ≈ 30m2
    3m × 4m ≈ 12m2
    1m × 5m ≈ 5m2
    30m2 + 12m2 + 5m2 ≈ 47m2
    Actual Solution: 
    6m × 4.5m = 27m2
    3m × 4m = 12m2
    1.2m × 5m = 6m2
    27m2 + 12m2 + 6m2 = 45m2
    Joyce should buy just one bottle of carpet cleaner.

Design Your Own House Project Part 2: Roofing Your House

Mark: /16

Use the graph paper house sketch that you made in the Design Your Own House Project Part 1 in Unit 2 – Topic B: Subtracting Decimals to do this activity.

  1. What is the area of your entire house? (area = length × width) /2
  2. The roof of a house overhangs (sticks out past) the edges of the house by 0.5 m. Add the overhang to the length and width of the house and find the area of the roof of your house. /2
  3. Before covering a roof, builders put down tarpaper, which keeps water out. Look at a hardware store flyer or go online and check prices for tarpaper. /1
    • Choose one type of tarpaper and write down the cost per roll.
  4. Use your answer for question a to figure out how many rolls will you need to cover the entire roof (remember, you cannot buy part of a roll). /2
  5. Using your answers for questions c and d, calculate what it would cost to cover the entire roof with tarpaper. /2
  6. Use a flyer or look at hardware stores online and choose a roofing material.  /1
    • Write down your choice.
  7. Roofing shingles are often sold in bundles that will cover 3 m2. Metal roofing materials are sold in sheets that will cover 50 square feet, which is the equivalent of 15 m2. What is the price per bundle or sheet for the material you chose in question f? /2
  8. Using your answer from question a, calculate how many bundles or sheets of roofing material you will need to cover your roof. /2
  9. Using your answers from questions g and h, calculate the total cost of roofing your house. /2

When you have finished this project, put your graph paper somewhere safe, because you will be using it again at the end of Unit 5 Topic A.

Marking Checklist for House Project Part 2

Calculations:

  • The area of the house has been calculated correctly.
  • The area of the roof has been calculated correctly.
  • The number of rolls of tarpaper has been calculated correctly.
  • The cost of covering the roof in tarpaper has been calculated correctly.
  • The number of bundles or sheets of roofing material has been calculated correctly.
  • The total cost of roofing the house has been calculated correctly.

Topic A: Self-Test

Mark /6          Aim 5/6

  1. Find the product. (4 marks)
    1. [latex]\begin{array}[t]{rr}&66\\ \times&0.7\\ \hline\\ \end{array}[/latex]
    2. [latex]\begin{array}[t]{rr}&7.25\\ \times&12\\ \hline\\ \end{array}[/latex]
    3. [latex]\begin{array}[t]{rr}&6.5\\ \times&0.6\\ \hline\\ \end{array}[/latex]
    4. [latex]\begin{array}[t]{rr}&19.5\\ \times&0.07\\ \hline\\ \end{array}[/latex]
  2. Problems. (2 marks)
    1. Rhonda bought a 3.4 kg roast at $2.89 per kilogram. What was the cost of her roast? (Round to the nearest cent.)
      • Estimation:
      • Actual Solution:

Answers for Topic A: Self Test

  1. Find the product.
    1. 46.2
    2. 87
    3. 3.9
    4. 1.365
  2. Problems.
    1. Estimate: 3 × 3 = $9
    2. Actual solution: 3.4 × 2.89 = 9.826 (round to nearest cent: $9.83). Rhonda paid $9.83 for her roast.
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Adult Literacy Fundamental Mathematics: Book 4 - 2nd Edition Copyright © 2023 by Katherine Arendt; Mercedes de la Nuez; and Liz Girard is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book