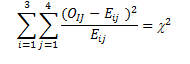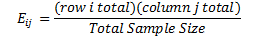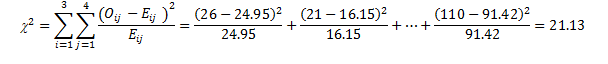Main Body
Chapter 4. Hypothesis Testing
Hypothesis testing is the other widely used form of inferential statistics. It is different from estimation because you start a hypothesis test with some idea of what the population is like and then test to see if the sample supports your idea. Though the mathematics of hypothesis testing is very much like the mathematics used in interval estimation, the inference being made is quite different. In estimation, you are answering the question, “What is the population like?” While in hypothesis testing you are answering the question, “Is the population like this or not?”
A hypothesis is essentially an idea about the population that you think might be true, but which you cannot prove to be true. While you usually have good reasons to think it is true, and you often hope that it is true, you need to show that the sample data support your idea. Hypothesis testing allows you to find out, in a formal manner, if the sample supports your idea about the population. Because the samples drawn from any population vary, you can never be positive of your finding, but by following generally accepted hypothesis testing procedures, you can limit the uncertainty of your results.
As you will learn in this chapter, you need to choose between two statements about the population. These two statements are the hypotheses. The first, known as the null hypothesis, is basically, “The population is like this.” It states, in formal terms, that the population is no different than usual. The second, known as the alternative hypothesis, is, “The population is like something else.” It states that the population is different than the usual, that something has happened to this population, and as a result it has a different mean, or different shape than the usual case. Between the two hypotheses, all possibilities must be covered. Remember that you are making an inference about a population from a sample. Keeping this inference in mind, you can informally translate the two hypotheses into “I am almost positive that the sample came from a population like this” and “I really doubt that the sample came from a population like this, so it probably came from a population that is like something else”. Notice that you are never entirely sure, even after you have chosen the hypothesis, which is best. Though the formal hypotheses are written as though you will choose with certainty between the one that is true and the one that is false, the informal translations of the hypotheses, with “almost positive” or “probably came”, is a better reflection of what you actually find.
Hypothesis testing has many applications in business, though few managers are aware that that is what they are doing. As you will see, hypothesis testing, though disguised, is used in quality control, marketing, and other business applications. Many decisions are made by thinking as though a hypothesis is being tested, even though the manager is not aware of it. Learning the formal details of hypothesis testing will help you make better decisions and better understand the decisions made by others.
The next section will give an overview of the hypothesis testing method by following along with a young decision-maker as he uses hypothesis testing. Additionally, with the provided interactive Excel template, you will learn how the results of the examples from this chapter can be adjusted for other circumstances. The final section will extend the concept of hypothesis testing to categorical data, where we test to see if two categorical variables are independent of each other. The rest of the chapter will present some specific applications of hypothesis tests as examples of the general method.
The strategy of hypothesis testing
Usually, when you use hypothesis testing, you have an idea that the world is a little bit surprising; that it is not exactly as conventional wisdom says it is. Occasionally, when you use hypothesis testing, you are hoping to confirm that the world is not surprising, that it is like conventional wisdom predicts. Keep in mind that in either case you are asking, “Is the world different from the usual, is it surprising?” Because the world is usually not surprising and because in statistics you are never 100 per cent sure about what a sample tells you about a population, you cannot say that your sample implies that the world is surprising unless you are almost positive that it does. The dull, unsurprising, usual case not only wins if there is a tie, it gets a big lead at the start. You cannot say that the world is surprising, that the population is unusual, unless the evidence is very strong. This means that when you arrange your tests, you have to do it in a manner that makes it difficult for the unusual, surprising world to win support.
The first step in the basic method of hypothesis testing is to decide what value some measure of the population would take if the world was unsurprising. Second, decide what the sampling distribution of some sample statistic would look like if the population measure had that unsurprising value. Third, compute that statistic from your sample and see if it could easily have come from the sampling distribution of that statistic if the population was unsurprising. Fourth, decide if the population your sample came from is surprising because your sample statistic could not easily have come from the sampling distribution generated from the unsurprising population.
That all sounds complicated, but it is really pretty simple. You have a sample and the mean, or some other statistic, from that sample. With conventional wisdom, the null hypothesis that the world is dull, and not surprising, tells you that your sample comes from a certain population. Combining the null hypothesis with what statisticians know tells you what sampling distribution your sample statistic comes from if the null hypothesis is true. If you are almost positive that the sample statistic came from that sampling distribution, the sample supports the null. If the sample statistic “probably came” from a sampling distribution generated by some other population, the sample supports the alternative hypothesis that the population is “like something else”.
Imagine that Thad Stoykov works in the marketing department of Pedal Pushers, a company that makes clothes for bicycle riders. Pedal Pushers has just completed a big advertising campaign in various bicycle and outdoor magazines, and Thad wants to know if the campaign has raised the recognition of the Pedal Pushers brand so that more than 30 per cent of the potential customers recognize it. One way to do this would be to take a sample of prospective customers and see if at least 30 per cent of those in the sample recognize the Pedal Pushers brand. However, what if the sample is small and just barely 30 per cent of the sample recognizes Pedal Pushers? Because there is variance among samples, such a sample could easily have come from a population in which less than 30 per cent recognize the brand. If the population actually had slightly less than 30 per cent recognition, the sampling distribution would include quite a few samples with sample proportions a little above 30 per cent, especially if the samples are small. In order to be comfortable that more than 30 per cent of the population recognizes Pedal Pushers, Thad will want to find that a bit more than 30 per cent of the sample does. How much more depends on the size of the sample, the variance within the sample, and how much chance he wants to take that he’ll conclude that the campaign did not work when it actually did.
Let us follow the formal hypothesis testing strategy along with Thad. First, he must explicitly describe the population his sample could come from in two different cases. The first case is the unsurprising case, the case where there is no difference between the population his sample came from and most other populations. This is the case where the ad campaign did not really make a difference, and it generates the null hypothesis. The second case is the surprising case when his sample comes from a population that is different from most others. This is where the ad campaign worked, and it generates the alternative hypothesis. The descriptions of these cases are written in a formal manner. The null hypothesis is usually called Ho. The alternative hypothesis is called either H1 or Ha. For Thad and the Pedal Pushers marketing department, the null hypothesis will be:
Ho: proportion of the population recognizing Pedal Pushers brand < .30
and the alternative will be:
Ha: proportion of the population recognizing Pedal Pushers brand >.30
Notice that Thad has stacked the deck against the campaign having worked by putting the value of the population proportion that means that the campaign was successful in the alternative hypothesis. Also notice that between Ho and Ha all possible values of the population proportion (>, =, and < .30) have been covered.
Second, Thad must create a rule for deciding between the two hypotheses. He must decide what statistic to compute from his sample and what sampling distribution that statistic would come from if the null hypothesis, Ho, is true. He also needs to divide the possible values of that statistic into usual and unusual ranges if the null is true. Thad’s decision rule will be that if his sample statistic has a usual value, one that could easily occur if Ho is true, then his sample could easily have come from a population like that which described Ho. If his sample’s statistic has a value that would be unusual if Ho is true, then the sample probably comes from a population like that described in Ha. Notice that the hypotheses and the inference are about the original population while the decision rule is about a sample statistic. The link between the population and the sample is the sampling distribution. Knowing the relative frequency of a sample statistic when the original population has a proportion with a known value is what allows Thad to decide what are usual and unusual values for the sample statistic.
The basic idea behind the decision rule is to decide, with the help of what statisticians know about sampling distributions, how far from the null hypothesis’ value for the population the sample value can be before you are uncomfortable deciding that the sample comes from a population like that hypothesized in the null. Though the hypotheses are written in terms of descriptive statistics about the population—means, proportions, or even a distribution of values—the decision rule is usually written in terms of one of the standardized sampling distributions—the t, the normal z, or another of the statistics whose distributions are in the tables at the back of statistics textbooks. It is the sampling distributions in these tables that are the link between the sample statistic and the population in the null hypothesis. If you learn to look at how the sample statistic is computed you will see that all of the different hypothesis tests are simply variations on a theme. If you insist on simply trying to memorize how each of the many different statistics is computed, you will not see that all of the hypothesis tests are conducted in a similar manner, and you will have to learn many different things rather than the variations of one thing.
Thad has taken enough statistics to know that the sampling distribution of sample proportions is normally distributed with a mean equal to the population proportion and a standard deviation that depends on the population proportion and the sample size. Because the distribution of sample proportions is normally distributed, he can look at the bottom line of a t-table and find out that only .05 of all samples will have a proportion more than 1.645 standard deviations above .30 if the null hypothesis is true. Thad decides that he is willing to take a 5 per cent chance that he will conclude that the campaign did not work when it actually did. He therefore decides to conclude that the sample comes from a population with a proportion greater than .30 that has heard of Pedal Pushers, if the sample’s proportion is more than 1.645 standard deviations above .30. After doing a little arithmetic (which you’ll learn how to do later in the chapter), Thad finds that his decision rule is to decide that the campaign was effective if the sample has a proportion greater than .375 that has heard of Pedal Pushers. Otherwise the sample could too easily have come from a population with a proportion equal to or less than .30.
| alpha | .1 | .05 | .03 | .01 |
|---|---|---|---|---|
| df infinity | 1.28 | 1.65 | 1.96 | 2.33 |
The final step is to compute the sample statistic and apply the decision rule. If the sample statistic falls in the usual range, the data support Ho, the world is probably unsurprising, and the campaign did not make any difference. If the sample statistic is outside the usual range, the data support Ha, the world is a little surprising, and the campaign affected how many people have heard of Pedal Pushers. When Thad finally looks at the sample data, he finds that .39 of the sample had heard of Pedal Pushers. The ad campaign was successful!
A straightforward example: testing for goodness-of-fit
There are many different types of hypothesis tests, including many that are used more often than the goodness-of-fit test. This test will be used to help introduce hypothesis testing because it gives a clear illustration of how the strategy of hypothesis testing is put to use, not because it is used frequently. Follow this example carefully, concentrating on matching the steps described in previous sections with the steps described in this section. The arithmetic is not that important right now.
We will go back to Chapter 1, where the Chargers’ equipment manager, Ann, at Camosun College, collected some data on the size of the Chargers players’ sport socks. Recall that she asked both the basketball and volleyball team managers to collect these data, shown in Table 4.2.
David, the marketing manager of the company that produces these socks, contacted Ann to tell her that he is planning to send out some samples to convince the Chargers players that wearing Easy Bounce socks will be more comfortable than wearing other socks. He needs to include an assortment of sizes in those packages and is trying to find out what sizes to include. The Production Department knows what mix of sizes they currently produce, and Ann has collected a sample of 97 basketball and volleyball players’ sock sizes. David needs to test to see if his sample supports the hypothesis that the collected sample from Camosun college players has the same distribution of sock sizes as the company is currently producing. In other words, is the distribution of Chargers players’ sock sizes a good fit to the distribution of sizes now being produced (see Table 4.2)?
| Size | Frequency | Relative Frequency |
|---|---|---|
| 6 | 3 | .031 |
| 7 | 24 | .247 |
| 8 | 33 | .340 |
| 9 | 20 | .206 |
| 10 | 17 | .175 |
From the Production Department, the current relative frequency distribution of Easy Bounce socks in production is shown in Table 4.3.
| Size | Relative Frequency |
|---|---|
| 6 | .06 |
| 7 | .13 |
| 8 | .22 |
| 9 | .3 |
| 10 | .26 |
| 11 | .03 |
If the world is unsurprising, the players will wear the socks sized in the same proportions as other athletes, so David writes his hypotheses:
Ho: Chargers players’ sock sizes are distributed just like current production.
Ha: Chargers players’ sock sizes are distributed differently.
Ann’s sample has n=97. By applying the relative frequencies in the current production mix, David can find out how many players would be expected to wear each size if the sample was perfectly representative of the distribution of sizes in current production. This would give him a description of what a sample from the population in the null hypothesis would be like. It would show what a sample that had a very good fit with the distribution of sizes in the population currently being produced would look like.
Statisticians know the sampling distribution of a statistic that compares the expected frequency of a sample with the actual, or observed, frequency. For a sample with c different classes (the sizes here), this statistic is distributed like χ2 with c-1 df. The χ2 is computed by the formula:
[latex]sample\;chi^2 = \sum{((O-E)^2)/E}[/latex]
where
O = observed frequency in the sample in this class
E = expected frequency in the sample in this class
The expected frequency, E, is found by multiplying the relative frequency of this class in the Ho hypothesized population by the sample size. This gives you the number in that class in the sample if the relative frequency distribution across the classes in the sample exactly matches the distribution in the population.
Notice that χ2 is always > 0 and equals 0 only if the observed is equal to the expected in each class. Look at the equation and make sure that you see that a larger value of χ2 goes with samples with large differences between the observed and expected frequencies.
David now needs to come up with a rule to decide if the data support Ho or Ha. He looks at the table and sees that for 5 df (there are 6 classes—there is an expected frequency for size 11 socks), only .05 of samples drawn from a given population will have a χ2 > 11.07 and only .10 will have a χ2 > 9.24. He decides that it would not be all that surprising if the players had a different distribution of sock sizes than the athletes who are currently buying Easy Bounce, since all of the players are women and many of the current customers are men. As a result, he uses the smaller .10 value of 9.24 for his decision rule. Now David must compute his sample χ2. He starts by finding the expected frequency of size 6 socks by multiplying the relative frequency of size 6 in the population being produced by 97, the sample size. He gets E = .06*97=5.82. He then finds O-E = 3-5.82 = -2.82, squares that, and divides by 5.82, eventually getting 1.37. He then realizes that he will have to do the same computation for the other five sizes, and quickly decides that a spreadsheet will make this much easier (see Table 4.4).
| Sock Size | Frequency in Sample | Population Relative Frequency | Expected Frequency = 97*C | (O-E)^2/E |
|---|---|---|---|---|
| 6 | 3 | .06 | 5.82 | 1.3663918 |
| 7 | 24 | .13 | 12.61 | 10.288033 |
| 8 | 33 | .22 | 21.34 | 6.3709278 |
| 9 | 20 | .3 | 29.1 | 2.8457045 |
| 10 | 17 | .26 | 25.22 | 2.6791594 |
| 11 | 0 | .03 | 2.91 | 2.91 |
| 97 | χ2 = 26.460217 |
David performs his third step, computing his sample statistic, using the spreadsheet. As you can see, his sample χ2 = 26.46, which is well into the unusual range that starts at 9.24 according to his decision rule. David has found that his sample data support the hypothesis that the distribution of sock sizes of the players is different from the distribution of sock sizes that are currently being manufactured. If David’s employer is going to market Easy Bounce socks to the BC college players, it is going to have to send out packages of samples that contain a different mix of sizes than it is currently making. If Easy Bounce socks are successfully marketed to the BC college players, the mix of sizes manufactured will have to be altered.
Now review what David has done to test to see if the data in his sample support the hypothesis that the world is unsurprising and that the players have the same distribution of sock sizes as the manufacturer is currently producing for other athletes. The essence of David’s test was to see if his sample χ2 could easily have come from the sampling distribution of χ2’s generated by taking samples from the population of socks currently being produced. Since his sample χ2 would be way out in the tail of that sampling distribution, he judged that his sample data supported the other hypothesis, that there is a difference between the Chargers players and the athletes who are currently buying Easy Bounce socks.
Formally, David first wrote null and alternative hypotheses, describing the population his sample comes from in two different cases. The first case is the null hypothesis; this occurs if the players wear socks of the same sizes in the same proportions as the company is currently producing. The second case is the alternative hypothesis; this occurs if the players wear different sizes. After he wrote his hypotheses, he found that there was a sampling distribution that statisticians knew about that would help him choose between them. This is the χ2 distribution. Looking at the formula for computing χ2 and consulting the tables, David decided that a sample χ2 value greater than 9.24 would be unusual if his null hypothesis was true. Finally, he computed his sample statistic and found that his χ2, at 26.46, was well above his cut-off value. David had found that the data in his sample supported the alternative χ2: that the distribution of the players’ sock sizes is different from the distribution that the company is currently manufacturing. Acting on this finding, David will include a different mix of sizes in the sample packages he sends to team coaches.
Testing population proportions
As you learned in Chapter 3, sample proportions can be used to compute a statistic that has a known sampling distribution. Reviewing, the z-statistic is:
[latex]z = (p-\pi)/\sqrt{\dfrac{(\pi)(1-\pi)}{n}}[/latex]
where
p = the proportion of the sample with a certain characteristic
π = the proportion of the population with that characteristic
[latex]\sqrt{\dfrac{(\pi)(1-\pi)}{n}}[/latex] = the standard deviation (error) of the proportion of the population with that characteristic
As long as the two technical conditions of π*n and (1-π)*n are held, these sample z-statistics are distributed normally so that by using the bottom line of the t-table, you can find what portion of all samples from a population with a given population proportion, π, have z-statistics within different ranges. If you look at the z-table, you can see that .95 of all samples from any population have z-statistics between ±1.96, for instance.
If you have a sample that you think is from a population containing a certain proportion, π, of members with some characteristic, you can test to see if the data in your sample support what you think. The basic strategy is the same as that explained earlier in this chapter and followed in the goodness-of-fit example: (a) write two hypotheses, (b) find a sample statistic and sampling distribution that will let you develop a decision rule for choosing between the two hypotheses, and (c) compute your sample statistic and choose the hypothesis supported by the data.
Foothill Hosiery recently received an order for children’s socks decorated with embroidered patches of cartoon characters. Foothill did not have the right machinery to sew on the embroidered patches and contracted out the sewing. While the order was filled and Foothill made a profit on it, the sewing contractor’s price seemed high, and Foothill had to keep pressure on the contractor to deliver the socks by the date agreed upon. Foothill’s CEO, John McGrath, has explored buying the machinery necessary to allow Foothill to sew patches on socks themselves. He has discovered that if more than a quarter of the children’s socks they make are ordered with patches, the machinery will be a sound investment. John asks Kevin to find out if more than 35 per cent of children’s socks are being sold with patches.
Kevin calls the major trade organizations for the hosiery, embroidery, and children’s clothes industries, and no one can answer his question. Kevin decides it must be time to take a sample and test to see if more than 35 per cent of children’s socks are decorated with patches. He calls the sales manager at Foothill, and she agrees to ask her salespeople to look at store displays of children’s socks, counting how many pairs are displayed and how many of those are decorated with patches. Two weeks later, Kevin gets a memo from the sales manager, telling him that of the 2,483 pairs of children’s socks on display at stores where the salespeople counted, 826 pairs had embroidered patches.
Kevin writes his hypotheses, remembering that Foothill will be making a decision about spending a fair amount of money based on what he finds. To be more certain that he is right if he recommends that the money be spent, Kevin writes his hypotheses so that the unusual world would be the one where more than 35 per cent of children’s socks are decorated:
Ho: π decorated socks < .35
Ha: π decorated socks > .35
When writing his hypotheses, Kevin knows that if his sample has a proportion of decorated socks well below .35, he will want to recommend against buying the machinery. He only wants to say the data support the alternative if the sample proportion is well above .35. To include the low values in the null hypothesis and only the high values in the alternative, he uses a one-tail test, judging that the data support the alternative only if his z-score is in the upper tail. He will conclude that the machinery should be bought only if his z-statistic is too large to have easily come from the sampling distribution drawn from a population with a proportion of .35. Kevin will accept Ha only if his z is large and positive.
Checking the bottom line of the t-table, Kevin sees that .95 of all z-scores associated with the proportion are less than -1.645. His rule is therefore to conclude that his sample data support the null hypothesis that 35 per cent or less of children’s socks are decorated if his sample (calculated) z is less than -1.645. If his sample z is greater than -1.645, he will conclude that more than 35 per cent of children’s socks are decorated and that Foothill Hosiery should invest in the machinery needed to sew embroidered patches on socks.
Using the data the salespeople collected, Kevin finds the proportion of the sample that is decorated:
[latex]\pi = 826/2483 = .333[/latex]
Using this value, he computes his sample z-statistic:
[latex]z = (p-\pi)/(\sqrt{\dfrac{(\pi)(1-\pi)}{n}}) = (.333-.35)/(\sqrt{\dfrac{(.35)(1-.35)}{2483}}) = \dfrac{-.0173}{.0096} = -1.0811[/latex]
All these calculations, along with the plots of both sampling distribution of π and the associated standard normal distributions, are computed by the interactive Excel template in Figure 4.1.
Figure 4.1 Interactive Excel Template for Test of Hypothesis – see Appendix 4.
Kevin’s collected numbers, shown in the yellow cells of Figure 4.1., can be changed to other numbers of your choice to see how the business decision may be changed under alternative circumstances.
Because his sample (calculated) z-score is larger than -1.645, it is unlikely that his sample z came from the sampling distribution of z’s drawn from a population where π < .35, so it is unlikely that his sample comes from a population with π < .35. Kevin can tell John McGrath that the sample the salespeople collected supports the conclusion that more than 35 per cent of children’s socks are decorated with embroidered patches. John can feel comfortable making the decision to buy the embroidery and sewing machinery.
Testing independence and categorical variables
We also use hypothesis testing when we deal with categorical variables. Categorical variables are associated with categorical data. For instance, gender is a categorical variable as it can be classified into two or more categories. In business, and predominantly in marketing, we want to determine on which factor(s) customers base their preference for one type of product over others. Since customers’ preferences are not the same even in a specific geographical area, marketing strategists and managers are often keen to know the association among those variables that affect shoppers’ choices. In other words, they want to know whether customers’ decisions are statistically independent of a hypothesized factor such as age.
For example, imagine that the owner of a newly established family restaurant in Burnaby, BC, with branches in North Vancouver, Langley, and Kelowna, is interested in determining whether the age of the restaurant’s customers affects which dishes they order. If it does, she will explore the idea of charging different prices for dishes popular with different age groups. The sales manager has collected data on 711 sales of different dishes over the last six months, along with the approximate age of the customers, and divided the customers into three categories. Table 4.5 shows the breakdown of orders and age groups.
| Orders | ||||||
| Fish | Veggie | Steak | Spaghetti | Total | ||
| Age Groups | Kids | 26 | 21 | 15 | 20 | 82 |
| Adults | 100 | 74 | 60 | 70 | 304 | |
| Seniors | 90 | 45 | 80 | 110 | 325 | |
| Total | 216 | 140 | 155 | 200 | 711 | |
The owner writes her hypotheses:
Ho: Customers’ preferences for dishes are independent of their ages
Ha: Customers’ preferences for dishes depend on their ages
The underlying test for this contingency table is known as the chi-square test. This will determine if customers’ ages and preferences are independent of each other.
We compute both the observed and expected frequencies as we did in the earlier example involving sports socks where O = observed frequency in the sample in each class, and E = expected frequency in the sample in each class. Then we calculate the expected frequency for the above table with i rows and j columns, using the following formula:
This chi-square distribution will have (i-1)(j-1) degrees of freedom. One technical condition for this test is that the value for each of the cells must not be less than 5. Figure 4.2 provides the hypothesized values for different levels of significance.
The expected frequency, Eij, is found by multiplying the relative frequency of each row and column, and then dividing this amount by the total sample size. Thus,
For each of the expected frequencies, we select the associated total row from each of the age groups, and multiply it by the total of the same column, then divide it by the total sample size. For the first row and column, we multiply (82 *216)/711=24.95. Table 4.6 summarizes all expected frequencies for this example.
| Orders | ||||||
|---|---|---|---|---|---|---|
| Fish | Veggie | Steak | Spaghetti | Total | ||
| Age Groups | Kids | 24.95 | 16.15 | 17.88 | 23.07 | 82 |
| Adults | 92.35 | 59.86 | 66.27 | 85.51 | 304 | |
| Seniors | 98.73 | 63.99 | 70.85 | 91.42 | 325 | |
| Total | 216 | 140 | 155 | 200 | 711 | |
Now we use the calculated expected frequencies and the observed frequencies to compute the chi-square test statistic:
We computed the sample test statistic as 21.13, which is above the 12.592 cut-off value of the chi-square table associated with (3-1)*(4-1) = 6 df at .05 level. To find out the exact cut-off point from the chi-square table, you can enter the alpha level of .05 and the degrees of freedom, 6, directly into the yellow cells in the following interactive Excel template (Figure 4.2). This template contains two sheets; it will plot the chi-square distribution for this example and will automatically show the exact cut-off point.
Figure 4.2 Interactive Excel Template for Determining Chi-Square Cut-off Point – see Appendix 4.
The result indicates that our sample data supported the alternative hypothesis. In other words, customers’ preferences for different dishes depended on their age groups. Based on this outcome, the owner may differentiate price based on these different age groups.
Using the test of independence, the owner may also go further to find out if such dependency exists among any other pairs of categorical data. This time, she may want to collect data for the selected age groups at different locations of her restaurant in British Columbia. The results of this test will reveal more information about the types of customers these restaurants attract at different locations. Depending on the availability of data, such statistical analysis can also be carried out to help determine an improved pricing policy for different groups in different locations, at different times of day, or on different days of the week. Finally, the owner may also redo this analysis by including other characteristics of these customers, such as education, gender, etc., and their choice of dishes.
Summary
This chapter has been an introduction to hypothesis testing. You should be able to see the relationship between the mathematics and strategies of hypothesis testing and the mathematics and strategies of interval estimation. When making an interval estimate, you construct an interval around your sample statistic based on a known sampling distribution. When testing a hypothesis, you construct an interval around a hypothesized population parameter, using a known sampling distribution to determine the width of that interval. You then see if your sample statistic falls within that interval to decide if your sample probably came from a population with that hypothesized population parameter. Hypothesis testing also has implications for decision-making in marketing, as we saw when we extended our discussion to include the test of independence for categorical data.
Hypothesis testing is a widely used statistical technique. It forces you to think ahead about what you might find. By forcing you to think ahead, it often helps with decision-making by forcing you to think about what goes into your decision. All of statistics requires clear thinking, and clear thinking generally makes better decisions. Hypothesis testing requires very clear thinking and often leads to better decision-making.