Chapter 6. Gases
34 Kinetic Molecular Theory of Gases
Jessie A. Key and David W. Ball
Learning Objectives
- State the major concepts behind the kinetic molecular theory of gases.
- Demonstrate the relationship between kinetic energy and molecular speed.
- Apply the kinetic molecular theory to explain and predict the gas laws.
Gases were among the first substances studied using the modern scientific method, which was developed in the 1600s. It did not take long to recognize that gases all shared certain physical behaviours, suggesting that gases could be described by one all-encompassing theory. The kinetic molecular theory of gases is a model that helps us understand the physical properties of gases at the molecular level. It is based on the following concepts:
- Gases consist of particles (molecules or atoms) that are in constant random motion.
- Gas particles are constantly colliding with each other and the walls of their container. These collisions are elastic; that is, there is no net loss of energy from the collisions.
- Gas particles are small and the total volume occupied by gas molecules is negligible relative to the total volume of their container.
- There are no interactive forces (i.e., attraction or repulsion) between the particles of a gas.
- The average kinetic energy of gas particles is proportional to the absolute temperature of the gas, and all gases at the same temperature have the same average kinetic energy.
Figure 6.6 “The Kinetic Molecular Theory of Gases” shows a representation of how we mentally picture the gas phase.

Because most of the volume occupied by a gas is empty space, a gas has a low density and can expand or contract under the appropriate influence. The fact that gas particles are in constant motion means that two or more gases will always mix as the particles from the individual gases move and collide with each other. The number of collisions the gas particles make with the walls of their container and the force with which they collide determine the magnitude of the gas pressure.
Kinetic Energy and Molecular Speed
Gas particles are in constant motion, and any object in motion has kinetic energy (Ek). Kinetic energy, for an individual atom, can be calculated by the following equation where m is the mass, and u is the speed.
![]()
Overall, the molecules in a sample of a gas share an average kinetic energy; however, individual molecules exhibit a distribution of kinetic energies because of having a distribution of speeds (Figure 6.7 “Stylized Molecular Speed Distribution”). This distribution of speeds arises from the collisions that occur between molecules in the gas phase. Although these collisions are elastic (there is no net loss of energy), the individual speeds of each molecule involved in the collision may change. For example, in the collision of two molecules, one molecule may be deflected at a slightly higher speed and the other at a slightly lower speed, but the average kinetic energy does not change.
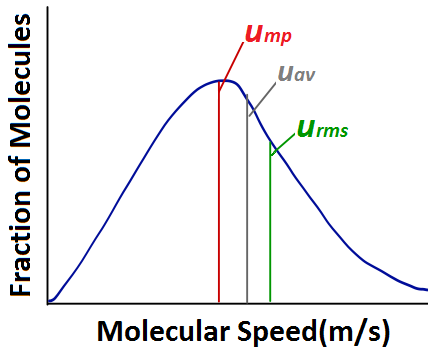
When analyzing a diagram of the distribution of molecular speeds, there are several commonly used terms to be familiar with. The most probable speed (ump) is the speed of the largest number of molecules, and corresponds to the peak of the distribution. The average speed (uav) is the mean speed of all gas molecules in the sample. The root-mean-square (rms) speed (urms) corresponds to the speed of molecules having exactly the same kinetic energy as the average kinetic energy of the sample.
According to the kinetic molecular theory, the average kinetic energy of gas particles is proportional to the absolute temperature of the gas. This can be expressed with the following equation where k represents the Boltzmann constant. The Boltzmann constant is simply the gas constant R divided by the Avogadro’s constant (NA). The bar above certain terms indicates they are average values.
![]()
Since average kinetic energy is related both to the absolute temperature and the molecular speed, we can combine the equation above with the previous one to determine the rms speed.
![]()
![]()
![]()
This demonstrates that the rms speed is related to the temperature. We can further manipulate this equation by multiplying the numerator and denominator by Avogadro’s constant (NA) to give us a form using the gas constant (R) and molar mass (M).
![]()
This form of the equation demonstrates that the rms speed of gas molecules is also related to the molar mass of the substance. Comparing two gases of different molar mass at the same temperature, we see that despite having the same average kinetic energy, the gas with the smaller molar mass will have a higher rms speed.
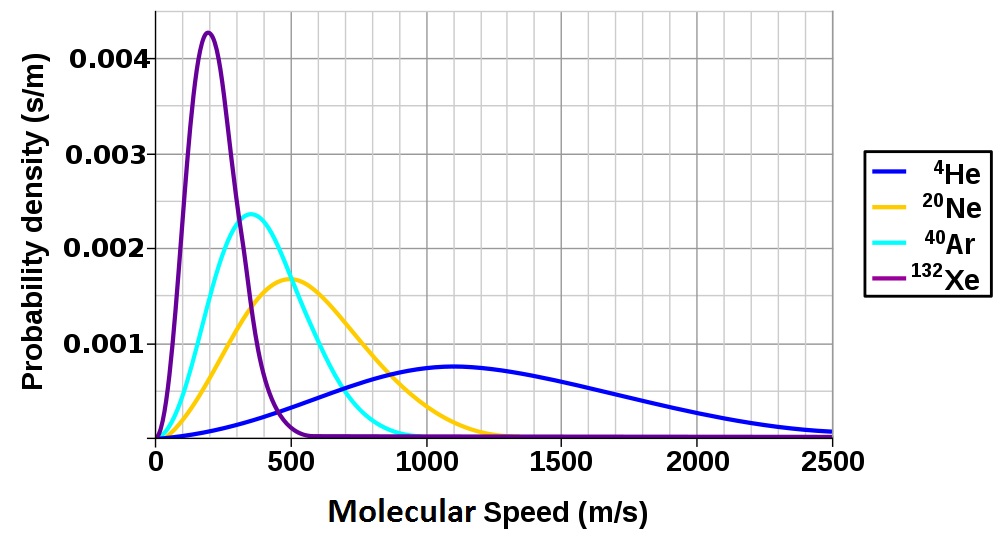
Figure 6.9 Molecular Speed Distribution of Noble Gases[1]
Example 6.19
Problem
Calculate the rms speed of nitrogen molecules at 25ºC.
Solution
Calculate the rms speed of nitrogen molecules at 25ºC.Solution
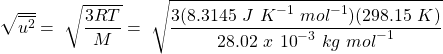
![]()
Knowing that 1 J = 1 kg m2 s-2 we can convert to metres per second:
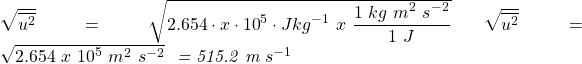
Applying the Kinetic Molecular Theory to the Gas Laws
The kinetic molecular theory can be used to explain or predict the experimental trends that were used to generate the gas laws. Let’s work through a few scenarios to demonstrate this point.
What will happen to the pressure of a system where the volume is decreased at constant temperature?
This problem can be approached in two ways:
1. The ideal gas law can be rearranged to solve for pressure and estimate the change in pressure:
![]()
![]()
Volume is located in the denominator of the equation, and it is being decreased. This means the rest of the equation is being divided by a smaller number, so that should make the pressure larger.
2. The kinetic molecular theory can be used. Since the temperature is remaining constant, the average kinetic energy and the rms speed remain the same as well. The volume of the container has decreased, which means that the gas molecules have to move a shorter distance to have a collision. There will therefore be more collisions per second, causing an increase in pressure.
What will happen to the pressure of a system where the temperature is increased and the volume remains constant?
Again, this type of problem can be approached in two ways:
1. The ideal gas law can be rearranged to solve for pressure and estimate the change in pressure.
![]()
Temperature is located in the numerator; there is a direct relationship between temperature and pressure. Therefore an increase in temperature should cause an increase in pressure.
2. The kinetic molecular theory can be used. Temperature is increased, so the average kinetic energy and the rms speed should also increase. This means that the gas molecules will hit the container walls more frequently and with greater force because they are all moving faster. This should increase the pressure.
Key Takeaways
- The physical behaviour of gases is explained by the kinetic molecular theory of gases.
- The number of collisions that gas particles make with the walls of their container and the force at which they collide determine the magnitude of the gas pressure.
- Temperature is proportional to average kinetic energy.
Exercises
Questions
- State the ideas of the kinetic molecular theory of gases.
- Calculate the rms speed of CO2at 40°C.
- Using the kinetic molecular theory, explain how an increase in the number of moles of gas at constant volume and temperature affects the pressure.
Answers
- Gases consist of tiny particles of matter that are in constant motion. Gas particles are constantly colliding with each other and the walls of a container. These collisions are elastic; that is, there is no net loss of energy from the collisions. Gas particles are separated by large distances. The size of gas particles is tiny compared to the distances that separate them and the volume of the container. There are no interactive forces (i.e., attraction or repulsion) between the particles of a gas. The average kinetic energy of gas particles is dependent on the temperature of the gas.
- 421 m/s
- Temperature remains the same, so the average kinetic energy and the rms speed should remain the same. Increasing the number of moles of gas means there are more molecules of gas available to collide with the walls of the container at any given time. Therefore pressure should increase.
Media Attributions
- “The Kinetic Molecular Theory of Gases” by David W. Ball © CC BY-NC-SA (Attribution NonCommercial ShareAlike)
- “Stylized Molecular Speed Distribution” by David W. Ball and Jessie A. Key © CC BY-NC-SA (Attribution NonCommercial ShareAlike)
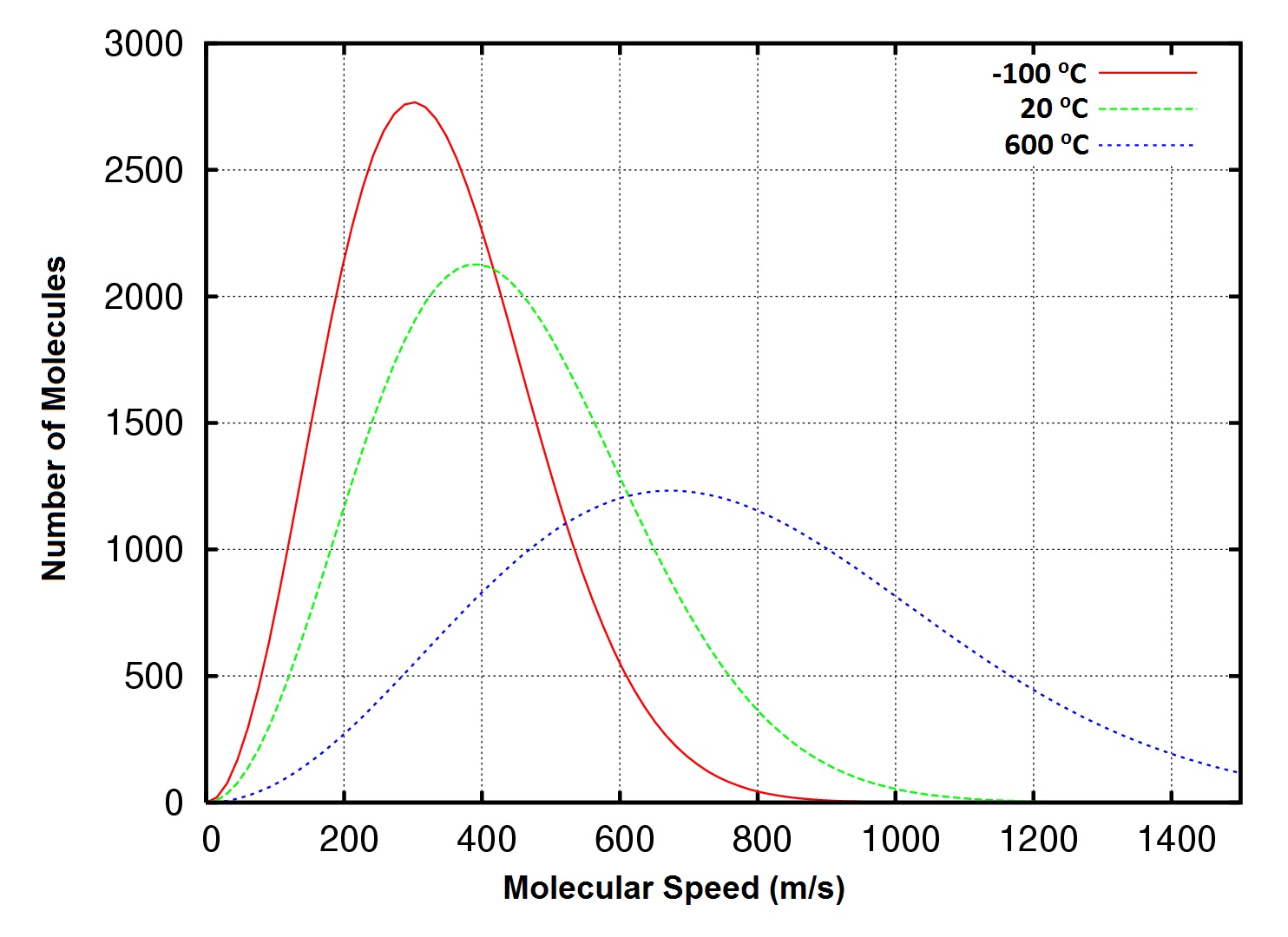
- “Distribution of the Molecular Speeds of Oxygen Gas at −100, 20, and 600°C” by Superborsuk © CC BY-SA (Attribution ShareAlike), adapted by David W. Ball and Jessie A. Key
- Adapted from MaxwellBoltzmann-en.svg by Pdbailey/Public Domain ↵
A model that helps us understand gases and their physical properties at the molecular level.
Energy due to motion.
The speed of molecules having exactly the same kinetic energy as the average kinetic energy of the sample.