Whole Numbers
1 The Place Value System
Have you ever heard the term "whole number"? It might seem like a weird concept: aren’t all numbers whole? I ate six apples this week, or I charged my electric vehicle for three hours yesterday. Those are whole numbers, right?

Well, not all numbers are whole. You could have eaten 3½ apples during a particularly slow apple-eating week, and maybe you didn’t drive your electric vehicle all that much yesterday, so you only had to charge it for 2.3 hours. Those are not whole numbers.
The purpose of this chapter is to define what a whole number is and then learn to work with those whole numbers, be it by adding, subtracting, multiplying, or dividing.
All the chapters in this textbook, including this one, will have examples and exercises geared towards the trades. It contains content relevant to all trades, no matter what trade you are in.
Counting Numbers and Whole Numbers
A number of years ago, a student named Harpreet went through a plumbing apprenticeship program. After completing his schooling and receiving his Red Seal plumbing ticket, he has decided to open up his own plumbing company.
Like most new entrepreneurs, he experienced a steep learning curve, especially when it came to ordering material for jobs and organizing and scheduling when he had a number of jobs on the go.
Although he might not be thinking about counting numbers or whole numbers, he has ended up working with these when ordering materials and during the day-to-day operations of the company.

If we want to start with the very basics, we must start with counting numbers, which are sometimes referred to as natural numbers. These are the most basic units in algebra and the ones we use to count objects. For instance, Harpreet had to order one toilet, two sets of taps, three fittings, four braided hoses, and five chocolate bars (it seems like Harpreet has a bit of a sweet tooth).
One more thing: in counting numbers, there are no decimal or fraction parts. Also, there are no negatives and no zero.
Okay, so we have no zero. But what if we just decided to add a zero to the set of counting numbers? Would that be so bad? No, it wouldn’t, but then we couldn’t call them counting numbers anymore. The set of counting numbers plus zero becomes what is known as the set of whole numbers.
Counting numbers: 1, 2, 3, 4, 5, …
Whole numbers: 0, 1, 2, 3, 4, 5, …
The discovery of the number zero was a big step in the history of mathematics. Don’t ask me why, but apparently it was. As for Harpreet, let’s hope that he bids jobs properly and that his profit doesn’t amount to zero.
The Place Value System
Worried that he might estimate jobs improperly, Harpreet decides he needs some help with estimating and bidding jobs, as well as some help with the books. He calls up his friend Jamieson and asks if he wants to help. Jamieson, who has been in the plumbing industry for a number of years, has had a recurring back injury and figures this might be a good opportunity to rest his back for a while and help his friend out at the same time.
The first job Jamieson bids on is for $931. Take a look at the three numbers in 931 and notice where each one is located. This is very important, because if Jamieson reversed the numbers, he would have bid $139 and most likely lost money on the job.
Writing the correct number relies on what our number system calls the place value system. The 9, the 3, and the 1 are all located in different spots in the larger number, and each of them is called a digit. Putting the digits in the wrong locations could result in disaster when dealing with money and in many other situations.

Here’s a visual example: say I were to take a wallet, open it up, and take out the money. Suppose that wallet had two $100 bills, three $20 bills and one $5 bill. What would the total amount of money be in the wallet?
I would have:
[latex]\LARGE2\times$100=$200[/latex]
[latex]\LARGE3\times$20=$60[/latex]
[latex]\LARGE1\times$5 =$5[/latex]
Adding those up, I would have:
[latex]\LARGE$200+$60+$5=$265[/latex]
Notice that each of the original values has a specific place in the total. Positioning the digits in the reverse order would make it appear as if we had a lot more money than we actually have:
[latex]\LARGE$562[/latex]
This is the importance of the place value system.
Another aspect of this system is known as the base-10 concept. Each position in a number is a specific place. If we use the number 265 as an example, we would see that:
5 = ones place
6 = tens place
2 = hundreds place
Each of the digits in the place value system can have a value anywhere between zero and nine. When the value of a digit increases past nine, we start again at zero but add one to the value of the digit in the next highest place value.
The simplest way to think about this is to go from 9 to 10:
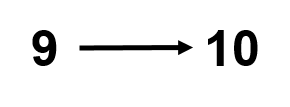
In this case, the ones place goes back to zero and the tens place increases by one.
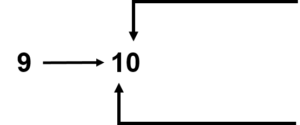
The ones place has gone from nine to zero.
There was no value in the tens place when we started, but now, the tens place has increased by one.
Now, you might be thinking that this really is far too basic to be reading, but these are the building blocks of the language of algebra. Although the example used here is quite simple, when you get to larger and more complex numbers, the mathematical grammar that you are learning here is the basis for understanding more complicated mathematical grammar in the chapters to follow.
Now let's look at a bigger number. One way to understand the place value system is to take a number such as:
[latex]\LARGE5,217,364,958[/latex]
If we were to sound out this number, we would say:
Five billion, two hundred and seventeen million, three hundred and sixty-four thousand, nine hundred and fifty-eight.
It's read that way because each digit corresponds to a certain value in the place value system. Take a look at the following place value chart, in which we start with the ones and work our way up:
| Ones | 8 |
| Tens | 5 |
| Hundreds | 9 |
| Thousands | 4 |
| Ten thousands | 6 |
| Hundred thousands | 3 |
| Millions | 7 |
| Ten millions | 1 |
| Hundred millions | 2 |
| Billions | 5 |
| Ten billions | – |
| Hundred billions | – |
This pattern would continue on into the trillions, quadrillions, quintillions, and so on.
Another common way to express numbers in the place value system is demonstrated in the table below.
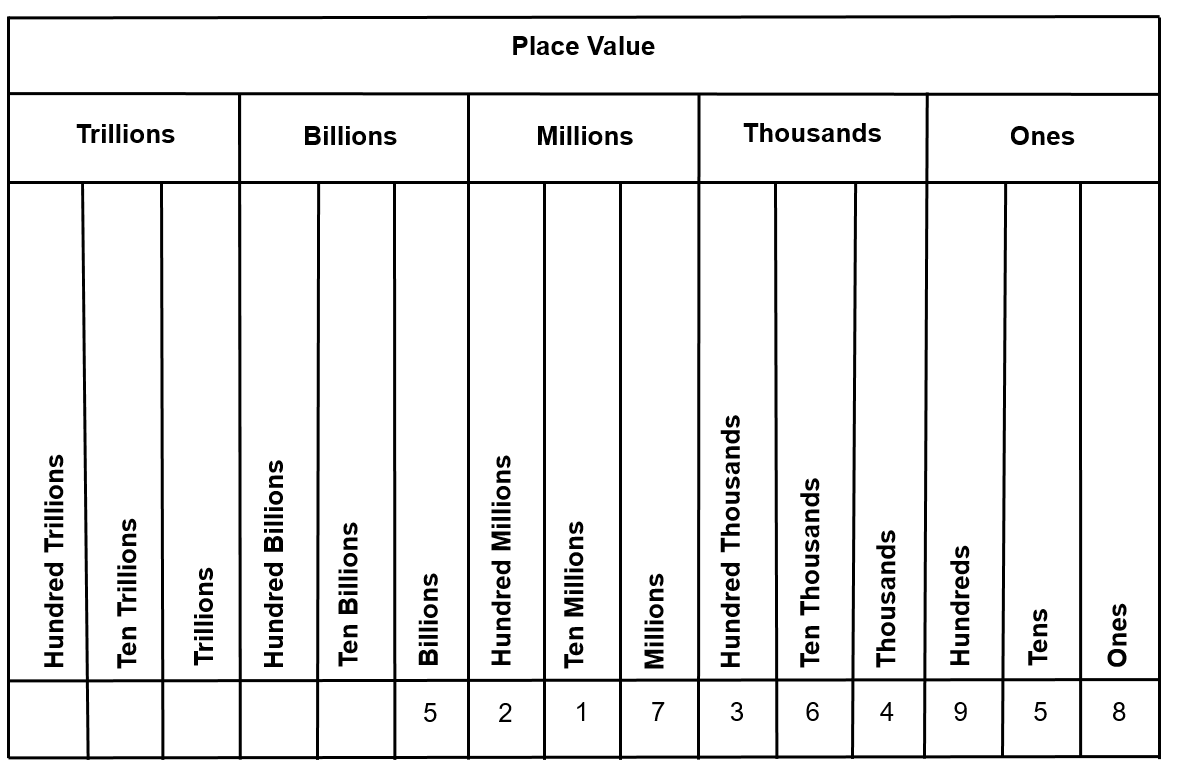
Going from left to right, we get:
- The digit 5 is in the billions place. Its value is 5,000,000,000.
- The digit 2 is in the hundred millions place. Its value is 200,000,000.
- The digit 1 is in the ten millions place. Its value is 10,000,000.
- The digit 7 is in the millions place. Its value is 7,000,000.
- The digit 3 is in the hundred thousands place. Its value is 300,000.
- The digit 6 is in the ten thousands place. Its value is 60,000.
- The digit 4 is in the thousands place. Its value is 4,000.
- The digit 9 is in the hundreds place. Its value is 900.
- The digit 5 is in the tens place. Its value is 50.
- The digit 8 is in the ones place. Its value is 8.
Try an example.
Example
As you go through this question, think of the actual value of each of the digits. For example, the 4 in the leftmost place of the number below represents 40,000,000. Doing this will help you to visualize the value each number actually stands for.
Find the place value of each of the following digits:
[latex]\LARGE45,837,249[/latex]
Use the following layout as a guideline to help you answer the question.
4 = ___________________
5 = ____________________
8 =____________________
3 =____________________
7 =____________________
2 = ____________________
4 = ____________________
9 = ____________________
Inserting the numbers into the table below is also a good place to start:
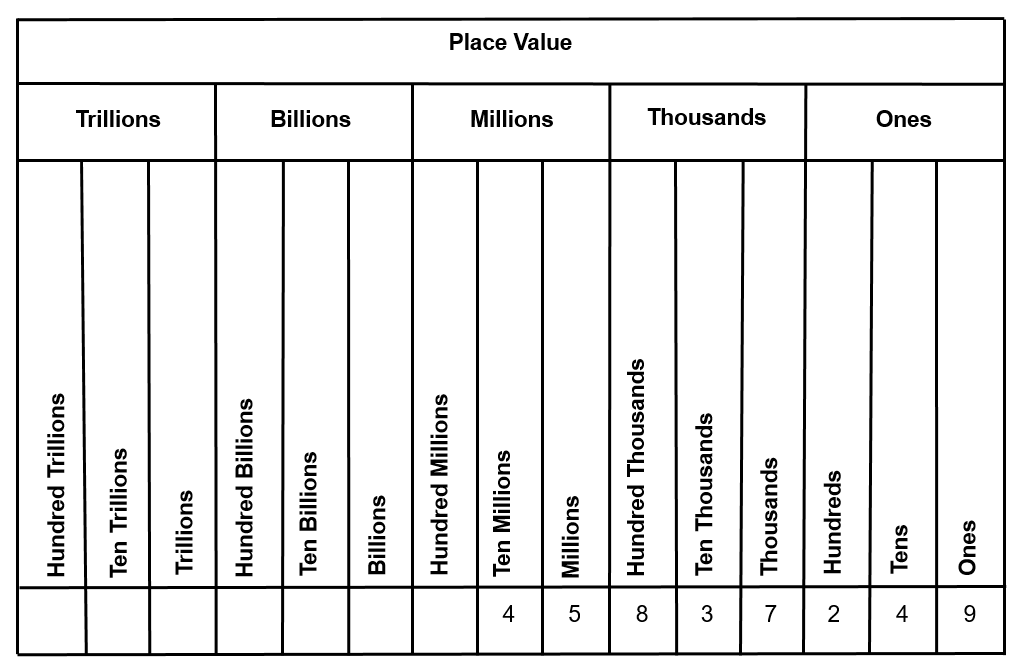
Solution:
Using the table above, you get:
4 = ten millions
5 = millions
8 = hundred thousands
3 = ten thousands
7 = thousands
2 = hundreds
4 = tens
9 = ones
Practice Questions
Try a couple more examples and check out the video answers.
Find the place value of each digit of the following numbers.
Question 1
[latex]\LARGE385,922,102[/latex]
Question 2
[latex]\LARGE20,433,876,011[/latex]

