Unit 4: Multiplication
Topic A: Introduction and Multiplication Facts
Multiplication is a fast way to add. Multiplication is used when the amounts to be added are the same.

How many groups are there? 7
7 groups of 3 = 21
This can be written as a multiplication equation.
7 × 3 = 21
X is the sign that means to multiply. We often say times for this multiplication sign.

4 groups of 2 = 8
4 × 2 = 8 says: 4 times 2 equals 8 or 4 multiplied by 2 equals 8
The result of a multiplication is called the product.
The numbers that are multiplied together are called factors.
7 × 3 = 21 The factors are 7 and 3.
The product is 21.
Exercise One
For each drawing, write the addition equation and find the total. Then write the multiplication equation that describes the same drawing and find the product. Check your work using the answer key at the end of the exercise.
| # | Drawing | Addition equation | Multiplication equation |
|---|---|---|---|
| a. |  |
4 + 4 + 4 = 12 | 3 × 4 = 12 |
| b. | |||
| c. |  |
||
| d. |  |
||
| e. |  |
||
| f. |  |
||
| g. |  |
Answers to Exercise One
- 4 + 4 + 4 = 12, 3 × 4 = 12
- 6 + 6 = 12, 2 × 6 = 12
- 3 + 3 + 3 + 3 + 3 = 15, 5 × 3 = 15
- 5 + 5 + 5 + 5 = 20, 4 × 5 = 20
- 8 + 8 + 8 + 8 = 32, 4 × 8 = 32
Exercise Two
For each drawing, write the addition equation and find the total. Then write the multiplication equation that describes the same drawing and find the product. Check your work using the answer key at the end of the exercise.
| # | Drawing | Addition Equation | Multiplication Equation |
|---|---|---|---|
| a. | 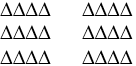 |
||
| b. | 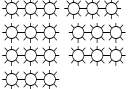 |
||
| c. |  |
||
| d. |  |
||
| e. | 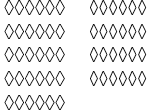 |
Answers to Exercise Two
- 4 + 4 + 4 + 4 + 4 + 4 = 24, 4 × 6 = 24
- 3 + 3 + 3 + 3 + 3 + 3 + 3 = 21, 3 × 7 = 21
- 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5= 40, 5 × 8 = 40
- 7 + 7 + 7 + 7 + 7 = 35, 7 × 5 = 35
- 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 54, 6 × 9 = 54
Exercise Three
Look at the examples. Complete the chart. Check your work using the answer key at the end of the exercise.
Example A: 2 × 3 is read as ―two times three‖ and means 3 + 3
3 × 2 is read as ―three times three‖ and means 2 + 2 + 2
| Equation | “is read as” | means |
|---|---|---|
| 5 × 7 | five times seven | 7 + 7 + 7 + 7 + 7 |
| 2 × 5 | ||
| 3 × 4 | ||
| 5 × 2 | ||
| 4 × 8 | ||
| 2 × 7 | ||
| 3 × 5 | ||
| 2 × 8 | ||
| 3 × 9 | ||
| 6 × 4 | ||
| 7 × 3 |
Answers to Exercise Three
| Equation | “is read as” | means |
|---|---|---|
| 5 × 7 | five times seven | 7 + 7 + 7 + 7 + 7 |
| 2 × 5 | two times five | 5 + 5 |
| 3 × 4 | three times four | 4 + 4 + 4 |
| 5 × 2 | five times two | 2 + 2 + 2 + 2 + 2 |
| 4 × 8 | four times eight | 8 + 8 + 8 + 8 |
| 2 × 7 | two times seven | 7 + 7 |
| 3 × 5 | three times five | 5 + 5 + 5 |
| 2 × 8 | two times eight | 8 + 8 |
| 3 × 9 | three times nine | 9 + 9 + 9 |
| 6 × 4 | six times four | 4 + 4 + 4 + 4 + 4 + 4 |
| 7 × 3 | seven times three | 3 + 3 + 3 + 3 + 3 + 3 + 3 |
Adding will give the answer to multiplication questions but it is very slow, especially if the numbers are large. The times tables are the multiplication facts. You may need to memorize the times tables. You will use the times tables for multiplying, dividing, and working with fractions.
0 × any number = 0
any number × 0 = 0
| 0 × 0 = 0 | 0 × 0 = 0 |
| 0 × 1 = 0 | 1 × 0 = 0 |
| 0 × 2 = 0 | 2 × 0 = 0 |
| 0 × 3 = 0 | 3 × 0 = 0 |
| 0 × 4 = 0 | 4 × 0 = 0 |
| 0 × 5 = 0 | 5 × 0 = 0 |
| 0 × 6 = 0 | 6 × 0 = 0 |
| 0 × 7 = 0 | 7 × 0 = 0 |
| 0 × 8 = 0 | 8 × 0 = 0 |
| 0 × 9 = 0 | 9 × 0 = 0 |
| 0 × 10 = 0 | 10 × 0 = 0 |
| 1 × 0 = 0 |
| 1 × 1 = 1 |
| 1 × 2 = 2 |
| 1 × 3 = 3 |
| 1 × 4 = 4 |
| 1 × 5 = 5 |
| 1 × 6 = 6 |
| 1 × 7 = 7 |
| 1 × 8 = 8 |
| 1 × 9 = 9 |
| 1 × 10 = 10 |
| 0 + 0 = 0 | 2 × 0 = 0 |
| 1 + 1 = 2 | 2 × 1 = 2 |
| 2 + 2 = 4 | 2 × 2 = 4 |
| 3 + 3 = 6 | 2 × 3 = 6 |
| 4 + 4 = 8 | 2 × 4 = 8 |
| 5 + 5 = 10 | 2 × 5 = 10 |
| 6 + 6 = 12 | 2 × 6 = 12 |
| 7 + 7 = 14 | 2 × 7 = 14 |
| 8 + 8 = 16 | 2 × 8 = 16 |
| 9 + 9 = 18 | 2 × 9 = 19 |
| 10 + 10 = 20 | 2 × 10 = 20 |
Can you see a pattern? If you forget a multiplication fact with 2, you can just add.
Example: 2 × 4 = 4 + 4 = 8
2 × 7 = 7 + 7 = 14
The three times table is special. The digits of each product adds up to 3, 6 or 9. You will know your answer is right if you add the digits of the product (the answer for a multiplication question) and the answer is 3, 6 or 9.
| 3 × 0 = 0 | |
| 3 × 1 = 3 | 3 |
| 3 × 2 = 6 | 6 |
| 3 × 3 = 9 | 9 |
| 3 × 4 = 12 | 12 » 1 + 2 = 3 |
| 3 × 5 = 15 | 15 » 1 + 5 = 6 |
| 3 × 6 = 18 | 18 » 1 + 8 = 9 |
| 3 × 7 = 21 | 21 » 2 + 1 = 3 |
| 3 × 8 = 24 | 24 » 2 + 4 = 6 |
| 3 × 9 = 27 | 27 » 2 + 7 = 9 |
| 3 × 10 = 30 | 30 » 3 + 0 = 3 |
Exercise Four
Check out your multiplication facts by doing this exercise as quickly as possible. Find the product. This exercise includes the zero to three times tables. Check your work using the answer key at the end of the exercise. Then, make a list of any multiplication facts you do not know or which are slow – practice them.
- [latex]\begin{array}[t]{r}2\\\times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\\times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\\times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\\times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\\times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\\times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\\times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\\times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\\times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\\times2\\ \hline \\ \end{array}[/latex]
Answers to Exercise Four
- 4
- 9
- 4
- 0
- 7
- 6
- 0
- 3
- 0
- 8
- 12
- 10
- 15
- 0
- 8
- 9
- 1
- 2
- 0
- 6
- 27
- 10
- 16
- 0
- 18
- 0
- 30
- 2
Need Extra Practice?
Domino Practice – Find a partner and ask your instructor for double twelve dominoes.
Use only the following dominoes: 0-0 to 0 -10
1-1 to 1- 10
2-2 to 2- 10
3-3 to 3-10
Turn over the dominoes.
Flip a domino and multiply the two numbers.
Example:
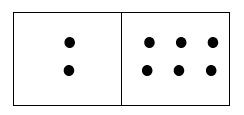
This would be 2 × 6
If you answer correctly, keep the domino.
If you answer incorrectly, flip the domino over.
Study the four times tables below.
| 4 × 0 = 0 |
| 4 × 1 = 4 |
| 4 × 2 = 8 |
| 4 × 3 = 12 |
| 4 × 4 = 16 |
| 4 × 5 = 20 |
| 4 × 6 = 24 |
| 4 × 7 = 28 |
| 4 × 8 = 32 |
| 4 × 9 = 36 |
| 4 × 10 = 40 |
The fives times table is special. If you are multiplying by an even number, the product ends in zero. If you are multiplying by an odd number, the product ends in five.
| 5 × 0 = 0 |
| 5 × 1 = 5 |
| 5 × 2 = 10 |
| 5 × 3 = 15 |
| 5 × 4 = 20 |
| 5 × 5 = 25 |
| 5 × 6 = 30 |
| 5 × 7 = 35 |
| 5 × 8 = 40 |
| 5 × 9 = 45 |
| 5 × 10 = 50 |
The products for the odd numbers 1, 3, 5, 7 and 9 end in five.
The products for the even numbers 2, 4, 6, 8 and 10 end in 10.
Study the six times tables below.
| 6 × 0 = 0 |
| 6 × 1 = 6 |
| 6 × 2 = 12 |
| 6 × 3 = 18 |
| 6 × 4 = 24 |
| 6 × 5 = 30 |
| 6 × 6 = 36 |
| 6 × 7 = 42 |
| 6 × 8 = 48 |
| 6 × 9 = 54 |
| 6 × 10 = 60 |
Exercise Five
Check out your multiplication facts by doing this exercise as quickly as possible. Find the product. This exercise includes the four to six times tables. Check your work using the answer key at the end of the exercise. Then, make a list of any multiplication facts you do not know or which are slow – practice them.
- [latex]\begin{array}[t]{r}5\\ \times 6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times 2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times 1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times 0\\ \hline \\ \end{array}[/latex]
Answers to Exercise Five
- 30
- 6
- 28
- 35
- 60
- 8
- 20
- 18
- 16
- 30
- 24
- 28
- 54
- 20
- 10
- 0
- 35
- 36
- 0
- 50
- 36
- 5
- 30
- 12
- 45
- 12
- 4
- 0
Need Extra Practice?
Card Practice – Find a partner and ask your instructor for a deck of cards.
Take out all the jacks, queens and kings. You will only need the aces to tens.
Choose a times table to practice.
Example: to practice the 5 times table
- Choose a single 5 card and place it face up.
- Shuffle the remainder of the cards.
- From the shuffled cards, place one card face up next to the five.
- Multiply. Have your partner check your answer.
- If the answer is correct, leave it on the pile.
- If the answer is incorrect, place the card in front of you.
- Keep turning cards over until there are no cards left.
- Reshuffle any cards in front of you.
- Place a card on the pile and multiply.
- When all the cards are in the pile, you are done.
- Choose a different times table to practice and start again.
Exercise Six
Check out your multiplication facts by doing this exercise as quickly as possible. Find the product. This exercise includes the zero to six times tables. Check your work using the answer key at the end of the exercise. Then, make a list of any multiplication facts you do not know or which are slow – practice them.
- [latex]\begin{array}[t]{r} 6\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 5\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 0\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 1\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 2\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 2\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 5\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 5\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 2\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 2\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 1\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 5\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 1\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 1\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 2\\ \times9\\ \hline \\ \end{array}[/latex]
Answers to Exercise Six
- 18
- 35
- 0
- 24
- 5
- 6
- 9
- 8
- 4
- 42
- 40
- 36
- 5
- 8
- 30
- 10
- 3
- 15
- 24
- 42
- 30
- 12
- 0
- 40
- 9
- 6
- 0
- 54
- 36
- 0
- 21
- 18
Exercise Seven
- [latex]\begin{array}[t]{r}1\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\ \times9\\ \hline \\ \end{array}[/latex]
Answers to Exercise Seven
- 1
- 60
- 4
- 0
- 35
- 40
- 2
- 7
- 0
- 24
- 2
- 0
- 3
- 40
- 42
- 20
- 30
- 30
- 0
- 10
- 30
- 18
- 28
- 32
- 36
- 25
- 27
- 48
- 12
- 24
- 21
- 18
Study the seven times table below.
| 7 × 0 = 0 |
| 7 × 1 = 7 |
| 7 × 2 = 14 |
| 7 × 3 = 21 |
| 7 × 4 = 28 |
| 7 × 5 = 35 |
| 7 × 6 = 42 |
| 7 × 7 = 49 |
| 7 × 8 = 56 |
| 7 × 9 = 63 |
| 7 × 10 = 70 |
Study the eight times table below.
| 8 × 0 = 0 |
| 8 × 1 = 8 |
| 8 × 2 = 16 |
| 8 × 3 = 24 |
| 8 × 4 = 32 |
| 8 × 5 = 40 |
| 8 × 6 = 48 |
| 8 × 7 = 56 |
| 8 × 8 = 64 |
| 8 × 9 = 72 |
| 8 × 10 = 80 |
The nines times table is special. The digits of every product add up to nine. Also the first digit in the product is one less than the number you are multiplying.
| 9 × 0 = 0 | |
| 9 × 1 = 9 | 9 |
| 9 × 2 = 18 | 18 » 1 + 8 = 9 |
| 9 × 3 = 27 | 27 » 2 + 7 = 9 |
| 9 × 4 = 36 | 36 » 3 + 6 = 9 |
| 9 × 5 = 45 | 45 » 4 + 5 = 9 |
| 9 × 6 = 54 | 54 » 5 + 4 = 9 |
| 9 × 7 = 63 | 63 » 6 + 3 = 9 |
| 9 × 8 = 72 | 72 » 7 + 2 = 9 |
| 9 × 9 = 81 | 81 » 8 + 1 = 9 |
| 9 × 10 = 90 | 90 » 9 + 0 = 9 |
Exercise Eight
Check out your multiplication facts by doing this exercise as quickly as possible. Find the product. This exercise includes the seven to nine times tables.
- [latex]\begin{array}[t]{r}7\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times8\\ \hline \\ \end{array}[/latex]
Answers to Exercise Eight
- 28
- 24
- 0
- 14
- 54
- 0
- 64
- 9
- 48
- 18
- 63
- 0
- 36
- 49
- 8
- 90
- 35
- 32
- 27
- 70
- 64
- 45
- 7
- 16
- 21
- 40
- 81
- 56
Exercise Nine
Check out your multiplication facts by doing this exercise as quickly as possible. Find the product. This exercise includes the seven to nine times tables. Check your work using the answer key at the end of the exercise. Then, make a list of any multiplication facts you do not know or which are slow – practice them.
- [latex]\begin{array}[t]{r}9\\ \times0\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times10\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times0\\ \hline \\ \end{array}[/latex]
Answers to Exercise Nine
- 0
- 56
- 35
- 45
- 42
- 72
- 40
- 56
- 72
- 80
- 28
- 90
- 48
- 49
- 27
- 72
- 36
- 24
- 21
- 72
- 64
- 81
- 14
- 16
- 63
- 8
- 54
- 0
Need Extra Practice?
Domino Practice – Find a partner and ask your instructor for double twelves dominoes.
Use only the following dominoes: 1-0 to 0 -10
1-2 to 1- 10
2-2 to 2- 10
3-3 to 3-10
4-4 to 4-10
5-5 to 5-10
6-6 to 6-10
7-7 to 7-10
8-8 to 8-10
9-9 to 9-10
10-10
Turn over the dominoes
Flip a domino and multiply the two numbers
Example:
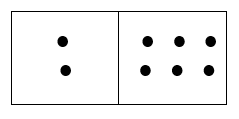
This would be 2 × 6
If you answer correctly, keep the domino.
Exercise Ten
Check out your multiplication facts by doing this exercise as quickly as possible.
- [latex]\begin{array}[t]{r}5\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}3\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}9\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}6\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times2\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 9\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}7\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}8\\ \times1\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}2\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}4\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}5\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}1\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r}0\\ \times9\\ \hline \\ \end{array}[/latex]
Answers to Exercise Ten
- 20
- 21
- 30
- 63
- 18
- 42
- 2
- 12
- 45
- 3
- 42
- 18
- 4
- 12
- 81
- 15
- 36
- 40
- 28
- 6
- 7
- 10
- 64
- 72
- 32
- 49
- 8
- 12
- 32
- 30
- 7
- 0
Make a list of any errors that you have made and of the facts that you had to really think about.
As you know, it is very important to memorize the times tables. Use the times table chart on the next page until you have all the multiplication facts memorized. It is better to look up the right answer than use the wrong product. Finding the right product and saying the facts to yourself will help you learn.
Times Table Chart
Let’s say you do not know the product of 8 × 9.
- Find the first factor (8) in the column at the left. Find the second factor (9) in the top row.
- Go across the row from the 8 and straight down the column from the 9.
- The lines meet at the product which is 72 … Try it! Now try finding the products of some other multiplication facts.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Times Tables are very difficult to memorize. Here’s a technique that may help you to learn them.
An instructor used this technique to teach his students the times tables. It does require you to do some work and will take some time. But, if you are willing, you will learn them. Here’s how it works.
Most people can only memorize three things; as soon as they try to memorize a fourth thing, they lose one of the first three. So, instead of trying to memorize the complete times table (which is 121 things), just do three.
- 9 × 9 = 81
- 8 × 8 = 64
- 8 × 9 = 72
If you know any of these already, for example, you automatically know that 9 × 9 = 81, choose another one, like 7 × 7 = 49.
Write these three on small cards or pieces of paper in three different ways:
9 × 9 = 81 9 × 9 = 9 × = 81
8 × 8 = 64 8 x 8 = 8 × = 64
8 × 9 = 72 8 x 9 = 8 × = 72
Note: 8 × 9 = 72 and 9 × 8 = 72. Both are the same, so when you learn 8 × 9 you will also know 9 × 8. You will have learned part of the 8 times table and part of the 9 times table.
Do a number of these and stick them up around your house – over the kitchen sink, on your bathroom mirror, on your closet door, etc. Then, every time you see one of these, run through it in your mind. It only takes about 5 seconds each time. After about a week or two, you will have learned these three. If anyone were to ask you what 9 9 was, you would automatically know that it is 81. You wouldn’t have to figure it out; you would know it.
And, once you know it, you will never forget it.
Once you have master these three, do three more, like 7 × 7 = 49, 7 × 8 = 56, 7 × 9 = 63. Again, make up small cards and put them all over your house. In another week or so, you will have learned these and can do another three.
If you are willing to do the work, you will learn your times tables. And, once you learn them, you will never forget them. That will make your work in mathematics much easier, and maybe even more fun. Try it! It does work.
Multiplying Across
So far you have only been multiplying numbers when they are up and down or vertical.
Example: 4 × 5 = 20
Another way to multiply numbers is across or horizontally.
Example: 4 × 5 = 20
In math, sometimes you will need to work from left to right.
Exercise Eleven
Practice multiplying across or horizontally. Find the product. This exercise includes the zero to nine times tables.
- 2 × 6 =
- 5 × 4 =
- 7 × 3 =
- 3 × 6 =
- 8 × 5 =
- 4 × 7 =
- 9 × 2 =
- 6 × 5 =
- 5 × 3 =
- 3 × 8 =
- 7 × 7 =
- 2 × 9 =
- 4 × 6 =
- 6 × 9 =
- 8 × 8 =
- 9 × 4 =
- 3 × 9 =
- 4 × 4 =
- 6 × 7 =
- 9 × 6 =
Answers to Exercise Eleven
- 12
- 20
- 21
- 18
- 40
- 28
- 18
- 30
- 15
- 24
- 49
- 18
- 24
- 54
- 64
- 36
- 27
- 16
- 42
- 54
Topic A: Self-Test
Mark /20 Aim 17/20
- Find the products. Be sure to check your answers. (16 marks)
- [latex]\begin{array}[t]{r} 3\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times4\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 7\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 8\\ \times3\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 9\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 7\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times8\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 8\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 2\\ \times5\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 3\\ \times7\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 4\\ \times6\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 5\\ \times9\\ \hline \\ \end{array}[/latex]
- [latex]\begin{array}[t]{r} 6\\ \times7\\ \hline \\ \end{array}[/latex]
- Find the products. Be sure to check your answers. (4 marks)
- 7 × 5 =
- 8 × 6 =
- 9 × 8 =
- 7 × 4 =
Answers to Topic A Self-Test
-
- 9
- 36
- 24
- 56
- 24
- 45
- 27
- 54
- 49
- 32
- 72
- 10
- 21
- 24
- 45
- 42
-
- 35
- 48
- 72
- 28

