Unit 5: Making Change, Time & Perimeter

Topic E: Perimeter

Perimeter is from the Greek language. Peri means “around”. Perimeter is the distance around something. If you walked around the outside of your building, you would have walked close to the perimeter of the building. (The actual perimeter would be the outside wall which is a little tricky to walk on!) A fence around a field is at the perimeter of the field. In this sense, we are using perimeter to mean “the outside edge”. The length of the entire fence is the measure of the perimeter.

Example A

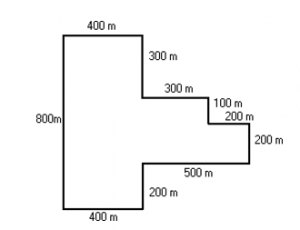
Picture yourself going for a walk, starting at the door of your building.

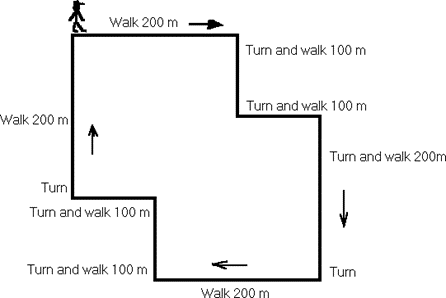
walk 200m, turn and walk 100 m, turn and walk 100 m, turn and walk 200 m, turn and walk 200 m, turn and walk 100 m, turn and walk 100 m, turn and walk 200 m,

Your walk was in the shape of an octagon. How far did you walk? When you add together all the distances, you get 1 200 m.

You have just found the perimeter of an octagon.

Example B

The new memorial park was built in an interesting shape. The park is a hexagon. A walking path goes around the perimeter of the park.

How long is the path?

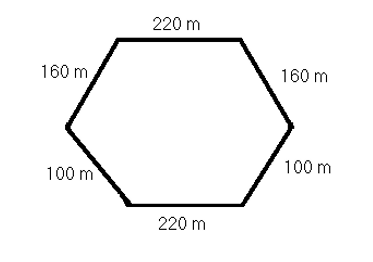
length of the sides of the hexagon: 220m, 160m, 100m, 220m 100m, 160m.

Add the measure of each side of the park. The perimeter of this hexagon is 960 m.

To find the perimeter of a polygon, add the lengths of all the sides together.

Exercise One

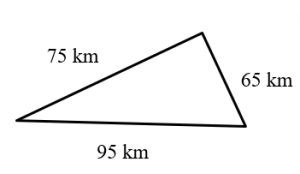
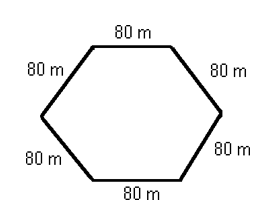
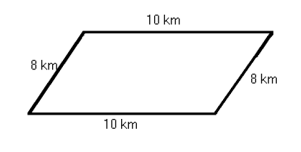
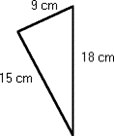
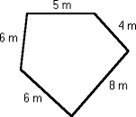
Find the perimeter of each figure. Be sure to include the units of measure in your answer. Check your work using the answer key at the end of the exercise.

  1. a triangle whose sides are 75km, 65km, 95km
  2. a hexagon whose sides are all 80m
  3. a parallelogram whose sides are 8km, 10 km, 8 km, 10 km
  4. a rectangle whose length is 12 km, width is 3 km
  5. a decagon whose sides are 400m, 300m, 300m, 100m, 200m, 200m, 500m, 200m, 400m, 800m

Answers to Exercise One

  1. 235 metres
  2. 480 metres
  3. 36 kilometres
  4. 30 kilometres
  5. 3400 kilometres

Finding the Perimeter of a Square

Write the definition of a square.

By definition then, a square has four sides that are all congruent (have the same measure). To find the perimeter you can add the four sides.

a square whose sides are 8 cm

Perimeter = 8 cm + 8 cm + 8 cm + 8 cm = 32 cm

Exercise Two

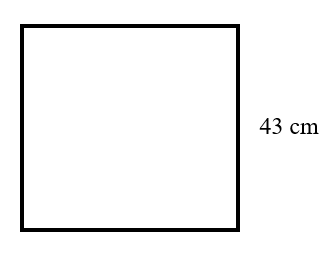
Find the perimeter of the squares described in each question. The measure of one side has been given. Be sure to include the units of measure in your answer. Check your work using the answer key at the end of the exercise.

  1. s = 75 m
    p = 75 m + 75 m + 75 m + 75 m
    p =
  2. s = 12 m
    p =
  3. s = 100 km
    p =
  4. s = 50 cm
    p =
  5. s = 130 m
    p =
  6. s = 1 000 km
    p =
  7. s = 165 m
    p =
  8. s = 325 m
    p =
  9. s = 68 cm
    p =
  10. s = 85 mm
    p =

Answers to Exercise Two

  1. 300 metres
  2. 48 millimetres
  3. 400 kilometres
  4. 200 centimetres
  5. 520 metres
  6. 4000 kilometres
  7. 660 metres
  8. 1300 metres
  9. 272 centimetres
  10. 340 millimetres

Problems using the Perimeters of Squares

Example C

Ted needs to build a fence around his swimming pool. The swimming pool with its deck is a square shape that measures 35 m per side. How much fencing must Ted buy?

Step 1: Question.

How much fencing must Ted buy?

Step 2: Find the needed information—drawing a sketch is often helpful.

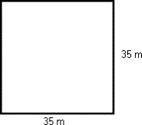
a square whose sides are 35m

– fence around a square pool s = 35m

Step 3: Operations.

The fence is a perimeter, so find the perimeter of a square.

P = 35 m + 35 m + 35 m + 35 m

P = 140 m of fence Ted must buy 140 m of fencing.

Exercise Three

Solve these problems using perimeters of squares. The problems may need two operations. Be sure to include the units of measure in your answer. Check your work using the answer key at the end of the exercise.

  1. The campground security officer walks around the outside of the campground four times every evening. The campground is 800 m square. How far does the officer walk in these patrols each night? Note: 800 m square is a common way of saying “a square with sides that measure 800 m.”
  2. Lee is going to install base boards in the recreation room he has built in his basement. The room is five metres square. The baseboard material is expensive, so he will be sure to deduct 1 m for each of the two doorways. How much baseboard material does he need to buy?
  3. Phil is going to fence his large 50 m square vegetable garden to keep the deer out. The fence will be made with four strands of barbed wire. How much barbed wire should Phil buy? The fence will look like this:

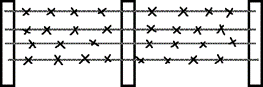
Answers to Exercise Three

  1. 12800 metres
  2. 18 metres
  3. 800 metres

Finding the Perimeter of a Rectangle

Write the definition of a rectangle.

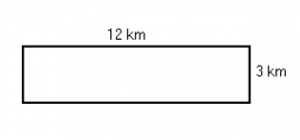
Example D

length (l) = 12 m

width (w) = 3 m

To find the perimeter you can find the sum of 12 m + 3 m + 12 m + 3 m = 30 m

Example E

Find the perimeter of a rectangle 25 m long and 15 m wide.

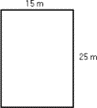
P = 15 m + 25 m + 15 m + 25 m = 80 m

Exercise Four

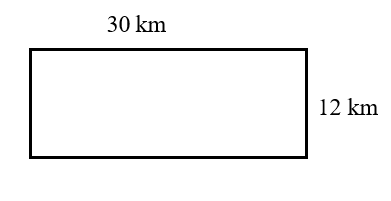
Find the perimeter of the rectangles described below. Draw and label a sketch for each. Be sure to include the units of measure in your answer. Check your work using the answer key at the end of the exercise.

  1. L = 10 cm
    w = 6 cm
    p =
  2. L = 100 km
    w = 70 km
    p =
  3. L = 15 mm
    w = 10 mm
    p =
  4. L = 97 cm
    w = 35 cm
    p =
  5. L = 400 km
    w = 100 km
    p =
  6. L = 42 m
    w = 67 m
    p =
  7. L = 132 m
    w = 76 m
    p =
  8. L = 196 cm
    w = 28 cm
    p =

Answers to Exercise Four

  1. 32 centimetres
  2. 340 kilometres
  3. 50 millimetres
  4. 64 centimetres
  5. 1000 kilometres
  6. 218 metres
  7. 416 metres
  8. 448 centimetres

Problems using Perimeters of Rectangles

Exercise Five

Solve these problems. Draw and label a sketch for each. Be sure to include the units of measure in your answer. Check your work using the answer key at the end of the exercise.

  1. Janice plans to sew lace on the edge of a tablecloth that is 132 cm in width and 218 cm long. How much lace does she need?
  2. One physical education teacher starts each class by having everyone jog around the school 4 times. The school is rectangular (shaped like a rectangle) and 160 m long and 95 m wide. About how far do the students jog each class? Note: 160 m long and 95 m wide may be written as “160 m by 95 m”.
  3. How many metres of baseboard are needed for a rectangular room 4 m by 3 m? Deduct 1 m for each of the two doorways.
  4. Dennis likes to cycle 30 km daily around a cycle path at a local park. The park is rectangular and measures 3 km in width and 5 km in length. How far does Dennis cycle if he rides around the park twice?
  5. Calculate the total amount of weather-stripping needed to go around these windows in a house.
    • 3 windows each measuring 76 cm by 122 cm
    • 2 windows each measuring 152 cm by 135 cm
  6. The Nuoris are going to replace the fascia board (the trim at the edge of a roof) with new pressure-treated cedar board. Their flat roof is 14 m by 12 m. How much fascia board is needed?

Answers to Exercise Five

  1. 700 centimetres
  2. 2 040 metres
  3. 12 metres
  4. 32 kilometres
  5. 2336 centimetres
  6. 52 metres

Topic E: Self-Test

Mark    /6    Aim 5/6

  1. Find the perimeter of each shape. (4 marks)
    1. a triangle whose sides are 9cm, 15cm, 18cm
    2. a square whose sides are 43cm
    3. a rectangle that is 3km long and 12 km wide
    4. a pentagon whose sides are 5m, 4m, 8m, 6m, 6m
  2. Word Problems. Draw and label a sketch for each. Be sure to include the units of measure in your answer. (2 mark)
    1. How much chrome edging will Juanita need for a kitchen table 121 cm square?
    2. Than is going to frame a fabulous poster that is 100 cm by 70 cm. How much framing material should he buy?

Answers to Topic E Self-Test

    1. 42 centimetres
    2. 172 centimetres
    3. 84 kilometres
    4. 29 metres
    1. 484 centimetres
    2. 340 centimetres

License

Icon for the Creative Commons Attribution 4.0 International License

Adult Literacy Fundamental Mathematics: Book 2 – 2nd Edition Copyright © 2022 by Wendy Tagami and Liz Girard is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book