Unit 4: Adding & Subtracting Common Fractions
Topic A: Adding Common Fractions
Vocabulary Review:
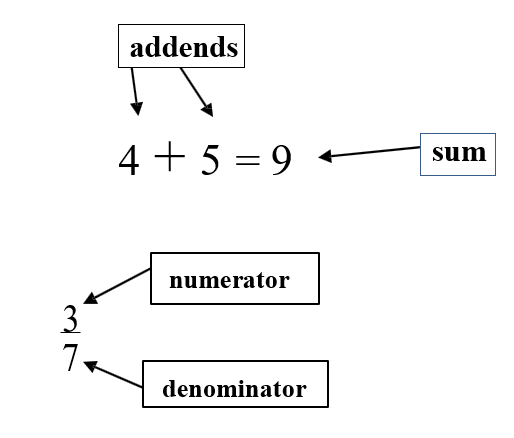
Like Fractions: Fractions that have the same denominator
Example: [latex]\tfrac{1}{4}[/latex], [latex]\tfrac{2}{4}[/latex], [latex]\tfrac{3}{4}[/latex], [latex]\tfrac{4}{4}[/latex], etc.
Adding and subtracting fractions has some different rules from multiplying and dividing.
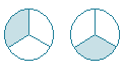
There are two cakes that are left over. There is 1 piece of each cake left. If you were to put all the pieces left onto one plate, how much cake would you have?
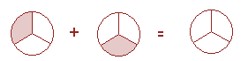
Shade in your answer here
If you made your plate like this: 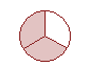 then you are right!
then you are right!
Try this example:

The answer is:

What you are doing is adding two like fractions.
- You are moving pieces of fractions that are the same size into one whole shape. The pieces do not change size, so the denominator must stay the same size.
- When adding two fractions, your answer is a fraction.
Look back at the two examples.
When you add fractions, does the denominator or the numerator stay the same?
Look at the next two examples:

[latex]\dfrac{1}{4} + \dfrac{2}{4} = \dfrac{3}{4}[/latex]

[latex]\dfrac{1}{5}+ \dfrac{2}{5}+ \dfrac{1}{5} = \dfrac{4}{5}[/latex]
Exercise 1
Try a few for yourself
-
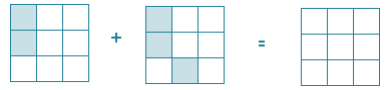
[latex]\dfrac{2}{9} + \dfrac{3}{9} = \dfrac{ }{9}[/latex]

[latex]\dfrac{2}{4} + \dfrac{1}{4} = \dfrac{ }{4}[/latex]
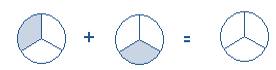
[latex]\dfrac{1}{3} + \dfrac{1}{3} = \dfrac{ }{3}[/latex]

[latex]\dfrac{3}{6} + \dfrac{3}{6} = \dfrac{ }{6}[/latex]
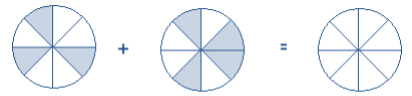
[latex]\dfrac{3}{8} + \dfrac{4}{8} = \dfrac{ }{8}[/latex]
Answers to Exercise 1
- [latex]\tfrac{5}{9}[/latex]
- [latex]\tfrac{3}{4}[/latex]
- [latex]\tfrac{2}{3}[/latex]
- [latex]\tfrac{5}{6}[/latex]
- [latex]\tfrac{7}{8}[/latex]
Exercise 2
Now find the answers to the additions without diagrams.
- [latex]\dfrac{2}{4} + \dfrac{1}{4} = \dfrac{ }{4}[/latex]
- [latex]\dfrac{1}{3} + \dfrac{1}{3} = \dfrac{ }{3}[/latex]
- [latex]\dfrac{1}{5} + \dfrac{1}{5} = \dfrac{ }{5}[/latex]
- [latex]\dfrac{2}{11} + \dfrac{7}{11} = \dfrac{ }{11}[/latex]
Answers to Exercise 2
- [latex]\tfrac{3}{4}[/latex]
- [latex]\tfrac{2}{3}[/latex]
- [latex]\tfrac{2}{5}[/latex]
- [latex]\tfrac{9}{11}[/latex]
Exercise 3
Add these common fractions.
- [latex]\dfrac{1}{5} + \dfrac{2}{5} =[/latex]
- [latex]\dfrac{3}{6} + \dfrac{2}{6} =[/latex]
- [latex]\dfrac{3}{7} + \dfrac{2}{7} =[/latex]
- [latex]\dfrac{3}{10} + \dfrac{6}{10} =[/latex]
- [latex]\dfrac{14}{20} + \dfrac{3}{20} =[/latex]
- [latex]\dfrac{7}{37} + \dfrac{19}{37} =[/latex]
Answers to Exercise 3
- [latex]\tfrac{3}{5}[/latex]
- [latex]\tfrac{5}{6}[/latex]
- [latex]\tfrac{5}{7}[/latex]
- [latex]\tfrac{9}{10}[/latex]
- [latex]\tfrac{17}{20}[/latex]
- [latex]\tfrac{26}{37}[/latex]
Sometimes the sum of a fraction will need to be reduced (take a look at this example to remind yourself how to do this).
Example A
[latex]\dfrac{2}{8} + \dfrac{2}{8} = \dfrac{4}{8}\rightarrow\dfrac{4÷ 4}{8÷ 4} = \dfrac{1}{2}[/latex]
Example B
[latex]\dfrac{3}{4} + \dfrac{3}{4} = \dfrac{6}{4}\rightarrow\dfrac{6÷ 2}{4÷ 2}=\dfrac{3}{2}= 1\dfrac{1}{2}[/latex]
Exercise 4
Find the sums to the following additions. Make sure your answer is in the lowest terms.
- [latex]\dfrac{1}{4} + \dfrac{1}{4} =[/latex]
- [latex]\dfrac{1}{3} + \dfrac{1}{3} =[/latex]
- [latex]\dfrac{3}{10} + \dfrac{2}{10} =[/latex]
- [latex]\dfrac{7}{25} + \dfrac{8}{25} =[/latex]
- [latex]\dfrac{3}{5} + \dfrac{1}{5} =[/latex]
- [latex]\dfrac{9}{27} + \dfrac{12}{27} =[/latex]
Answers to Exercise 4
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{3}{5}[/latex]
- [latex]\dfrac{4}{5}[/latex]
- [latex]\dfrac{7}{9}[/latex]
So far all your answers have been less than one (a proper fraction). Sometimes adding fractions can result in more than one whole.
Look at this example:

[latex]\dfrac{2}{4} + \dfrac{3}{4}=\dfrac{4}{4}\text{ and }\dfrac{1}{4} \left(\text{or}\dfrac{5}{4}\right)[/latex]
There are not enough parts in the first square to hold all your shaded parts, so you need to draw a second square to hold the extra shaded parts.
You would also have to convert this answer from an improper fraction to a mixed number:
[latex]\dfrac{5}{4} = 1\dfrac{1}{4}[/latex]
Exercise 5
Try these additions. Remember to always reduce!

[latex]\tfrac{4}{6}+\tfrac{5}{6} =[/latex]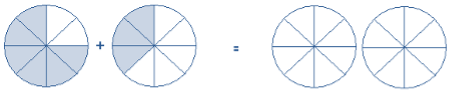
[latex]\tfrac{6}{8}+\tfrac{3}{8} =[/latex]
[latex]\tfrac{3}{4}+\tfrac{3}{4}=[/latex]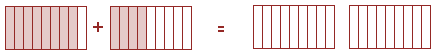
[latex]\tfrac{8}{9}+\tfrac{4}{9} =[/latex]
[latex]\tfrac{3}{5}+\tfrac{4}{5} =[/latex]
Answers to Exercise 5
- [latex]1\tfrac{1}{2}[/latex]
- [latex]1\tfrac{1}{8}[/latex]
- [latex]1\tfrac{1}{2}[/latex]
- [latex]1\tfrac{1}{3}[/latex]
- [latex]1\tfrac{2}{5}[/latex]
Example C
Sometimes you will have to add 3 or more fractions together.

[latex]\dfrac{2}{3} + \dfrac{1}{3} + \dfrac{2}{3} = \dfrac{5}{3} = 1\dfrac{2}{3}[/latex]
Example D

[latex]\dfrac{1}{4} + \dfrac{2}{4} + \dfrac{1}{4} + \dfrac{3}{4} = \dfrac{7}{4}[/latex]
Exercise 6
Add these common fractions. Be sure your answers are in lowest terms.
- [latex]\dfrac{2}{3} + \dfrac{1}{3} = \dfrac{3}{3} = 1[/latex]
- [latex]\dfrac{7}{10} + \dfrac{3}{10} =[/latex]
- [latex]\dfrac{3}{5} + \dfrac{2}{5} =[/latex]
- [latex]\begin{array}{rr}&\dfrac{3}{4}\\+&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{5}{6}\\+&\dfrac{5}{6}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{4}{8}\\+&\dfrac{3}{8}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{1}{8}\\+&\dfrac{3}{8}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{2}{5}\\&\dfrac{3}{5}\\+&\dfrac{3}{5}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{3}{6}\\&\dfrac{1}{6}\\ +&\dfrac{1}{6}\\ \hline&\end{array}[/latex]
Answers to Exercise 6
- 1
- 1
- 1
- [latex]1\tfrac{2}{3}[/latex]
- [latex]\tfrac{7}{8}[/latex]
- [latex]\tfrac{1}{2}[/latex]
- [latex]1\tfrac{3}{5}[/latex]
- [latex]\tfrac{5}{6}[/latex]
Adding Mixed Numbers
To add mixed numbers
- Be sure the denominators are the same.
- Add the common fractions.
- Add the whole numbers.Simplify the common fraction.
Example E
[latex]\begin{array}{rr}&3\dfrac{1}{8}\\+&2\dfrac{3}{8}\\ \hline\end{array}[/latex]
[latex]5\dfrac{4}{8}[/latex] = [latex]5\dfrac{1}{2}[/latex]
[latex]\dfrac{4}{8}[/latex] = [latex]\dfrac{4}{8}\left(\dfrac{÷4}{÷4}\right )[/latex] = [latex]\dfrac{1}{2}[/latex]
Example F
[latex]\begin{array}{rr}&12\dfrac{1}{3}\\+&6\dfrac{1}{3}\\\hline&18\dfrac{2}{3}\end{array}[/latex]
Exercise 7
Add the following numbers. Reduce the answers to lowest terms.
- [latex]\begin{array}{rr}&6\dfrac{1}{12}\\+&8 \dfrac{5}{12}\\ \hline \end{array}[/latex]
[latex]14 \dfrac{6}{12} = 14 \dfrac{1}{2}[/latex] - [latex]\begin{array}{rr}&22\dfrac{1}{6}\\+&14\dfrac{6}{12}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&8\dfrac{1}{4}\\+&3\dfrac{1}{4}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&18\dfrac{1}{2}\\+&10\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&4\dfrac{1}{10}\\+&\dfrac{3}{10}\\ \hline\end{array}[/latex]
Answers to Exercise 7
- [latex]36\tfrac{1}{3}[/latex]
- [latex]11\tfrac{1}{2}[/latex]
- [latex]28\tfrac{1}{2}[/latex]
- [latex]4\tfrac{2}{5}[/latex]
Exercise 8
Add these numbers. Give your answers in lowest terms.
- [latex]\begin{array}{ll}&6\dfrac{4}{5}\\+&3\dfrac{2}{5}\\ \hline\end{array}[/latex]
[latex]9\dfrac{6}{5}=10\dfrac{1}{5}[/latex] - [latex]\begin{array}{ll}&9\dfrac{1}{3}\\+&2\dfrac{2}{3}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{ll}&3\dfrac{3}{8}\\+&12\dfrac{7}{8}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{ll}&100\dfrac{7}{10}\\+&50\dfrac{5}{10}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{ll}&3\dfrac{4}{7}\\+&6\dfrac{5}{7}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{ll}&8\dfrac{4}{5}\\+&\dfrac{4}{5}\\ \hline\end{array}[/latex]
Answers to Exercise 8
- 12
- [latex]16\tfrac{1}{4}[/latex]
- [latex]151\tfrac{1}{5}[/latex]
- [latex]10\tfrac{2}{7}[/latex]
- [latex]9\tfrac{3}{5}[/latex]
If you are not comfortable with this work so far, talk to your instructor and get some more practice before you go ahead.
The next question is:
What happens when two fractions in an addition (the addends) do not have the same denominator? If the addends do not have a common denominator, you will need to find equivalent fractions to make the addends have a common denominator.
Read on to find out how!
Multiples and Least Common Multiples (LCM)
When you learned the multiplication tables you learned the multiples of each number. Multiples are the answers when you multiply a whole number by 1, 2, 3, 4, 5, 6, 7, and so on.
| The multiples of 2 | The multiples of 6 |
|---|---|
| [latex]2\times1 = \bf{2}[/latex] | [latex]6\times1 = \bf{6}[/latex] |
| [latex]2\times2 = \bf{4}[/latex] | [latex]6\times2 = \bf{12}[/latex] |
| [latex]2\times3 = \bf{6}[/latex] | [latex]6\times3 = \bf{18}[/latex] |
| [latex]2\times4 = \bf{8}[/latex] | [latex]6\times4 = \bf{24}[/latex] |
| [latex]2\times5 = \bf{10}[/latex] | [latex]6\times5 = \bf{30}[/latex] |
| [latex]2\times6 = \bf{12}[/latex] | [latex]6\times6 = \bf{36}[/latex] |
| [latex]2\times7 = \bf{14}[/latex] | [latex]6\times7 = \bf{42}[/latex] |
| [latex]2\times8 = \bf{16}[/latex] | [latex]6\times8 = \bf{48}[/latex] |
| [latex]2\times9 = \bf{18}[/latex] | [latex]6\times9 = \bf{54}[/latex] |
| [latex]2\times10 = \bf{20}[/latex] | [latex]6\times10 = \bf{60}[/latex] |
| [latex]2\times11 = \bf{22}[/latex] | [latex]6\times11 = \bf{66}[/latex] |
| [latex]2\times12 = \bf{24}[/latex] | [latex]6\times12 = \bf{72}[/latex] |
and you can keep going as high as you want.
The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, and so on. & The multiples of 6 are 6, 12, 18, 24, 30, 36, and so on.
Exercise 9
List the first ten multiples of each number. This chart may be useful to you later.
- 2 Multiples 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
- 3
- 4
- 5
- 9
- 10
- 11
- 12
Answers to Exercise 9
- 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
- 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
- 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
- 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
- 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
- 11, 22, 33, 44, 55, 66, 77, 88, 99, 110
- 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
Example G
What is the least common multiple (LCM) of 3 and 5?
- Multiples:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
- Multiples of 5: 5, 10, 15, 20, 25, 30…
The least common multiple of 3 and 5 is 15.
Example H
What is the LCM of 3 and 4?
- Multiples:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32 ….
- The least common multiple of 3 and 4 is 12.
Example I
What is the LCM of 4 and 8?
- Multiples:
- Multiples of 4: 4, 8, 12, 16, 20…
- Multiples of 8: 8, 16, 24, 32, 40…
- The least common multiple of 4 and 8 is 8.
- LCM of 3 and 6 is 6
- LCM of 2 and 4 is 4
- LCM of 5 and 15 is 15
Exercise 10
Find the Least Common Multiple of these pairs of numbers. Use your chart from Exercise 9 to help you. You may want to add the multiples of other numbers to that chart.
- 3, 6
- 2, 5
- 12, 3
- 6, 12
- 5, 4
- 4, 8
- 8, 16
- 4, 7
- 25, 5
- 2, 9
- 6, 10
- 8, 12
Answers Exercise 10
- 6
- 10
- 12
- 12
- 20
- 8
- 16
- 28
- 25
- 18
- 30
- 24
Now that you know how to find an LCM, you can apply this knowledge to adding and subtracting fractions.
Least Common Denominator (LCD)
To find the Least Common Denominator of common fractions: find the least common multiple of the denominators.
Example J
What is the least common denominator of [latex]\dfrac{1}{2}[/latex] and [latex]\dfrac{3}{4}[/latex]?
The denominators are 2 and 4.
The least common multiple of 2 and 4 is 4.
So the least common denominator (LCD) for [latex]\dfrac{1}{2}[/latex] and [latex]\dfrac{3}{4}[/latex] is 4.
Example K
What is the LCD of [latex]\dfrac{3}{4}[/latex] and [latex]\dfrac{2}{3}[/latex]?
The denominators are 4 and 3.
The least common multiple of 4 and 3 is 12.
So the least common denominator for [latex]\dfrac{3}{4}[/latex] and [latex]\dfrac{2}{3}[/latex] is 12.
Exercise 11
Find the Least Common Denominator (LCD) for these pairs of fractions.
| Fractions | Denominators | Least Common Denominators | |
|---|---|---|---|
| a) | [latex]\dfrac{5}{8}[/latex], [latex]\dfrac{2}{3}[/latex] | 8, 3 | 24 |
| b) | [latex]\dfrac{1}{5}[/latex], [latex]\dfrac{1}{10}[/latex] | ||
| c) | [latex]\dfrac{1}{3}[/latex], [latex]\dfrac{3}{4}[/latex] | ||
| d) | [latex]\dfrac{2}{3}[/latex], [latex]\dfrac{1}{5}[/latex] | ||
| e) | [latex]\dfrac{5}{8}[/latex], [latex]\dfrac{1}{16}[/latex] |
Answers to Exercise 11 (only least common denominator is given)
- 10
- 12
- 15
- 16
You know how to find the least common denominator (LCD). The next step is to make equivalent fractions using the LCD.
Step 1: Find the least common denominator.
[latex]\begin{array}{rr}&\dfrac{3}{4}\\+&\dfrac{1}{3}\\ \hline\end{array}[/latex]
LCD of 4 and 3 is 12.
Step 2: Write an = sign after each fraction, followed by the common denominator.
[latex]\begin{array}{rrrr}&\dfrac{3}{4}=\dfrac{ }{12}\\+&\dfrac{1}{3} = \dfrac{ }{12}\\ \hline\end{array}[/latex]
Step 3: Rename the fractions as equivalent fractions with the LCD.
[latex]\dfrac{3}{4}[/latex] = [latex]\dfrac{ }{12}[/latex]
4 times what = 12?
4 × 3 = 12
If the denominator was multiplied by 3, the numerator must be multiplied by 3.
[latex]\dfrac{3}{4}[/latex] [latex]\dfrac{×3}{×3}[/latex] = [latex]\dfrac{9}{12}[/latex]
Now rename the other fraction.
[latex]\dfrac{1}{3}[/latex] = [latex]\dfrac{ }{12}[/latex]
3 times what = 12?
[latex]3\times 4 = 12[/latex]
If this denominator was multiplied by 4, this numerator must be multiplied by 4.
[latex]\dfrac{1}{3}[/latex] [latex]\dfrac{×4}{×4}[/latex] = [latex]\dfrac{4}{12}[/latex]
Now rename the other fraction.
Step 4: The question now looks like this and can be added.
[latex]\begin{array}{rrrr}&\dfrac{3}{4}&=&\dfrac{9}{12}\\ +&\dfrac{1}{3} &= &\dfrac{4}{12}\\ \hline \\ & \dfrac{13}{12}&=& 1\dfrac{1}{12}\end{array}[/latex]
Example L
[latex]\dfrac{1}{4} + \dfrac{3}{8}[/latex] =
Step 1 and 2: Find the least common denominator
[latex]\begin{array}{ll}&\dfrac{1}{4} = \dfrac{ }{8}\\+&\dfrac{3}{8}= \dfrac{ }{8}\\ \hline\end{array}[/latex]
Step 3: Rename as equivalent fractions
[latex]\begin{array}{ll}&\dfrac{1}{4}\left(\dfrac{\times2}{\times2}\right) = \dfrac{2}{8}\\+&\dfrac{3}{8}\left(\dfrac{\times1}{\times1}\right)= \dfrac{3}{8}\\ \hline\end{array}[/latex]
Step 4: Add and simplify the answer.
[latex]\begin{array}{lll}&\dfrac{1}{4}\left(\dfrac{×2}{×2}\right) = &\dfrac{2}{8}\\+&\dfrac{3}{8}\left(\dfrac{×1}{×1}\right)= &\dfrac{3}{8}\\ \hline&&\dfrac{5}{6}\end{array}[/latex]
Exercise 12
Add these common fractions. Express the answer in lowest terms.
- [latex]\begin{array}{rr}&\dfrac{1}{2}\left(\dfrac{×4}{×4}\right) =&\dfrac{4}{8}\\+&\dfrac{3}{8}\left(\dfrac{×1}{×1}\right)= &\dfrac{3}{8}\\ \hline&&\dfrac{7}{8}\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{1}{4}\left(\dfrac{×2}{×2}\right) =&\dfrac{2}{8}\\+&\dfrac{3}{8}\left(\dfrac{×1}{×1}\right)= &\dfrac{3}{8}\\ \hline&&\dfrac{5}{8}\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{1}{5}\\+&\dfrac{1}{10}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{5}{16}\\+&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{1}{3}\\+&\dfrac{7}{12}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{2}{3}\\+&\dfrac{1}{6}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{3}{10}\\ +&\dfrac{2}{5}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{1}{12}\\ +&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
Answers to Exercise 12
- [latex]\tfrac{3}{10}[/latex]
- [latex]\tfrac{9}{16}[/latex]
- [latex]\tfrac{11}{12}[/latex]
- [latex]\tfrac{5}{6}[/latex]
- [latex]\tfrac{7}{10}[/latex]
- [latex]\tfrac{1}{3}[/latex]
How did you do? If you are struggling with this process, speak to your instructor for help.
Exercise 13
More practice. Do only as many as you think you need.
- [latex]\begin{array}{rrr}&\dfrac{2}{3}\left(\dfrac{×4}{×4}\right) &=\dfrac{8}{12}\\&\dfrac{1}{2}\left(\dfrac{×6}{×6}\right)&=\dfrac{6}{12}\\+&\dfrac{3}{4}\left(\dfrac{×3}{×3}\right)& = \dfrac{9}{12}\\ \hline&&\dfrac{23}{12}&=1\dfrac{11}{12}\end{array}[/latex]
- [latex]\begin{array}{rrr}&\dfrac{5}{24}\left(\dfrac{×1}{×1}\right)& =\dfrac{5}{24}\\&\dfrac{1}{3}\left(\dfrac{×8}{×8}\right)&= \dfrac{8}{24}\\+&\dfrac{3}{8}\left(\dfrac{×3}{×3}\right)&= \dfrac{9}{24}\\ \hline&&\dfrac{22}{24}&=\dfrac{11}{12}\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{5}{12}\\&\dfrac{5}{6}\\+&\dfrac{3}{4}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{3}{10}\\&\dfrac{3}{4}\\+&\dfrac{4}{5}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{1}{2}\\&\dfrac{2}{5}\\+&\dfrac{7}{10}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{5}{6}\\&\dfrac{3}{4}\\+&\dfrac{1}{3}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{7}{16}\\+&\dfrac{3}{4}\\ \hline\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{4}{5}\\+&\dfrac{1}{3}\\ \hline\end{array}[/latex]
Answers to Exercise 13
- 2
- [latex]1\tfrac{17}{20}[/latex]
- [latex]1\tfrac{3}{5}[/latex]
- [latex]1\tfrac{11}{12}[/latex]
- [latex]1\tfrac{3}{16}[/latex]
- [latex]1\tfrac{2}{15}[/latex]
Addition questions are often written with the fractions side by side instead of one fraction above the other. For example:
[latex]\dfrac{2}{3}[/latex] + [latex]\dfrac{5}{8}[/latex] =
You may solve as shown in this example or rewrite the question with the fractions one above the other.
[latex]\dfrac{2}{3} + \dfrac{5}{8} = \dfrac{2}{3}\dfrac{×8}{×8} + \dfrac{5}{8}\dfrac{×3}{×3}= \dfrac{16}{24}+ \dfrac{15}{24}=\dfrac{31}{24}= 1 \dfrac{7}{24}[/latex]
or
[latex]\begin{array}{rrr}&\dfrac{2}{3}\left(\dfrac{×8}{×8}\right) &=\dfrac{16}{24}\\&\dfrac{5}{8}\left(\dfrac{×3}{×3}\right)&=\dfrac{15}{24}\\ \hline&&\dfrac{31}{24}&=1\dfrac{7}{24}\end{array}[/latex]
Exercise 14
Find the sum. Do enough questions to be confident in your skill.
- [latex]\begin{array}{rr} \\ \dfrac{1}{2} + \dfrac{1}{6} = &\\ \dfrac{1}{2}\left( \dfrac{\times 3}{\times 3}\right) + \dfrac{1}{6} = &\\ \dfrac{3}{6} + \dfrac{1}{6} = &\dfrac{4}{6} = \dfrac{2}{3} \end{array}[/latex]
- [latex]\dfrac{1}{4} + \dfrac{7}{8}[/latex] =
- [latex]\dfrac{1}{5} + \dfrac{3}{5}[/latex] =
- [latex]\dfrac{1}{12}+\dfrac{2}{3}[/latex] =
- [latex]\dfrac{1}{3} + \dfrac{2}{3}[/latex] =
- [latex]\dfrac{1}{6} + \dfrac{3}{8}[/latex] =
- [latex]\dfrac{3}{4} + \dfrac{1}{2}[/latex] =
- [latex]\dfrac{1}{3} + \dfrac{5}{8}[/latex] =
Answers to Exercise 14
- [latex]1\tfrac{1}{8}[/latex]
- [latex]\tfrac{4}{5}[/latex]
- [latex]\tfrac{3}{4}[/latex]
- 1
- [latex]\tfrac{13}{24}[/latex]
- [latex]1\tfrac{1}{4}[/latex]
- [latex]\tfrac{23}{24}[/latex]
You already know how to add mixed numbers which have the same (like) denominators.
To add mixed numbers with different denominators, you must:
- Find the least common denominator (LCD) for the fractions.
- Rename the fractions as equivalent fractions using the LCD
- Be sure to bring the whole number across the equal sign when you rename.
- Add the fractions.
- Add the whole numbers.
- Simplify the answer.
- Remember that if the sum of the fractions is an improper fraction, you must rename it as a mixed number that is added to the whole number in your answer.
Example M
[latex]\begin{array}{rr}&3\dfrac{3}{4}\left(\dfrac{\times5}{\times5}\right)=3\dfrac{15}{20} \\ +&6\dfrac{1}{5}\left(\dfrac{\times 4}{\times 4}\right)=6\dfrac{4}{20} \\ \hline \\ & =9\dfrac{19}{20}\end{array}[/latex]
Example N
[latex]\begin{array}{rr}&3\dfrac{3}{4}\left(\dfrac{\times3}{\times3}\right)=3\dfrac{9}{12} \\ &8\dfrac{2}{3}\left(\dfrac{\times 4}{\times 4}\right)=8\dfrac{8}{12} \\ +& 2 \dfrac{1}{2} \left(\dfrac{\times 6}{\times 6}\right) = 2 \dfrac{6}{12} \\ \hline \\ & =13\dfrac{23}{12}\end{array}[/latex]
[latex]\dfrac{23}{12}[/latex] is an improper fraction, so we simplify it: [latex]\dfrac{23}{12} = 1 \dfrac{11}{12}[/latex]
Therefore, the answer becomes:
[latex]13 \dfrac{23}{12} = 13 + 1 \dfrac{11}{12} = 14 \dfrac{11}{12}[/latex]
Exercise 15
Add. Express the sums in lowest terms.
- [latex]\begin{array}{rrrrr}&1\dfrac{3}{8}\left(\dfrac{\times1}{\times1}\right)&=&1\dfrac{3}{8}&\\+&1\dfrac{1}{4}\left(\dfrac{\times2}{\times2}\right)&=&1\dfrac{2}{8}&\\\hline&&&2\dfrac{5}{8} \end{array}[/latex]
- [latex]\begin{array}{rr}&3\dfrac{1}{5}\\+&2\dfrac{3}{10}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&6\dfrac{2}{15}\\+&1\dfrac{3}{10}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&8\dfrac{1}{4}\\+&4\dfrac{1}{3}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&5\dfrac{2}{3}\\+&6\dfrac{1}{4}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&116\dfrac{5}{8}\\+&9\dfrac{1}{24}\\ \hline&\end{array}[/latex]
Answers to Exercise 15
- [latex]5\tfrac{1}{2}[/latex]
- [latex]7\tfrac{13}{30}[/latex]
- [latex]12\tfrac{7}{12}[/latex]
- [latex]11\tfrac{11}{12}[/latex]
- [latex]125\tfrac{2}{3}[/latex]
Exercise 16
Add. Express the sums in lowest terms.
- [latex]\begin{array}{rrrrr}&4\dfrac{1}{2}\left(\dfrac{\times6}{\times6}\right)&=&4\dfrac{6}{12}&\\+&2\dfrac{1}{3}\left(\dfrac{\times4}{\times4}\right)&=&2\dfrac{4}{12}&\\\hline&&&6\dfrac{10}{12}&=6\dfrac{5}{6}\end{array}[/latex]
- [latex]\begin{array}{rr}&3\dfrac{2}{3}\\+&1\dfrac{1}{2}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&6\dfrac{1}{2}\\+&4\dfrac{1}{4}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&2\dfrac{1}{8}\\+&4\dfrac{3}{16}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&2\dfrac{1}{5}\\+&3\dfrac{2}{3}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&3\dfrac{3}{8}\\&2\dfrac{3}{4}\\+&1\dfrac{1}{2}\\\hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&4\dfrac{3}{4}\\&2\dfrac{1}{5}\\+&4\dfrac{1}{2}\\ \hline&\end{array}[/latex]
Answers to Exercise 16
- [latex]5\tfrac{1}{6}[/latex]
- [latex]10\tfrac{3}{4}[/latex]
- [latex]6\tfrac{5}{16}[/latex]
- [latex]5\tfrac{13}{15}[/latex]
- [latex]7\tfrac{5}{8}[/latex]
- [latex]11\tfrac{9}{20}[/latex]
Problems Using Addition of Common Fractions
Exercise 17
Solve these problems.
- The bathroom shelf is crowded with hand lotion bottles, each with a little lotion left inside. Everyone always likes to try the new bottle before the old one is emptied! One bottle is [latex]\tfrac{1}{3}[/latex] full, another is [latex]\tfrac{1}{4}[/latex] full, one is only [latex]\tfrac{1}{8}[/latex] full and one is still [latex]\tfrac{1}{2}[/latex] full. How much lotion is in the bottles altogether?
- Sometimes Joan thinks she will go crazy when she packs the lunches for her family. Little Sarah has decided she only wants [latex]\tfrac{3}{4}[/latex] of a sandwich, Megan wants [latex]\tfrac{1}{4}[/latex] of a sandwich, Joan’s husband takes [latex]1\tfrac{1}{2}[/latex] sandwiches, and their son, who does heavy work, takes 3 sandwiches! How many sandwiches does Joan make?
- Dave paid the babysitter for the week. The sitter worked [latex]3\tfrac{3}{4}[/latex] hours on Monday, [latex]4\tfrac{1}{4}[/latex] hours on Tuesday and [latex]6\tfrac{1}{2}[/latex] hours on Friday. How many hours did the babysitter work looking after Dave’s children that week?
- Quite a lot of watermelon was left after the watermelon-eating contest: [latex]1\tfrac{1}{2}[/latex] watermelons on one table, [latex]2\tfrac{3}{4}[/latex] of a watermelon on another table and [latex]\tfrac{5}{8}[/latex] of a watermelon on the third table. The organizers want to know exactly how much was left over so they will not buy so much next year. Calculate the amount of watermelon left over.
- Jeanette has a novel to read for English. She read [latex]\tfrac{1}{2}[/latex] of the book on the weekend, only had time to read [latex]\tfrac{1}{8}[/latex] of the book on Monday and another [latex]\tfrac{1}{4}[/latex] on Wednesday. How much of the book has she read?
- Dion walks around this route each day for exercise. How far does he walk each day? Is this a perimeter or area question?

- How many metres of baseboard are needed for a rectangular room [latex]4\tfrac{1}{2}[/latex] m by [latex]3\tfrac{1}{5}[/latex]m? Deduct 1 m for the doorway. (TIP: Draw a picture)
- Sana is going to frame a large piece of art with a wooden frame. The art piece is [latex]1\tfrac{1}{10}[/latex] m by [latex]\tfrac{3}{5}[/latex] m. How much framing material should she buy?
- Find the perimeter of the following figure.
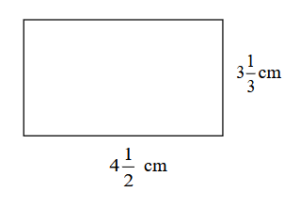
- Find the perimeter of a picture frame if one side is [latex]12 \frac{1}{10}[/latex] cm and the other side measures [latex]14\frac{1}{5}[/latex] cm.
- Find the perimeter of this triangle.
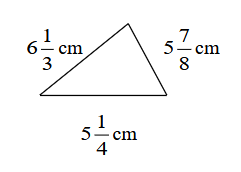
Answers to Exercise 17
- [latex]1\tfrac{5}{24}[/latex] bottles total
- 5 ½ sandwiches
- 14 ½ hours
- [latex]4\tfrac{7}{8}[/latex] watermelons
- [latex]\tfrac{7}{8}[/latex] of the book
- He walks [latex]4\tfrac{1}{3}[/latex] km each day, perimeter
- [latex]14 \frac{2}{5}\text{ m }[/latex]of material
- [latex]3\frac{2}{5}\text{ m }[/latex]of material
- [latex]15\frac{2}{3}\text{ cm}[/latex]
- [latex]52\frac{3}{5}\text{ cm}[/latex]
- [latex]17\frac{11}{24}\text{ cm}[/latex]
Topic A: Self-Test
Mark /14 Aim 11/14
- Add and express the answers in lowest terms (6 marks).
- [latex]\begin{array}{rr}&\dfrac{1}{4}\\+&\dfrac{3}{4}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&1\dfrac{3}{5}\\+&3\dfrac{4}{5}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&\dfrac{3}{8}\\+&\dfrac{3}{4}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&2\dfrac{1}{6}\\+&3\dfrac{5}{12}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&6\dfrac{3}{4}\\+&2\dfrac{1}{2}\\ \hline&\end{array}[/latex]
- [latex]\begin{array}{rr}&6\dfrac{7}{8}\\+&9\dfrac{1}{3}\\ \hline&\end{array}[/latex]
- Word Problems (8 marks).
- The flight from Vancouver to Sandspit took [latex]1\dfrac{1}{4}[/latex] hours. The wait in Sandspit was [latex]1\dfrac{1}{2}[/latex] hours and the flight from there to Ketchican, Alaska was [latex]\dfrac{3}{4}[/latex] of an hour. How long did it take to make the trip from Vancouver, BC to Ketchican, Alaska?
- Dave built [latex]\dfrac{1}{8}[/latex] of the fence around his house on Monday, [latex]\dfrac{1}{4}[/latex] of it on Tuesday and another [latex]\dfrac{1}{4}[/latex] on Wednesday. How much of the fence has he built?
- John bought snacks in bulk for the class party. His items weighed [latex]\dfrac{2}{5}[/latex] kg of chips, [latex]\dfrac{3}{5}[/latex] kg of peanuts, [latex]\dfrac{1}{2}[/latex] kg of cheese and [latex]1\dfrac{1}{4}[/latex] kg of fresh veggies. How much did all his snacks weigh?
- Clarence is making a frame for his favourite photo. The frame needs to be [latex]\dfrac{1}{8}[/latex] m by [latex]\dfrac{5}{6}[/latex] m. How much material should he buy?
Answers to Topic A Self-Test
-
- 1
- [latex]5\tfrac{2}{5}[/latex]
- [latex]1\tfrac{1}{8}[/latex]
- [latex]5\tfrac{7}{12}[/latex]
- [latex]9\tfrac{1}{4}[/latex]
- [latex]16\tfrac{5}{24}[/latex]
-
- [latex]3\tfrac{1}{2}[/latex] hr
- [latex]\tfrac{5}{8}[/latex] of the fence
- [latex]2 \tfrac{3}{4}[/latex] kg of food
- [latex]1 \tfrac{11}{12}[/latex] m of material
The result of an addition question, the answer to an addition question.
A common fraction with a value less than one.
The numbers to be added together in an addition question. In 3 + 5 = 8, the addends are 3 and 5.
The bottom number in a common fraction; the denominator tells into how many equal parts the whole thing has been divided.

