Unit 3: Multiplying & Dividing Fractions
Topic B: Dividing Common Fractions
Think over what you know about dividing:
When we divide, we take the total amount and separate (divide it) into equal parts or groups.
Remember:

Example A
[latex]8 \div 4 =[/latex]
- The total amount is 8.
- The divisor is 4. How many groups of 4 are in 8? Yes, 2.
- [latex]8 \div 4 = 2[/latex]
Example B
[latex]3 \div \dfrac{1}{2}=[/latex]
- The total amount is 3.
- The divisor is [latex]\dfrac{1}{2}[/latex]. How many times does [latex]\dfrac{1}{2}[/latex] go into 3?
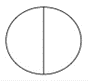


- There are 6 halves.
- [latex]3 \div \dfrac{1}{2}=6[/latex]
Example C
[latex]2÷\dfrac{2}{3}[/latex]
- The total amount is 2.
- The divisor is [latex]\dfrac{2}{3}[/latex]. How many times does [latex]\dfrac{2}{3}[/latex] go into 2?
- Use different colours to shade in each group of two that you can find.
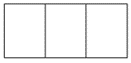

- [latex]2 ÷ \dfrac{2}{3} = 3[/latex]
Example D
[latex]1÷\dfrac{1}{4}[/latex]
- The total amount is 1. Divisor is [latex]\dfrac{1}{4}[/latex]
- How many [latex]\dfrac{1}{4}[/latex]s in 1?
- Draw a shape. Divide it into quarters. How many [latex]\dfrac{1}{4}\text{s}[/latex] are there?
- There are 4 quarters.
- [latex]1÷\dfrac{1}{4} = 4[/latex]
Example E
[latex]3÷\dfrac{3}{8} =[/latex]
- How many [latex]\dfrac{3}{8}[/latex] in 3.
- Use different colors to shade in each group of 3 that you can find.
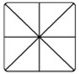


- Did you find 8 groups of [latex]\dfrac{3}{8}[/latex]? [latex]3÷\dfrac{3}{8} = 8[/latex]
Division of fractions by a fraction is difficult to picture, probably because it is not often used in everyday life. Here are some everyday examples for you to think about.
- You have half a dollar. Someone asks you to change it for quarters. How many quarters are there in half a dollar?
[latex]\dfrac{1}{2}\div\dfrac{1}{4}=2[/latex] 2 quarters in one half dollar - It takes [latex]\tfrac{1}{4}[/latex] hour to solve a math problem. How many problems can you solve in [latex]\tfrac{3}{4}[/latex] of an hour?
[latex]\dfrac{3}{4}\div\dfrac{1}{4}=3[/latex] 3 problems in one [latex]\tfrac{3}{4}[/latex] of an hour
Reciprocals
Dividing by a number is the same as multiplying by its reciprocal. We use reciprocals when we divide fractions. Two numbers are reciprocals if they have a product of 1.
To find the reciprocal of a fraction, turn the fraction upside down (flip it over). This is called “inverting the fraction.”
| Fraction | Reciprocal |
|---|---|
| [latex]\dfrac{1}{2}[/latex] | [latex]\dfrac{2}{1}[/latex] |
| [latex]\dfrac{3}{4}[/latex] | [latex]\dfrac{4}{3}[/latex] |
| [latex]\dfrac{7}{8}[/latex] | [latex]\dfrac{8}{7}[/latex] |
| [latex]\dfrac{2}{3}[/latex] | [latex]\dfrac{3}{2}[/latex] |
| [latex]\dfrac{1}{4}[/latex] | [latex]\dfrac{4}{1}[/latex] |
To find the reciprocal of a whole number:
- Rename the whole number as a fraction with a denominator of 1.
- Invert the fraction
- Check the reciprocal by multiplying the fraction by the reciprocal. The product will be one.
| Whole Number | Fraction | Reciprocal | Check |
|---|---|---|---|
| [latex]3[/latex] | [latex]\dfrac{3}{1}[/latex] | [latex]\dfrac{1}{3}[/latex] | [latex]\dfrac{\cancel{3}1}{1}\times\dfrac{1}{\cancel{3}1}=1[/latex] |
| [latex]6[/latex] | [latex]\dfrac{6}{1}[/latex] | [latex]\dfrac{1}{6}[/latex] | [latex]\dfrac{\cancel{6}1}{1}\times\dfrac{1}{\cancel{6}1}=1[/latex] |
| [latex]10[/latex] | [latex]\dfrac{10}{1}[/latex] | [latex]\dfrac{1}{10}[/latex] | [latex]\dfrac{\cancel{10}1}{1}\times\dfrac{1}{\cancel{10}1}=1[/latex] |
To find the reciprocal of a mixed number
- Rename the mixed number as an improper fraction.
- Invert the fraction
| Mixed Number | Fraction | Reciprocal | Check |
|---|---|---|---|
| [latex]1\dfrac{1}{2}=[/latex] | [latex]\dfrac{3}{2}[/latex] | [latex]\dfrac{2}{3}[/latex] | [latex]\dfrac{\cancel{3}1}{\cancel{2}1}\times\dfrac{\cancel{2}1}{\cancel{3}1}[/latex]=[latex]\dfrac{6}{6}=1[/latex] |
| [latex]2\dfrac{1}{3}[/latex] | [latex]\dfrac{7}{3}[/latex] | [latex]\dfrac{3}{7}[/latex] | [latex]\dfrac{\cancel{7}1}{\cancel{3}1}\times\dfrac{\cancel{3}1}{\cancel{7}1}[/latex][latex]\dfrac{1}{1}[/latex]=1 |
| [latex]4\dfrac{3}{8}[/latex] | [latex]\dfrac{35}{8}[/latex] | [latex]\dfrac{8}{35}[/latex] | [latex]\dfrac{\cancel{35}1}{\cancel{8}1}\times\dfrac{\cancel{8}1}{\cancel{35}1}[/latex]=1 |
Exercise 1
Write the reciprocal of these numbers.
- [latex]\dfrac{2}{5}[/latex] The reciprocal is [latex]\dfrac{5}{2}[/latex]
- [latex]\dfrac{5}{8}[/latex]
- [latex]\dfrac{1}{2}[/latex]
- [latex]5=\dfrac{5}{1}[/latex] The reciprocal is [latex]\dfrac{1}{5}[/latex]
- [latex]9[/latex]
- [latex]2[/latex]
- [latex]2\dfrac{1}{2}=\dfrac{5}{2}[/latex] The reciprocal is [latex]\dfrac{2}{5}[/latex]
- [latex]1\dfrac{1}{4}[/latex]
- [latex]8\dfrac{1}{3}[/latex]
Answers to Exercise 1
- [latex]\dfrac{5}{2}[/latex]
- [latex]\dfrac{8}{5}[/latex]
- 2
- [latex]\dfrac{1}{5}[/latex]
- [latex]\dfrac{1}{9}[/latex]
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{2}{5}[/latex]
- [latex]\dfrac{4}{5}[/latex]
- [latex]\dfrac{3}{25}[/latex]
Multiplying by the Reciprocal
To divide fractions, multiply by the reciprocal of the divisor.
- Step 1: Rewrite the division question.
- Rename all mixed numbers as improper fractions.
- Give any whole numbers a denominator of 1
- Step 2: Change the ÷ sign to a × sign.
- Invert (turn upside down) the divisor to make the reciprocal.
- Remember the divisor is always the number after the sign.
- Step 3: Simplify (cancel) and then multiply to find the answer.
- Step 4: Write the answer in lowest terms.
Example F
[latex]\dfrac{3}{4}\div\dfrac{1}{2}=[/latex]
Step 1: No whole numbers or mixed numbers.
Step 2: [latex]\dfrac{3}{4}\div\dfrac{1}{2}=\dfrac{3}{4}\times\dfrac{2}{1}=[/latex]
Step 3 and 4: [latex]\dfrac{3}{\cancel{4}2}\times\dfrac{\cancel{2}1}{1}=\dfrac{3}{2} = 1\dfrac{1}{2}[/latex]
Example G
[latex]\dfrac{7}{8}\div\dfrac{1}{4}=[/latex]
Step 1: No whole numbers or mixed numbers.
Step 2: [latex]\dfrac{7}{8}\div\dfrac{1}{4}=\dfrac{7}{8}\times\dfrac{4}{1}=[/latex]
Step 3 and 4: [latex]\dfrac{7}{\cancel{8}2}\times\dfrac{\cancel{4}1}{1}=\dfrac{7}{2} = 3\dfrac{1}{2}[/latex]
Example H
[latex]5\div\dfrac{2}{3}=[/latex]
Step 1: [latex]5\div\dfrac{2}{3}= \dfrac{5}{1}\div\dfrac{2}{3}=[/latex]
Step 2: [latex]\dfrac{5}{1}\times\dfrac{3}{2}=[/latex]
Step 3 and 4: [latex]\dfrac{5}{1}\times\dfrac{3}{2}=\dfrac{15}{2}=7\dfrac{1}{2}[/latex]
Example I
[latex]3\dfrac{1}{2}\div2\dfrac{3}{4}=[/latex]
Step 1: [latex]3\dfrac{1}{2}\div2\dfrac{3}{4}=\dfrac{7}{2}\div\dfrac{11}{4}[/latex]
Step 2: [latex]\dfrac{7}{2}\times\dfrac{4}{11}=[/latex]
Step 3 and 4: [latex]\dfrac{7}{\cancel{2}1}\times\dfrac{\cancel{4}2}{11}=\dfrac{14}{11}=1 \dfrac{3}{11}[/latex]
Exercise 2
Divide these fractions using the steps you have just learned.
- [latex]\dfrac{4}{9}\div 4 =[/latex]
[latex]\dfrac{4}{9} \div \dfrac{4}{1} = \dfrac{4}{9} \times \dfrac{1}{4} =[/latex]
[latex]\dfrac{\cancel{4}1}{9} \times \dfrac{1}{\cancel{4}1} = \dfrac{1}{9}[/latex] - [latex]\dfrac{7}{2}\div\dfrac{3}{5}=[/latex]
- [latex]\dfrac{5}{8}\div\dfrac{7}{16}=[/latex]
- [latex]\dfrac{2}{3}\div\dfrac{8}{9}=[/latex]
- [latex]\dfrac{1}{5}\div\dfrac{1}{2}=[/latex]
- [latex]\dfrac{5}{6}\div\dfrac{5}{3}=[/latex]
- [latex]\dfrac{1}{3}\div\dfrac{3}{8}=[/latex]
- [latex]\dfrac{6}{7}\div\dfrac{1}{6}=[/latex]
Answers to Exercise 2
- [latex]5\dfrac{5}{6}[/latex]
- [latex]1\dfrac{3}{7}[/latex]
- [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{2}{5}[/latex]
- [latex]\dfrac{1}{2}[/latex]
- [latex]\dfrac{8}{9}[/latex]
- [latex]5\dfrac{1}{7}[/latex]
Exercise 3
If you need more practice, try a few more of these division questions. If you are not having any trouble, go on to Exercise Four, which has mixed numbers in it.
Divide these fractions using the steps you have just learned.
- [latex]\dfrac{1}{2}\div\dfrac{1}{8}=[/latex]
[latex]\dfrac{1}{2} \times \dfrac{8}{1} = \dfrac{1}{\cancel{2}1} \times \dfrac{\cancel{8}4}{1} = \dfrac{4}{1} = 4[/latex] - [latex]\dfrac{8}{9}\div\dfrac{3}{2}=[/latex]
- [latex]\dfrac{3}{4}\div\dfrac{3}{4}=[/latex]
- [latex]\dfrac{5}{6}\div\dfrac{3}{3}=[/latex]
- [latex]\dfrac{1}{3}\div\dfrac{3}{4}=[/latex]
- [latex]\dfrac{2}{3}\div\dfrac{1}{2}=[/latex]
Answers to Exercise 3
- [latex]\dfrac{16}{27}[/latex]
- 1
- [latex]\dfrac{5}{6}[/latex]
- [latex]\dfrac{4}{9}[/latex]
- [latex]1\dfrac{1}{3}=\dfrac{4}{3}[/latex]
Exercise 4
More practice: You might want to save some of this exercise to do as review before a test.
- [latex]8\div\dfrac{1}{2}=[/latex]
- [latex]2\dfrac{2}{5}\div\dfrac{1}{8}=[/latex]
- [latex]\dfrac{1}{6}\div\dfrac{1}{5}=[/latex]
- [latex]\dfrac{1}{8}\div\dfrac{1}{5}=[/latex]
- [latex]\dfrac{3}{5}\div\dfrac{1}{4}=[/latex]
- [latex]2\dfrac{4}{5}\div\dfrac{1}{5}=[/latex]
- [latex]\dfrac{2}{5}\div\dfrac{1}{2}=[/latex]
- [latex]\dfrac{1}{4}\div\dfrac{2}{3}=[/latex]
- [latex]2\dfrac{3}{4}\div1\dfrac{7}{8}=[/latex]
- [latex]5\dfrac{1}{10}\div3\dfrac{3}{10}=[/latex]
- [latex]1\dfrac{5}{9}\div3\dfrac{1}{3}=[/latex]
- [latex]\dfrac{1}{2}\div\dfrac{3}{8}=[/latex]
Answers to Exercise 4
- 16
- [latex]19\dfrac{1}{5}[/latex]
- [latex]\dfrac{5}{6}[/latex]
- [latex]\dfrac{5}{8}[/latex]
- [latex]2\dfrac{2}{5}[/latex]
- 14
- [latex]\dfrac{4}{5}[/latex]
- [latex]\dfrac{3}{8}[/latex]
- [latex]1\dfrac{7}{15}[/latex]
- [latex]1\dfrac{6}{11}[/latex]
- [latex]\dfrac{7}{15}[/latex]
- [latex]1\dfrac{1}{3}[/latex]
Problems Which Use Division of Common Fractions
Look for word patterns and key words in the division problems. Thinking about the problems using whole numbers instead of fractions may sometimes help you to recognize the division pattern. Start your division equation with the dividend. The dividend is the total.
These key words often point to division:
- separated split cut shared
- What is cost per…? unit pricing
- What is distance per…? average (speed, cost, weight, time)
Exercise 5
- Every fall three friends get together to make antipasto. Last year they filled [latex]4\tfrac{1}{2}[/latex] ice cream buckets with antipasto and then shared it equally. How many buckets of antipasto did each person get?
- A pick-up truck load of split wood is [latex]\tfrac{1}{2}[/latex] cord of wood. If you shared a full truck load of wood with a neighbour, how much of a cord of firewood would you each get?
- The distance from Trail, BC to Vancouver, BC is 640 km via the Crowsnest Highway. The trip can be made in [latex]7\tfrac{1}{2}[/latex] hours in good weather. What average speed must be maintained?
- The sweater that Janet is knitting has a complicated pattern. It takes her [latex]3\tfrac{3}{4}[/latex] hours to finish 15 rows. How long does each row take?
- Marian had [latex]\tfrac{12}{3}[/latex] lemon pies left which she wanted to share equally amongst 10 people. How much of a pie will each person be given?
- Jack wants to cut his piece of trim for his square windows into 4 equal parts. The trim is [latex]2\tfrac{2}{5}[/latex] metres long. What will the measurement be of each piece?
- Tony is sewing 3 identical pairs of pants for his son’s dance performance. He bought 2⅓ metres of material. He uses up all of the material; how much material was used for each pair of pants?
- Joy has a [latex]7\tfrac{1}{4}[/latex] m long stick. She needs to split it into [latex]\tfrac{1}{3}[/latex] m pieces. How many pieces can she get? (Remember: your answer will be given with the unit of ‘pieces’ not metres!)
Answers to Exercise 5
- [latex]1\dfrac{1}{2}[/latex] buckets
- [latex]\dfrac{1}{4}[/latex] cord
- [latex]85\dfrac{1}{3}[/latex] km/h (85.3 km/h)
- [latex]\dfrac{1}{4}[/latex] hour or 15 minutes
- [latex]\dfrac{1}{6}[/latex] pie
- Each piece is [latex]\dfrac{3}{5}[/latex] metres long.
- He uses [latex]\dfrac{7}{9}[/latex] metre for each pair.
- She will get 21 pieces.
Topic B: Self-Test
Mark /10 Aim 8/10
- Divide and be sure the answers are in lowest terms. (8 marks)
- [latex]\dfrac{3}{4}\div\dfrac{1}{4}=[/latex]
- [latex]\dfrac{1}{4}\div1\dfrac{1}{4}=[/latex]
- [latex]\dfrac{5}{8}\div\dfrac{15}{16}=[/latex]
- [latex]6\div\dfrac{7}{9}=[/latex]
- [latex]\dfrac{5}{11}\div11=[/latex]
- [latex]9\dfrac{3}{4}\div2=[/latex]
- [latex]3\div\dfrac{1}{3}=[/latex]
- [latex]3\dfrac{3}{7}\div2\dfrac{5}{14}=[/latex]
- Word Problem (2 marks).
- Joe is a school janitor. It takes him [latex]\tfrac{3}{4}[/latex] of an hour to clean one classroom. How many classrooms does he clean in his [latex]7\tfrac{1}{2}[/latex] hour shift?
Answers to Topic B Self-Test
-
- 3
- [latex]\dfrac{1}{5}[/latex]
- [latex]\dfrac{2}{3}[/latex]
- [latex]7\dfrac{5}{7}[/latex]
- [latex]\dfrac{5}{121}[/latex]
- [latex]4\dfrac{7}{8}[/latex]
- 9
- [latex]1\dfrac{5}{11}[/latex]
-
- 10 classrooms
To separate into equal parts.
The number of groups or the quantity into which a number (the dividend) is to be separated.
A number, when multiplied by its reciprocal, equals 1. To find the reciprocal of a common fraction, invert it. ⅗ × ⁵⁄₃ = 1
The number or quantity to be divided; what you start with before you divide.
The price for a set amount. E.g., price per litre, price per gram.
Any fixed quantity, amount, distance or measure that is used as a standard. In mathematics, always identify the unit with which you are working. E.g., 3 km, 4 cups, 12 people, $76, 70 books, 545 g.

