Unit 4: Adding & Subtracting Common Fractions

Topic B: Subtracting Common Fractions

Good News!

There is only one new thing to learn in this topic. Everything else uses skills and knowledge you already have.

Let’s look at subtraction:

Example A

A rectangle divided in 5 equal parts. 4 parts and shaded and one unshaded.

The shaded part [latex]\left(\dfrac{4}{5}\right)[/latex] is the amount that you are starting with.

Now cross out (pretend you are taking away) 3 shaded parts [latex]\left(\dfrac{3}{5}\right)[/latex].

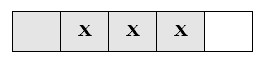
Repeat of rectangle divided in 5 equal parts. 4 of 5 shaded. One unshaded. Three 'x' es applied to 3 of the boxes.

Example B

Draw a pizza.

 

  • Slice it into 8 equal pieces.
  • Draw pieces of pineapple on 5 pieces.
  • What fraction of the pizza has pineapple?  [latex]\dfrac{5}{8}[/latex]
  • Cross out 2 pineapple pieces to show they have been eaten.
  • How much of the pineapple pizza is left?
  • [latex]\begin{array}{rrl}&\dfrac{5}{8}&\text{(amount you started with)}\\-&\dfrac{2}{8}&\text{(amount eaten, "taken away")}\\ \hline&\dfrac{3}{8}&\text {of the pizza is left with pineapple on it}\end{array}[/latex]

Common fractions must have the same denominator when you subtract one from the other. Subtract the numerators and keep the same denominators.

Exercise 1

Subtract to find the difference.

TIP: Express the difference in lowest terms.

  1. [latex]\begin{array}{rr}&\dfrac{3}{5}\\-&\dfrac{1}{5}\\\hline&\dfrac{2}{5}\end{array}[/latex]
  2. [latex]\begin{array}{rrrr}&\dfrac{7}{8} &&\\-&\dfrac{3}{8}&&\\ \hline &\dfrac{4}{8}&=&\dfrac{1}{2}\\ \end{array}[/latex]
  3. [latex]\begin{array}{rr}&\dfrac{2}{3}\\-&\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&\dfrac{5}{9}\\-&\dfrac{2}{9}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&\dfrac{6}{7}\\-&\dfrac{1}{7}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&\dfrac{3}{4}\\-&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&\dfrac{3}{2}\\-&\dfrac{1}{2}\\ \hline&\end{array}[/latex]

Answers to Exercise 1

  1. [latex]\dfrac{1}{3}[/latex]
  2. [latex]\dfrac{1}{3}[/latex]
  3. [latex]\dfrac{5}{7}[/latex]
  4. [latex]\dfrac{1}{2}[/latex]
  5. [latex]\dfrac{2}{2}[/latex] = 1

You know how to find the least common denominator (LCD) and to rewrite fractions in an equivalent form using the LCD.

You must use those skills when you wish to subtract fractions with different denominators.

Example C

[latex]\dfrac{4}{5}-\dfrac{3}{10} =[/latex]

Denominators are 5 and 10. The least common multiple is 10, so the least common denominator is 10.

[latex]\begin{array}{rrrr}&\dfrac{4}{5}\left(\dfrac{×2}{×2}\right) =&\dfrac{8}{10}&&\text{Write equivalent fractions using the LCD}\\ -&\dfrac{3}{10}=&\dfrac{3}{10} &&\text{Subtract the numerators}\\ \hline&=&\dfrac{5}{10}\left(\dfrac{÷5}{÷5}\right)&=\dfrac{1}{2}&\text{Simplify the answer.}\end{array}[/latex]

Exercise 2

Subtract and simplify the answers.

  1.  [latex]\begin{array}{rr}&\dfrac{5}{6}\\-&\dfrac{2}{3}\\ \hline&\dfrac{1}{6}\end{array}[/latex]
  2.  [latex]\begin{array}{rr}&\dfrac{5}{6}\\-&\dfrac{2}{3}\\ \hline&\dfrac{1}{6}\end{array}[/latex]
  3. [latex]\begin{array}{rr}&\dfrac{1}{4}\\-&\dfrac{1}{12}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&\dfrac{7}{10}\\-&\dfrac{3}{5}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&\dfrac{15}{16}\\-&\dfrac{5}{8}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&\dfrac{7}{16}\\-&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&\dfrac{3}{8}\\-&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  8. [latex]\begin{array}{rr}&\dfrac{5}{6}\\-&\dfrac{1}{2}\\ \hline&\end{array}[/latex]
  9. [latex]\begin{array}{rr}&\dfrac{7}{8}\\-&\dfrac{1}{2}\\ \hline&\end{array}[/latex]
  10. [latex]\begin{array}{rr}&\dfrac{5}{8}\\-&\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  11. [latex]\begin{array}{rr}&\dfrac{2}{3}\\-&\dfrac{1}{8}\\ \hline&\end{array}[/latex]
  12. [latex]\begin{array}{rr}&\dfrac{5}{12}\\-&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  13. [latex]\begin{array}{rr}&\dfrac{1}{2}\\-&\dfrac{1}{6}\\ \hline&\end{array}[/latex]
  14. [latex]\begin{array}{rr}&\dfrac{3}{4}\\-&\dfrac{1}{10}\\ \hline&\end{array}[/latex]
  15. [latex]\begin{array}{rr}&\dfrac{1}{8}\\-&\dfrac{1}{16}\\ \hline&\end{array}[/latex]
  16. [latex]\begin{array}{rr}&\dfrac{4}{5}\\-&\dfrac{1}{2}\\ \hline&\end{array}[/latex]

Answers to Exercise 2

  1. [latex]\dfrac{1}{6}[/latex]
  2. [latex]\dfrac{1}{10}[/latex]
  3. [latex]\dfrac{5}{16}[/latex]
  4. [latex]\dfrac{3}{16}[/latex]
  5. [latex]\dfrac{1}{8}[/latex]
  6. [latex]\dfrac{3}{8}[/latex]
  7. [latex]\dfrac{7}{24}[/latex]
  8. [latex]\dfrac{13}{24}[/latex]
  9. [latex]\dfrac{1}{6}[/latex]
  10. [latex]\dfrac{1}{3}[/latex]
  11. [latex]\dfrac{13}{20}[/latex]
  12. [latex]\dfrac{1}{16}[/latex]
  13. [latex]\dfrac{3}{10}[/latex]

Subtracting mixed numbers is very similar to adding mixed numbers.

  • Find the least common denominator if the fractions do not have the same denominator already.
  • Rename the fractions as equivalent fractions using the LCD. Don’t forget to keep whole number with the problem.
  • Subtract the second denominator from the first. Keep the same denominator. Subtract the whole numbers.
  • Simplify the answer.

Example D

[latex]\begin{array}{rrr}&4\dfrac{1}{2}\left(\dfrac{\times3}{\times3}\right)&=&4\dfrac{3}{6}&\\-&3\dfrac{1}{6}&=& 3\dfrac{1}{6}\\ \hline\\&&&1\dfrac{2}{6}&=1\dfrac{1}{3} \end{array}[/latex]

Example E

[latex]\begin{array}{rrr}&12\dfrac{3}{4}\left(\dfrac{\times3}{\times3}\right)&=&12\dfrac{9}{12}\\-&\dfrac{2}{3}\left(\dfrac{\times4}{\times4}\right)&=& \dfrac{8}{12}\\ \hline\\&&&12\dfrac{1}{12}\end{array}[/latex]

Exercise 3

Work through all these questions carefully.

  1. [latex]\begin{array}{rrr}&16\dfrac{2}{3}=&16\dfrac{16}{24}\\-&4\dfrac{3}{8}=&4\dfrac{9}{24}\\ \hline\\&&12\dfrac{7}{24}\end{array}[/latex]
  2. [latex]\begin{array}{rr}&9\dfrac{7}{12}\\-&9\dfrac{5}{12}\\ \hline&\end{array}[/latex]
  3. [latex]\begin{array}{rr}&6\dfrac{3}{4}\\-&2\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&22\dfrac{5}{6}\\-&18\dfrac{2}{5}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&3\dfrac{7}{8}\\-&2\dfrac{3}{4}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&1\dfrac{7}{100}\\-&\dfrac{1}{2}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&9\dfrac{1}{4}\\-&7\\ \hline&\end{array}[/latex]
  8. [latex]\begin{array}{rr}&1\dfrac{5}{8}\\-&\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  9. [latex]\begin{array}{rr}&19\dfrac{5}{6}\\-&11\dfrac{5}{12}\\ \hline&\end{array}[/latex]

Answers to Exercise 3

  1. [latex]\dfrac{1}{6}[/latex]
  2. [latex]4\dfrac{5}{12}[/latex]
  3. [latex]4\dfrac{13}{30}[/latex]
  4. [latex]1\dfrac{1}{8}[/latex]
  5. [latex]1\dfrac{1}{5}[/latex]
  6. [latex]2\dfrac{1}{4}[/latex]
  7. [latex]1\dfrac{7}{24}[/latex]
  8. [latex]8\dfrac{5}{12}[/latex]

Subtracting Mixed Numbers from Whole Numbers

This is the start of a new process! You already have all the skills to do this, but the process is new.

Example F

Let’s look at some apples.

You have 3 whole apples and you want to give your son 1 apple and your daughter half an apple. How will you do this?

Row of 3 apples.

Yes! You will cut one apple in half.

Row of 3 apples. Last apple is cut into two pieces.

Now you have [latex]2 \tfrac{2}{2}[/latex] apples. And you can easily give away [latex]1 \tfrac{1}{2}[/latex] of them. Cross out [latex]1 \tfrac{1}{2}[/latex] apples in the drawing. How much is left?

Here is the arithmetic for what you just did.

[latex]3=2\dfrac{2}{2}-\dfrac{1}{2}=1\dfrac{1}{2}[/latex]

[latex]1\tfrac{1}{2}[/latex]apples are left

Example G

Here are 6 cans of pop to share among your friends.

6 cans of pop

4 people want a whole can, but one person is on a diet and only wants [latex]\tfrac{1}{4}[/latex] of a can. How much pop will be left?

What will you do? You will open a can and think of that can as [latex]\tfrac{4}{4}[/latex].

6 cans of pop. Last can is divided in 4.

You have [latex]5 \tfrac{4}{4}[/latex] cans of pop and you can give out 4 whole cans and [latex]\tfrac{1}{4}[/latex] can of pop. Cross out the 4 whole cans and [latex]\tfrac{1}{4}[/latex] of a can in the drawing.
How many cans are left?

Here is the arithmetic:

[latex]\begin{array}{rr} 6 =& 5 \dfrac{4}{4} \\ -& 1\dfrac{1}{4} \\ \hline & 1 \dfrac{3}{4} \end{array}[/latex]

Example H

Draw five apple pies. Plan to give away [latex]3\dfrac{2}{3}[/latex] of the pies. How many pies are left?

To do that, cut one pie into thirds. Then cross out 2 whole pies and [latex]\dfrac{2}{3}[/latex]. Here is the arithmetic.

[latex]\begin{array}{rr}5=&4\dfrac{3}{3}\\-&3\dfrac{2}{3}\\ \hline&1\dfrac{1}{3}&\text{pies left}\end{array}[/latex]

Remember [latex]1 = \dfrac{1}{1} = \dfrac{2}{2} = \dfrac{3}{3} = \dfrac{4}{4} = \dfrac{5}{5} = \dfrac{6}{6} =\dfrac{7}{7} = \dfrac{8}{8} = \dfrac{9}{9} =\dfrac{10}{10}[/latex] and so on.

To subtract a mixed number from a whole number

Step 1: “Borrow” one from the whole number.

Step 2: Rename the one as an improper fraction with the same denominator as the fraction you are taking away. (Remember to change the whole number to one less.)

Step 3: Subtract the mixed numbers.

Example I

[latex]18 - 12 \dfrac{3}{4} =[/latex]

“Borrow” 1 from 18 and change to [latex]\tfrac{4}{4}[/latex].

[latex]\begin{array}{rr} \cancel{18}17 = & 17 \dfrac{4}{4} \\ -& 12 \dfrac{3}{4} \\ \hline & 5 \dfrac{1}{4} \end{array}[/latex]

Try it yourself:

[latex]1 - \dfrac{4}{5} =[/latex]

Exercise 4

Subtract and express in lowest terms. TIP: Remember to change your whole number to a mixed numeral.

  1. [latex]\begin{array}{rr}5=&4\dfrac{2}{2}\\-&1\dfrac{1}{2}\\ \hline&2\dfrac{1}{2}\end{array}[/latex]
  2. [latex]\begin{array}{rr}&9\\-&4\dfrac{3}{10}\\ \hline&\end{array}[/latex]
  3. [latex]\begin{array}{rr}&12\\-&11\dfrac{5}{8}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&25\\-&20\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&3\\-&2\dfrac{2}{3}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&8\\-&\dfrac{3}{4}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&32\\-&28\dfrac{1}{2}\\ \hline&\end{array}[/latex]
  8. [latex]\begin{array}{rr}&5\\-&3\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  9. [latex]\begin{array}{rr}&8\\-&4\dfrac{4}{9}\\ \hline&\end{array}[/latex]

Answers to Exercise 4

  1. [latex]4\dfrac{7}{10}[/latex]
  2. [latex]\dfrac{3}{8}[/latex]
  3. [latex]4\dfrac{3}{4}[/latex]
  4. [latex]\dfrac{1}{3}[/latex]
  5. [latex]7\dfrac{1}{4}[/latex]
  6. [latex]3\dfrac{1}{2}[/latex]
  7. [latex]1\dfrac{2}{3}[/latex]
  8. [latex]3\dfrac{5}{9}[/latex]

Renaming to Subtract Mixed Numbers

Example J

Look at the [latex]3\tfrac{1}{4}[/latex] chocolate bars.

3 whole chocolate bars. One quarter of a bar.

You need to give [latex]2\tfrac{3}{4}[/latex] chocolate bars to the kids on the soccer team. How will you do this?

You will have to cut up one of the whole chocolate bars into 4 pieces, or [latex]\tfrac{4}{4}[/latex].

2 whole chocolate bars. 4 quarters of a chocolate bar. One quarter of a chocolate bar.

Now you have 2 whole bars, [latex]\tfrac{4}{4}[/latex] of a bar and [latex]\tfrac{1}{4}[/latex] of a bar which equals [latex]2\tfrac{5}{4}[/latex] of a bar. It will be easy to give away (subtract) [latex]2\tfrac{3}{4}[/latex] bars. Cross out [latex]2\tfrac{3}{4}[/latex] bars. How much is left?

Here is the arithmetic:

[latex]3\dfrac{1}{4}-2\dfrac{3}{4}=[/latex]

[latex]\begin{array}{rrr} 3 \dfrac{1}{4} = & 2 \dfrac{4}{4} + \dfrac{1}{4} = & 2 \dfrac{5}{4} \\ & - & 2 \dfrac{3}{4} \\ \hline && \dfrac{2}{4} & = \dfrac{1}{2} \text{ chocolate bar left} \end{array}[/latex]

Example K

Look at the 5 cherry pies.

Illustration of 5 cherry pies and one slice that is one eighth of a pie

You promised to send [latex]3\tfrac{5}{8}[/latex] pies to the spring party at the school. What will you do? Cut one of the pies into eighths.

Illustration of four cherry pies, plain. One cherry pie with cross hashes indicating eighths lines. And then a slice of pie that is one eighth. Illustration of problem to solve.

Do that, and the cross out [latex]3\dfrac{5}{8}[/latex] pies. How much pie is left?

[latex]\begin{array}{rr} 5\dfrac{1}{8}=4\dfrac{8}{8}+\dfrac{1}{8}=&4\dfrac{9}{8}\\ -&3\dfrac{5}{8}\\ \hline &1\dfrac{4}{8}&=1\dfrac{1}{2}\text{ pies left}\end{array}[/latex]

Renaming a mixed number so you can subtract

Step 1: Check to see if renaming is needed. That is, check that the fraction in the mixed number you are starting with is less than the fraction you want to take away.

[latex]4\dfrac{1}{3}-2\dfrac{2}{3}=[/latex]      ( [latex]\dfrac{1}{3}[/latex] is less than [latex]\dfrac{2}{3}[/latex]  )

Step 2: “Borrow” one from the whole number TIP: Remember to change the whole number to 1 less.
Step 3: Rename the “borrowed” one as an improper fraction with the same denominator as the other fractions.
[latex]4\dfrac{1}{3}=3\dfrac{3}{3}+\dfrac{1}{3}[/latex]
[latex]\tfrac{3}{3}[/latex] is the 1 that you borrowed from the four.
Step 4: Add the renamed one to the fraction that is part of the same mixed number.
[latex]3\dfrac{3}{3}+\dfrac{1}{3}=3\dfrac{4}{3}[/latex]
Step 5: Subtract as usual, expressing your answer in lowest terms.
[latex]\begin{array}{rrr}&4\dfrac{1}{3}=&3\dfrac{4}{3}\\-&2\dfrac{2}{3}=&2\dfrac{2}{3}\\ \hline&&1\dfrac{2}{3}\end{array}[/latex]

Example L

[latex]5\dfrac{2}{3}-2\dfrac{4}{5}[/latex]

Step 1: [latex]\dfrac{2}{5}[/latex] is less than [latex]\dfrac{4}{5}[/latex]

Step 2 and 3: Borrow one.

[latex]5\dfrac{2}{5}=4\dfrac{5}{5}+\dfrac{2}{5}=4\dfrac{7}{5}[/latex]

Step 4 and 5:

[latex]\begin{array}{rr}5\dfrac{2}{5}=&4\dfrac{5}{5}+\dfrac{2}{5}=&4\dfrac{7}{5} \\ -&2\dfrac{4}{5}=&2\dfrac{4}{5}\\\hline&&2\dfrac{3}{5}\end{array}[/latex]

Example M

[latex]1\dfrac{2}{4}-\dfrac{3}{4}[/latex]

Step 1: [latex]\tfrac{2}{4}[/latex] is less than [latex]\tfrac{3}{4}[/latex] so we need to rename to subtract.

Step 2, 3, 4 and 5:

[latex]\begin{array}{rrr}1\dfrac{2}{4} =&\dfrac{4}{4} +\dfrac{2}{4}=&\dfrac{6}{4} \\ -& \dfrac{3}{4} =& \dfrac{3}{4} \\ \hline &&\dfrac{3}{4} \end{array}[/latex]

Exercise 5

Subtract. Be sure the answers are in lowest terms.

  1. [latex]\begin{array}{rrr}20\dfrac{1}{4} =& 19 \dfrac{5}{4}\\-&10\dfrac{3}{4}\\ \hline&9\dfrac{2}{4}&=9\dfrac{1}{2} \end{array}[/latex]
  2. [latex]\begin{array}{rr}&3\dfrac{1}{3}\\-&1\dfrac{2}{3}\\ \hline&\end{array}[/latex]
  3. [latex]\begin{array}{rr}&56\dfrac{2}{5}\\-&20\dfrac{4}{5}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&8\dfrac{1}{3}\\-&1\dfrac{2}{3}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&4\dfrac{1}{5}\\-&2\dfrac{3}{5}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&5\dfrac{2}{7}\\-&1\dfrac{3}{7}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&12\dfrac{5}{9}\\-&10\dfrac{7}{9}\\ \hline&\end{array}[/latex]
  8.  [latex]\begin{array}{rr}&9\dfrac{3}{5}\\-&\dfrac{4}{5}\\ \hline&\end{array}[/latex]
  9. [latex]\begin{array}{rr}&15\dfrac{3}{8}\\-&14\dfrac{7}{8}\\ \hline&\end{array}[/latex]

Answers to Exercise 5

  1. [latex]1\dfrac{2}{3}[/latex]
  2. [latex]35\dfrac{3}{5}[/latex]
  3. [latex]6\dfrac{2}{3}[/latex]
  4. [latex]1\dfrac{3}{5}[/latex]
  5. [latex]3\dfrac{6}{7}[/latex]
  6. [latex]1\dfrac{7}{9}[/latex]
  7. [latex]8\dfrac{4}{5}[/latex]
  8. [latex]\dfrac{1}{2}[/latex]

Here is the last step for subtraction of fractions. Mixed numbers to be subtracted often do not have the same denominators-they are unlike fractions.

You must

  • Write equivalent fractions using the LCD.
  • Decide if you need to “borrow” or rename before you subtract.
  • Subtract and simplify the answer.

Example N

[latex]4\dfrac{1}{3}-2\dfrac{5}{6}=[/latex]

 

[latex]\begin{array}{rrr} &4\dfrac{1}{3}=4\dfrac{2}{6}=3\dfrac{6}{6} + \dfrac{2}{6}=&3\dfrac{8}{6}\\&-&2\dfrac{5}{6}\\ \hline&&1\dfrac{3}{6}&=1\dfrac{1}{2}\end{array}[/latex]

Example O

[latex]9\dfrac{1}{10} - 4\dfrac{1}{4}=[/latex]

 

[latex]\begin{array}{rrrr}9\dfrac{1}{10}=&9\dfrac{2}{20}=&8\dfrac{20}{20} + \dfrac{2}{20}= &8\dfrac{22}{20}\\ -&4\dfrac{1}{4} = &4\dfrac{5}{20} =& 4\dfrac{5}{20}\\ \hline&&&4\dfrac{17}{20}\end{array}[/latex]

Exercise 6

Subtract. Be sure the answers are in lowest terms.

  1. [latex]\begin{array}{rr}&9\dfrac{3}{8}=&9\dfrac{3}{8}=&8\dfrac{11}{8}\\-&7\dfrac{1}{2}=&7\dfrac{4}{8}=&7\dfrac{4}{8}\\ \hline&&& 1 \dfrac{7}{8} \end{array}[/latex]
  2. [latex]\begin{array}{rr}&7\dfrac{1}{16}\\-&4\dfrac{1}{8}\\ \hline&\end{array}[/latex]
  3. [latex]\begin{array}{rr}&15\dfrac{1}{6}\\-&12\dfrac{7}{8}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&20\dfrac{2}{6}\\-&16\dfrac{2}{3}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&6\dfrac{3}{5}\\-&4\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&9\dfrac{1}{4}\\-&7\dfrac{3}{8}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&5\dfrac{1}{3}\\-&2\dfrac{1}{2}\\ \hline&\end{array}[/latex]
  8. [latex]\begin{array}{rr}&18\dfrac{1}{6}\\-&12\dfrac{2}{3}\\ \hline&\end{array}[/latex]

Answers to Exercise 6

  1. [latex]2\dfrac{15}{16}[/latex]
  2. [latex]2\dfrac{7}{24}[/latex]
  3. [latex]3\dfrac{2}{3}[/latex]
  4. [latex]2\dfrac{7}{20}[/latex]
  5. [latex]1\dfrac{7}{8}[/latex]
  6. [latex]2\dfrac{5}{6}[/latex]
  7. [latex]5\dfrac{1}{2}[/latex]

Exercise 7

A Subtraction Review.

  1. [latex]\begin{array}{rr}&\dfrac{5}{8}\\-&\dfrac{1}{4}\\ \hline&\end{array}[/latex]
  2. [latex]\begin{array}{rr}&8\dfrac{3}{4}\\-&4\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  3. [latex]\begin{array}{rr}&13\dfrac{1}{3}\\-&12\dfrac{5}{6}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&7\dfrac{1}{3}\\-&4\dfrac{5}{6}\\ \hline&\end{array}[/latex]
  5. [latex]\begin{array}{rr}&9\dfrac{1}{5}\\-&6\dfrac{1}{3}\\ \hline&\end{array}[/latex]
  6. [latex]\begin{array}{rr}&7\\-&1\dfrac{7}{8}\\ \hline&\end{array}[/latex]
  7. [latex]\begin{array}{rr}&19\dfrac{2}{3}\\-&18\\ \hline&\end{array}[/latex]
  8. [latex]\begin{array}{rr}&\dfrac{5}{8}\\-&\dfrac{1}{2}\\ \hline&\end{array}[/latex]

Answers to Exercise 7

  1. [latex]\dfrac{3}{8}[/latex]
  2. [latex]4\dfrac{5}{12}[/latex]
  3. [latex]\dfrac{1}{2}[/latex]
  4. [latex]2\dfrac{1}{2}[/latex]
  5. [latex]2\dfrac{13}{15}[/latex]
  6. [latex]5\dfrac{1}{8}[/latex]
  7. [latex]1\dfrac{1}{3}[/latex]
  8. [latex]\dfrac{1}{8}[/latex]

Problems Using Subtraction of Common Fractions

Subtraction problems may ask you to:

  • find the difference between two amounts.
    • “how much more is…”
    • “how much less is…”
  • take away, give away, or lose.
  • decide how much is left or how much remains.

Read over the subtraction problems that you did in Unit Two with decimals. The wording and problem situations will be similar.

Drawing a sketch and estimating the answer using whole numbers may also be helpful.

Exercise 8

  1. The New Earth Diaper Company stocks went from [latex]5\tfrac{7}{8}[/latex] to [latex]7\tfrac{3}{8}[/latex]this week. How much did the stocks increase in value?
  2. Jean is knitting an afghan which will be made from 5 long pieces. She has finished [latex]3\tfrac{2}{3}[/latex] of the pieces. How many pieces does she still have to knit?
  3. Dave said he worked in the garden for [latex]6\tfrac{1}{4}[/latex] hours, but his wife saw him snoozing under a tree for [latex]1\tfrac{1}{2}[/latex] hours! How long did Dave really work?
  4. Maureen left [latex]\tfrac{2}{3}[/latex] of a big lasagne casserole in the fridge hoping it would be enough for a quick dinner that night. But alas, when she got home, only [latex]\tfrac{1}{4}[/latex] of the big lasagne casserole remained. How much of the lasagne was eaten while she was out?
  5. In the first half of 1992, the Bank of Canada Prime Rate dropped steadily. It started the year at [latex]8\tfrac{1}{2}[/latex] % and was at a low [latex]6\tfrac{3}{4}[/latex]% in July. How many percentage points did the prime rate drop? (Note: treat the % just like a unit in this problem.)
  6. Mark is [latex]1\tfrac{3}{4}[/latex] metres tall. His partner is [latex]1\tfrac{1}{3}[/latex] metres tall. How much taller is Mark than his partner?
  7. A teenager can drink [latex]3\tfrac{3}{4}[/latex] litres of water each day. If this teenager drinks [latex]2\tfrac{1}{2}[/latex] litres of water by lunch, how much more water will he drink in the day?
  8. Joan bought [latex]13\tfrac{1}{2}[/latex] metres to do her sewing project. She has used [latex]8\tfrac{1}{5}[/latex] metres so far. How much material does she have left?

Answers to Exercise 8

  1. [latex]1\dfrac{1}{2}[/latex] or $1.50
  2. [latex]1\dfrac{1}{3}[/latex] pieces
  3. [latex]4\dfrac{3}{4}[/latex] hours
  4. [latex]\dfrac{5}{12}[/latex] of the lasagna
  5. [latex]1\dfrac{3}{4}[/latex] percentage points
  6. [latex]\dfrac{5}{12}[/latex] metres taller
  7. [latex]1\dfrac{1}{4}[/latex] litres left to drink
  8. [latex]5\dfrac{3}{10}[/latex] metres left

Topic B Self-Test

Mark         /15   Aim 12/15

A. Subtract these fractions. Simplify the answers when necessary (15 marks).

  1. [latex]\begin{array}{rr}&\dfrac{7}{8}\\-&\dfrac{1}{8}\\ \hline&\end{array}[/latex]
  2. [latex]\begin{array}{rr}&\dfrac{11}{15}\\-&\dfrac{4}{15}\\ \hline&\end{array}[/latex]
  3. [latex]\begin{array}{rr}&\dfrac{7}{8}\\-&\dfrac{3}{16}\\ \hline&\end{array}[/latex]
  4. [latex]\begin{array}{rr}&\dfrac{2}{3}\\-&\dfrac{1}{6}\\ \hline\end{array}[/latex]
  5. [latex]\begin{array}{rr}&\dfrac{4}{7}\\-&\dfrac{1}{14}\\ \hline\end{array}[/latex]
  6. [latex]\begin{array}{rr}&\dfrac{4}{5}\\-&\dfrac{3}{8}\\ \hline\end{array}[/latex]
  7. [latex]\begin{array}{rr}&4\\-&2\dfrac{1}{2}\\ \hline\end{array}[/latex]
  8. [latex]\begin{array}{rr}&5\\-&4\dfrac{7}{8}\\ \hline\end{array}[/latex]
  9. [latex]\begin{array}{rr}&10\dfrac{3}{5}\\-&3\dfrac{3}{10}\\ \hline\end{array}[/latex]
  10. [latex]\begin{array}{rr}&7\dfrac{1}{5}\\-&3\dfrac{4}{5}\\ \hline\end{array}[/latex]
  11. [latex]\begin{array}{rr}&12\dfrac{1}{8}\\-&11\\ \hline\end{array}[/latex]
  12. [latex]\begin{array}{rr}&9\dfrac{1}{5}\\-&\dfrac{1}{4}\\ \hline\end{array}[/latex]
  13. [latex]\begin{array}{rr}&5\dfrac{1}{4}\\-&1\dfrac{2}{3}\\ \hline\end{array}[/latex]
  14. [latex]\begin{array}{rr}&10\dfrac{1}{2}\\-&2\dfrac{2}{5}\\ \hline\end{array}[/latex]
  15. [latex]\begin{array}{rr}&6\dfrac{2}{3}\\-&4\dfrac{3}{8}\\ \hline\end{array}[/latex]

Answers to Topic B Self-Test

  1. [latex]\dfrac{3}{4}[/latex]
  2. [latex]\dfrac{7}{15}[/latex]
  3. [latex]\dfrac{11}{16}[/latex]
  4. [latex]\dfrac{1}{2}[/latex]
  5. [latex]\dfrac{1}{2}[/latex]
  6. [latex]\dfrac{17}{40}[/latex]
  7. [latex]1\dfrac{1}{2}[/latex]
  8. [latex]\dfrac{1}{8}[/latex]
  9. [latex]7\dfrac{3}{10}[/latex]
  10. [latex]3\dfrac{2}{5}[/latex]
  11. [latex]1\dfrac{1}{8}[/latex]
  12. [latex]8\dfrac{19}{20}[/latex]
  13. [latex]3\dfrac{7}{12}[/latex]
  14. [latex]8\dfrac{1}{10}[/latex]
  15. [latex]2\dfrac{7}{24}[/latex]
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Adult Literacy Fundamental Mathematics: Book 5 - 2nd Edition Copyright © 2023 by Liz Girard; Wendy Tagami; and Leanne Caillier-Smith is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book