Unit 1: Common Fractions
Topic B: Common Fractions
There are three types of fractions:
- Proper fractions are part of the whole thing.
- Improper fractions are equal to 1 or are greater than 1.
- Mixed numbers are greater than one.
In a proper fraction, the numerator is smaller than the denominator. Proper fractions are less than one.
- [latex]\dfrac{3}{4}<1[/latex]
- [latex]\dfrac{2}{5}<1[/latex]
- [latex]\dfrac{9}{10}<1[/latex]
- [latex]\dfrac{4}{7}<1[/latex]
In improper fractions, the numerator is the same or larger than the denominator.
- [latex]\dfrac{4}{4}=1[/latex]
- [latex]\dfrac{3}{3}=1[/latex]
- [latex]\dfrac{8}{3}>1[/latex]
- [latex]\dfrac{9}{7}>1[/latex]
In mixed numbers, a whole number and a proper fraction are used together.
- [latex]1\dfrac{1}{2}>1[/latex]
- [latex]4\dfrac{3}{7}>1[/latex]
- [latex]3\dfrac{2}{5}>1[/latex]
- [latex]1\dfrac{9}{10}>1[/latex]
Here are some pictures to visualize mixed numbers:
Example A

You want to give three small children only [latex]\tfrac{1}{2}[/latex] an apple each. You need three half apples. You can write that as [latex]\tfrac{3}{2}[/latex] (three-halves). How will you get [latex]\tfrac{3}{2}[/latex] of an apple?
You must use more than one apple.
[latex]\tfrac{3}{2} = 1\tfrac{1}{2}[/latex] apples
This is one whole apple and [latex]\tfrac{1}{2}[/latex] of another one.
Example B

10 pieces of pizza are shown. Each pizza was cut into 8 pieces, so the fraction can be written as [latex]\tfrac{10}{8}[/latex]. This is an improper fraction; it can also be written as a mixed number: [latex]1\tfrac{2}{8}[/latex]. This is 1 whole pizza, and [latex]\tfrac{2}{8}[/latex] of another one.
Exercise 1
Answer these questions.

- How many pieces of apple are shown?
- Each apple was cut into 4 pieces, so the denominator is .
- Write the improper fraction that describes the photo.
- The photo shows whole apple and of a second apple.
- Write the mixed number that describes the apple.

- How many pieces of pizza are shown?
- Each pizza was cut into 8 pieces, so the denominator is .
- Write the improper fraction that describes the photo.
- The photo shows whole pizzas and of a third pizza.
- Write the mixed number that describes the pizza.
Answers to Exercise 1
- Apples.
- [latex]7[/latex]
- [latex]4[/latex]
- [latex]\dfrac{7}{4}[/latex]
- [latex]1\text{ and }\dfrac{3}{4}[/latex]
- [latex]1\dfrac{3}{4}[/latex]
- Pizza.
- [latex]21[/latex]
- [latex]8[/latex]
- [latex]\dfrac{21}{8}[/latex]
- [latex]2\text{ and }\dfrac{5}{8}[/latex]
- [latex]2\dfrac{5}{8}[/latex]
Exercise 2
Write the improper fraction and the mixed number that describe the shaded part in each drawing. First decide on the denominator. The denominator is what one whole thing has been divided into.
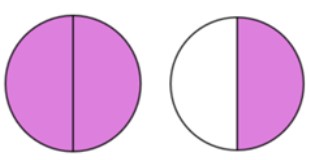
Answer: [latex]\dfrac{3}{2}=1\dfrac{1}{2}[/latex]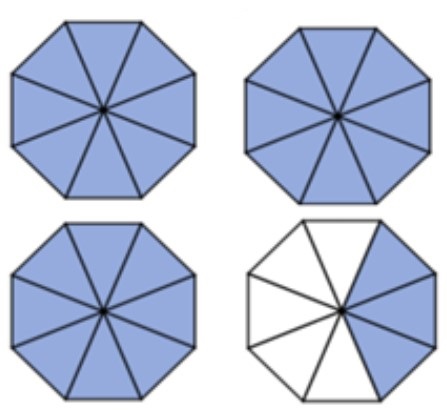

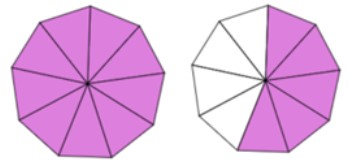

Answers to Exercise 2
- [latex]\dfrac{27}{8} = 3\dfrac{3}{8}[/latex]
- [latex]\dfrac{32}{6} = 5\dfrac{2}{6}[/latex]
- [latex]\dfrac{14}{9} = 1\dfrac{5}{9}[/latex]
- [latex]\dfrac{11}{4} = 2\dfrac{3}{4}[/latex]
Now it is your turn to draw some mixed numbers. The following is an example of how to do that.
Example C
Shade in this fraction: [latex]4\dfrac{3}{4}[/latex]
(Note: you will not need to use all the squares drawn below.)

Exercise 3
Shade the following mixed fractions in the given shapes.
- [latex]2\dfrac{3}{5}\hspace{1cm}[/latex]

- [latex]3\dfrac{2}{3}\hspace{1cm}[/latex]

- [latex]5\dfrac{1}{4}\hspace{1cm}[/latex]

- [latex]1\dfrac{1}{2}\hspace{1cm}[/latex]

Draw the following mixed fractions:
- [latex]4\dfrac{1}{2}[/latex]
- [latex]3\dfrac{4}{5}[/latex]
- [latex]2\dfrac{2}{3}[/latex]
- [latex]5\dfrac{3}{4}[/latex]
Answers to Exercise 3
Writing Improper Fractions as Mixed Numbers
In the last exercise you were able to write (rename) an improper fraction as a mixed number by looking at the drawing – you could see how many whole things were represented. You could see that if the denominator was 3, every time you had [latex]\tfrac{3}{3}[/latex] ![]() that was one whole. If the denominator was 6, every time you had [latex]\tfrac{6}{6}[/latex]
that was one whole. If the denominator was 6, every time you had [latex]\tfrac{6}{6}[/latex] ![]() that was one whole, and so on. An improper fraction is written (renamed) as a mixed number by dividing the numerator by the number of parts in the whole (the denominator).
that was one whole, and so on. An improper fraction is written (renamed) as a mixed number by dividing the numerator by the number of parts in the whole (the denominator).
Example D
Write [latex]\tfrac{8}{5}[/latex] as a mixed number.
First, write as a long division problem or as a short division question.
[latex]\require{enclose}\text{denominator}\enclose{longdiv}{\text{numerator}}=5\enclose{longdiv}{8}[/latex]
[latex]\text{numerator}\div\text{denominator} = 8\div5[/latex]
Second, divide. Write the remainder as a fraction, using the same denominator.
- The 1 becomes the whole number.
- Use the remainder (3) as the numerator
- Use the divisor (5) as the denominator.
[latex]\begin{array}{r}1\\ 5\enclose{longdiv}{8}\\-5\\ \hline\text{R }3\end{array}[/latex] or [latex]8\div5=1\text{ R }3[/latex]
[latex]\dfrac{8}{5}=1\dfrac{3}{5}[/latex]
Example E
Write [latex]\tfrac{16}{4}[/latex] as a mixed number.
[latex]4\enclose{longdiv}{16}[/latex] or [latex]16\div4[/latex]
[latex]\begin{array}{r}4\\ 4\enclose{longdiv}{16}\\-16\\ \hline0\end{array}[/latex] or [latex]16\div4=4[/latex]
[latex]\dfrac{16}{4}=4[/latex]
Exercise 4
Rewrite each improper fraction as an equivalent mixed number or whole number.
- [latex]\dfrac{9}{2}=[/latex]
- [latex]\dfrac{11}{10}=[/latex]
- [latex]\dfrac{20}{4}=[/latex]
- [latex]\dfrac{17}{6}=[/latex]
- [latex]\dfrac{13}{3}=[/latex]
- [latex]\dfrac{20}{10}=[/latex]
- [latex]\dfrac{7}{4}=[/latex]
Answers to Exercise 4
- [latex]4\dfrac{1}{2}[/latex]
- [latex]1\dfrac{1}{10}[/latex]
- [latex]5[/latex]
- [latex]2\dfrac{5}{6}[/latex]
- [latex]4\dfrac{1}{3}[/latex]
- [latex]2[/latex]
- [latex]1\dfrac{3}{4}[/latex]
Renaming Mixed Numbers as Improper Fractions
This process will be used when you multiply and divide common fractions and when you “borrow” in subtraction.
Example F
Take the whole number 2.
Here are 2 equal shapes.

The shapes are each divided into 3 parts (thirds).

How many thirds are there? 6 thirds.
[latex]2 =\dfrac{6}{3}[/latex]
Example G
Take the whole number 1.
Draw one shape (a circle or a box).

Now divide the shape into half.

How many halves are there? [latex]1=\dfrac{2}{2}[/latex]
Have you found the shortcut?
The shortcut to rename a whole number as an improper fraction is to multiply the whole number by the denominator.
- [latex]2 = \dfrac{}{4}\hspace{1cm}[/latex]Each whole number has 4 equal parts (4 quarters) in it,
- so [latex]2\text{ (whole numbers)}\times4\text{ (parts)} = 8\text{ parts}[/latex]
- so [latex]2 = \dfrac{8}{4}[/latex]
- [latex]6 = \dfrac{}{2}\hspace{1cm}[/latex]Each whole number has 2 equal parts (2 halves),
- so [latex]6\text{ (whole numbers)}\times2\text{ (parts)}=12\text{ parts}[/latex]
- so [latex]6= \dfrac{12}{2}[/latex]
- [latex]8 = \dfrac{}{3}[/latex]
- [latex]8\times3=24[/latex]
- so [latex]8 = \dfrac{24}{3}[/latex]
Exercise 5
Rename each whole number as an improper fraction using the denominator shown.
- [latex]6 = \dfrac{24}{4}[/latex], [latex]2 = \dfrac{}{3}[/latex], [latex]4 = \dfrac{}{3}[/latex], [latex]8 = \dfrac{}{10}[/latex]
- [latex]7 = \dfrac{}{3}[/latex], [latex]1 = \dfrac{}{4}[/latex], [latex]6 = \dfrac{}{10}[/latex], [latex]5 = \dfrac{}{6}[/latex]
Answers to Exercise 5
- [latex]\dfrac{24}{4}[/latex],[latex]\dfrac{6}{3}[/latex],[latex]\dfrac{12}{3}[/latex],[latex]\dfrac{80}{10}[/latex]
- [latex]\dfrac{21}{3}[/latex],[latex]\dfrac{4}{4}[/latex],[latex]\dfrac{60}{10}[/latex],[latex]\dfrac{30}{6}[/latex]
Now let’s take this idea further. How can you rename a mixed number as an improper fraction?
Example H
Take the mixed number [latex]2\tfrac{1}{4}[/latex]. This is two whole things and part of a third whole thing.
Here are three equal shapes divided into fourths.

Shade in two whole shapes [latex]\tfrac{9}{4}[/latex] and [latex]\tfrac{1}{4}[/latex] of the third shape.
How many fourths have you shaded in all? 9 fourths
[latex]2\dfrac{1}{4} = \dfrac{9}{4}[/latex]
Example I
Take the mixed number [latex]1\tfrac{2}{3}[/latex]. This is one whole thing and part of a second whole thing.
Draw two equal shapes and divide them into thirds.
Shade in one whole shape [latex]\tfrac{3}{3}[/latex] and [latex]\tfrac{2}{3}[/latex] of the second shape.

How many thirds have you shaded in all? thirds
[latex]1\dfrac{2}{3}=\dfrac{}{3}[/latex]
To rename a mixed number as an improper fraction, multiply the whole number by the denominator of the fraction and then add this to the numerator. Write the total as the new numerator over the denominator.
[latex]3\dfrac{1}{4}=\dfrac{}{4}[/latex][latex]\hspace{1cm}[/latex] [latex]3=\dfrac{12}{4}[/latex], so [latex]=3\dfrac{1}{4}=\dfrac{12}{4}+\dfrac{1}{4}=\dfrac{13}{4}[/latex]
[latex]2\dfrac{1}{2}\hspace{1cm}[/latex] [latex]2\times2=\dfrac{4}{2}+\dfrac{1}{2}=\dfrac{5}{2}[/latex]
Exercise 6
Rename each mixed number as an improper fraction.
- [latex]2\dfrac{4}{5} = \dfrac{14}{5}[/latex]
- [latex]8\dfrac{3}{8} = \dfrac{67}{8}[/latex]
- [latex]6\dfrac{5}{8} = \dfrac{}{8}[/latex]
- [latex]5\dfrac{1}{2} = \dfrac{}{2}[/latex]
- [latex]8\dfrac{4}{5} =[/latex]
- [latex]6\dfrac{1}{8} =[/latex]
- [latex]5\dfrac{3}{6} =[/latex]
- [latex]2\dfrac{7}{8} =[/latex]
- [latex]1\dfrac{8}{10} =[/latex]
- [latex]3\dfrac{6}{8} =[/latex]
Answers to Exercise 6
- [latex]\dfrac{14}{5}[/latex]
- [latex]\dfrac{67}{8}[/latex]
- [latex]\dfrac{53}{8}[/latex]
- [latex]\dfrac{11}{2}[/latex]
- [latex]\dfrac{44}{5}[/latex]
- [latex]\dfrac{49}{8}[/latex]
- [latex]\dfrac{33}{6}[/latex]
- [latex]\dfrac{23}{8}[/latex]
- [latex]\dfrac{18}{10}[/latex]
- [latex]\dfrac{30}{8}[/latex]
To Say or Write a Mixed Number
If you want to say these strange looking fractions out loud, do as follows.
Write or say: the whole number + and + the fraction
- [latex]3\tfrac{2}{5} =[/latex] three and two fifths
- [latex]5\tfrac{1}{6} =[/latex] five and one sixth
Exercise 7
Write the following fractions as words.
- [latex]2\dfrac{1}{8}[/latex]
- [latex]4\dfrac{3}{4}[/latex]
- [latex]1\dfrac{1}{2}[/latex]
- [latex]3\dfrac{3}{4}[/latex]
Answers to Exercise 7
- Two and one eighth
- Four and three fourths (or four and three quarters)
- One and one half
- Three and three fourths (or three and three quarters)
Topic B: Self-Test
Mark /12 Aim 9/12
- Write the improper fraction and the mixed number that describe the shaded part of the drawings in each question (4 marks).
- Rename each improper fraction as an equivalent mixed number or whole number (4 marks).
- [latex]\dfrac{9}{4}=[/latex]
- [latex]\dfrac{12}{3}=[/latex]
- [latex]\dfrac{5}{3}=[/latex]
- [latex]\dfrac{7}{2}=[/latex]
- Rename as improper fractions (4 marks).
- [latex]3\dfrac{1}{2}=[/latex]
- [latex]4\dfrac{3}{8}=[/latex]
- [latex]1\dfrac{7}{8}=[/latex]
- [latex]2\dfrac{5}{6}=[/latex]
Answers to Topic B Self-Test
- Write the improper fraction and the mixed number that describe the shaded part of the drawings in each question.
- [latex]\dfrac{10}{3} = 3\dfrac{1}{3}[/latex]
- [latex]\dfrac{7}{4} = 1\dfrac{3}{4}[/latex]
- Rename each improper fraction as an equivalent mixed number or whole number.
- [latex]2\dfrac{1}{4}[/latex]
- [latex]4[/latex]
- [latex]1\dfrac{2}{3}[/latex]
- [latex]3\dfrac{1}{2}[/latex]
- Rename as improper fractions.
- [latex]\dfrac{7}{2}[/latex]
- [latex]\dfrac{35}{8}[/latex]
- [latex]\dfrac{15}{8}[/latex]
- [latex]\dfrac{17}{6}[/latex]
A common fraction with a value less than one.
A common fraction with a value equal to or more than one.
A whole number and a common fraction. 1 3/4
The amount left when a divisor does not divide evenly into the dividend. The remainder must be less than the divisor.
The amount altogether.