Unit 2: Equivalent Fractions
Topic A: Equivalent Fractions
Start from the left side of each drawing and shade in the fraction shown. Below is the whole shape.

Shade [latex]\tfrac{1}{2}[/latex]

Shade [latex]\tfrac{2}{4}[/latex]

Shade [latex]\tfrac{3}{6}[/latex]

Shade [latex]\tfrac{4}{8}[/latex]

Shade [latex]\tfrac{5}{10}[/latex]

Did you notice that the amount you shaded was the same in each drawing?
The fractions that you were asked to shade are equivalent fractions. Equivalent fractions are fractions that are equal.
Now shade the fractions asked for in these drawings, the same way.
Below is the whole shape.

Shade [latex]\tfrac{1}{3}[/latex]

Shade [latex]\tfrac{2}{6}[/latex]

Shade [latex]\tfrac{3}{9}[/latex]

Shade [latex]\tfrac{4}{12}[/latex]

Shade [latex]\tfrac{5}{15}[/latex]

These above examples are all equivalent fractions.
[latex]\dfrac{1}{3}[/latex] = [latex]\dfrac{2}{6}[/latex] = [latex]\dfrac{3}{9}[/latex] = [latex]\dfrac{4}{12}[/latex] = [latex]\dfrac{5}{15}[/latex]
![]() To work with common fractions, it is often necessary to use an equivalent fraction in place of the fraction that is given. There are several processes to learn which will help you to find equivalent fractions.
To work with common fractions, it is often necessary to use an equivalent fraction in place of the fraction that is given. There are several processes to learn which will help you to find equivalent fractions.
Factors
Factors are the numbers which are multiplied together to make a product. An understanding of factors is needed to express fractions in lowest terms.
Example A
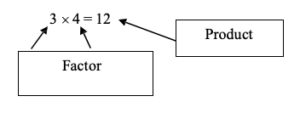
We say, “The factors of 12 are 3 and 4.”
Does 12 have any other factors?
What other numbers can be multiplied together to equal 12?
- [latex]1 \times 12 = 12[/latex] or [latex]12 \times 1 = 12[/latex]
- [latex]2 \times 6 = 12[/latex] or [latex]6 \times 2 = 12[/latex]
- [latex]3 \times 4 = 12[/latex] or [latex]4 \times 3 = 12[/latex]
The factors of 12 are 1, 2, 3, 4, 6, 12.
Example B
Find the factors of 10.
- [latex]1 \times 10 = 10[/latex]
- [latex]2 \times 5 = 10[/latex]
The factors of 10 are 1, 2, 5, 10.
Example C
Find the factors of 9.
- [latex]1 \times 9 = 9[/latex]
- [latex]3 \times 3 = 9[/latex]
The factors of 9 are 1, 3, 9.
Exercise 1
Find all the factors
- The factors of 16: [latex]1 \times 16 = 16; 2 \times 8 = 16; 4 \times 4 = 16[/latex] The factors of 16 are 1, 2, 4, 8, 16.
- The factors of 4: [latex]1 \times 4 = 4; 2 \times 2 = 4[/latex] The factors of 4 are 1, 2, 4.
- The factors of 8:
- The factors of 20:
- The factors of 5:
- The factors of 15:
- The factors of 21:
- The factors of 6:
- The factors of 25:
Answers to Exercise 1
- 1, 2, 4, 8
- 1, 2, 4, 5, 10, 20
- 1, 5
- 1, 3, 5, 15
- 1, 3, 7, 21
- 1, 2, 3, 6
- 1, 5, 25
Some numbers only have two factors, 1 and the number itself. These numbers are called prime numbers. Look at the chart for some prime numbers.
| Prime Numbers | Factors |
|---|---|
| 1 | 1, 1 |
| 2 | 1, 2 |
| 3 | 1, 3 |
| 5 | 1, 5 |
| 7 | 1, 7 |
| 11 | 1, 11 |
| 13 | 1, 13 |
| 17 | 1, 17 |
| 19 | 1, 19 |
| 23 | 1, 23 |
| 29 | 1, 29 |
Add other prime numbers to the chart as you find them.
Reminder: Prime numbers only have two, prime factors.
Finding Common Factors
A common factor is a number used to reduce the numerator and denominator.
Example D
What are the common factors for the numerator and denominator of [latex]\tfrac{4}{6}[/latex]?
- Find the factors of 4 and 6.
- The factors of 4 are 1, 2, 4.
- The factors of 6 are 1, 2, 3, 6.
What factors do 4 and 6 have in common?
- 4: 1, 2, 4
- 6: 1, 2, 3, 6
The common factors of 4 and 6 are 1 and 2
For the above equation, the factors are 1 and 2; however, 1 is not used as a common factor. This is because 1 is a factor of all whole numbers.
Example E
What are the common factors for the numerator and denominator of [latex]\tfrac{6}{15}[/latex]?
- Find the factors of 6 and 15.
- The factors of 6 are 1, 2, 3,6
- The factors of 15 are 1, 3,5,15.
What factors do 6 and 15 have in common?
- 6: 1, 2, 3,6
- 15: 1, 3,5,15
The common factor of 6 and 15 is 3.
Example F
What are the common factors for the numerator and denominator of [latex]\tfrac{16}{24}[/latex]?
- Find the factors of 16 are 1, 2, 4, 8, 16
- The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
- The common factors of 16 and 24 are: 2, 4, 8
- 8 is called the greatest common factor (GCF) of 16 and 24 because it is the largest of all the common factors.
Exercise 2
Find the Common Factors for each set of numbers. Then identify the Greatest Common Factor (GCF).
- 10, 15
- Factors of 10: 1, 2, 5, 10
- Factors of 15: 1, 3, 5, 15
- Common factors: 5
- Greatest common factor: 5
- 4, 16
- Factors of 4: 1, 2, 4
- Factors of 16: 1, 2, 4, 8, 16
- Common factors: 2, 4
- Greatest common factor: 4
- 9,12
- Factors of 9:
- Factors of 12:
- Common factors:
- Greatest common factor:
- 20, 30
- Factors of 20:
- Factors of 30:
- Common factors:
- Greatest common factor:
- 18, 12
- Factors of 18:
- Factors of 12:
- Common factors:
- Greatest common factor:
- 24, 32
- Factors of 24:
- Factors of 32:
- Common factors:
- Greatest common factor:
- 8, 12
- Factors of 8:
- Factors of 12:
- Common factors:
- Greatest common factor:
- 6, 9
- Factors of 6:
- Factors of 9:
- Common factors:
- Greatest common factor:
- 9,15
- Factors of 9:
- Factors of 15:
- Common factors:
- Greatest common factor:
Answers to Exercise 2
- 10, 15
- Factors of 10: 1, 2, 5, 10
- Factors of 15: 1, 3, 5, 15
- Common factors: 5
- Greatest common factor: 5
- 4, 16
- Factors of 4: 1, 2, 4
- Factors of 16: 1, 2, 4, 8, 16
- Common factors: 2, 4
- Greatest common factor: 4
- 9,12
- Factors of 9: 1, 3, 9
- Factors of 12: 1, 2, 3, 4, 6, 12
- Common factors: 3
- Greatest common factor: 3
- 20, 30
- Factors of 20: 1, 2, 4, 5, 10, 20
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Common factors: 2, 5, 10
- Greatest common factor: 10
- 18, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 12:, 1, 2, 3, 4, 6, 12
- Common factors: 2, 3, 6
- Greatest common factor: 6
- 24, 32
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 32:, 1, 2, 4, 8, 16, 32
- Common factors: 2, 4, 8
- Greatest common factor: 8
- 8, 12
- Factors of 8: 1, 2, 4, 8
- Factors of 12: 1, 2, 3, 4, 6, 12
- Common factors: 2, 4
- Greatest common factor: 4
- 6, 9
- Factors of 6: 1, 2, 3, 6
- Factors of 9: 1, 3, 9
- Common factors: 3
- Greatest common factor: 3
- 9, 15
- Factors of 9: 1, 3, 9
- Factors of 15: 1, 3, 5, 15
- Common factors: 3
- Greatest common factor: 3
Expressing Fractions in Lower Terms
Express means to say it or write it.
Lower terms means to express equivalent fractions with smaller (lower) denominators.
Look back to the first example with the rectangles at the beginning of this topic. The equivalent fraction in lowest terms is [latex]\tfrac{1}{2}[/latex] .
The words simplify and reduce are another way to say “express fractions in lower (or lowest) terms.”
To express a fraction in lowest terms, do this:
Step 1: Find the greatest common factor (GCF) of the numerator and denominator.
- [latex]\dfrac{4}{12}[/latex] The factors of 4 are 1, 2, 4
- The factors of 12 are 1, 2, 3, 4, 6, 12
The GCF is 4.
Step 2: Divide the numerator and the denominator by the greatest common factor.
- [latex]\dfrac{4\div 4}{12\div 4}=\dfrac{1}{3}[/latex]
- [latex]\dfrac{4}{12}[/latex] = [latex]\dfrac{1}{3}[/latex]
Example G
How would you reduce [latex]\dfrac{6}{9}[/latex]?
The factors of 6 are 1, 2, 3, 6.
The factors of 9 are 1, 3, 9.
The GCF is 3.
- [latex]\dfrac{6\div 3}{9\div 3}= \dfrac{2}{3}[/latex]
- [latex]\dfrac{6}{9} = \dfrac{2}{3}[/latex]
Example H
How would you reduce [latex]\dfrac{15}{24}[/latex]?
The factors of 15 are 1, 3, 5, 15.
The factors of 24 are 1, 3, 4, 6, 8, 24.
The GCF is 3.
- [latex]\dfrac{15\div 3}{24\div 3} =\dfrac{5}{8}[/latex]
- [latex]\dfrac{15}{24} = \dfrac{5}{8}[/latex]
There are several reasons lower terms are used:
- The math is usually easier with lower numbers.
- Is it easier to think of [latex]\tfrac{1}{2}[/latex] an apple or [latex]\tfrac{15}{30}[/latex] of an apple? [latex]\left( \tfrac{1}{2}=\tfrac{15}{30}\right)[/latex]
- Do you want to think about [latex]\tfrac{155}{620}[/latex] of your pay cheque or [latex]\tfrac{1}{4}[/latex] of your pay cheque? [latex]\left(\tfrac{1}{4}=\tfrac{155}{620}\right)[/latex]
- Always express fractions in lowest terms!
Dividing both the numerator and denominator by the GCF will give an equivalent fraction in lower terms.
Exercise 3
Express each fraction in lowest terms. (The directions could also say, “Simplify each fraction,” or “Reduce these fractions.”)
- [latex]\dfrac{2\div 2}{4\div 2}= \dfrac{1}{2}[/latex], [latex]\dfrac{3\div \ \ \ }{9\div \ \ \ }[/latex] =
- [latex]\dfrac{2\div 2}{12\div 2}=\dfrac{1}{6}[/latex], [latex]\dfrac{3 \div \ \ \ }{15 \div \ \ \ }[/latex] =
- [latex]\dfrac{5\div \ \ \ }{10\div \ \ \ }[/latex] = , [latex]\dfrac{4\div \ \ \ }{24\div \ \ \ }[/latex] =
- [latex]\dfrac{10\div \ \ \ }{25\div \ \ \ }[/latex] = [latex]\dfrac{9\div \ \ \ }{12\div \ \ \ }[/latex] =
Make sure that you write in the GCF you are dividing with. Do not skip this step until you are absolutely sure you can do it correctly in your head each time.
(Good mathematicians know when to skip steps and when not to… sometimes easy steps are never skipped by good mathematicians).
- [latex]\dfrac{3}{30}[/latex] = [latex]\dfrac{6}{10}[/latex] =
- [latex]\dfrac{9}{24}[/latex] = [latex]\dfrac{18}{27}[/latex] =
- [latex]\dfrac{4}{16}[/latex] = [latex]\dfrac{3}{12}[/latex] =
- [latex]\dfrac{15}{24}[/latex] = [latex]\dfrac{15}{25}[/latex] =
- [latex]\dfrac{2}{32}[/latex] = [latex]\dfrac{6}{20}[/latex] =
- [latex]\dfrac{1}{2}[/latex], [latex]\dfrac{1}{3}[/latex]
- [latex]\dfrac{1}{6}[/latex], [latex]\dfrac{1}{5}[/latex]
- [latex]\dfrac{1}{2}[/latex], [latex]\dfrac{1}{6}[/latex]
- [latex]\dfrac{2}{5}[/latex], [latex]\dfrac{3}{4}[/latex]
- [latex]\dfrac{1}{10}[/latex], [latex]\dfrac{3}{5}[/latex]
- [latex]\dfrac{3}{8}[/latex], [latex]\dfrac{2}{3}[/latex]
- [latex]\dfrac{1}{4}[/latex], [latex]\dfrac{1}{4}[/latex]
- [latex]\dfrac{5}{8}[/latex], [latex]\dfrac{3}{5}[/latex]
- [latex]\dfrac{1}{16}[/latex], [latex]\dfrac{3}{10}[/latex]
Expressing Fractions in Higher Terms
Higher Terms are needed when you add and subtract fractions with different denominators.
You have learned that dividing both the numerator and denominator of a fraction by a common factor gives an equivalent fraction in lower terms. You know that dividing and multiplying are opposite operations, so this next rule will match the one you just learned for reducing:
Multiplying both the numerator and denominator of a fraction by the same number (a common factor) will give an equivalent fraction in higher terms.
Example I
[latex]\dfrac{3}{5}\left(\dfrac{\times 2}{\times 2}\right)=\dfrac{6}{10}[/latex]
[latex]\dfrac{3}{5}=\dfrac{6}{10}[/latex]
Example J
[latex]\dfrac{1}{2}\left(\dfrac{\times 8}{\times 8}\right)=\dfrac{8}{16}[/latex]
[latex]\dfrac{1}{2}= \dfrac{8}{16}[/latex]
Example K
[latex]\dfrac{2}{3}\left(\dfrac{\times 3}{\times 3}\right)=\dfrac{6}{9}[/latex]
[latex]\dfrac{2}{3} = \dfrac{6}{9}[/latex]
Are the Fractions Equivalent?
If the denominators are the same, you can easily judge if the fractions are equivalent by comparing the numerators.
Compare [latex]\tfrac{4}{5}[/latex] and [latex]\tfrac{3}{5}[/latex]: [latex]\tfrac{4}{5}[/latex] ≠ [latex]\tfrac{3}{5}[/latex] (≠ means ‘not equal’)
Compare [latex]\tfrac{12}{20}[/latex] and [latex]\tfrac{12}{20}[/latex]: [latex]\tfrac{12}{20} = \tfrac{12}{20}[/latex]
If the denominators are different, you might be able to rewrite one or more of the fractions so they have the same denominator.
Compare [latex]\tfrac{4}{5}[/latex] and [latex]\tfrac{6}{10}[/latex]: [latex]\tfrac{6}{10}\tfrac{\div 2}{\div 2}[/latex]=[latex]\tfrac{3}{5}[/latex] So:[latex]\tfrac{4}{5}\neq \tfrac{3}{5}[/latex]
Compare [latex]\tfrac{12}{16}[/latex] and [latex]\tfrac{5}{8}[/latex]: [latex]\tfrac{5}{8} \tfrac{\times 2}{\times 2}[/latex] =[latex]\tfrac{10}{16}[/latex] So:[latex]\tfrac{12}{16}\neq \tfrac{10}{16}[/latex]
or you could do this: [latex]\tfrac{12}{16}[/latex][latex]\tfrac{\div 2}{\div 2}= \tfrac{6}{8}[/latex] So:[latex]\tfrac{6}{8}\neq\tfrac{5}{8}[/latex]
A quick method is to cross multiply:
- multiply the numerator of one fraction by the denominator of the second fraction
- multiply the numerator of the other fraction by the denominator of the first fraction These are called the cross-products.
If the cross products are the same, then the fraction is equivalent.
Look at the examples:
Example L
Compare [latex]\dfrac{4}{7}[/latex] and [latex]\dfrac{5}{9}[/latex]
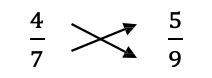
- Multiply the numerator 4 by the denominator 9
- [latex]4 \times 9 = 36[/latex]
- Multiply the denominator 7 by the numerator 5
- [latex]7 \times 5 = 35[/latex]
- The products 36 and 35 are not the same.
Therefore [latex]\dfrac{4}{7}\neq \dfrac{5}{9}[/latex]
Example M
Compare [latex]\dfrac{2}{3}[/latex] and [latex]\dfrac{12}{18}[/latex]

- [latex]2 \times 18 = 36[/latex]
- [latex]3 \times 12 = 36[/latex]
- The products 36 and 36 are the same
Therefore [latex]\dfrac{2}{3}= \dfrac{12}{18}[/latex]
Example N
Compare [latex]\dfrac{24}{40}[/latex] and [latex]\dfrac{4}{10}[/latex]
- [latex]24 \times 10 = 240[/latex]
- [latex]40 \times 4 = 160[/latex]
- The products 240 and 160 are not the same.
Therefore [latex]\dfrac{24}{40} \neq \dfrac{4}{10}[/latex]
Exercise 4
State if each pair is equivalent (=) or not equivalent (≠). Use whichever method you wish to find the answer.
- [latex]\dfrac{5}{6}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{30}{60}[/latex]
- [latex]\dfrac{12}{24}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{1}{2}[/latex]
- [latex]\dfrac{6}{7}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{7}{8}[/latex]
- [latex]\dfrac{2}{3}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{12}{18}[/latex]
- [latex]\dfrac{1}{3}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{24}{72}[/latex]
- [latex]\dfrac{3}{4}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{15}{20}[/latex]
- [latex]\dfrac{12}{14}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{6}{7}[/latex]
- [latex]\dfrac{4}{10}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{20}{50}[/latex]
- [latex]\dfrac{5}{10}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{7}{14}[/latex]
Answers to Exercise 4
- ≠
- =
- ≠
- =
- =
- =
- =
- =
- =
Rounding Common Fractions to Whole Numbers
When rounding a fraction to the nearest whole number, if the fraction is less than ½, do not increase to the next whole number.
Examples:
- [latex]2\dfrac{4}{7}≈ 2[/latex]
- [latex]23\dfrac{1}{3} ≈ 23[/latex]
- [latex]\dfrac{1}{4} ≈ 0[/latex]
- [latex]5\dfrac{3}{8}≈ 5[/latex]
Values on either side of a ≈ symbol are approximately or almost equal to each other. The ≈ symbol is similar to the equals sign (=), except the equals sign is used for values that are exactly equal.
If the fraction is ½ or more, consider the fraction as another one which must be added to the whole number:
Examples:
- [latex]2\dfrac{1}{2}≈ 3[/latex]
- [latex]15\dfrac{4}{5}≈ 16[/latex]
- [latex]6\dfrac{7}{8}≈ 7[/latex]
- [latex]\dfrac{3}{4}≈ 1[/latex]
If you are not sure if a fraction is more or less than ½, you can compare it to ½ by making equivalent fractions with a common denominator.
Reminder: greater > smaller
Example O
Round [latex]\dfrac{2}{3}[/latex] to the nearest whole number.
Is [latex]\dfrac{2}{3}>\dfrac{1}{2}[/latex]?
[latex]\dfrac{2}{3}= \dfrac{4}{6}\text{ and }\dfrac{1}{2}= \dfrac{3}{6}[/latex]
YES! [latex]\dfrac{2}{3}[/latex] > [latex]\dfrac{1}{2}\text{ so }\dfrac{2}{3}≈ 1[/latex]
Example P
Round [latex]2\dfrac{4}{7}[/latex] to the nearest whole number.
Is [latex]\dfrac{4}{7} >\dfrac{1}{2}[/latex]?
[latex]\dfrac{4}{7}= \dfrac{8}{14}\text{ and }\dfrac{1}{2} = \dfrac{7}{14}[/latex]
YES! [latex]\dfrac{4}{7}>\dfrac{1}{2}\text{ so }2\dfrac{4}{7}≈3[/latex]
Exercise 5
Round to the nearest whole number.
- [latex]\dfrac{4}{5}≈ 1[/latex]
- [latex]2\dfrac{1}{3}≈ 2[/latex]
- [latex]18\dfrac{1}{2} ≈[/latex]
- [latex]3\dfrac{7}{8} ≈[/latex]
- [latex]9\dfrac{9}{10} ≈[/latex]
- [latex]\dfrac{1}{8} ≈[/latex]
- [latex]4\dfrac{1}{6} ≈[/latex]
- [latex]12\dfrac{7}{9} ≈[/latex]
- [latex]6\dfrac{3}{5} ≈[/latex]
- [latex]20\dfrac{3}{7} ≈[/latex]
- [latex]\dfrac{13}{15} ≈[/latex]
- [latex]99\dfrac{2}{3} ≈[/latex]
Answers to Exercise Five
- 19
- 4
- 10
- 0
- 4
- 13
- 7
- 20
- 1
- 100
Topic A: Self-Test
Mark /25 Aim 20/25
- Define (3 marks)
-
- equivalent
- prime number
- greatest common factor (GCF)
-
- Complete the chart (5 marks).
Factors Common Factors Greatest Common Factor 12
1815
307
286
1618
27 - Express in lowest terms. (6 marks)
- [latex]\dfrac{10}{15}[/latex]= .
- [latex]\dfrac{14}{16}[/latex]= .
- [latex]\dfrac{8}{12}[/latex]= .
- State if each pair of fractions is equivalent (=) or not equivalent (≠). (6 marks)
- [latex]\dfrac{5}{9}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{15}{27}[/latex]
- [latex]\dfrac{3}{7}\hspace{0.25em}\text{?}\hspace{0.25em}\dfrac{15}{35}[/latex]
- Round to the nearest whole number (5 marks)
- 4[latex]\dfrac{5}{8}[/latex] ≈
- 19[latex]\dfrac{4}{10}[/latex] ≈
- [latex]\dfrac{1}{2}[/latex] ≈
- 6[latex]\dfrac{3}{4}[/latex] ≈
- [latex]\dfrac{1}{3}[/latex] ≈
Answers to Topic A Self-Test
- Check your definitions in the glossary.
- Complete the chart.
Factors Common Factors Greatest Common Factor 12
18… of 12 are 1, 2, 3, 4, 6, 12
… of 18 are 1, 2, 3, 6, 9, 182, 3, 6 6 15
30… of 15 are 1, 3, 5, 15 … of 30 are 1, 2, 3, 5, 6, 10, 15, 30
3, 5, 15 15 7
28… of 7 are 1, 7
… of 28 are 1, 2, 4, 7, 14, 287 7 6
16… of 6 are 1, 2, 3, 6
… of 16 are 1, 2, 4, 8, 162 2 18
27… of 18 are 1, 2, 3, 6, 9, 18
… of 27 are 1, 3, 9, 273, 9 9 - Express in lowest terms.
- [latex]\dfrac{2}{5}[/latex]
- [latex]\dfrac{7}{8}[/latex]
- [latex]\dfrac{2}{3}[/latex]
- State if each pair of fractions is equivalent (=) or not equivalent (≠).
- =
- =
- Round to the nearest whole number.
- 5
- 19
- 1
- 7
- 0
The numbers or quantities that are multiplied together to form a given product. 5 × 2 = 10, so 5 and 2 are factors of 10.
The result of a multiplying question, the answer.
A number that can only be divided evenly by itself and 1.
See reduce.
Write a common fraction in lowest terms. Divide both terms by same factor.
In a proportion, multiply the numerator of the first fraction times the denominator of the second fraction. Then multiply the denominator of the first fraction times the numerator of the second fraction. In a true proportion, the products of the cross multiplication are equal.

