Unit 5: Common Fractions & Decimals

Book Five Final Review

You will now practice all the skills you learned in Book 5. You can use this as a review for your final test.

If you can’t remember how to do a question, go back to the lesson on this topic to refresh your memory. The unit and topic for where each question came from is listed next to the question.

Example: 1A means Unit 1, Topic A

1-A

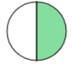
  1. Write in lowest terms the common fractions to describe the shaded portion of each shape.
  1. Draw your own fractions.
    1. [latex]\dfrac{1}{5}[/latex]
    2. [latex]\dfrac{3}{7}[/latex]
  2. Answer the questions using a common fraction, in lowest terms.
    1. Rattan ran for 40 minutes. What fraction of an hour did he run?
    2. Oliver answered 23 of the 27 questions on his test. What fraction of questions did he answer?
    3. Belle got 49 marks on the test. The test was out of 56. What was her score?

1-B

  1. Identify each fraction by writing: proper fraction, improper fraction, or mixed number next to each fraction.
    1. [latex]\dfrac{5}{2}[/latex]
    2. [latex]2\dfrac{1}{3}[/latex]
    3. [latex]\dfrac{4}{5}[/latex]
    4. [latex]\dfrac{7}{3}[/latex]
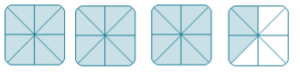
  2. Write the improper fraction and the equivalent mixed number that describe the shaded part in each drawing.
  3. Rename each improper fraction into a mixed number.
    1. [latex]\dfrac{11}{5} =[/latex]
    2. [latex]\dfrac{15}{4} =[/latex]
    3. [latex]\dfrac{19}{6} =[/latex]
  4. Rename each whole number as an improper fraction. Use the denominator given to you.
    1. [latex]5=\dfrac{ }{2}[/latex]
    2. [latex]3=\dfrac{ }{5}[/latex]
    3. [latex]8=\dfrac{ }{3}[/latex]
  5. Rename each mixed number as an improper fraction
    1. [latex]2\dfrac{3}{8} =[/latex]
    2. [latex]6\dfrac{5}{9} =[/latex]
    3. [latex]1\dfrac{2}{3} =[/latex]

2-A

  1. Find the factors, common factors and the Greatest Common Factor (GCF) Fraction Factors Common Factors GCF
    1. [latex]\dfrac{4}{22}[/latex]
    2. [latex]\dfrac{12}{48}[/latex]
    3. [latex]\dfrac{27}{36}[/latex]
    4. [latex]\dfrac{12}{40}[/latex]
  2. Express each fraction in lowest terms.
    1. [latex]\dfrac{7}{21} =[/latex]
    2. [latex]\dfrac{9}{24} =[/latex]
    3. [latex]\dfrac{10}{250} =[/latex]
    4. [latex]\dfrac{12}{36} =[/latex]
  3. State if each pair of fractions is equivalent (=) or not equivalent (≠) by placing the correct sign between them.
    1. [latex]\dfrac{3}{4}[/latex]                  [latex]\dfrac{31}{42}[/latex]
    2. [latex]\dfrac{1}{7}[/latex]                  [latex]\dfrac{5}{35}[/latex]
    3. [latex]\dfrac{4}{13}[/latex]                  [latex]\dfrac{6}{39}[/latex]
    4. [latex]\dfrac{1}{3}[/latex]                   [latex]\dfrac{11}{13}[/latex]
  4. Round to the nearest whole number.
    1. [latex]2\dfrac{1}{6} =[/latex]
    2. [latex]1\dfrac{4}{5} =[/latex]
    3. [latex]\dfrac{3}{5} =[/latex]

3-A

  1. Write the multiplication equation you would use to find the answer to the question. Do not calculate the answer.
    1. Joan peeled [latex]\tfrac{3}{4}[/latex] of the 35 kilograms of apples. How many kilograms of apples did Joan peel?
    2. There are 16 bottles of ketchup in the restaurant. They are each full. How many full bottles of ketchup would there be if all ketchup bottles were put together?
    3. Half a recipe that needs [latex]2\dfrac{2}{3}[/latex]cups of sugar.
    4. The community pool has a capacity of 150 swimmers. The pool is full. How many swimmers are there?
  2. Find the products. Make sure your answers are in lowest terms.
    1. [latex]\dfrac{1}{3}\times\dfrac{4}{5} =[/latex]
    2. [latex]\dfrac{1}{3}\text{ of }34 =[/latex]
    3. [latex]4\times\dfrac{3}{5} =[/latex]
    4. [latex]\dfrac{5}{7}\text{ of }1\dfrac{1}{5} =[/latex]
    5. [latex]2\dfrac{1}{2}\times7\dfrac{1}{2} =[/latex]
    6. [latex]\dfrac{3}{4}\times\dfrac{1}{7}\times4\dfrac{5}{9} =[/latex]
  3. Solve the following word problems.
    1. Emma saves [latex]\tfrac{1}{5}[/latex] of her income for the down payment on a house. If her annual income is $34458.00, how much can she save in one year?
    2. [latex]\tfrac{1}{3}[/latex]of the students at one Vancouver college speaks a language other than English. [latex]\tfrac{3}{4}[/latex] of those students are enrolled in English Language Learning (ELL). What fraction of the students are studying ELL?
    3. A recipe calls for [latex]1\tfrac{1}{2}[/latex] cups of sugar. How much sugar should be used if the recipe is being tripled?
    4. Find the area of the rectangle.
    5. A corner store sells 2345 items in one day. [latex]\tfrac{4}{5}[/latex] of those items are junk food. How many of those items are junk food?
  4. Divide the following fractions. Show all your work, and make sure your answers are in the lowest terms.
    1. [latex]\dfrac{1}{3}÷\dfrac{3}{4} =[/latex]
    2. [latex]\dfrac{1}{2}÷\dfrac{3}{5} =[/latex]
    3. [latex]\dfrac{3}{5}÷ 9 =[/latex]
    4. [latex]3\dfrac{2}{3}÷\dfrac{1}{2} =[/latex]
    5. [latex]5\dfrac{1}{5}÷\dfrac{6}{7} =[/latex]
    6. [latex]4\dfrac{1}{3}÷2\dfrac{2}{5} =[/latex]
  5. Solve the following word problems:
    1. Kathy worked on planting garlic last weekend. It took her [latex]3\tfrac{1}{2}[/latex] minutes to plant one row. How many rows did she plant in [latex]\tfrac{1}{3}[/latex] of an hour? (one hour = 60 minutes)
    2. Nicole knits socks in the evenings. It takes her [latex]7\tfrac{1}{3}[/latex] hours to knit one sock. How many hours does it take to knit a pair of socks (that is 2 socks)?
    3. Last week Nicole knit for a total of [latex]27\tfrac{1}{2}[/latex] hours. Approximately how many socks could she knit in that time? (To get an approximate, round your numbers to whole numbers first).
    4. A baking sheet is [latex]39\tfrac{3}{5}[/latex] cm by [latex]18\tfrac{1}{4}[/latex] cm. Find its area.

4-A

  1. Add these common fractions. Make sure to reduce your answer to the lowest terms.
    1. [latex]\begin{array}{rr}&\dfrac{1}{5}\\+&\dfrac{4}{5}\\\hline\end{array}[/latex]
    2. [latex]\begin{array}{rr}&\dfrac{3}{5}\\+&\dfrac{6}{7}\\\hline\end{array}[/latex]
    3. [latex]\dfrac{2}{7} + \dfrac{3}{4} =[/latex]
    4. [latex]\dfrac{2}{3} + \dfrac{5}{9} =[/latex]
    5. [latex]\begin{array}{rr}&\dfrac{5}{12}\\+&\dfrac{5}{8}\\\hline\end{array}[/latex]
    6. [latex]\begin{array}{rr}&\dfrac{2}{3}\\+&\dfrac{5}{6}\\\hline\end{array}[/latex]
  2. Add these mixed numbers, express the sum in the lowest terms.
    1. [latex]\begin{array}{rr}&4\dfrac{2}{5}\\+&7\dfrac{4}{7}\\\hline\end{array}[/latex]
    2. [latex]2\dfrac{1}{3} + 4\dfrac{3}{4} =[/latex]
    3. [latex]1\dfrac{2}{3} + 3\dfrac{1}{2} + 3\dfrac{3}{4} =[/latex]
    4. [latex]4\dfrac{1}{8} + 1\dfrac{1}{4} =[/latex]
    5. [latex]\begin{array}{rr}&4\dfrac{1}{9}\\+&2\dfrac{2}{3}\\\hline\end{array}[/latex]
    6. [latex]\begin{array}{rr}&2\dfrac{7}{15}\\+&10\dfrac{1}{5}\\\hline\end{array}[/latex]
  3. Subtract these common fractions, express the sum in the lowest terms.
    1. [latex]\begin{array}{rr}&\dfrac{5}{12}\\−&\dfrac{1}{3}\\\hline\end{array}[/latex]
    2. [latex]\begin{array}{rr}&\dfrac{5}{6}\\−&\dfrac{3}{4}\\\hline\end{array}[/latex]
    3. [latex]\begin{array}{rr}&\dfrac{1}{2}\\−&\dfrac{9}{24}\\\hline\end{array}[/latex]
    4. [latex]\dfrac{4}{5} − \dfrac{1}{4} =[/latex]
    5. [latex]\dfrac{30}{35} − \dfrac{2}{5} =[/latex]
    6. [latex]\dfrac{1}{2} − \dfrac{5}{12} =[/latex]
  4. Subtract these mixed numbers, express the sum in the lowest terms.
    1. [latex]\begin{array}{rr}&7\dfrac{2}{3}\\−&2\dfrac{1}{6}\\\hline\end{array}[/latex]
    2. [latex]\begin{array}{rr}&2\dfrac{4}{7}\\−&1\dfrac{5}{21}\\\hline\end{array}[/latex]
    3. [latex]\begin{array}{rr}&9\dfrac{1}{5}\\−&4\dfrac{4}{25}\\\hline\end{array}[/latex]
    4. [latex]3\dfrac{1}{2} − 1\dfrac{4}{7} =[/latex]
    5. [latex]6\dfrac{1}{2} − 3\dfrac{3}{4} =[/latex]
    6. [latex]5\dfrac{1}{2} − 2\dfrac{7}{8} =[/latex]
  5. Solve the following word problems.
    1. A concrete contractor needs [latex]6\tfrac{1}{3}[/latex] metres of wire mesh for a concrete walkway and [latex]12\tfrac{3}{8}[/latex] metres of wire mesh for a driveway. If the contractor starts with a roll that is [latex]54\tfrac{1}{4}[/latex] metres long, how much wire mesh is left at the end of the two jobs?
    2. Frida and Sean collect returnable bottles and cans. Frida has [latex]3\tfrac{1}{3}[/latex] bags of returnables. Sean has [latex]4\tfrac{1}{2}[/latex] bags to return. How much more does Sean have than Frida?
    3. Mike bought [latex]5\tfrac{1}{4}[/latex] metres of cotton to sew three shirts. Each shirt took [latex]1\tfrac{3}{5}[/latex] m of material. How much cotton is left over?
    4. A freight container is loaded with 3 groups of products. Group A weighs [latex]58\tfrac{1}{2}[/latex] tons, Group B weighs [latex]23\tfrac{5}{8}[/latex] tons and Group C weighs [latex]29\tfrac{1}{4}[/latex] tons. Find the weight of the products.
    5. If the loaded container is question d) is [latex]189\tfrac{3}{5}[/latex] tons, what is the weight of the empty container?

5-A

  1. Write as a common fraction in lowest terms.
    1. 0.75
    2. 0.16
    3. 0.1
    4. 0.4
    5. 1.6
    6. 2.625
    7. 3.3
    8. 0.125
  2. Write as decimals. Round your answer to 3 decimal places.
    1. [latex]\dfrac{3}{8}[/latex]
    2. [latex]\dfrac{1}{3}[/latex]
    3. [latex]\dfrac{3}{4}[/latex]
    4. [latex]\dfrac{1}{20}[/latex]
    5. [latex]\dfrac{1}{8}[/latex]
    6. [latex]1\dfrac{2}{3}[/latex]
    7. [latex]\dfrac{1}{5}[/latex]
    8. [latex]\dfrac{6}{6}[/latex]
  3. Compare the following fractions, use <  or  >.
    1. [latex]\dfrac{2}{3}[/latex]                  [latex]\dfrac{1}{4}[/latex]
    2. [latex]\dfrac{2}{5}[/latex]                  [latex]\dfrac{4}{7}[/latex]
    3. [latex]\dfrac{5}{9}[/latex]                  [latex]\dfrac{1}{3}[/latex]
    4. [latex]\dfrac{7}{12}[/latex]                  [latex]\dfrac{2}{3}[/latex]
  4. Compare the following fractions to decimals. Use < , >, or =.
    1. [latex]\dfrac{1}{2}[/latex]                  [latex]0.5[/latex]
    2. [latex]\dfrac{2}{3}[/latex]                  [latex]0.625[/latex]
    3. [latex]0.125[/latex]                  [latex]\dfrac{1}{8}[/latex]
    4. [latex]\dfrac{4}{9}[/latex]                  [latex]0.6[/latex]
    5. [latex]3.45[/latex]                  [latex]\dfrac{1}{8}[/latex]
    6. [latex]\dfrac{1}{5}[/latex]                  [latex]0.3[/latex]

Answers to Book Five Final Review

  1. Write in lowest terms the common fractions to describe the shaded portion of each shape.
    1.  [latex]\dfrac{3}{4}[/latex]
    2. [latex]\dfrac{1}{4}[/latex]
    3. [latex]\dfrac{1}{2}[/latex]
  2. Draw your own fractions.
    1. A shape with five parts. One part is coloured in.
    2. A shape with seven parts. Three parts are coloured in.
  3. Answer the questions using a common fraction, in lowest terms.
    1.  [latex]\dfrac{2}{3}[/latex]
    2. [latex]\dfrac{23}{27}[/latex]
    3. [latex]\dfrac{7}{8}[/latex]
  4. Identify each fraction by writing: proper fraction, improper fraction, or mixed number next to each fraction.
    1. improper fraction
    2. mixed number
    3. proper fraction
    4. improper fraction
  5. Write the improper fraction and the equivalent mixed number that describe the shaded part in each drawing.
    1. [latex]\dfrac{27}{8}[/latex],  [latex]3\dfrac{3}{8}[/latex]
    2. [latex]\dfrac{13}{4}[/latex],  [latex]3\dfrac{1}{4}[/latex]
  6. Rename each improper fraction into a mixed number.
    1.  [latex]2\dfrac{1}{5}[/latex]
    2. [latex]3\dfrac{3}{4}[/latex]
    3. [latex]3\dfrac{1}{6}[/latex]
  7. Rename each whole number as an improper fraction. Use the denominator given to you.
    1. [latex]\dfrac{10}{2}[/latex]
    2. [latex]\dfrac{15}{5}[/latex]
    3. [latex]\dfrac{24}{3}[/latex]
  8. Rename each mixed number as an improper fraction.
    1. [latex]\dfrac{19}{8}[/latex]
    2. [latex]\dfrac{59}{9}[/latex]
    3. [latex]\dfrac{5}{3}[/latex]
  9. Find the factors, common factors and the Greatest Common Factor (G.C.F.).
    Fraction Factors Common Factors G.C.F.
    a [latex]\dfrac{4}{22}[/latex] 1, 2, 4

    1, 2, 11, 22

    		 2 2
    b [latex]\dfrac{12}{48}[/latex] 1, 2, 3, 4, 6, 12

    1, 2, 3, 4, 6, 8, 12, 16, 24, 48

    		 2, 3, 4, 6, 12 12
    c [latex]\dfrac{27}{36}[/latex] 1, 3, 9, 27

    1, 2, 3, 4, 6, 9, 12, 18, 36

    		 3, 9 9
    d [latex]\dfrac{12}{40}[/latex] 1, 2, 3, 4, 6, 12

    1, 2, 4, 5, 8, 10, 20, 40

    		 2, 4 4
  10. Express each fraction in lowest terms.
    1. [latex]\dfrac{1}{3}[/latex]
    2. [latex]\dfrac{3}{8}[/latex]
    3. [latex]\dfrac{1}{25}[/latex]
    4. [latex]\dfrac{1}{3}[/latex]
  11. State if each pair of fractions is equivalent (=) or not equivalent (≠) by placing the correct sign between them.
    1. ≠
    2. =
    3. ≠
    4. ≠
  12. Round to the nearest whole number.
    1. 2
    2. 2
    3. 1
  13. Write the multiplication equation you would use to find the answer to the question.
    1. [latex]\dfrac{3}{4}\times\dfrac{35}{1}[/latex]
    2. [latex]16\times\dfrac{1}{4}[/latex]
    3. [latex]\dfrac{1}{2}\times\dfrac{22}{3}[/latex]
    4. [latex]150\times\dfrac{1}{5}[/latex]
  14. Find the products. Make sure your answers are in lowest terms.
    1. [latex]\dfrac{4}{15}[/latex]
    2. [latex]11\dfrac{1}{3}[/latex]
    3. [latex]2\dfrac{2}{5}[/latex]
    4. [latex]\dfrac{6}{7}[/latex]
    5. [latex]18\dfrac{3}{4}[/latex]
    6. [latex]\dfrac{41}{84}[/latex]
  15. Solve the following word problems.
    1. $6891[latex]\tfrac{3}{5}[/latex]
    2. [latex]\tfrac{1}{4}[/latex]
    3. [latex]4\tfrac{1}{2}[/latex] cups
    4. [latex]\tfrac{1}{6}[/latex] m2
    5. 1876
  16. Divide the following fractions. Show all your work, and make sure your answers are in the lowest terms.
    1. [latex]\dfrac{4}{9}[/latex]
    2. [latex]\dfrac{5}{6}[/latex]
    3. [latex]\dfrac{1}{15}[/latex]
    4. [latex]7\dfrac{1}{3}[/latex]
    5. [latex]6\dfrac{1}{15}[/latex]
    6. [latex]1\dfrac{29}{36}[/latex]
  17. Solve the following word problems.
    1. [latex]5\tfrac{5}{7}[/latex] rows
    2. [latex]14\tfrac{2}{3}[/latex] hours
    3. [latex]4[/latex] socks
    4. [latex]8\tfrac{2}{3}[/latex] km
    5. [latex]722\tfrac{7}{10}[/latex] cm2
  18. Add these common fractions, make sure to reduce your answer to the lowest terms.
    1. [latex]1[/latex]
    2. [latex]1\dfrac{16}{35}[/latex]
    3. [latex]1\dfrac{1}{28}[/latex]
    4. [latex]1\dfrac{2}{9}[/latex]
    5. [latex]1\dfrac{1}{24}[/latex]
    6. [latex]1\dfrac{1}{2}[/latex]
  19. Add these mixed numbers, express the sum in the lowest terms.
    1. [latex]11\dfrac{34}{35}[/latex]
    2. [latex]7\dfrac{1}{12}[/latex]
    3. [latex]8\dfrac{11}{12}[/latex]
    4. [latex]5\dfrac{3}{8}[/latex]
    5. [latex]6\dfrac{7}{9}[/latex]
    6. [latex]12\dfrac{2}{3}[/latex]
  20. Subtract these common fractions. Express your answer in lowest terms.
    1. [latex]\dfrac{1}{12}[/latex]
    2. [latex]\dfrac{1}{12}[/latex]
    3. [latex]\dfrac{1}{8}[/latex]
    4. [latex]\dfrac{11}{20}[/latex]
    5. [latex]\dfrac{16}{35}[/latex]
    6. [latex]\dfrac{1}{12}[/latex]
  21. Subtract these mixed numbers, express your answer in lowest terms.
    1. [latex]5\dfrac{1}{2}[/latex]
    2. [latex]1\dfrac{1}{3}[/latex]
    3. [latex]5\dfrac{1}{25}[/latex]
    4. [latex]1\dfrac{13}{14}[/latex]
    5. [latex]2\dfrac{3}{8}[/latex]
    6. [latex]2\dfrac{5}{8}[/latex]
  22. Solve the following word problems.
    1. [latex]35\tfrac{13}{24}[/latex] m
    2. [latex]1\tfrac{1}{6}[/latex] more
    3. [latex]\tfrac{9}{20}[/latex] metres
    4. [latex]111\tfrac{3}{8}[/latex] tonnes
    5. [latex]78\tfrac{3}{8}[/latex] tonnes
  23. Write as a common fraction in lowest terms.
    1. [latex]\dfrac{3}{4}[/latex]
    2. [latex]\dfrac{1}{6}[/latex]
    3. [latex]\dfrac{1}{10}[/latex]
    4. [latex]\dfrac{2}{5}[/latex]
    5. [latex]1\dfrac{3}{5}[/latex]
    6. [latex]2\dfrac{5}{8}[/latex]
    7. [latex]3\dfrac{1}{3}[/latex]
    8. [latex]\dfrac{1}{8}[/latex]
  24. Write as decimals. Round your answer to 3 decimal places.
    1. [latex]0.375[/latex]
    2. [latex]0.\overline{3}[/latex]
    3. [latex]0.75[/latex]
    4. [latex]0.05[/latex]
    5. [latex]0.125[/latex]
    6. [latex]1.\overline{6}[/latex]
    7. [latex]0.2[/latex]
    8. [latex]1[/latex]
  25. Compare the following fractions, use < or >.
    1. >
    2. <
    3. >
    4. <
  26. Compare the following fractions to decimals. Use < , >, or =.
    1. =
    2. >
    3. =
    4. <
    5. >
    6. <

License

Icon for the Creative Commons Attribution 4.0 International License

Adult Literacy Fundamental Mathematics: Book 5 - 2nd Edition Copyright © 2023 by Liz Girard; Wendy Tagami; and Leanne Caillier-Smith is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book