"

Unit 2: Percent

Topic A: Introducing Percent

Reading and Writing Percents

To write a percent:

  • Write the number in the usual way
  • Place the percent sign after the numerals
    • [latex]50\%[/latex]
    • [latex]5\frac{1}{2}\%[/latex] or [latex]5.5\%[/latex]
    • [latex]\frac{3}{4}\%[/latex] or [latex]0.75\%[/latex]

To read a percent:

  • Read the numbers in the usual way
  • Say “percent” after the number
    • [latex]16\%[/latex]: say “sixteen percent”
    • [latex]4\frac{1}{2}\%[/latex]: say “four and one-half percent”
    • [latex]0.25\%[/latex]: say “twenty-five hundredths percent,” or “one-quarter percent,” or “point two five percent”

Exercise 1

Write these percents using numerals and a percent sign. Note that the mixed numbers may be expressed with common fractions or decimals.

  1. Thirty-four percent          [latex]34\%[/latex]
  2. Twelve percent
  3. Four-fifths percent
  4. One hundred sixteen and three-tenths percent
  5. Thirteen percent
  6. Six and one-fifth percent
  7. Ninety-four and one-half percent

Answers to Exercise 1

  1. [latex]12\%[/latex]
  2. [latex]0.8\%[/latex] or [latex]\frac{4}{5}\%[/latex]
  3. [latex]116.3\%[/latex] or [latex]116\frac{3}{10}\%[/latex]
  4. [latex]13\%[/latex]
  5. [latex]6.2\%[/latex] or [latex]6\frac{1}{5}\%[/latex]
  6. [latex]94.5\%[/latex] or [latex]94\frac{1}{2}\%[/latex]

Exercise 2

Write these percents using words.

  1. [latex]62\%[/latex]: sixty-two percent
  2. [latex]37\frac{1}{2}\%[/latex]
  3. [latex]202\%[/latex]
  4. [latex]\frac{3}{4}\%[/latex]
  5. [latex]18.3\%[/latex]
  6. [latex]14\frac{1}{2}\%[/latex]
  7. [latex]100\frac{1}{2}\%[/latex]

Answers to Exercise 2

  1. Thirty-seven and one-half percent
  2. Two hundred two percent
  3. Three-quarters percent
  4. Eighteen and three-tenths percent
  5. Fourteen and one-half percent
  6. One hundred one percent

Changing Decimals to Percents

Writing equivalent fractions is an important math skill.

Equivalent common fractions, decimals, and percents all represent the same amount.

Equivalent fractions, decimals, and percentages
Fractions Decimals Percentages
[latex]\frac{1}{2}[/latex] [latex]0.5[/latex] [latex]50\%[/latex]
[latex]\frac{3}{10}[/latex] [latex]0.3[/latex] [latex]30\%[/latex]

You need the skill of writing equivalent fractions for working with percents.

To change any number to a percent, multiply the number by 100% and place a percent sign % after the product.

Remember this shortcut for multiplying by 100?

[latex]4.27\times100=427[/latex]
[latex]0.287\times100=28.7[/latex]
[latex]53\times100=5300[/latex]

The shortcut is: When multiplying by 100, move the decimal point two places to the right.

Example A

Change these numbers to a percent.
[latex]\begin{equation}\begin{split} &1 \ \ \ \ \ \ \ \ &1\times100\% \ \ \ \ &= \ \ \ \ &100\% \\ &0.25 \ \ \ \ \ \ \ &0.25\times100\% \ \ \ \ &= \ \ \ \ &25\% \\ &0.8 \ \ \ \ \ \ \ &0.8\times100\% \ \ \ \ &= \ \ \ \ &80\% \\ &0.375 \ \ \ \ \ \ \ &0.375\times100\% \ \ \ \ &= \ \ \ \ &37.5\% \\ \end{split}\end{equation}[/latex]

So…

To change a decimal to a percent, move the decimal point two places to the right and then write the percent sign after the number.

Example B

Change each decimal to a percent.
[latex]\begin{equation}\begin{split} &\curvearrowright \\ 0.125=0&.125=12.5\% \end{split}\end{equation}[/latex]
[latex]\begin{equation}\begin{split} &\curvearrowright \\ 1.375=1&.375=137.5\% \end{split}\end{equation}[/latex]

If the decimal point moves to the end of the number it is not necessary to write the decimal point. Remember that zeros at the beginning of a number are also not necessary.

[latex]\begin{equation}\begin{split} &\curvearrowright \\ 0.24=0&.24=\cancel{0.}24\%=24\% \end{split}\end{equation}[/latex]

[latex]\begin{equation}\begin{split} &\curvearrowright \\ 0.05=0&.05=\cancel{0.0}5\%=5\% \end{split}\end{equation}[/latex]

If the decimal is a tenth (one decimal place), it will be necessary to add a zero. If you are changing a whole number to a percent, add two zeros.

[latex]\begin{equation}\begin{split} &\curvearrowright \\ 0.4=0&.40=40\% \end{split}\end{equation}[/latex]

[latex]\begin{equation}\begin{split} &\curvearrowright \\ 1.7=1&.70=170\% \end{split}\end{equation}[/latex]

[latex]\begin{equation}\begin{split} &\curvearrowright \\ 2=2&.00=200\% \end{split}\end{equation}[/latex]

Exercise 3

Change these decimals to percents.

Decimal × 100%
Move decimal 2 places to right		 = Percent
A. [latex]0.75[/latex] [latex]\begin{equation}\begin{split} &\curvearrowright \\ 0&.75 \end{split}\end{equation}[/latex] [latex]=75\%[/latex]
B. [latex]0.33[/latex]
C. [latex]0.1[/latex]
D. [latex]0.0025[/latex]
E. [latex]0.9[/latex]
F. [latex]0.325[/latex]
G. [latex]0.0625[/latex]
H. [latex]3[/latex]

Answers to Exercise 3

  1. [latex]33\%[/latex]
  2. [latex]10\%[/latex]
  3. [latex]0.25\%[/latex]
  4. [latex]90\%[/latex]
  5. [latex]32.5\%[/latex]
  6. [latex]6.25\%[/latex]
  7. [latex]300\%[/latex]

Changing Percents to Decimals

Review dividing by 100:

[latex]47.39\div100=0.4739[/latex]
[latex]429\div100=4.29[/latex]
[latex]3.824\div100=0.03824[/latex]

To divide by 100, move the decimal point two places to the left.

Example A

Change each percent to a decimal or mixed number.

[latex]\begin{equation}\begin{split} 58\% \ \ &= \ \ 58\div100 \ \ &= \ \ .58 \ \ &= \ \ 0.58 \\ 20\% \ \ &= \ \ 20\div100 \ \ &= \ \ .2 \ \ &= \ \ 0.2 \\ 6\% \ \ &= \ \ 6\div100 \ \ &= \ \ .06 \ \ &= \ \ 0.06 \\ 110\% \ \ &= \ \ 110\div100 \ \ &= \ \ 1.10 \end{split}\end{equation}[/latex]

So…

To change a percent to a decimal, divide by 100 (move the decimal point two places to the left) and remove the percent sign.

Example B

Change each percent to a decimal.

[latex]\begin{equation}\begin{split} 75\% \ \ &= \ \ 75.0\% \ \ &= \ \ 0.75 \\ 12\% \ \ &= \ \ 12.0\% \ \ &= \ \ 0.12 \\ 37.5\% \ \ &= \ \ 37.5\% \ \ &= \ \ 0.375 \\ 125\% \ \ &= \ \ 125.0\% \ \ &= \ \ 1.25 \\ 5\% \ \ &= \ \ 5.0\% \ \ &= \ \ 0.05 \\ 4.6\% \ \ &= \ \ 4.6\% \ \ &= \ \ 0.046 \\ \end{split}\end{equation}[/latex]

Some notes to remember:

  • If there is no decimal point in the percent, place the decimal point after the last numeral and then divide by 100. [latex]24\%=24.0\%=0.24[/latex]
  • It may be necessary to prefix zeros. (This means adding zeros in front of the number, if needed). [latex]6\%=6.0\%=0.06[/latex]
  • A zero at the right of a decimal is not needed and may be left off. [latex]40\%=40.0\%=0.40=0.4[/latex]

Exercise 4

Change each percent to its decimal equivalent.

Percent ÷ 100%
Move decimal 2 places to left		 = Decimal
A. [latex]23\%[/latex] [latex]\begin{equation}\begin{split} &\curvearrowleft \\ & \ 23. \end{split}\end{equation}[/latex] [latex]=0.23[/latex]
B. [latex]1\%[/latex]
C. [latex]112\%[/latex]
D. [latex]10.3\%[/latex]
E. [latex]36\%[/latex]
F. [latex]147\%[/latex]

Answers to Exercise 4

  1. [latex]0.01[/latex]
  2. [latex]1.12[/latex]
  3. [latex]0.103[/latex]
  4. [latex]0.36[/latex]
  5. [latex]1.47[/latex]

To change a percent containing a common fraction to a decimal, do this:

  • Change the common fraction in the percent to a decimal in the percent.
  • Divide by 100 (move the decimal 2 places to the left).

Example C

Let’s convert these percents containing common fractions into decimals:

[latex]\begin{equation}\begin{split} 3\tfrac{1}{2}\% \ \ &= \ \ 3.5\% \ \ \ \ \ \ \ &3.5\% &\div 100 \ &= .035 &= 0.035 \\ 37\tfrac{1}{2}\% \ \ &= \ \ 37.5\% \ \ \ \ \ \ \ &37.5\% &\div 100 \ &= .375 &= 0.375 \\ \tfrac{1}{4}\% \ \ &= \ \ 0.25\% \ \ \ \ \ \ \ &0.25\% &\div 100 \ &= .0025 \\ 17\tfrac{1}{3}\% \ \ &= \ \ 17.\overline{3}\% \ \ \ \ \ \ \ &17.\overline{3}\% &\div 100 \ &= 0.17\overline{3} \end{split}\end{equation}[/latex]

Exercise 5

Change each percent to its decimal equivalent.

  1. [latex]8\frac{4}{5}\%= \ \ \ \ \ 8.8\%=0.088[/latex]
  2. [latex]4\frac{1}{2}\%=[/latex]
  3. [latex]56\frac{3}{4}\%=[/latex]
  4. [latex]1\frac{3}{5}\%=[/latex]
  5. [latex]112\frac{1}{2}\%=[/latex]
  6. [latex]2\frac{3}{8}\%=[/latex]
  7. [latex]5\frac{1}{4}\%=[/latex]

Answers to Exercise 5

  1. [latex]0.045[/latex]
  2. [latex]0.5675[/latex]
  3. [latex]0.016[/latex]
  4. [latex]1.125[/latex]
  5. [latex]0.02375[/latex]
  6. [latex]0.0525[/latex]

Changing Common Fractions to Percents

To change any number to a percent, multiply the number by 100% and place the percent sign % after the product.

There are two methods you can use to change a common fraction to a percent.

Method One

To change a common fraction to an equivalent percent, multiply the common fraction by 100%.

Example A

[latex]\frac{3}{4} = \text{_____}\%[/latex]
[latex]\frac{3}{4}[/latex]
Multiply by 100% [latex]\frac{3}{4} \times 100\%[/latex]
Convert 100% to a fraction. [latex]\frac{3}{4} \times \frac{100}{1}\%[/latex]
Simplify the fractions by dividing the numerator and denominator by 4. [latex]\frac{3}{\cancel{4}1} \times \frac{\cancel{100}25}{1}\%[/latex]
The 4 cancels and 100 is reduced to 25. [latex]\frac{3}{1} \times \frac{25}{1}\%[/latex]
Multiply 3 by 25%. [latex]3 \times 25\%[/latex]
[latex]75\%[/latex]
[latex]1\frac{1}{5} = \text{_____}\%[/latex]
[latex]1\frac{1}{5}[/latex]
Convert number to a fraction. [latex]\frac{6}{5}[/latex]
Multiply by 100%. [latex]\frac{6}{5} \times 100\%[/latex]
Convert 100% to a fraction. [latex]\frac{6}{5} \times \frac{100}{1}\%[/latex]
Simplify the fractions by dividing the denominator and numerator by 5. [latex]\frac{6}{\cancel{5}1} \times \frac{\cancel{100}20}{1}\%[/latex]
The 5 cancels and 100 is reduced to 20. [latex]\frac{6}{1} \times \frac{20}{1}\%[/latex]
Multiply 6 by 20%. [latex]6 \times 20\%[/latex]
[latex]120\%[/latex]

Exercise 6

Multiply by 100% to change each common fraction to an equivalent percent.

  1. [latex]\frac{4}{5} \ \ \ \ \ \ \ \ \ \ \frac{4}{5}\times100\%=80\%[/latex]
  2. [latex]\frac{1}{5}=[/latex]
  3. [latex]\frac{9}{10}=[/latex]
  4. [latex]1\frac{1}{2}=[/latex]
  5. [latex]\frac{7}{10}=[/latex]
  6. [latex]3\frac{3}{4}=[/latex]
  7. [latex]\frac{1}{2}=[/latex]

Answers to Exercise 6

  1. [latex]20\%[/latex]
  2. [latex]90\%[/latex]
  3. [latex]150\%[/latex]
  4. [latex]70\%[/latex]
  5. [latex]375\%[/latex]
  6. [latex]50\%[/latex]

Method Two

To change a common fraction to an equivalent percent, first write the common fraction as a decimal. Then multiply the decimal by 100% (move the decimal point two places to the right).

Example A

  1. [latex]\frac{3}{8}=\text{_____}\%[/latex]
  2. Use long division to write the fraction as a decimal.
  3. [latex]\frac{3}{8}=0.375[/latex]
  4. Move the decimal two spots to the right.
    [latex]\begin{equation}\begin{split}&\curvearrowright \\ 0&.375=37.5\end{split}\end{equation}[/latex]
Convert [latex]\frac{3}{8}[/latex] to a percentage
[latex]\frac{3}{8} = \text{_____}\%[/latex]
Use long division to write fraction as a decimal. 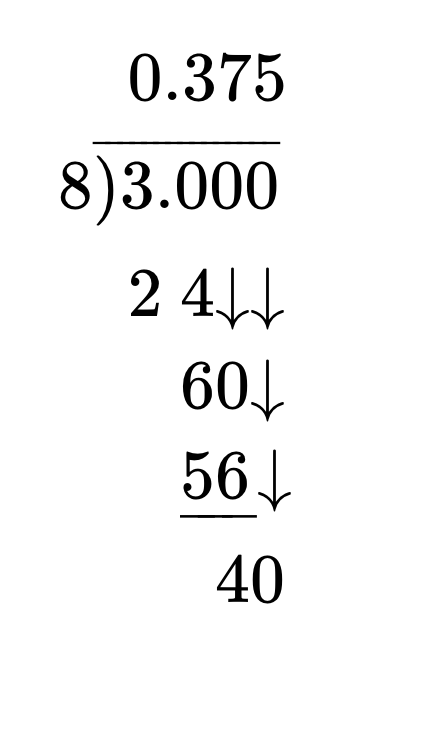A long division equation showing that 3 divided by 8 equals 0.375.
[latex]\frac{3}{8} = 0.375[/latex]
Move the decimal point two places to the right and add the percent sign. [latex]0.375 = 37.5\%[/latex]
Convert [latex]\frac{1}{3}[/latex] to a percentage
[latex]\frac{1}{3} = \text{_____}\%[/latex]
Use long division to write fraction as a decimal. 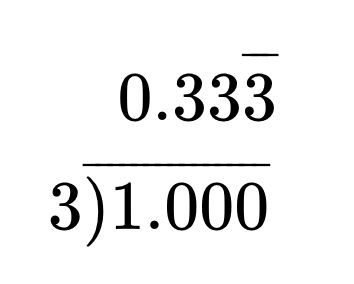A long division equation showing that 1 divided by 3 equals 0.333 repeating.
[latex]\frac{1}{3} = 0.33\overline{3}[/latex]
Move the decimal point two places to the right and add the percent sign. [latex]0.33\overline{3}=33.\overline{3}\% \text{ also written as } 33\frac{1}{3}\%[/latex]
Convert [latex]\frac{11}{12}[/latex] to a percentage
[latex]\frac{11}{12} = \text{_____}\%[/latex]
Use long division to write fraction as a decimal. 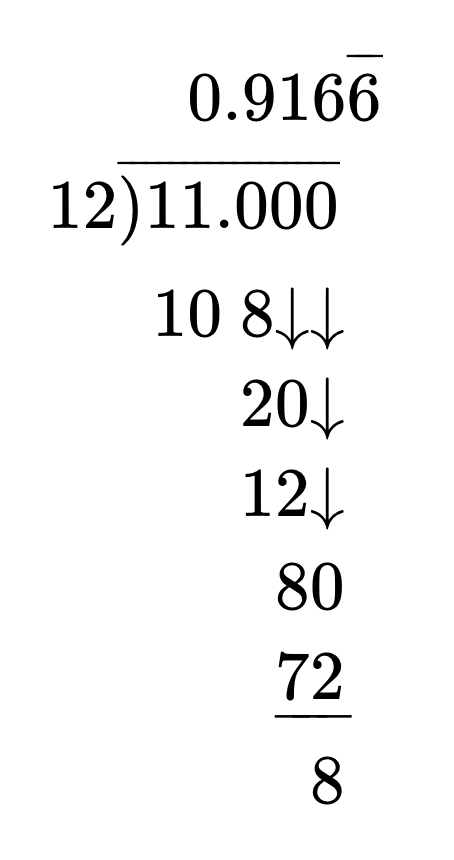A long division equation showing that 11 divided by 12 equals 0.9166 repeating.
[latex]\frac{11}{12} = 0.91\overline{6}[/latex]
 Move the decimal point two places to the right and add the percent sign. [latex]0.916\overline{6} = 91.\overline{6}\%[/latex]

Exercise 7

  1. [latex]\tfrac{1}{12}=0.08\overline{3} \ \ \ \ \ \ 0.08\overline{3}\times100\%=8.\overline{3}\%[/latex]
  2. [latex]\tfrac{1}{8}[/latex]
  3. [latex]\tfrac{5}{8}[/latex]
  4. [latex]\tfrac{7}{8}[/latex]
  5. [latex]\tfrac{2}{3}[/latex]
  6. [latex]\tfrac{5}{16}[/latex]
  7. [latex]\tfrac{5}{6}[/latex]
  8. [latex]\tfrac{4}{9}[/latex]

Answers to Exercise 7

  1. [latex]12.5\%[/latex]
  2. [latex]62.5\%[/latex]
  3. [latex]87.5\%[/latex]
  4. [latex]66.\overline{6}\%[/latex]
  5. [latex]31.25\%[/latex]
  6. [latex]83.\overline{3}\%[/latex]
  7. [latex]44.\overline{4}\%[/latex]

The method you use to change a common fraction to a percent will depend on the numbers you are working with. Choose whichever method seems easier for the situation. You will also memorize many equivalencies as you work with them. But you should definitely memorize:

  • [latex]\tfrac{1}{3}=33\tfrac{1}{3}\%[/latex]
  • [latex]\tfrac{2}{3}=66\tfrac{2}{3}\%[/latex]

Changing Percents to Common Fractions

You know that percents are a form of fraction with an unwritten denominator of 100. A % sign is used.

To change any percent to a decimal, common fraction, or mixed number, divide by 100 and remove the percent sign.

To change a percent to a common fraction:

  • Write the numerals in the percent as the numerator.
  • Write 100 as the denominator. (Remember that the line in a fraction can be a divided by sign, so [latex]58\%=\tfrac{58}{100}[/latex] is the same as [latex]58\div100[/latex].)
  • Remove the % sign.
  • Simplify the fraction: [latex]\tfrac{58}{100}=\tfrac{29}{50}[/latex]

Example A

Write each percent as a common fraction.

[latex]38\%=\dfrac{38}{100}\div\left(\dfrac{2}{2}\right)= \dfrac{38 \div 2}{100 \div 2} =\dfrac{19}{50}[/latex]

[latex]25\%=\dfrac{25}{100}\div\left(\dfrac{25}{25}\right)= \dfrac{25\div 25 }{100 \div 25}=\dfrac{1}{4}[/latex]

[latex]3\%=\dfrac{3}{100}[/latex]

Note that percents greater than or equal to 100 become improper fractions which will be rewritten as mixed numbers.

Here is an example:

[latex]110\%=\dfrac{110}{100}=1\dfrac{10}{100}=1\dfrac{1}{10}[/latex]

[latex]\begin{array}{r}1\\ 100\enclose{longdiv}{110}\\\underline{100}\\ 10\end{array}[/latex]

Here is another example:

[latex]120\%=\dfrac{120}{100}=1\dfrac{20}{100}=1\dfrac{1}{5}[/latex]

[latex]\begin{array}{r}1\\ 100\enclose{longdiv}{120}\\ \underline{100}\\ 20\end{array}[/latex]

Remember 100% is the whole thing: [latex]100\%=1[/latex].

Exercise 8

Change each percent to a common fraction. Simplify to lowest terms.

  1. [latex]31\%=[/latex]
  2. [latex]11\%=[/latex]
  3. [latex]2\%=[/latex]
  4. [latex]20\%=[/latex]
  5. [latex]75\%=[/latex]
  6. [latex]100\%=[/latex]
  7. [latex]750\%=[/latex]

Answers to Exercise 8

  1. [latex]\tfrac{31}{100}[/latex]
  2. [latex]\tfrac{11}{100}[/latex]
  3. [latex]\tfrac{1}{50}[/latex]
  4. [latex]\tfrac{1}{5}[/latex]
  5. [latex]\tfrac{3}{4}[/latex]
  6. [latex]1[/latex]
  7. [latex]7\tfrac{1}{2}[/latex]

Percents Less Than 1%

Sometimes a percent smaller than 1% is used. For example, you will hear amounts such as [latex]\tfrac{1}{4}\%[/latex] or [latex]\tfrac{1}{8}\%[/latex] or [latex]\tfrac{1}{2}\%[/latex] on the news about the Bank of Canada rate and the rise and fall of inflation. These are small amounts. Sometimes the expression “[latex]\tfrac{1}{2}\text{ of a percentage point}[/latex]” is used instead of “[latex]\tfrac{1}{2}\%[/latex]”.

What is [latex]\tfrac{1}{4}\%[/latex]?

[latex]\tfrac{1}{4}\%[/latex] is [latex]\tfrac{1}{4}\text{ of }1\%[/latex]

[latex]1\%=\tfrac{1}{100}[/latex], so [latex]\tfrac{1}{4}\text{ of }1\%=\tfrac{1}{4}\times\tfrac{1}{100}=\tfrac{1}{400}[/latex]

[latex]\tfrac{1}{4}\%=0.25\%=0.0025[/latex]

What is [latex]\tfrac{1}{2}\%[/latex]?

[latex]\tfrac{1}{2}\%=\tfrac{1}{2}\text{ of }1\%=\tfrac{1}{2}\times\tfrac{1}{100}=\tfrac{1}{200}[/latex]

[latex]\tfrac{1}{2}\%=0.5\%=0.005[/latex]

To work with percents less than 1%, change the percent to a decimal by dividing by 100 (move decimal point two places to the left).

[latex]0.2\%=0.002[/latex]

[latex]0.75\%=0.0075[/latex]

If the percent is expressed as a common fraction, do this:

  • Write the common fraction percent as a decimal percent.
  • Divide by 100 (move decimal point two places left).

[latex]\begin{array}{rcrcl} \tfrac{1}{2}\% &= &0.5\% &=& 0.005 \\ \tfrac{1}{4}\% &= &0.0025\% &=& 0.0025 \\ \tfrac{1}{8}\% &=& 0.00125\% \ & =& 0.00125 \end{array}[/latex]

Exercise 9

Change each percent to an equivalent decimal.

  1. [latex]\tfrac{1}{2}\%=[/latex]
  2. [latex]0.6\%=[/latex]
  3. [latex]\tfrac{3}{10}\%=[/latex]
  4. [latex]\tfrac{3}{5}\%=[/latex]
  5. [latex]0.75\%=[/latex]
  6. [latex]\tfrac{3}{4}\%=[/latex]
  7. [latex]0.5\%=[/latex]
  8. [latex]\tfrac{1}{4}\%=[/latex]
  9. [latex]0.125\%=[/latex]
  10. [latex]\tfrac{5}{8}\%=[/latex]

Answers to Exercise 9

  1. [latex]0.005[/latex]
  2. [latex]0.006[/latex]
  3. [latex]0.003[/latex]
  4. [latex]0.006[/latex]
  5. [latex]0.0075[/latex]
  6. [latex]0.0075[/latex]
  7. [latex]0.005[/latex]
  8. [latex]0.0025[/latex]
  9. [latex]0.00125[/latex]
  10. [latex]0.00625[/latex]

16⅔%, 33⅓%, 66⅔%, 83⅓% …

These percents will become repeating decimals. For example:

[latex]\begin{equation}\begin{split} 33\tfrac{1}{3}\% &= 33.\overline{3}\% &= 0.33\overline{3} \\ \\ 66\tfrac{2}{3}\% &= 66.\overline{6}\% &= 0.66\overline{6} \end{split}\end{equation}[/latex]

It is usually more convenient to use the common fraction equivalent of these percents. Memorize them, or make a note on a special paper and post it near your work space.

[latex]\begin{equation}\begin{split} 33\tfrac{1}{3}\% &= 33\tfrac{1}{3}\div100 &= \tfrac{100}{3}\times\tfrac{1}{100} \ &= \tfrac{1}{3} \\ \\ 66\tfrac{2}{3}\% &= 66\tfrac{2}{3}\div100 &= \tfrac{200}{3}\times\tfrac{1}{100} \ &= \tfrac{2}{3} \end{split}\end{equation}[/latex]

[latex]\begin{equation}\begin{split} 16\tfrac{2}{3}\% &= \tfrac{1}{6} \\ \\ 33\tfrac{1}{3}\% &= \tfrac{1}{3} \\ \\ 66\tfrac{2}{3}\% &= \tfrac{2}{3} \\ \\ 83\tfrac{1}{3}\% &= \tfrac{5}{6} \end{split}\end{equation}[/latex]

Review of Equivalent Common Fractions, Decimals, and Percents

Complete this chart. These are equivalents that you will often use, so use this chart for reference. Memorize as many equivalents as you can. You may wish to put other equivalents on the chart.

Common Fraction Decimal Percent
[latex]\tfrac{1}{4}[/latex]
[latex]0.5[/latex]
[latex]75\%[/latex]
[latex]\tfrac{1}{8}[/latex]
[latex]0.375[/latex]
[latex]62.5\%[/latex]

Answers to Review of Equivalent Common Fractions, Decimals, and Percents

Common Fraction Decimal Percent
[latex]\tfrac{1}{4}[/latex] [latex]0.25[/latex] [latex]25\%[/latex]
[latex]\tfrac{1}{2}[/latex] [latex]0.5[/latex] [latex]50\%[/latex]
[latex]\tfrac{3}{4}[/latex] [latex]0.75[/latex] [latex]75\%[/latex]
[latex]\tfrac{1}{8}[/latex] [latex]0.125[/latex] [latex]12.5\%[/latex]
[latex]\tfrac{3}{8}[/latex] [latex]0.375[/latex] [latex]37.5\%[/latex]
[latex]\tfrac{5}{8}[/latex] [latex]0.625[/latex] [latex]62.5\%[/latex]

Topic A: Self-Test

Mark       /15                  Aim        13/15

  1. Write these percents in numeral form. (2 marks)
    1. Sixty-two and one-half percent
    2. One hundred six and one-fifth percent
  2. Write these percents in words. (2 marks)
    1. [latex]72\%[/latex]
    2. [latex]\tfrac{3}{4}\%[/latex]
  3. Change the percents to decimal fractions. (5 marks)
    1. [latex]32\%[/latex]
    2. [latex]18.5\%[/latex]
    3. [latex]125\%[/latex]
    4. [latex]\tfrac{4}{5}\%[/latex]
    5. [latex]\tfrac{2}{3}\%[/latex]
  4. Change these percents to common fractions in lowest terms. (4 marks)
    1. [latex]16\%[/latex]
    2. [latex]20\%[/latex]
    3. [latex]106\%[/latex]
    4. [latex]75\%[/latex]
  5. Change these common fractions to equivalent percents. (2 marks)
    1. [latex]\tfrac{4}{5}[/latex]
    2. [latex]\tfrac{3}{8}[/latex]

Answers to Topic A Self-Test

    1. [latex]62.5\%[/latex] or [latex]62\tfrac{1}{2}\%[/latex]
    2. [latex]106.2\%[/latex] or [latex]106\tfrac{1}{5}\%[/latex]
    1. Seventy-two percent
    2. Three-quarters percent
    1. [latex]0.32[/latex]
    2. [latex]0.185[/latex]
    3. [latex]1.25[/latex]
    4. [latex]0.008[/latex]
    5. [latex]0.00\overline{6}[/latex]
    1. [latex]\tfrac{4}{25}[/latex]
    2. [latex]\tfrac{1}{5}[/latex]
    3. [latex]1\tfrac{3}{50}[/latex]
    4. [latex]\tfrac{3}{4}[/latex]
    1. [latex]80\%[/latex]
    2. [latex]37.5\%[/latex]

License

Icon for the Creative Commons Attribution 4.0 International License

Adult Literacy Fundamental Mathematics: Book 6 - 2nd Edition Copyright © 2022 by Liz Girard and Wendy Tagami is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book