Perimeter and Area
12 Area
Click play on the following audio player to listen along as you read this section.

John is a painter who is going to paint a wall in a house. What he needs to know is how much paint he needs to buy for this one particular wall. He knows that the wall is in the shape of a rectangle and that the dimensions are 10 feet high by 27 feet wide.
How do you think he would go about solving this problem?
The answer lies in finding the area of the wall. A can of paint will be able to cover a certain area and if John can find out the area of the wall then he can figure out how many cans of paint he will need.
The first thing we should do here is write down the definition of area.
Area: The amount of space inside the boundary of a flat (2-dimensional) object such as a triangle, square, or circle.
The following are some two dimensional shapes shaded in grey. The grey portion represents the area of the object while the black lines surrounding the object represent the perimeter.

Area of a Square or Rectangle
Before we begin going through the motions to calculate the area of a square or rectangle lets take a quick visit back to perimeter and more specifically how we defined the dimensions of both a square and a rectangle.
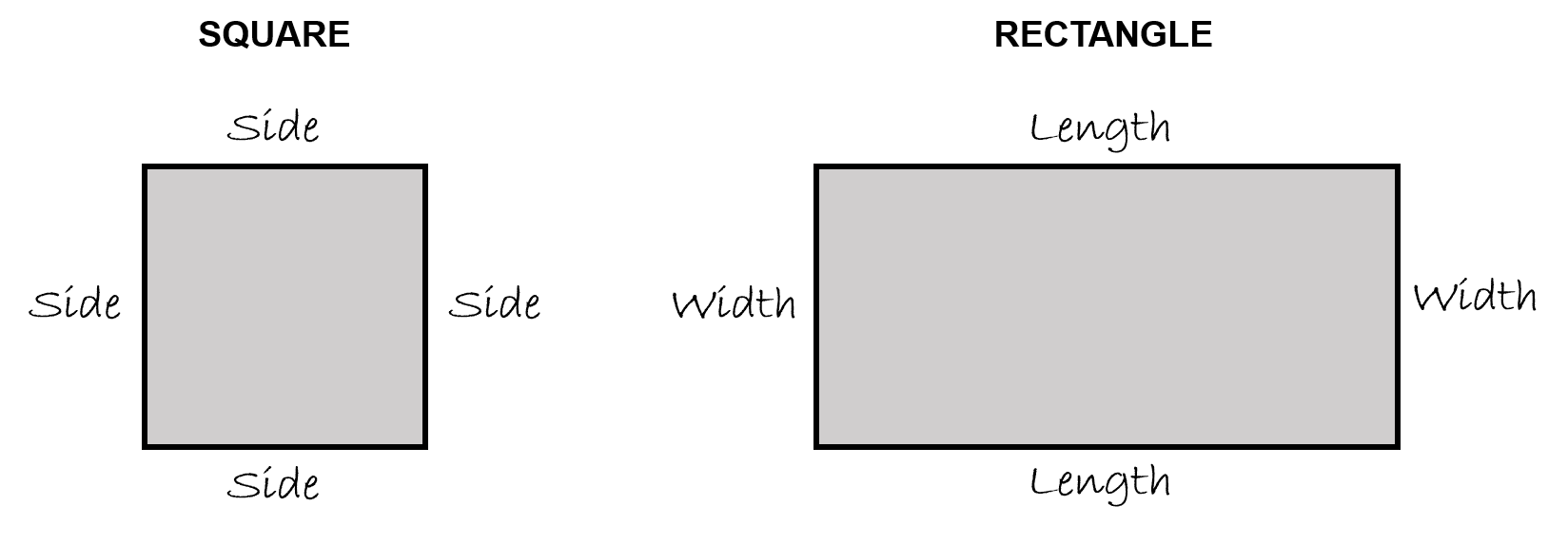
Once again the portion shaded grey is the area of each of the object. The question becomes this…

Can we use those dimensions when calculating the area? Or do we need to somehow come up with other dimensions in order to get to our answer?
Well as it turns out, those dimensions will work for us. Not only do they come in handy when we are calculating perimeter, but they also work really well when calculating area.

The next question then becomes HOW do we use these dimensions?
Before you move on to see how it’s done, take a minute to think about it. Maybe even write down some of your thoughts. Once again, this goes back to something we talked about before. If you are able to understand the concept then the process involves less memorization.

Here are the formulas for calculating the area of both a square and a rectangle.
[latex]\Large \begin{array}{ll}\textbf{Square:} & \text{Area} = \text{side} \times \text{side}\\ \textbf{Rectangle:}&\text{Area}= \text{length}\times \text{width}\end{array}[/latex]

Take note here as there are a couple things different than dealing with perimeter. The first is that we are now multiplying rather than adding. This ends up leading to our second point.
If we take a look at the formula for the square we see that we multiply a side by a side. As all the sides are the same it doesn’t really matter which two sides we multiply together.
The issue becomes the units that we end up with. Remember that when dealing with perimeter we are only dealing with a one dimensional line. Our units end up being linear or essentially one dimensional.
With area we end up with units that give us an answer using two dimensional units. The best way to understand this is to go through an example.
Let’s say we have a square where each side is 5 inches long.

Using the formula for area of a square we would get…
[latex]\Large \begin{array}{c} \text{Area} = \text{side} \times \text{side} \\ \text{Area} = 5 \text{ inches} \times 5 \text{ inches}\end{array}[/latex]
We can conclude that 5 times 5 is equal to 25 but what happens when we multiply inches times inches.
[latex]\Large \text{inches} \times \text{inches} = ?[/latex]
Well inches times inches ends up being inches squared or if you were to write it down it would look like this:
[latex]\Large {\text{inches}}^{2} \qquad \text{OR}\qquad {\text{in}}^{2}[/latex]
So when you see measurements, such as feet, inches, miles, kilometres and so on with the square symbol after them what you are dealing with is a measurement of area. Put another way it is a measurement stated in two dimensions.
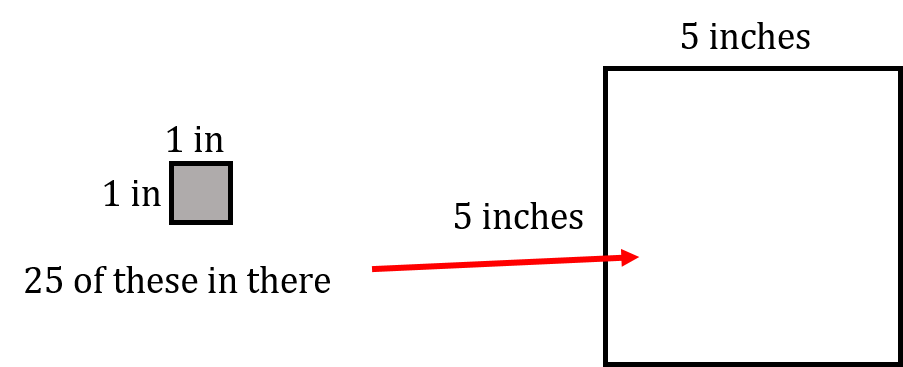
If we go back to our example we would end up with this:
[latex]\Large \begin{array}{c} \text{Area} = \text{side} \times \text{side} \\ \text{Area} = 5 \text{ inches} \times 5 \text{ inches} \\ \text{Area} = 25 {\text{ in}}^{2} \end{array}[/latex]
If we were to look at it visually here is what we would have:
Example
Calculate the area of a square where a side is 14 cm..
Step 1: Write down the formula.
[latex]\Large \text{Area} = \text{side} \times \text{side}[/latex]
Step 2: Solve for area.
[latex]\Large \begin{array}{c} \text{Area} = \text{side} \times \text{side} \\ \text{Area} = 14 \text{ cm} \times 14 \text{ cm} \\ \text{Area} = 196 {\text{ cm}}^{2}\end{array}[/latex]
Example
A rectangle has a length of 22 inches and a width of 15 inches. Calculate the area of the rectangle.
Step 1: Write down the formula.
[latex]\Large \text{Area} = \text{length} \times \text{width}[/latex]
Step 2: Solve for area.
[latex]\Large \begin{array}{c} \text{Area} = \text{length} \times \text{width} \\ \text{Area} = 22 \text{ in} \times 15 \text{ in} \\ \text{Area} = 330 {\text{ in}}^{2} \end{array}[/latex]

Let’s say that we wanted to get the answer into feet squared (ft²). How do you think you would go about that? The best way to look at that is visually. The first thing that we have to remember is that:
[latex]\Large \text{foot} = 12 \text{ inches}[/latex]
Remember that’s a linear or one dimensional measurement. What we are looking to end up with is a two dimensional measurement.
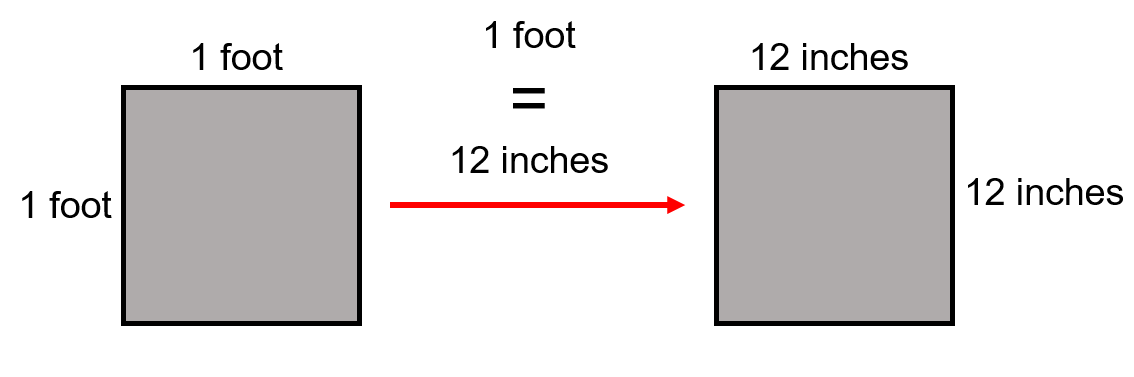
[latex]\Large \begin{array}{cc} \text{Area} = \text{side} \times \text{side} & \text{Area} = \text{side} \times \text{side} \\ \text{Area} = 1 \text{ ft} \times 1 \text{ ft} & \text{Area} = 12 \text{ in} \times 12 \text{ in} \\ \text{Area} = 1 {\text{ ft}}^{2} & \text{Area} = 144 {\text{ in}}^{2}\end{array}[/latex]
[latex]\Large \text{therefore} \longrightarrow 1 {\text{ ft}}^{2} = 144 {\text{ in}}^{2}[/latex]
Basically it takes 144 square inches to make one square foot.
Example
A square has a side of 15 inches. What is the area of the square in square feet?
Step 1: Write down the formula.
[latex]\Large \text{Area} = \text{side} \times \text{side}[/latex]
Step 2: Solve for area.
[latex]\Large \begin{array}{cc} \text{Area} = \text{side} \times \text{side} \\ \text{Area} =15 \text{ in} \times 15\text{ in} \\ \text{Area} = 225 {\text{ in}}^{2} \end{array}[/latex]
Step 3: Convert inches squared to feet squared.
[latex]\Large \begin{array}{ccl}1{\text{ ft}}^{2}=144{\text{ in}}^{2} & & \\ \text{therefore} & \longrightarrow & {\text{ft}}^{2} = \dfrac{{\text{in}}^{2}}{144 {\text{/ft}}^{2}}\\ & & {\text{ft}}^{2} = \dfrac{225 {\text{ in}}^{2}}{144 {\text{ in/ft}}^{2}} \\ & & {\text{ft}}^{2} = 1.56 {\text{ ft}}^{2} \end{array}[/latex]
Area of a Triangle

Although a triangle has straight lines similar to a square or a rectangle it differs in the fact that it has three sides and not four. This means that the previous equations using side, length or width will not work in this example. Consider the following picture of a triangle. What we have to work with in our equation is known as the “base” and the “height.”
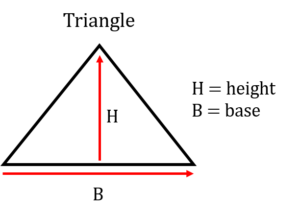
As it turns out triangles are not always in the configuration shown above. It doesn’t matter though as you could turn the triangle any which way and eventually get to a point where there is a “base” and a “height.”
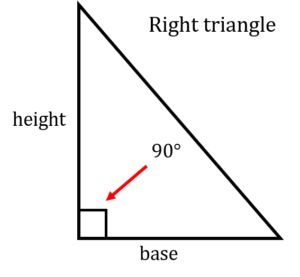
Another version of a triangle is the one pictured to the left. This version is the one that helps us derive our formula for area of a triangle. What we have to the left is what is known as a “right” triangle. A right triangle is defined as any triangle that has one angle of 90°. It also has the characteristics of a triangle in that it has a base and a height along with three sides. Now take that triangle and make another one exactly like it but reverse its position like the picture below.
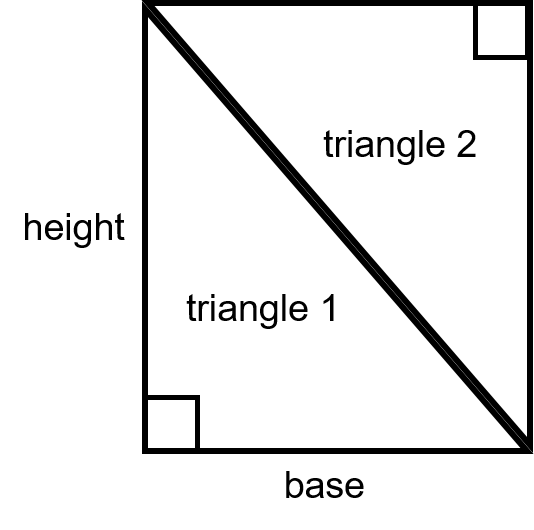
What’ll you note from the above drawing is that when you put the two triangles together they make a rectangle. They could also make a square if the base and the height were the same.
In any case when we look back at the formula for a rectangle is was length multiplied by width. In this case if we multiplied the base time the height we would end up with the area of both triangles.
So it make sense then that the area of one of the triangle would be the area of the base multiplied by the height and then take that answer and divide it into two equal parts.
And in the end that’s exactly what the formula for a triangle is. Note that this works for any triangle even if it’s not a right triangle. The main goal is to get the correct base measurement and the correct height measurement.
Formula:
[latex]\Large \text{Area} = \dfrac{\text{base} \times \text{height}}{2}[/latex]
Let’s go through as example.
Example
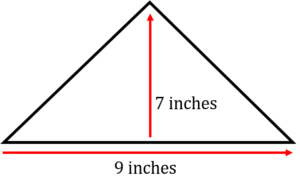
Find the area of a triangle given that it’s base is 9 inches and it’s height is 7 inches?
Step 1: Write down the formula.
[latex]\Large \text{Area} = \dfrac{\text{base} \times \text{height}}{2}[/latex]
Step 2: Solve for area.
[latex]\Large \begin{array}{c} \text{Area} = \dfrac{9 \text{ inches} \times 7 \text{ inches}}{2} \\ \text{Area} = \dfrac{63 {\text{ in}}^{2}}{2} \\ \text{Area} = {31.5 \text{ in}}^{2} \end{array}[/latex]
Examples
Find the area of a triangle given that it’s base is 12 inches and it’s height is 10 inches?
Step 1: Write down the formula.
[latex]\Large \text{Area} = \dfrac{\text{base} \times \text{height}}{2}[/latex]
Step 2: Solve for area.
[latex]\Large \begin{array}{c} \text{Area} = \dfrac{12 \text{ inches} \times 10 \text{ inches}}{2} \\ \text{Area} = \dfrac{120 {\text{ in}}^{2}}{2} \\ \text{Area} = 60 {\text{ in}}^{2} \end{array}[/latex]
We’ll try one more example but this time we’ll switch it up a bit and the area and base will be given and we’ll have to solve for height.
Example
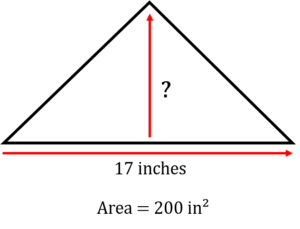
Find the height of a triangle whose base is 17 inches and whose area is 200 in².
Step 1: Write down the formula.
[latex]\Large \text{Area} = \dfrac{\text{base} \times \text{height}}{2}[/latex]
Step 2: Rearrange the formula so solve for height.
[latex]\Large \text{Height} = \dfrac{\text{Area} \times 2}{\text{base}}[/latex]
Step 3: Solve for height.
[latex]\Large \begin{array}{c} \text{Height} = \dfrac{\text{Area} \times 2}{\text{base}} \\ \text{Height} = \dfrac{200 {\text{ in}}^{2} \times 2}{17 \text{ in}} \\ \text{Height} = 23.53 \text{ in}\end{array}[/latex]

Take a look at the units the final answer is in. Note that they are in inches but in the question the area is in inches squared.
It does make sense that the height is in inches as it’s a linear measurement and one dimensional but how do we arrive at that answer? Is there a mathematical explanation for it?
The answer is yes. Here is how it works.
What we need to start with is the units in the equation we are working with. We don’t worry about the actual values just the units.
[latex]\large \begin{array}{ccc}\text{Height}=\dfrac{{\text{area in inches}}^{2}}{\text{base in inches}} & & \\ \downarrow & & \\ \text{Height}= \dfrac{{\text{in}}^{2}}{\text{in}} & \longrightarrow & \text{Height} = \dfrac{ \text{in} \times \text{in}}{\text{in}} \\ & & \downarrow \\ & & \text{Now what we do is cancel out} \\ & & \text{any units that are the same}\\ & & \downarrow \\ & & \text{Height}=\dfrac{ \text{in}\times \cancel{\text{in}}}{\cancel{\text{in}}} \\ & & \downarrow \\ & & \text{Height} = \text{inches} \\ & & \text{And we are left with inches}\end{array}[/latex]
Practice Questions
Try a couple practice questions for yourself. Make sure to check the video answers to see how you did.
Question 1

We’ll go back to John the painter for this one. John has to paint a wall with dimensions of 22 feet in length by 9 feet in width. The width is really the height of the wall in this case. Calculate the area in both square feet and square inches.
Question 2

We’ll stick with John the painter for the second question. He has been asked to put a new coat of paint on a barn. He has calculated the area of most of the barn using the formula for a rectangle but the upper portion of the barn forms a triangle shape. Calculate the area to be painted in the triangle portion of the barn keeping in mind that there is one triangle on one end of the barn and another triangle on the other end of the barn.. The triangle portion has a base of 37 feet and a height of 9 feet.
Area of a Circle

If you remember back in the perimeter portion of this chapter we looked at the perimeter (circumference) of a circle. To get that calculation we had to know one of two characteristics of the circle. Finding the area of a circle follows a similar path. Once again height, width or length will not work for us as there are no straight lines on a circle. What we need to work with is either the radius or the diameter.
Interestingly there are two different ways to find the area of a circle. One includes using the radius and one includes using the diameter. Both equations work equally well but generally when dealing with the trades we use the formula which uses diameter.

Remember at some point back in another chapter I talked about the idea that learning to understand concepts can help to eliminate the need to memorize formulas. Well this fun fact can help your conceptual understanding of the area for a circle.
The first step in the process is to take a circle and fit it perfectly into a square.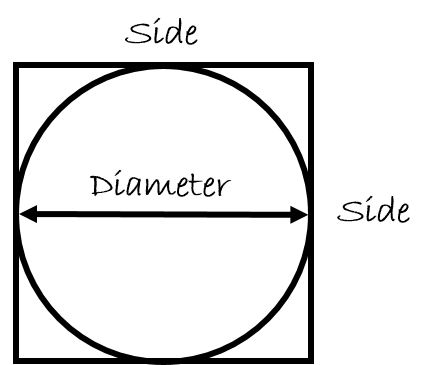
What you will notice is that the side of the square is the same length as the diameter of the circle.
[latex]\Large \text{DIAMETRE} = \text{SIDE}[/latex]
Here’s the fun fact!
As it turns out the area of a circle that is put perfectly inside a square takes up exactly 78.54 percent of the area of the square.
This information is how we can derive the formula for area of a circle.
If the formula for area of a square is side × side then if we took 78.54 percent of that answer we would get the area of the circle.
Now as we can see that the diameter is the same length as the side then we can say going diameter × diameter would get us the area of the square and then taking 78.54 percent of this would also get us the area of the circle.
Lucky for us the diameter is one of the characteristics of a circle that we would use.
So after that long winded explanation what we end up with is this:
[latex]\Large \begin{array}{c} \textbf{Area of a circle} \\ \text{Area} = \text{diameter} \times \text{diameter} \times 0.7854 \\ \text{OR } \\ \text{Area} = {\text{d}}^{2} \times 0.7854 \end{array}[/latex]
In this formula the 0.7854 represents the 78.54 percent that we were talking about earlier.
You may be looking at this equation thinking you remember another equation for the area of a circle and in this case your memory would be correct. The formula above is the one we use for trades but if you were to use the formula below you would also be correct.
[latex]\Large \begin{array}{c} \text{Area} = \pi \times {\text{radius}}^{2} \\ \text{OR} \\ \text{Area} = \pi {\text{r}}^{2} \end{array}[/latex]
In this case π is a constant.. As stated before this formula is also correct but generally when doing trades math we’ll stick to the formula using diameter.
Example
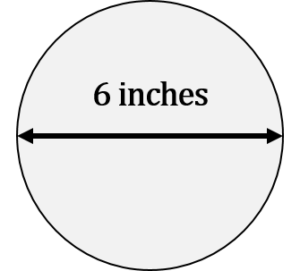
What is the area of a circle if the diameter is 6 inches?
Step 1: Write down the formula.
[latex]\Large \begin{array}{c} \text{Area} = {\text{d}}^{2} \times 0.7854 \\ \text{where: diameter} = 6 \text{ inches} \\ \text{constant} = 0.7854 \end{array}[/latex]
Step 2: Input variables and solve for area.
[latex]\Large \begin{array}{c} \text{Area} = {\text{d}}^{2} \times 0.7854 \\ \text{Area} = {6}^{2} \times 0.7854 \\ \text{Area} = 6 \text{ in} \times 6 \text{ in} \times 0.7854 \\ \text{Area} = 28.27 {\text{ in}}^{2} \end{array}[/latex]
Remember that as we are finding the area of a two dimensional object our answer ends up being squared. Once again inches squared represents two dimensions. Before we go on to another example let’s try the same question but this time we’ll use the other formula for area.
Step 1: Write down the formula.
[latex]\Large \begin{array}{c} \text{Area} = \pi {\text{r}}^{2} \\ \text{where: diameter} = 6 \text{ inches} \\ \text{radius} = 3 \text{ inches} \\ \text{constant} = 3.14 \end{array}[/latex]
Step 2: Input variables and solve for area.
[latex]\Large \begin{array}{c} \text{Area} = \pi {\text{r}}^{2} \\ \text{Area} = \pi \times {3}^{2} \\ \text{Area} = 3.14 \times 3 \text{ in} \times 3 \text{ in}\\ \text{Area} = 28.26 {\text{ in}}^{2} \end{array}[/latex]
As you can see either formula generates the same answer. Although any questions we go through will use the formula with diameter feel free to use the formula with radius. In the end all that matters is the you understand the process and you get the correct answer
Example
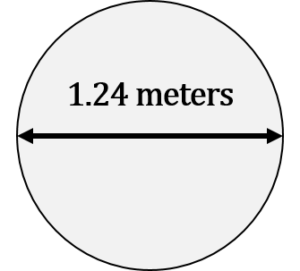 What is the area of a circle given that the diameter of the circle is 1.24 metres?
What is the area of a circle given that the diameter of the circle is 1.24 metres?Step 1: Write down the formula.
[latex]\Large \begin{array}{c} \text{Area} = {\text{d}}^{2} \times 0.7854 \\ \text{where: diameter} = 1.24 \text{ metres} \\ \text{constant} = 0.7854 \end{array}[/latex]
Step 2: Input variables and solve for area.
[latex]\Large \begin{array}{c} \text{Area} = {\text{d}}^{2} \times 0.7854 \\ \text{Area} = {1.24}^{2} \times 0.7854 \\ \text{Area} = 1.24 \text{ m} \times 1.24 \text{ m} \times 0.7854 \\ \text{Area} = 1.208 {\text{m}}^{2} \end{array}[/latex]
Practice Question
Try a practice question for yourself. Make sure to check the video answer to see how you did.
Exercises

Jascarn is installing 6 inch pot lights in the ceiling of a friend’s house. What is the area of the hole that Jascarn will have to cut out in order to fit in a 6 inch diameter pot light?

