Volume
16 Volume of a Sphere
Click play on the following audio player to listen along as you read this section.
 To the left we have a picture of our beautiful planet, Earth. Although the picture itself is two dimensional, we know that Earth is three dimensional. This implies that Earth has a volume. What is also true is that Earth is an example of a sphere.
To the left we have a picture of our beautiful planet, Earth. Although the picture itself is two dimensional, we know that Earth is three dimensional. This implies that Earth has a volume. What is also true is that Earth is an example of a sphere.

So far we’ve calculated the volume of cubes, rectangular tanks, and cylinders. Using that information, how do you think we would calculate the volume of a sphere? What variables do you think you would use? Take a few moments to think about it before we go through the explanation below.
Just in case you were wondering, Earth has a volume of…
[latex]\Large 1,083,206,916,846 \text{ cubic kilometres}[/latex]
There are two things to note here:
- The answer is once again in cubic units.
- That’s a lot of volume.


We should start this explanation off by revisiting the formula for a circle. Remember that a circle had a radius, diameter, and circumference. Also remember that to find the formula for a circle, we could have used one of two formulas.
[latex]\Large \begin{array}{ll} \text{Formula one:} & \text{ area} = {\text{d}}^{2} \times 0.7854 \times \text{h} \\ \text{Formula two:} & \text{ area} = \pi {\text{r}}^{2} \end{array}[/latex]
When dealing with the formula for a sphere, we can use formula two as a starting point. The formula for a sphere has a similar feel to it but with a little twist. The similarities include having both pi and radius in the formula, but that is where the similarities end.
Here is the formula:
[latex]\Large \text{volume} = \dfrac{4}{3} \pi {\text{r}}^{3}[/latex]
The question becomes, “Where does the 4/3 come from?” Well the explanation for that is actually quite a long one, and I’ll leave that for another day. Quickly stated, it comes from the fact that if you took two cones with similar measurements to the sphere, it would end up that the volume of those two cones would equal the volume of the sphere. Using a bit of mathematical wizardry the 4/3 ends up being derived from this fact.

The pi in the formula is the constant that we use when finding the circumference of a circle, and the radius, as you might remember, is half the length of the diameter. The last thing is that the radius is cubed. This relates to the fact that in the end we are solving for volume, which has three dimensions.
Now I didn’t expect you to get the formula as it’s quite a bizarre one, but understanding where it comes from helps to conceptualize the formula. As we talked about previously, the purpose of this exercise is to rely less on memorization and more on an understanding of how stuff is derived.
Example

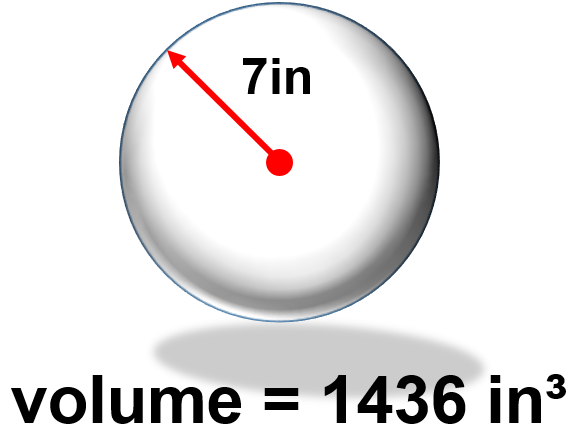
Find the volume of a sphere with a radius of 7 inches.
Step 1: As usual write down the formula.
[latex]\Large \text{volume} = \dfrac{4}{3} \pi {\text{r}}^{3}[/latex]
Step 2: Plug in the variables and solve for volume
[latex]\Large \begin{array}{c}\text{volume} = \dfrac{4}{3} \pi {\text{r}}^{3} \\ \text{volume} = \dfrac{4}{3} \pi {7}^{3} \\ \text{volume} = \dfrac{4}{3} \times \pi \times 7 \times 7 \times 7 \\ \text{volume}= 1436{\text{ in}}^{3} \end{array}[/latex]
Examples
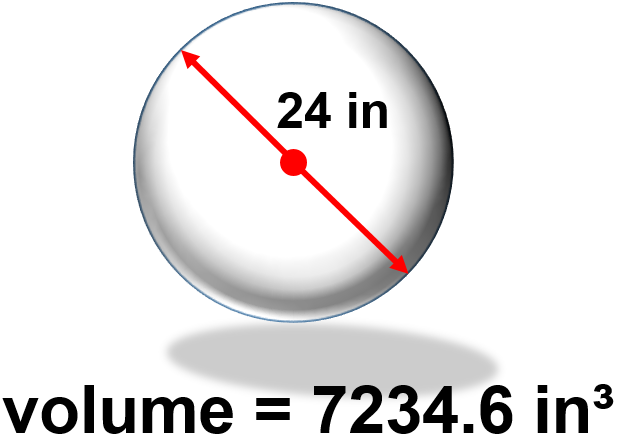
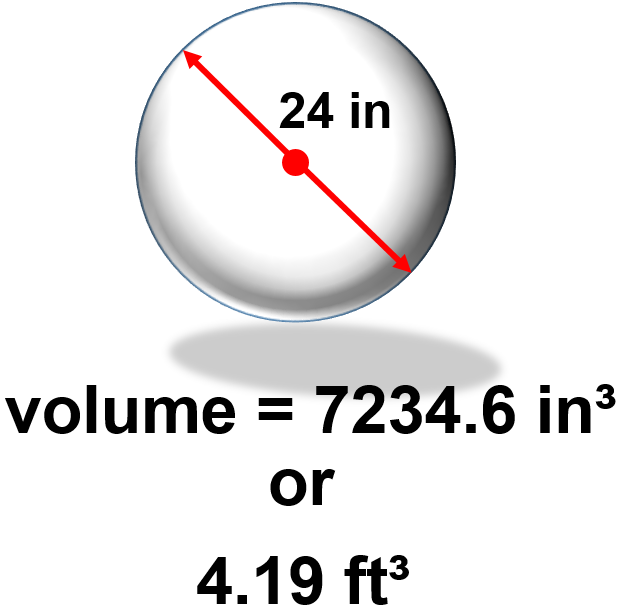
Let’s take a step up here and add a little twist. Find the volume of a sphere with a diameter of 24. Note that the diameter will go through the exact center of the sphere. Think of where you are standing right now, and drill a hole straight down through the Earth to the exact other side making sure to go through the dead centre of the Earth. (Disclaimer: I think there is an Arnold Schwarzenegger movie plot somewhere inside this question.) Anyway, back to the question.
Step 1: As usual, write down the formula.
[latex]\Large \text{volume} = \dfrac{4}{3} \pi {\text{r}}^{3}[/latex]
I’m going to guess that by this time in the book, you’ve started to see some patterns and have picked out the fact that we need to use the radius in the formula but we only have diameter. We’ll have to work a little math magic, and pull the radius out of the diameter before we start.
[latex]\Large \begin{array}{c}\text{diameter} = \text{radius} \times 2 \\ \text{radius} = \dfrac{\text{diameter}}{2} \\ \text{radius} = \dfrac{24}{2} \\ \text{radius} = 12 \end{array}[/latex]
Now we have what we need to work with.
Step 2: Plug in the variables and solve for volume.
[latex]\Large\begin{array}{c} \text{volume} = \dfrac{4}{3} \pi {\text{r}}^{3} \\ \text{volume} = \dfrac{4}{3} \pi {12}^{3} \\ \text{volume} = \dfrac{4}{3} \times \pi \times 12 \times 12 \times 12 \\ \text{volume}= 7234.6 {\text{ in}}^{3} \end{array}[/latex]

Hey! Should we throw in a bonus question here? Okay, let’s do it. Change the volume from cubic inches into cubic feet.
Step 1: Write down the formula.
[latex]\Large 1 \text{ cubic foot} = 1728 \text{ cubic inches}[/latex]
Step 2: Cross multiply
[latex]\Large \begin{array}{c}\dfrac{1 {\text{ ft}}^{3}}{{\text{X ft}}^{3}} = \dfrac{1728 {\text{ in}}^{3}}{7234.6 {\text{ in}}^{3}} \\ 1 \times 7234.6 = \text{X} \times 1728 \\ \text{X} = \dfrac{7234.6}{1728} \\ \text{X} = 4.19{\text{ ft}}^{3} \end{array}[/latex]
Practice Question
Try a practice question yourself and check the video answer to see how you did.
Question 1

Josh and Jatinder are both fans of the NBA and in class they are discussing what the volume of a basketball might be. They’ve figured out that the diameter of a basketball is 9.5 inches. Calculate the volume of the basketball.

