Volume
15 Volume of a Cylinder
Click play on the following audio player to listen along as you read this section.

What do you think is in the tank in the picture to the left?
Maybe water? Maybe grain? Maybe old math textbooks for the construction trades?

For us right now, it’s less important to know what is in the tank and more important to know how to figure out how much stuff can fit into the tank.
This type of tank in known as a cylinder and is comprised of three basic parts. It has a top, a bottom, and a middle section. We will assume that the top and the bottom are both perfect circles with equal diameter and equal area.

A good example of a cylinder would be a hot water tank. Take a look at the hot water tank to the right and ask yourself what you might need to know if you were required to calculate the volume of the tank.
What did you come up with? How about trying your hand at coming up with a formula. I’ll give you one hint before you give it a shot.
Hint: Volume is in cubic form. For example: cubic feet, cubic metres, cubic inches, etc.

Formula for Volume of a Cylinder
Here’s the formula.
[latex]\Large \text{volume of cylinder} = {\text{diameter}}^{2} \times 0.7854 \times \text{height}[/latex]

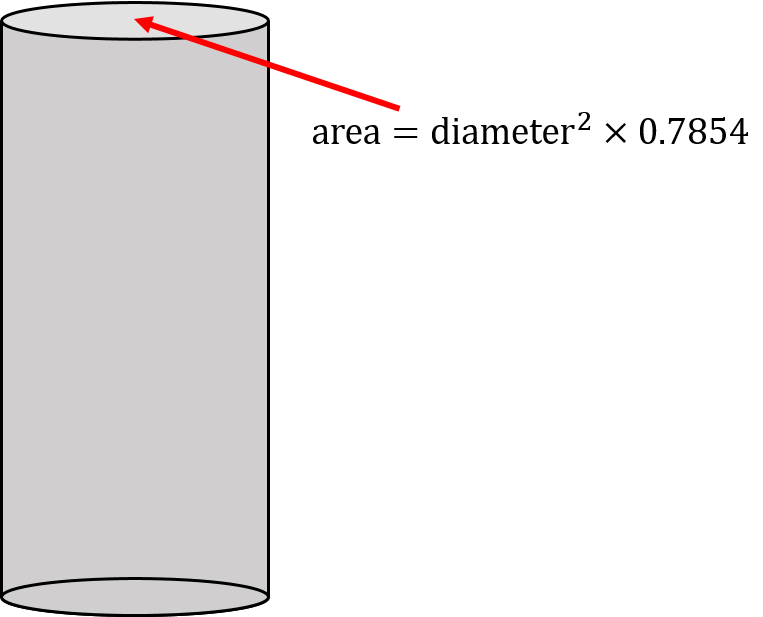
Remember that the top of a cylinder is simply a circle. It has a diameter, a radius, and a circumference. The bottom of the tank has the same dimensions as the top of the tank.
So we need this calculation (the area of the top or bottom) to use as a starting point.
The next question that would come about is, “How high or how long is the tank?”
This would also play a big part in calculating the volume.
Put this all together and you get your formula:
[latex]\Large \text{volume of cylinder} = {\text{diameter}}^{2} \times 0.7854 \times \text{height}[/latex]
One last question:

What kind and type of units will we be dealing with in our answer?
Units for Volume of a Cylinder
There are actually two parts to this answer.
Part 1
The answer remains in whatever units the variables are that we are dealing with. So for instance, if we are dealing with feet then our answer would end up being some version of feet. If we are dealing with inches then our answer would end up being some version of inches.

Note that you have two different variables here, diameter and height. Make sure that when working out your answer that both variables are in the same units. If diameter is in inches and height is in feet, you would have to convert one or the other so that they would both be the same unit.
Part 2
As stated earlier, our answer would be in cubic units. Although we have only two variables (diameter and height), the diameter is squared therefore we could write the formula like the following:
[latex]\Large \text{volume} = \text{diameter} \times \text{diameter} \times 0.7854 \times \text{height}[/latex]
In the end, we would actually have three variables with two of them being the same. This is how we get our answer in cubic (3) units.
Examples
A cylindrical tank has a diameter of 7 inches and a height of 51 inches. What is the volume of the tank?
Step 1: write down the formula and identify the variables.
[latex]\Large \begin{array}{c} \text{volume of a cylinder} = {\text{diameter}}^{2} \times 0.7854 \times \text{height}\\ \textbf{Variables} \\ \text{height (h)} = 51 \text{ inches} \\ \text{diameter (d)} = 7 \text{ inches} \end{array}[/latex]

Now before we move on, check and make sure the variables are in similar units. If they are different, we’ll have to change them so they are both the same.
Lucky for us, in this question they are both in inches so we are good to go.
Step 2: Plug the variables into the formula, and work through the question.
[latex]\Large \begin{array}{c} \text{volume} ={\text{d}}^{2} \times 0.7854 \times \text{h} \\ \text{volume}= 7 \text{ in} \times 7 \text{ in} \times 0.7854 \times 51 \text{ in} \\ \text{volume} = 1962.7 {\text{ in}}^{3}\end{array}[/latex]
Example
Calculate the volume of a cylindrical tank that has a diameter of 555 millimetres and a height of 7.9 metres.
Step 1: Write down the formula and identify the variables.
[latex]\Large \begin{array}{c} \text{volume of a cylinder} = {\text{diameter}}^{2} \times 0.7854 \times \text{height}\\ \textbf{Variables} \\ \text{height (h)} = 555 \text{ millimetres} \\ \text{diameter (d)} = 7.9 \text{ metres} \end{array}[/latex]

The two variables are in different units. We have to change one or the other to put both in the same units. In this case, we will work with metres and our answer will then end up in metres cubed.

The height being 7.9 metres works for us but the diameter being 555 millimetres does not. We will have to change that to metres in order for everything to be consistent.
We will have to go back a few chapters and into our memory bank for this one.
Remember that 1 metre = 1000 millimetres.
To get the number of metres in 555 millimetres we do the following:
[latex]\Large \begin{array}{c} 1 \text{ metre} = 1000 \text{ millimetres} \\ \text{metres} = \dfrac{\text{number of millimetres}}{1000 \text{ millimetres/metre}} \\ \text{metres} = 0.555 \text{ metres} \end{array}[/latex]
Now that both of the variables are in similar units we can go ahead and solve for volume.
Step 2: Plug the variables into the formula and work through the question.
[latex]\Large \begin{array}{c} \text{volume} = {\text{d}}^{2} \times 0.7854 \times \text{h} \\ \text{volume} = 0.555 \text{ m} \times 0.555 \text{ m} \times 0.7854 \times 7.9 \text{ m} \\ \text{volume} = 1.91 {\text{ m}}^{3}\end{array}[/latex]
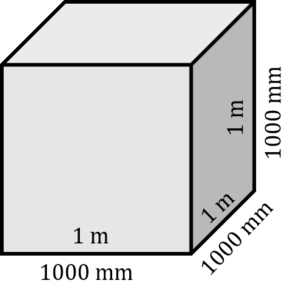
So we have our answer in cubic metres but what if wanted to change that answer to cubic millimetres? We’ll go back to our drawing of a cube to find out the relationship between cubic metres and cubic millimetres.
[latex]\Large \begin{array}{lc}\text{In metres:} & \text{volume} = \text{ side}\times \text{side} \times \text{side} \\ & \text{volume} = 1 \text{ m} \times 1 \text{ m} \times 1 \text{ m} \\ & \text{volume} = 1 {\text{ m}}^{3} \\ \text{In millimetres:} & \text{volume} = \text{ side} \times \text{side} \times \text{side} \\ & \text{volume} = 10 \text{ mm} \times 10 \text{ mm} \times 10 \text{ mm} \\ & \text{volume} = 1,000,000,000{\text{ mm}}^{3} \end{array}[/latex]
So in the end one cubic metre equals a lot of cubic millimetres More precisely one cubic metre equals one billion cubic millimetres.
So how many cubic millimetres are there in our cylindrical tank in the example above.
[latex]\Large \begin{array}{c} {\text{ mm}}^{3} = {\text{ mm}}^{3} \times 1,000,000,000 {\text{ mm}}^{3}{\text{/m}}^{3} \\ {\text{ mm}}^{3} = {1.91}^{3} \times 1,000,000,000 {\text{ mm}}^{3}{\text{/m}}^{3} \\{\text{ mm}}^{3} = 1,910,000,000 \end{array}[/latex]
Practice Questions
Try a couple practice questions for yourself. Make sure to check the video answers to see how you did.
Question 1

Gerrard is going to be installing a new hot water tank. The tank is 1 foot three inches in diameter and 5 feet 2 inches in height. What is the volume of the tank in cubic feet?
Question 2

A one gallon paint can is approximately 6 ½ inches in diameter and 7 ½ inches in height. One gallon is enough to paint up to 400 square feet which works out to be about the area of a small bathroom.
Calculate the volume of the paint can in both cubic inches and cubic feet.

