Volume
14 Volume of a Cube or Rectangular Tank
Click play on the following audio player to listen along as you read this section
 If you were asked to describe the volume of an object, what would that look like? How would you describe the units your calculation would be in?
If you were asked to describe the volume of an object, what would that look like? How would you describe the units your calculation would be in?
This chapter deals with the calculation of volume and the units used when calculating volume.
In the last chapter we dealt with perimeter, which is a linear measurement. As we found out, perimeter is one dimensional and essentially takes on the characteristics of a line. A good example of perimeter would be if you walked around the outside of a soccer field. You would have walked the perimeter of the field.
Then we took a look at area, which is a two-dimensional measurement. A good example of that is a table top. If you were to take a paint brush and repaint the top of the table, you would be painting the area of the table top.

When dealing with volume, we are adding one more dimension, and this ends up making volume a three-dimensional measurement. A good example of a three dimensional object would be the planet Earth.

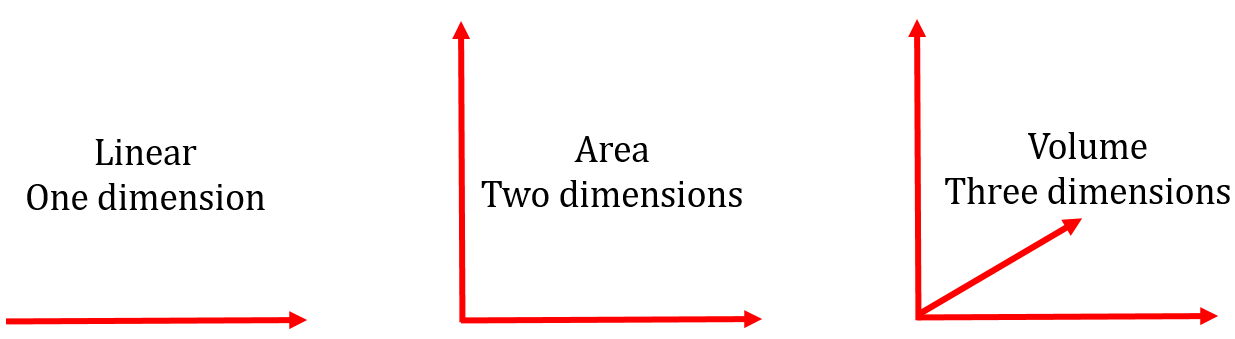
Here is another visual representation of each of the three. Each line represents a plane.
Now let’s revisit units. When we deal with a linear measurements, we deal with units as they are. By that I mean we would get the answer in metres, feet, inches, centimetres and so on.
When we deal with area, we keep dealing with units such as metres, but they are squared to indicate that they have two dimensions. For instance, an apartment might have an area of 1200 feet squared or 1200 ft². The squaring of the feet indicates two dimensions, such as a width AND length.
But now we add one more dimension into the mix. Not only might we have a length and a width, but we might also have a depth. This leads us to ask, “What would the units be in this situation?“
Well if we had metres as our unit then the answer would be metres cubed. If we were to write it similar to how we wrote down area, it would look like this:
[latex]\Large{\text{metre}}^{3} \qquad \text{or} \qquad {\text{m}}^{3}[/latex]
The “3” in this case represents three dimensions and is responsible for the term “cubed” when we sound it out. Now we are ready to go on and find out the formula for the volume of specific objects.
Volume of a Cube
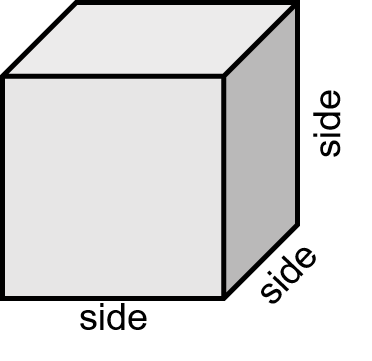
When the word “cube” is stated, we can think of a square but just with another dimension added. Each dimension on a square is identical and a cube follows that same logic.
If you add a third dimension, you get all possible dimensions being the same. Take a look at one of the most famous cubes in the world:

In order to find the volume of the cube, we need to multiply three sides together. More specifically, we would look at multiplying the length, the width, and the height. Because all three sides are the same, the formula ends up looking like the following:
[latex]\Large \text{volume of a cube} = \text{side} \times \text{side} \times \text{side}[/latex]
To find the area of a cube is pretty straight forward. All you have to know is the length of one side, and you have all the information you need.
Example
Find the volume of a cube where one side is 7 inches.
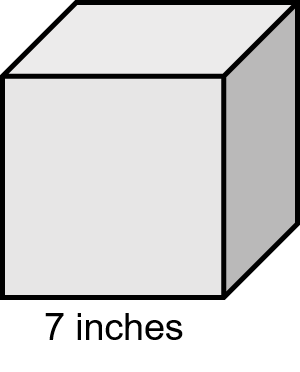
Step 1: Write down the formula.
[latex]\Large \text{volume of a cube} = \text{side} \times \text{side} \times \text{side}[/latex]
Step 2: Solve for volume.
As all the sides of a cube are the same, it means that each side is 7 inches.
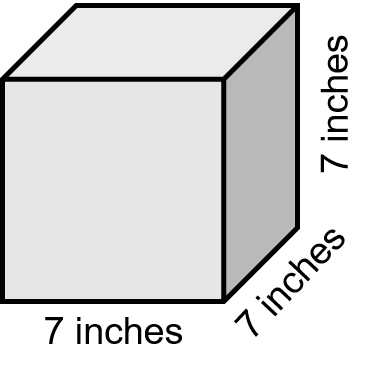
So when putting the variables into the equation they are all equal.
[latex]\Large \begin{array}{c} \text{volume of a cube} = \text{side} \times \text{side} \times \text{side} \\ \text{volume} = 7 \text{ in} \times 7 \text{ in} \times 7 \text{ in} \\ \text{volume} = 343 {\text{ in}}^{3} \end{array}[/latex]
Volume of a Rectangular Tank
How to calculate the volume of a rectangular tank is very similar to how to calculate the volume of a cube except for the fact that the dimensions of a rectangular tank will all be different. From this point on, we’ll just refer to it as a tank.
What we also get is that the names of the variables in the tank are different. When we dealt with a rectangle, we referred to the variables as length and width.
Now we are just adding another variable that we will call “height.”
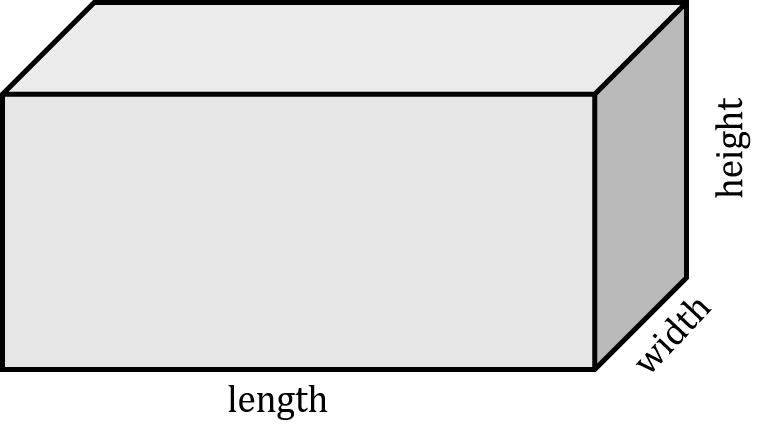
Once again, we are working with three dimensions, and the formula is going to be similar to that of a cube just with the variable “side” replaced by the three different variables of a tank.
Formula:
[latex]\Large \text{volume of a tank} = \text{length} \times \text{width} \times \text{height}[/latex]
Example
Calculate the volume of a tank that has a length of 17 inches, a width of 12 inches, and a height of 13 inches.
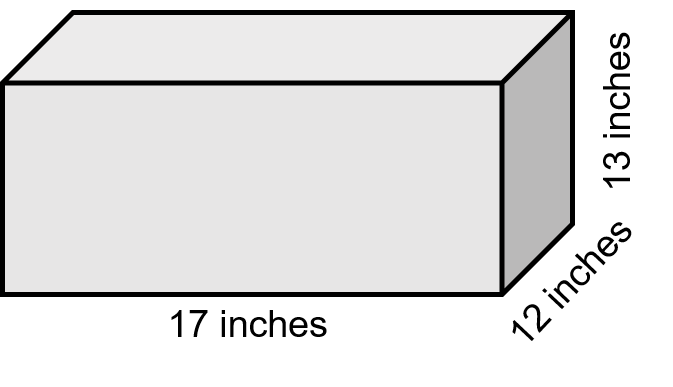
Step 1: Write down the formula.
[latex]\Large \text{volume of a tank} = \text{length} \times \text{width} \times \text{height}[/latex]
Step 2: Solve for volume.
[latex]\Large \begin{array}{c}\text{volume of a tank} = \text{length} \times \text{width} \times \text{height} \\ \text{volume} = 17 \text{ in} \times 13 \text{ in} \times 12 \text{ in} \\ \text{volume} = 2652 {\text{ in}}^{3} \end{array}[/latex]

Let’s put a twist on this now and put the answer into cubic feet.
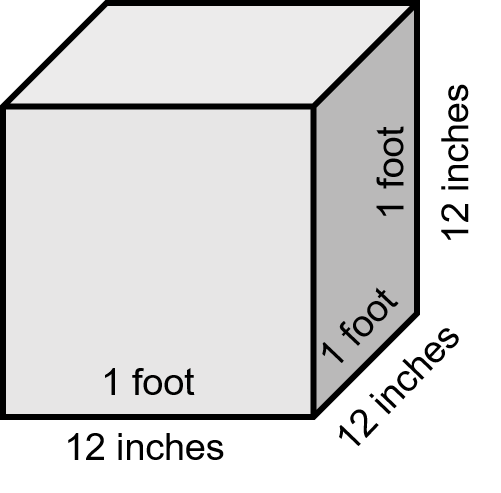
The first thing we have to do is calculate how many cubic inches there are in a cubic foot and the best way to do that is visually.
We would all agree that 1 foot equals 12 inches. Therefore using the formula for a cube we would get the following:
[latex]\Large \begin{array}{lc} \text{In feet:} & \text{volume} = \text{ side} \times \text{side} \times \text{side} \\ & \text{volume} = 1 \text{ ft} \times 1 \text{ ft} \times 1 \text{ ft} \\ & \text{volume} = 1{\text{ ft}}^{3} \\ \text{In inches:} & \text{volume} = \text{ side} \times \text{side} \times \text{side} \\ & \text{volume} = 12 \text{ in} \times 12 \text{ in} \times 12 \text{ in} \\ & \text{volume} = 1728 {\text{ in}}^{3} \end{array}[/latex]
So what we end with is:
[latex]\Large 1 {\text{ ft}}^{3} = 1728 {\text{ in}}^{3}[/latex]
Now we can answer the question.
How many cubic feet are there in a tank which contains 2652 cubic inches?
What you do here is take the number of cubic inches you have and divide it by the number of cubic inches there are in one cubic foot.
[latex]\Large\begin{array}{c} {\text{ ft}}^{3} = \dfrac{{\text{ in}}^{3}}{{\text{in}}^{3}{\text{/ft}}^{3}} \\ {\text{ ft}}^{3} = \dfrac{2652 {\text{ in}}^{3}}{1728 {\text{ in/ft}}^{3}} \\ {\text{ ft}}^{3}= 1.53 \end{array}[/latex]
Let’s go through another example and once again we’ll put a spin on the question.
Example
Find the width of a tank that has a length of 22 inches, a height of 14 inches and a total volume of 3080 cubic inches.
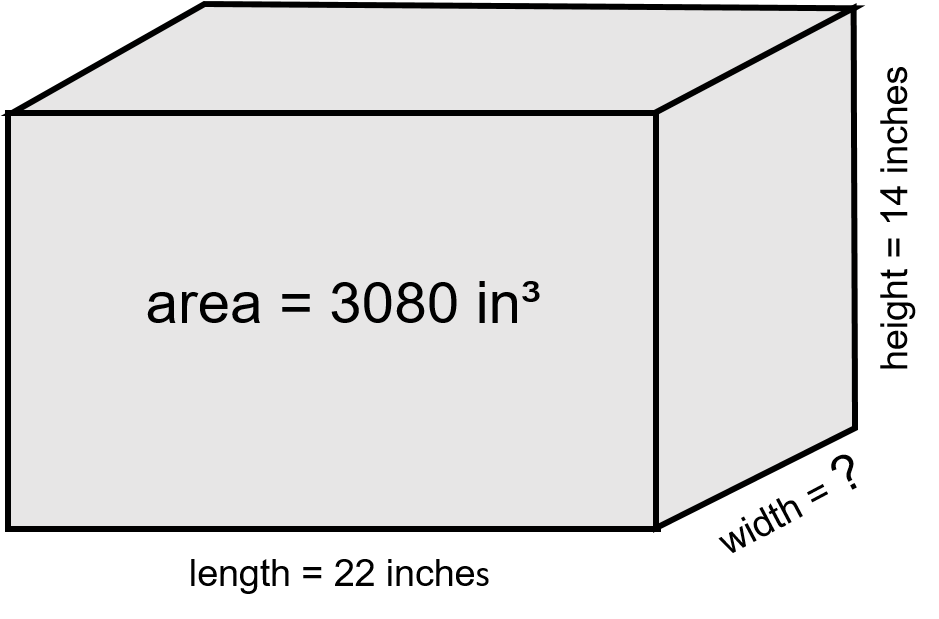
Step 1: Write down the formula.
[latex]\Large \text{volume} = \text{length} \times \text{width} \times \text{height}[/latex]
Step 2: Rearrange the formula to solve for width.
[latex]\Large \begin{array}{c} \text{volume} = \text{length} \times \text{width} \times \text{height} \\ \text{width} = \dfrac{\text{volume}}{\text{length} \times \text{height}} \end{array}[/latex]
Step 3: Calculate width.
[latex]\Large \begin{array}{c} \text{width} = \dfrac{\text{volume}}{\text{length} \times \text{height}} \\ \text{width} = \dfrac{3080 {\text{ in}}^{3}}{22 \text{ in} \times 14 \text{ in}} \\ \text{width} = 10 \text{ inches} \end{array}[/latex]
Practice Questions
Try a couple practice questions for yourself. Make sure to check the video answers to see how you did.
Question 1

Lyle works for a gas fitting company called “Night and Day Heating.” He’s designing a heating system for a building designed by an eccentric architect. The building is in the shape of a cube with one of the sides being 30 feet.
Lyle has to take into consideration the volume of the building before designing the system. What is the volume of the cubed building?
Question 2

Kate owns a septic tank installation company in rural British Columbia, and she has just hired Rachael who is originally from East Africa and has never installed a septic system before.
The tank is for a four-bedroom home and needs to have a total volume of at least 170 cubic feet according to the engineer who designed the system. The dimensions of the tank they are planning to install are down below. Given those dimensions, is the septic tank going to be large enough to meet the engineer’s demands.
Length = 7.5 feet
Width = 5.25 feet
Height = 4.5 feet

