Click play on the following audio player to listen along as you read this section.

In the last section we looked at the three ways grade is expressed and how to work between them. Now we need to put that to work in an equation which can give us the total fall of an object.

Take a look at the guy above. Any guesses on the grade he’s falling at?

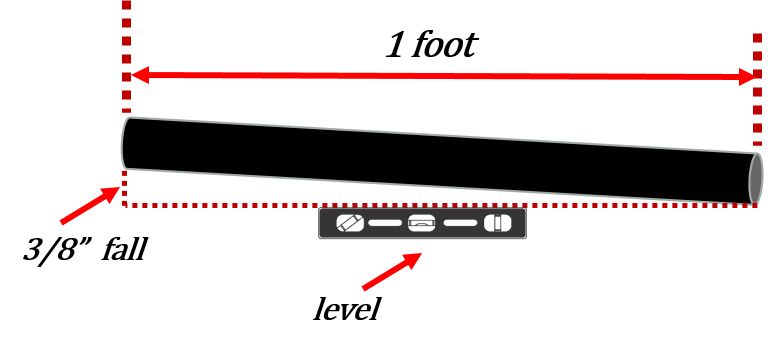
The first thing we do is look at what we are calculating and then figure out what variables we need. Let’s go back to this drawing from the last section.

If we start from the basics which is one foot and go from there we can build our formula.

I think we would all agree we need grade. In this particular case we can use a grade of inches per foot as we have a one foot piece of pipe falling three eighths of an inch. In our drawing we dealt with one foot but in reality we’ll more than likely be dealing with pipe that is longer than that. In the end it works out that we also need the length.

In conclusion we only require two variables.

1) Length
2) Grade

From this we can now build our formula.

[latex]\text{Total fall} = \text{length} \times \text{grade}[/latex]

It’s not actually the toughest formula to remember as there are only 3 variables if you include the answer. The trickiest part might just be dealing with the units as there are a few ways to express grade.

Usually we start off with the easiest example and then go to the harder ones but in this case we’ll start with the hardest.

Working With The Grade in Inches Per Foot

Expressing grade in inches per foot sets the formula up in a certain way.

Attention! The following is a very important point.

As the grade in this particular case is in inches per foot we MUST have the length in feet. 

Grade is expressed in inches per foot.

The length must be expressed in feet.

The total fall ends up being in inches.

Here’s how it works mathematically.

[latex]\text{Total fall (inches)} = \text{length (feet)} \times \text{grade (inches/foot)}[/latex]

or written another way…

[latex]\text{inches} = \text{feet} \times \text{inches/foot}[/latex]

The feet and the foot cancel each other out leaving just inches.

[latex]\begin{array}{c} \text{inches} = \cancel{feet} \times \dfrac{\text{inches}}{\cancel{foot}} \\ \text{inches } = \text{inches}\end{array}[/latex]

I know we’ve already talked about this but I want to bring up one point again. Note the total fall ends up in inches for this particular situation. This is key and very important.

Having said that let’s move on to another example involving grade in inches per foot. Maybe take a shot at doing this one yourself before moving on to the answer.

What is the total fall of a piece of pipe which travels 439 feet at a grade of 3/8 inches/ft?

Step 1:  Start with the formula.

[latex]\text{Total fall} = \text{length} \times \text{grade}[/latex]

Step 2:  Define your variables and make sure they are in the correct units.  

[latex]\text{Length} = 439 \text{ feet}[/latex]

[latex]\text{Grade} = \dfrac{3}{8} \text{ in/ft}[/latex]

Step 3:  Plug the variables into the formula.

[latex]\begin{equation}\begin{split} \text{Total fall} &= 439 \text{ feet} \times \dfrac{3}{8} \text{ inch/ft} \\ \text{Total fall} &= 439 \times \dfrac{3}{8} \end{split}\end{equation}[/latex]

Note: What you might think of doing at this point is to change the 3/8 into a decimal which might make it easier to work with.

[latex]3 \div 8 = 0.375[/latex]

You could then plug that into the formula.

[latex]\text{Total fall} = 439 \times 0.375[/latex]

Either way you end up with the same answer.

[latex]\text{Total fall} = 164.63 \text{ inches}[/latex]

Let’s step it up a notch and put the answer into eighths of an inch.

Step 4: Take the decimals of an inch and multiply it by 8. This turns the 0.63 inches into eighths of an inch.

[latex]0.63 \times 8 = 5.04[/latex]

In this case we round the 5.04 down to 5 and we end up with 5/8.

In the end our final answer becomes 164 5/8 inches.

Okay. Now that we have the hardest one out of the way it’s time to move onto the easier ones. Let’s start with the ratio.

Working With Grade as a Ratio

The reason a ratio is easier to work with as a grade is that it doesn’t come with any units. Why is this easier you ask? Well it works out that the total fall and the length are in the same units. There are no issues like there are when the grade is in inches per foot.

So for example if the length is in feet then the total fall is in feet. If the length is in miles then the total fall is in miles. It works out that when it comes to the grade being in a ratio things become much easier. Take a look at the following example.

A 175 foot length of sprinkler pipe needs to be run in a building at a grade of 1 in 200. What is the total fall of the sprinkler pipe?

Step 1:  Start with the formula.

[latex]\text{Total fall} = \text{length} \times \text{grade}[/latex]

Step 2:  Define your variables and make sure they are in the correct units.

[latex]\text{Length} = 175 \text{ feet}[/latex]

[latex]\text{Grade} = \dfrac{1}{200}[/latex]

Step 3:  Plug the variables into the formula.

[latex]\begin{equation}\begin{split} \text{Total fall} &= 175 \text{ feet} \times \dfrac{1}{200} \\ \text{Total fall} &= 0.875 \text{ feet} \end{split}\end{equation}[/latex]

Working With Grade as a Percent

Working with grade as a percent means the total fall ends up being in the same units that the length is expressed in. Once again this is due to the fact that when percentages are expressed in the total fall formula they come with no units.

There is one thing to remember though.

We’ll generally be given a percent expressed in a form like the figure below.

As we discussed in the previous section this format won’t work for us in the formula. It must be changed into decimal form in order for us to use it. This is done by taking the 2 and dividing it by 100.

Okay. So now that we have that out of the way let’s try an example.

Here’s another one. Try it on your own before looking at the answer down below.

A city drainage pipe runs through a neighborhood servicing the houses in the area. The drainage pipe runs a distance of 375 meters. It is required to be run at a grade of 1 percent. What is the total fall on the drainage pipe from beginning to end?

Step 1:  Start with the formula.

[latex]\text{Total fall} = \text{length} \times \text{grade}[/latex]

Step 2:  Define your variables and make sure they are in the correct units.

[latex]\text{Length} = 375 \text{ meters}[/latex]

[latex]\text{Grade} = 1\%[/latex]

Convert the grade into a workable form.

[latex]1 \div 100 = 0.01[/latex]

Step 3:  Plug the variables into the formula.

[latex]\begin{equation}\begin{split} \text{Total fall} &= 375 \text{ meters} \times 0.01 \\ \text{Total fall} &= 3.75 \text{ meters} \end{split}\end{equation}[/latex]

Try a few practice questions and check out the video answers to see how you did.

Practice Questions