Click play on the following audio player to listen along as you read this section.

Let’s start with what we know.

[latex]\begin{array}{c} 1 ft^3 &= 6.24 \text{ imperial gallons} \\ 1 ft^3 &= 7.48 \text{ U.S. gallons} \\ 1 \text{ imperial gallon} &= 1.2 \text{ U.S. gallons} \\ 1 m^3 &= 1000 \text{ litres} \end{array}[/latex]

Our goal in this chapter is to take all this information and figure out the relationship between gallons and litres. What we should calculate first is some type of common ground between the variables.

In the end the simplest way to express the common ground between the three might just be cubic feet. If we could calculate how many cubic feet are in an imperial gallon, a U.S. gallon as well as a litre then we could find the relationship between the three.

If you remember we already calculated the number of cubic feet in an imperial gallon as well as a U.S. gallon.

Here are those numbers once again.

[latex]1 \text{ imperial gallon} = 0.160 \text{ cubic feet}[/latex]

[latex]1 \text{ U.S. gallon} = 0.133 \text{ cubic feet}[/latex]

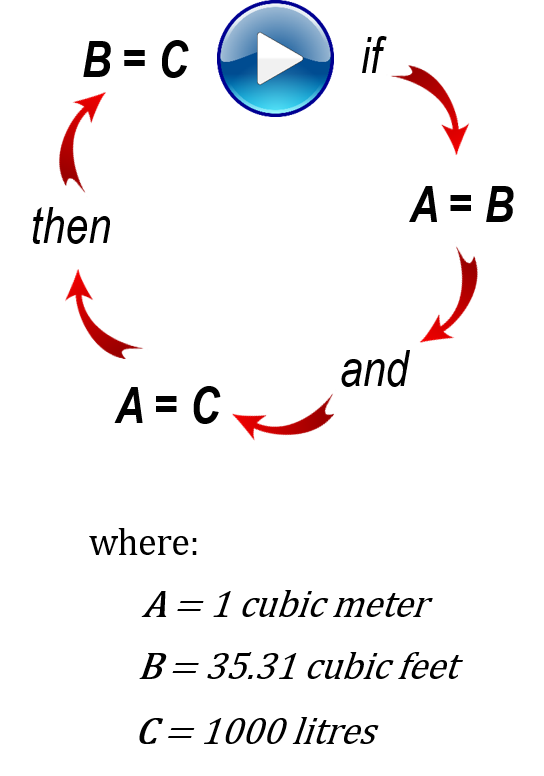
Let’s throw down some logic right about now to work through this. Remember back a few chapters ago we found out the following:

[latex]1 \text{ cubic meter} = 35.31 \text{ cubic feet}[/latex]

Now in this chapter we determined that:

[latex]1 \text{ cubic meter} = 1000 \text{ litres}[/latex]

Well then it makes sense that:

[latex]35.31 \text{ cubic feet} = 1000 \text{ litres}[/latex]

We can use this last nugget of information in order to calculate the number of cubic feet in one litre. We’ll cross multiply as that seems to come in handy for this type of stuff. First let’s take a look at a little visual which takes us through the logic we just went through.

Now back to cross multiplying in order to find the number of cubic feet in one litre.

[latex]\dfrac{35.31 \text{ cubic feet}}{\text{X cubic feet}} = \dfrac{1000 \text{ litres}}{1 \text{litre}}[/latex]

[latex]35.31 \times 1 = \text{X} \times 1000[/latex]

[latex]\begin{array}{c} \text{X} &= \dfrac{35.31}{1000} \\ \text{X} &= 0.0353 \text{ cubic feet}\end{array}[/latex]

[latex]\text{answer} = 0.0353 \text{ cubic feet}[/latex]

As you can see I’ve taken this to four decimal places. This is not something I usually do but as this is a small number being more exact will help us get a more exact answer in the end.

We can now write down each of the capacities in cubic feet.

[latex]\begin{array}{c} 1 \text{ imperial gallon} &= 0.160 \text{ cubic feet} \\ 1 \text{ U.S. gallon} &= 0.133 \text{ cubic feet} \\ 1 \text{ litre} &= 0.0353 \text{ cubic feet} \end{array}[/latex]

From those three pieces of information we should be able to calculate the relationship between litres and gallons. We’ll start with imperial gallons. Once again let’s do a little cross multiplying.

[latex]\dfrac{1 \text{ litre}}{\text{X litres}} = \dfrac{0.0353 \text{ cubic feet}}{0.160 \text{ cubic feet}}[/latex]

Remember that the 0.160 cubic feet in the above equation represents the number of cubic feet in an imperial gallon.

[latex]1 \times 0.160 = \text{X} \times 0.0353[/latex]

[latex]\begin{array}{c} \text{X} &= \dfrac{0.160}{0.0353} \\ \text{X} &= 4.54\end{array}[/latex]

[latex]\text{answer} = 4.54 \text{ litres}[/latex]

So in the end we get:

[latex]1 \text{ imperial gallon} = 4.54 \text{ litres}[/latex]

If you had gone through and done the math above you would find that it actually comes out to 4.53. No worries though. The reason its off by 0.01 is due to rounding earlier on in the process. For our purposes we’ll always go with 1 imperial gallon = 4.54 litres.

Next up is U.S. gallons. Do the same cross multiplying.

[latex]\dfrac{1 \text{ litre}}{\text{X litres}} = \dfrac{0.0353 \text{ cubic feet}}{0.133 \text{ cubic feet}}[/latex]

[latex]1 \times 0.133 = \text{X} \times 0.0353[/latex]

[latex]\begin{array}{c} \text{X} &= \dfrac{0.133}{0.0353} \\ \text{X} &= 3.78\end{array}[/latex]

[latex]\text{answer} = 3.78 \text{ litres}[/latex]

Once again going through the actual math would give us an answer of 3.77. We’re off by 0.01 due to rounding so in the end the number we always want to go with is 1 U.S. gallon = 3.78 litres.

So in the end we get that:

[latex]1 \text{ U.S. gallon} = 3.78 \text{ litres}[/latex]

Now we have the numbers we are looking for. Just for fun take 3.78 and add 20 percent to it. Remember that an imperial gallon is twenty percent larger than a U.S. gallon. You can do this mathematically by multiplying by 1.2.

[latex]3.78 \times 1.2 = 4.54[/latex]

It’s all working out and everyone is happy!

Here’s a quick summary.

We’re going to move on to some example in a second but I’d like to make a suggestion at this point. We’ve just gone through a fair bit of math and calculated a number of numbers.

You might want to go back to the start of this section and reread it before moving on. Maybe try taking some notes and summarizing what you just read through.

Try a couple practice questions yourself and check the video answers to see how you did.

Practice Questions