Pressure and Total Force
7 Using Water as a Guide for Determining Pressure
Click play on the following audio player to listen along as you read this section.

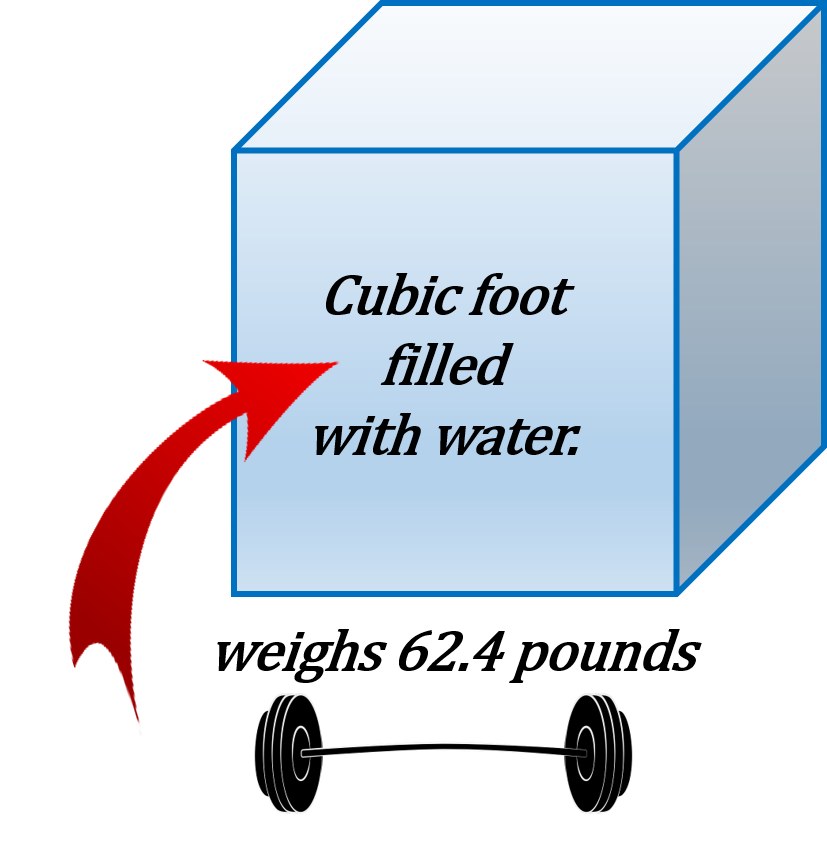
What does water have to do with determining pressure? Well all liquids including water have weight and that weight can translate into pressure. If I was to take one cubic foot of water and weigh it we would find that it weighs 62.4 pounds.
If I was to take that water and pour it into a container or into a pipe the weight of the water would exert a pressure onto the container or the pipe. The amount of pressure that it exerts depends on the height of the water. The higher the height of the water the greater the pressure exerted at the base of that container or pipe.

For example the water in the glass above exerts a pressure on all sides of the glass including the bottom. To calculate the pressure at the bottom of the glass we would need to find out the height of the water in the glass. It doesn’t matter what size the glass is only the height of it.
The Relationship Between Water, Height and Pressure
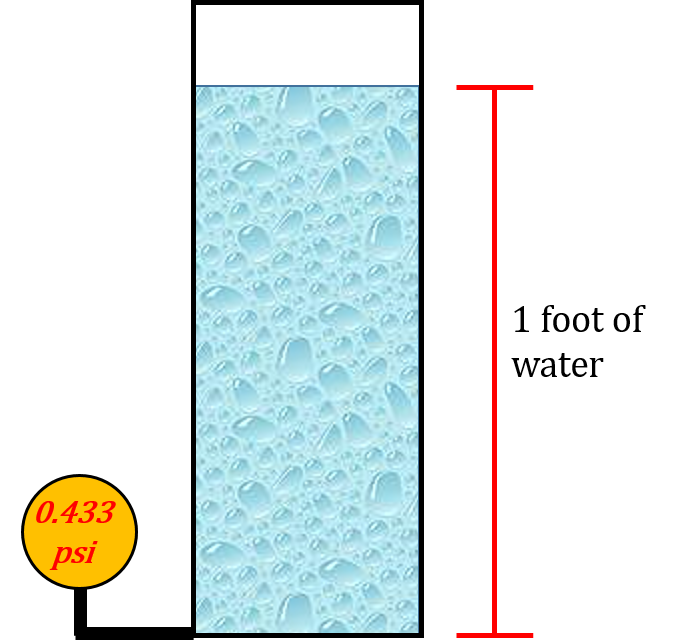
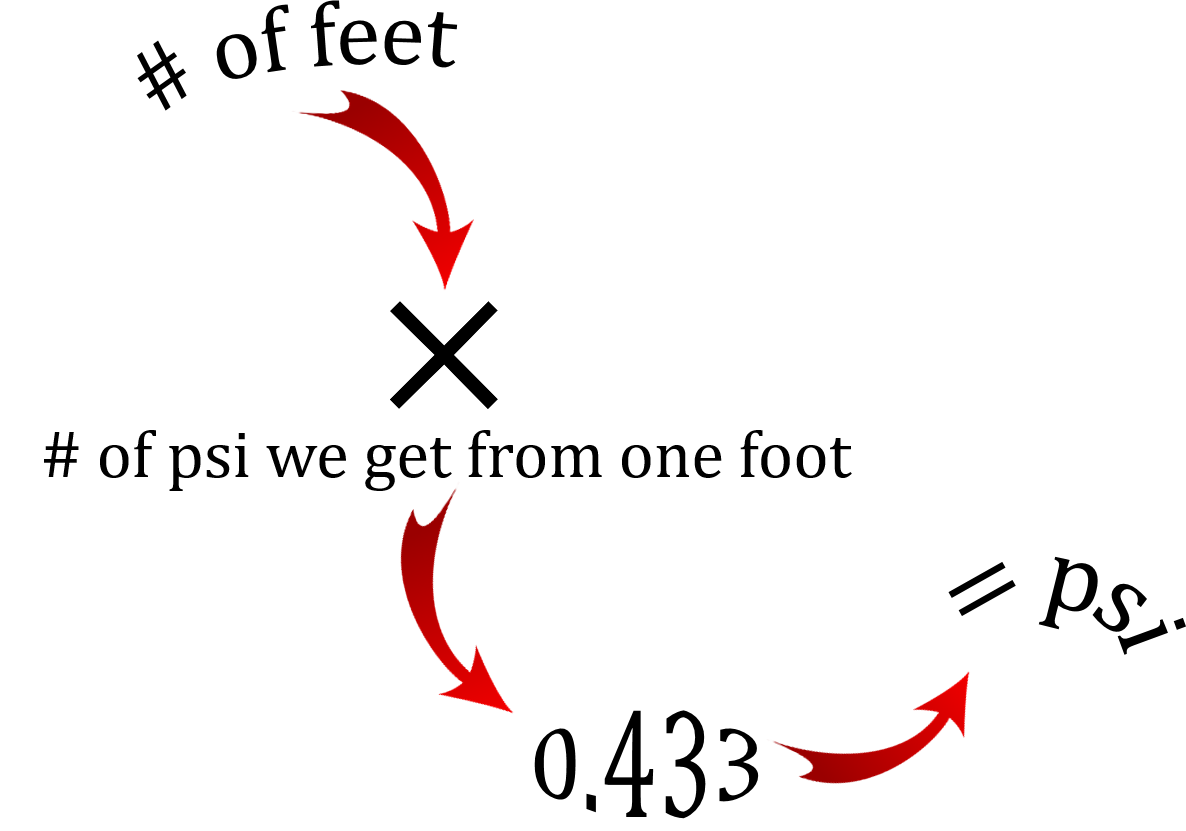
The relationship between water, height and pressure is constant. If we were to take a column of water 1 foot high and use a pressure gauge at the bottom to measure the pressure it would read 0.433 psi.
This is our constant when dealing with water and it remains consistent as we add more water. If we filled the column with more water that number on the pressure gauge would go up accordingly.

One thing I want to bring to your attention is the fact that we are measuring pressure. At this point we should remind ourselves that pressure is a force per unit area. In this case its pounds per square inch or psi. Regardless of the area at the bottom of the container we are only calculating the force on one square inch. Keep this in mind as later on in the chapter we’ll start to expand the concept and deal with the total area and eventually the total force.
As stated previously when we add more height in terms of water the relationship between the height and the pressure remains constant. What we would find is the following:
[latex]\text{PSI} = \text{ height in feet} \times 0.433[/latex]
What this relationship is saying is that for every foot we go up in height we add 0.433 pounds per square inch at the base of an object. Keep in mind that we are talking about water here and specifically the density and weight of water. Other liquids will have their own density and therefore the psi at the bottom of a column of another liquid would be different than that of water. I’ll go through an example of this in a bit but let’s just stick to water for now.
Example

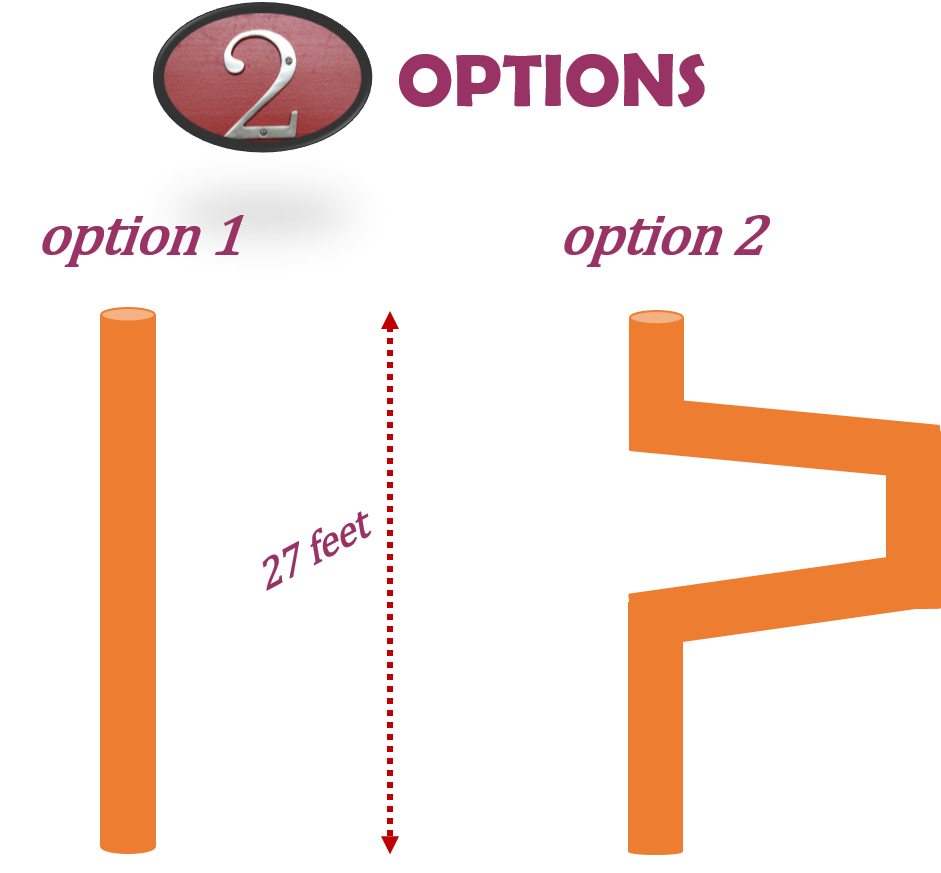
A piping system is filled with water. The piping system consists of pipe which extends through three floors of a building and has a total height of 27 feet. What would be the pressure exerted at the base of the piping system?

In order to answer the question we don’t actually need to know how the piping is configured. It doesn’t matter if the piping goes straight down or offsets at some point during it’s run. The only thing we need to know is how high the piping goes. This is the determinant when calculating pressure. Check out the drawing below to see what I mean.
Regardless of how the pipe is run the vertical distance from the beginning to the end is still 27 feet. This would be the number you would use to calculate the psi at the base of the pipe for each scenario. Now go through and check out how its done.
Step 1: As always identify what the question is asking. In this case we are looking to find the pressure at the base of a given piping system.
Step 2: Write down the formula you’ll be working with.
[latex]\text{PSI} = \text{ height in feet} \times 0.433[/latex]
Step 3: Cross multiply.
[latex]\dfrac{1 \text{ foot of height}}{27 \text{ feet of height}} = \dfrac{0.433 \text{ psi}}{\text{X psi}}[/latex]
[latex]\begin{array}{c} 1 \times \text{X} &= 27 \times 0.433 \\ \text{X} &= 27 \times 0.433 \\ \text{X} &= 11.69\end{array}[/latex]
[latex]\text{answer} = 11.69 \text{ psi}[/latex]
Therefore every inch of pipe at the bottom of the piping system experiences 11.69 pounds of pressure on it.
This type of relationship holds true for all liquids with the only difference being that the constant used will change when dealing with those different liquids.
If we were to add another liquid such as mercury we would have a totally different relationship. Let’s take a little detour and check it out.


The thermometer to the right has a bulb filled with mercury.
Mercury has a different density than water and therefore a different weight. One cubic foot of mercury weighs more than water. In fact it weighs a lot more. If we were to use mercury as our gauge to measure psi we would need to use the following relationship.
[latex]\text{PSI} = \text{ height in feet} \times 5.88[/latex]
What you can see from this is that mercury is indeed heavier than water and that filling a tube or pipe up with mercury one foot in height would end up giving you 5.88 psi at the base of that object.
Visually it would look like the diagram below. One cylinder is filled with mercury while the other is filled with water. Both are filled to a height of one foot. If we were to put a pressure gauge at the bottom of each one we would get different readings.

You can see that the pounds per square at the base of the cylinder is much greater for mercury than for water due to the fact that mercury has a greater density and weighs more.
Our detour is almost over. When dealing with piping systems we fill them up with water for testing purposes. We can fill the systems up to a particular height and then calculate how much pressure there is at the base of the system.
Water is a convenient liquid to use for testing purposes as its plentiful and easily available not to mention the fact that it’s not harmful although trying telling the boss that when you’ve flooded a suite with water. It seems pretty harmful then.
The question becomes “What is mercury used for?” Well if you’ve ever been in a hospital room you’ve most likely come across a situation where mercury is used when dealing with pressure.
Mercury is often used as a gauge when dealing with vacuums but not the kind that are used for cleaning up a room.
A vacuum occurs when we get to pressures below atmospheric pressure or 14.7 psia. Vacuum pumps intended to remove excess fluid from patients do this by creating a vacuum or suction. The pressure of this suction is measured in inches of mercury or you might see it written as “Hg” with Hg being the symbol for mercury.
As it turns out 2.04 inches of mercury is equal to 1 psi.

Alright. We’ve gone on a bit of a detour but let’s get back on track.
We came here to talk about water and how it translates into pounds per square inch.
We already calculated that having a column of water one foot in height gives us 0.433 psi at the base of that column.
Reminder: It doesn’t matter what the area is at the base of the column as the pressure is measure for each and every square inch. We’ll work the area into the equation later in the chapter.
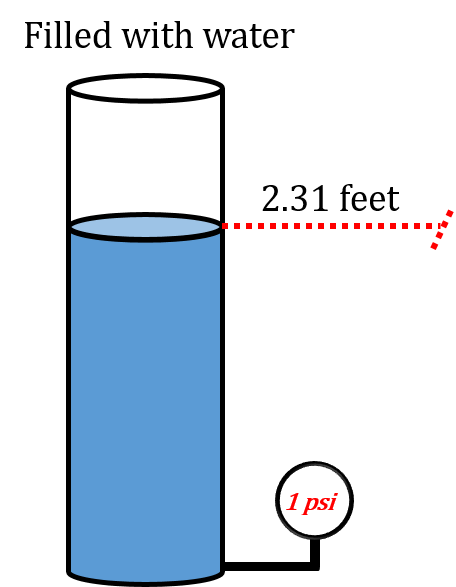
For now let’s concentrate on filling the column up with more water. How high do you think we would have to fill the column in order to get a pressure at the base of 1 psi?
Take a look at the following picture.
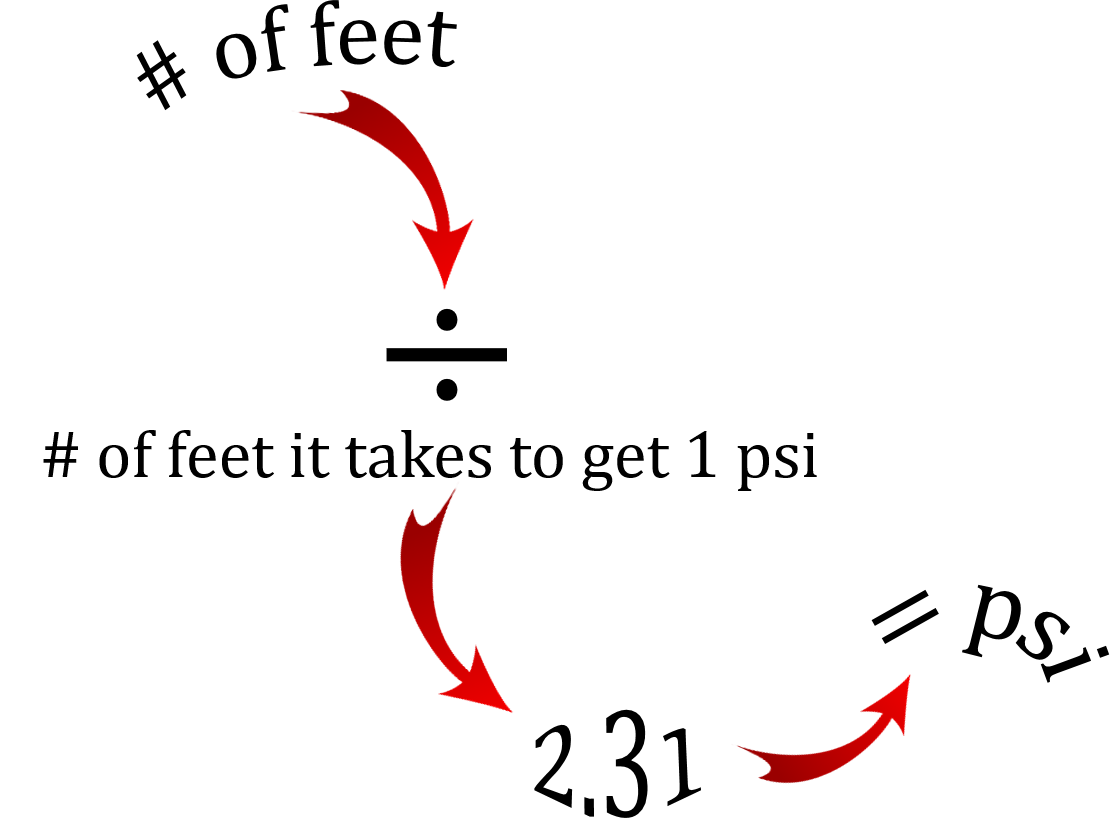
As you can see filling up the column of water to a height of 2.31 feet gives us a pressure at the base of 1 psi.
This is where things get interesting if you like math. There is a relationship between the numbers 0.433 and 2.31.
What we have are the numbers 1, 0.433 and 2.31. We’ll arrange them to form an equation.
[latex]\dfrac{1}{2.31} = 0.433[/latex]
OR…
[latex]\dfrac{1}{0.433} = 2.31[/latex]
OR…
[latex]2.31 \times 0.433 = 1[/latex]
The idea is that there is a definite relationship between the three numbers. Whichever way you look at it is up to you. Personally I go with the first version of the equation. In my head this is the easiest one to visualise.
So in summary we can say that when dealing with water we get:
[latex]1 \text{ ft} = 0.433 \text{ psi}[/latex]
[latex]2.31 \text{ ft} = 1 \text{ psi}[/latex]
Example
What we’ll do here is go through an example of calculating psi using both the number 0.433 and the number 2.31.
A column of water stands 17.78 feet high. What is the pressure at the base of the column?
We’ll start by using the number 0.433.
Step 1: Write down the formula you will be working with.
[latex]\text{PSI} = \text{ height in feet} \times 0.433[/latex]
Step 2: Cross multiply.
[latex]\dfrac{1 \text{ foot of height}}{17.78 \text{ feet of height}} = \dfrac{0.433 \text{ psi}}{\text{X psi}}[/latex]
[latex]\begin{array}{c} 1 \times \text{X} &= 17.78 \times 0.433 \\ \text{X} &= 17.78 \times 0.433 \\ \text{X} &= 7.70\end{array}[/latex]
[latex]\text{answer} = 7.70 \text{ psi}[/latex]
Now we’ll move onto using the number 2.31 and see if we get the same answer.
Step 1: Write down the formula you will be working with.
[latex]\text{PSI} = \dfrac{\text{height}}{2.31}[/latex]
Step 2: Cross multiply.
[latex]\dfrac{2.31 \text{ foot of height}}{17.78 \text{ feet of height}} = \dfrac{1 \text{ psi}}{\text{X psi}}[/latex]
[latex]1 \times 17.78 = \text{X} \times 2.31[/latex]
[latex]\begin{array}{c} \text{X} &= \dfrac{17.78}{2.31} \\ \text{X} &= 7.70\end{array}[/latex]
[latex]\text{answer} = 7.70 \text{ psi}[/latex]
Note the minor difference in the way the formula is set up. In the first scenario we took the height and MULTIPLIED it by 0.433 while in the second scenario we took the height and DIVIDED it by 2.31.
This is due to the fact that it takes 2.31 feet of head to create 1 psi. Mathematically this means that any height that we have has to be divided by 2.31 in order to get psi.
The other way is simply accounting for the fact that every foot of head gives us 0.433 psi so we end up multiplying to get the proper psi.

Why are we going through this concept with a little extra zest you ask?
The answer lies in the fact that we end up using psi quite often in the trades. More importantly we end up using water as the driving force behind calculating psi.

Industries such as pump manufacturers differentiate pumps by their ability to move water to different heights as well as there ability to create pressure.
Pump specifications can be determined in either psi or feet of head. Being able to translate back and forth between the two will help guide you in pump selection.
If you want to know more about pumps and specifications hit the following link: Pumps & Circulators. You can scroll through the website and check out different pumps, their applications and their specifications
Let’s break it down even further. Remember that one foot equals 12 inches. This means that 2.31 feet would equal 27.72 inches.
What we’ve created is another relationship between water, psi and height.
[latex]1 \text{ PSI}[/latex]
[latex]=[/latex]
[latex]2.31 \text{ feet of head}[/latex]
[latex]=[/latex]
[latex]27.72 \text{ inches water column}[/latex]
Note that we can also write down 27.72 inches of water column as 27.72″ w.c.
Now you might be asking yourself “Where would we use inches of water column to measure pressure?” It’s a good question. We can all visualise using psi to measure water pressure as we fill piping systems up with water for testing purposes but once we get down to inches water column we really are getting to small increments.

In the gas fitting trade the gas pressure sent to appliances can often be quite small. In fact when the gas finally gets to most residential appliances the pressure is well below 1 psi. So instead of saying that the pressure is 0.25 psi or 0.17 psi we break the feet down into inches and refer to pressure in terms of inches of water column.
For example the most common gas pressure that residential gas fired appliances deal with once the gas gets through the gas valve and into the burners is 3.5 inches of water column. We might also see it written as:
[latex]3.5" \text{w.c.}[/latex]
Example
How many psi are there in 3.5” w.c.?
Step 1: Write down the formula you’ll be working with.
[latex]1 \text{ PSI} = 27.72" \text{ w.c.}[/latex]
Step 2: Cross multiply.
[latex]\dfrac{1 \text{ PSI}}{\text{X PSI}} = \dfrac{27.72" \text{ w.c.}}{3.5"\text{ w.c.}}[/latex]
[latex]1 \times 3.5 = \text{X} \times 27.72[/latex]
[latex]\begin{array}{c} \text{X} &= \dfrac{3.5}{27.72} \\ \text{X} &= 0.126\end{array}[/latex]
[latex]\text{answer} = 0.126 \text{ PSI}[/latex]
What you can see from this answer is that it’s far easier to deal with gas pressures in this particular situation using inches of water column rather than PSI. Reading 3.5 inches of water column on a pressure gauge is easier to comprehend than reading 0.126 psi even through they refer to the same pressure.
In the end what we have is another way to describe the pressure in systems using water as our guiding force.

Why don’t we just go through a quick little recap of all the numbers we’ve now dealt with in this section.

Try a couple practice questions on your own. Make sure to check the video answer below each question once you are done.
Practice Questions
Question 1

Marcus has installed drainage piping in a building and now he’s required to test that piping by filling it up with water. He knows that the couplings he’s using to hold the pipe together can handle about 15 psi. The piping he’s testing runs through 3 stories for a total of 32 feet. Can the coupling at the base of the piping run handle the pressure from the water within the pipe?
Question 2

Grace is a gas fitter for a golf course in the West Kootenay region of British Columbia. They are looking to add a new boiler to the system. The boiler will be run using propane and the pressure from the gas regulator is required to be 11 inches of water column. Assuming water as our pressure measuring standard what is the pressure in pounds per square inch.
Image Descriptions
Figure 7.1: A flow chart showing the relationship between all the numbers associated with pressure when dealing with water.
- Started by taking water and filling up a pipe one foot in height
- What we ended up with was: 1 foot = 0.433 psi
- Then we filled the pipe up to get to 1 psi of pressure
- What we ended up with was: 1 psi = 2.31 feet of head
- We then translated 2.31 feet into inches: 2.31 feet = 27.72 inches
- This then leads up to the fact that: 1 psi = 27.72″ w.c. [Return to image]