Capacities
4 Weight of Water
Click play on the following audio player to listen along as you read this section.
Have you ever taken a container and filled it with water then lifted it and then realised that it weighs more than you think? If you’ve done this before then you realise that water itself is quite heavy.
The picture above is the same fish tank from a previous example. We spent the last couple sections figuring out the number of gallons or litres given cubic volume. Now our goal becomes figuring out the weight of the water contained in objects such as a fish tank.
Knowing the capacity of an object as well as the weight of water needed to fill that object is helpful in the pipefitting trade. For example let’s say that you a have a 40 U.S. gallon hot water tank. How much would it weigh once it was filled with water? If you needed to move the tank would you rather have the tank full of water or empty? Knowing the weight of the water in the tank might help you make your decision.
The weight of water changes slightly due to the temperature of the water. Actually it’s not the weight of the water that changes but the density of the water. The molecules weigh the same but the number of molecules in a given space changes. Cold water weighs more than warm water due to the fact that in the warm water the molecules are moving around faster and end up being farther apart from each other. Take a look at the picture below.
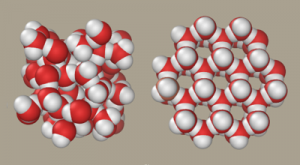
The two pictures represent water molecules bonding together. The picture on the left is an example of cold water molecules while the picture on the right is an example of warm water molecules. If you were to take an imperial gallon of cold water and weigh it, it would weigh more than an imperial gallon of warm water due to the larger separation of the molecules in the warm water.
Okay, now that we’ve gotten that out of the way we need a starting point and that starting point will be the weight of a cubic foot of water. Anyone want to guess how much one cubic foot of water weighs?
Mark: Hey Chad, how much do you think the water weighs in this cubic foot filled with
water?
Chad: No idea. I’m an electrician and not a plumber.
Mark: Good point. If anyone ever asks you this question in the future you can tell them that 1 cubic foot filled with water weighs 62.4 pounds.
Chad: Wow. That’s more that I would figure. It doesn’t look that heavy.
Mark: Exactly. It’s a little deceptive. That’s why it’s important to take into the account
the weight of water when dealing with piping or other vessels which are filled with
water.
Note part 1: Mark is the guy on the left having a bad hair day and Chad is the guy on the right with the toque.
Note part 2: After Mark taught Chad all about the weight of water they decided to check out the weight of beer and headed to local pub. They didn’t figure anything out about the weight of beer but they did find out the pub had good beer.
Our first number and basically the starting point for all this is:
[latex]1 \text{ cubic foot of water} = 62.4 \text{ pounds}[/latex]
From that number we can derive the weight of an imperial gallon, a U.S. gallon and a litre using the relationship between those numbers and cubic feet.
[latex]\begin{array}{c} 1 \text{ imperial gallon} &= 0.160 ft^3 \\ 1 \text{ U.S. gallon} &= 0.133 ft^3 \\ 1 \text{ litre} &= 0.353 ft^3 \end{array}[/latex]
At this point you have probably developed some pretty slick math skills. Try using those numbers above to derive the weight of an imperial gallon, a U.S. gallon and a litre in pounds.
Check out the video answer below to see if you were correct.
Let’s go through one last math conversion. Now that you’ve figured out litre of water weighs 2.2 pounds, how many kilograms is that.
Back a few chapters ago we figured out that 1 kilogram = 2.2 pounds so in the end of the day 1 litre = 1 kilogram.
How handy is that! The logic then goes that if 1 litre = 1 kilogram and there are 1000 litres in a cubic meter then 1 cubic meter filled with water weighs 1000 kilograms.
This is why working with metric can be so much easier than imperial. Once again everything revolves are the number 10.
Before we go on to some practice questions let’s put all the numbers together one last time.
[latex]1 \text{ cubic foot} = 62.4 \text{ lbs}[/latex]
[latex]1 \text{ imperial gallon} = 10 \text{ lbs}[/latex]
[latex]1 \text{ U.S. gallon} = 8.33 \text{ lbs}[/latex]
[latex]1 \text{ litre} = 2.2 \text{ lbs (1 kg)}[/latex]
Use the information above for the following examples. You’ll need the weight of an imperial gallon of water as well as the weight of a U.S. gallon of water.
Examples
A hot water tank contains 30 imperial gallons. What is the weight of the water in the tank when fully filled?
Step 1: Write down the relationship you will be working with.
[latex]1 \text{ imperial gallon} = 10 \text{ pounds}[/latex]
Step 2: Cross multiply.
[latex]\dfrac{1 \text{ imperial gallon}}{30 \text{ imperial gallons}} = \dfrac{10 \text{ pounds}}{\text{X pounds}}[/latex]
[latex]\begin{array}{c} 1 \times \text{X} &= 30 \times 10 \\ \text{X} &= 300\end{array}[/latex]
[latex]\text{answer} = 300 \text{ pounds}[/latex]
Examples
We’ll make this easy and stick with our hot water tank example except this time the weight of the water in the tank is 333 pounds. Calculate the number of U.S. gallons in the tank.
Step 1: Write down the relationship you will be working with.
[latex]1 \text{ U.S. gallons} = 8.33 \text{ pounds}[/latex]
Step 2: Cross multiply.
[latex]\dfrac{1 \text{ U.S. gallon}}{\text{X U.S. gallons}} = \dfrac{8.33 \text{ pounds}}{333\text{ pounds}}[/latex]
[latex]1 \times 333 = \text{X} \times 8.33[/latex]
[latex]\begin{array}{c} \text{X} &= \dfrac{333}{8.33} \\ \text{X} &= 39.98\end{array}[/latex]
[latex]\text{answer} = 39.98 \text{ U.S. gallons}[/latex]
Now try a couple practice questions on your own. Make sure to check the video answer below each question once you are done.
Practice Questions
Question 1
Billie the boiler maker is filling up a boiler with water. The boiler itself weighs 200 pounds and the boiler holds 25 imperial gallons of water. How much is the total weight of the boiler and the water in the boiler.
Question 2
Dexter installs pools for a living in Las Vegas. He is currently installing a pool on the roof of a 3 story house. The pool is 20 feet long by 10 feet wide by 5 feet deep. He is required to tell the engineer how much water the pool will hold in pounds when completely filled. Calculate the weight of the water in pounds using U.S. gallons as your reference. Remember that you’ll first have to calculate the volume of the pool in cubic feet and then translate to U.S. gallons before getting your final answer.
