Trigonometry
18 Using Trigonometry to Find Angles
Click play on the following audio player to listen along as you read this section.
In the last section we used trigonometry to find the length of different sides of a right triangle given an identified angle and the length of one side. Now we approach it from a different angle. We’ll have situations where we are given two of the side lengths and maybe all three. The unknown will now be the identified angle. We’ll know which angle it is but we won’t know the value of that angle in degrees.
First things first. Let’s put up the SOH CAH TOA formulas just to remind us what we’re working with.
| SOH | CAH | TOA |
| [latex]\text{Sine } \theta = \dfrac{\text{opposite}}{\text{hypotenuse}}[/latex] | [latex]\text{Cosine } \theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}[/latex] | [latex]\text{Tangent } \theta = \dfrac{\text{opposite}}{\text{adjacent}}[/latex] |
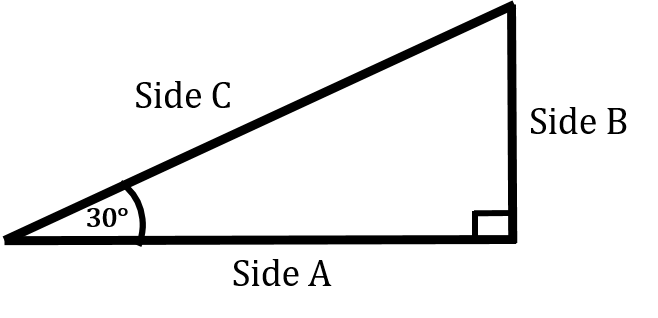
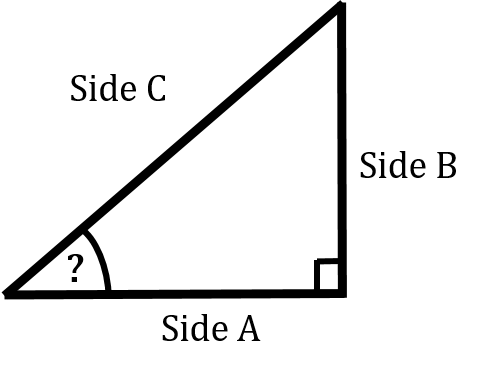
What we learned previously was that the identified angle created a relationship between the sides. If we had an angle of 30 degrees then that would dictate the relationship between the opposite, adjacent and hypotenuse sides. If we know one of the sides in the following diagram we could find the other two sides given that the identified and is 30 degrees.
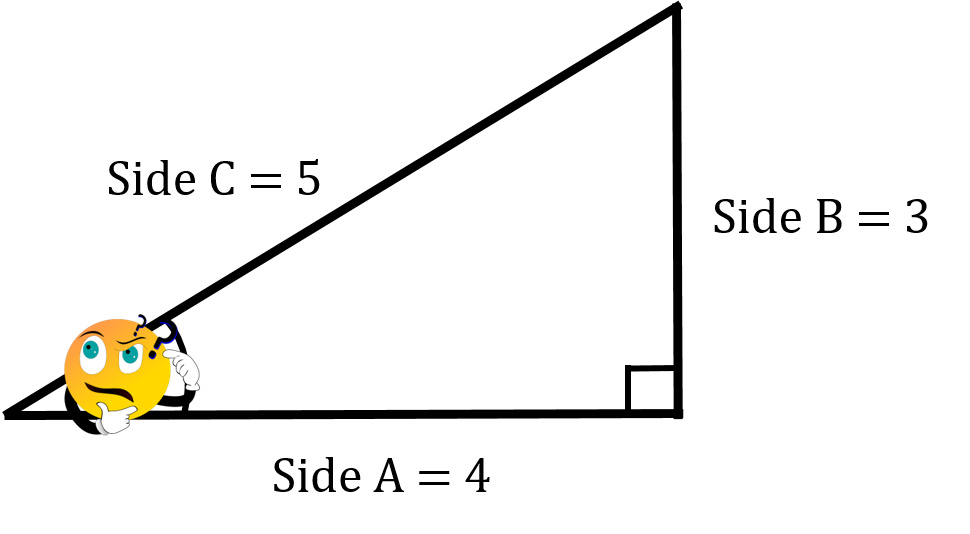
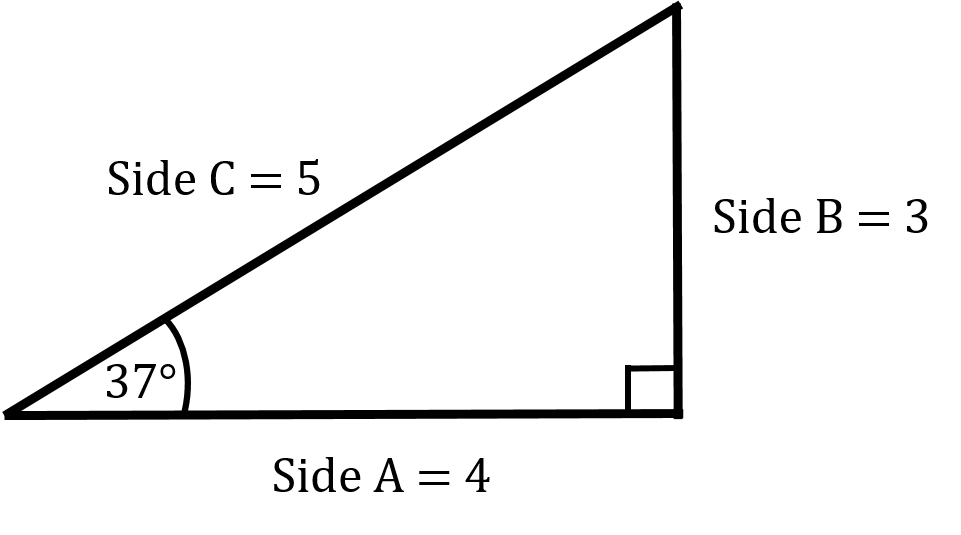
We are now doing the reverse. We’ll know the sides so we can calculate the relationship between them but then we have to translate that relationship into an angle. That’s the new goal. Take a look at the drawing below to see what I mean.
Let’s use the drawing above and go through the thought process.
We know all three sides so technically we can use any of the three formulas to work with. For our purposes we’ll go with the sine function.
[latex]\text{Sine } \theta = \dfrac{\text{opposite}}{\text{hypotenuse}}[/latex]
We know that the opposite side is 3 and the hypotenuse is 5 so we can go ahead and plug in those numbers.
[latex]\begin{equation}\begin{split} \text{Sine } \theta &= \dfrac{\text{opposite}}{\text{hypotenuse}} \\ \text{Sine } \theta &= \dfrac{3}{5} \\ \text{Sine } \theta &= 0.6\end{split}\end{equation}[/latex]
We’ve calculated that the relationship between the opposite and the hypotenuse is 0.6. The opposite is 0.6 times the length of the hypotenuse given the identified angle. The question then becomes “What is the value of the identified angle?”

This is where we need to go back to our calculator.
How does this work on our calculator? When we used the sine, cosine or tangent function combined with the identified angle we were able to get the relationship between sides.
Now we take that relationship and plug it into the calculator to get the identified angle. This is the point where things may get a bit tricky depending on what type of calculator you have.
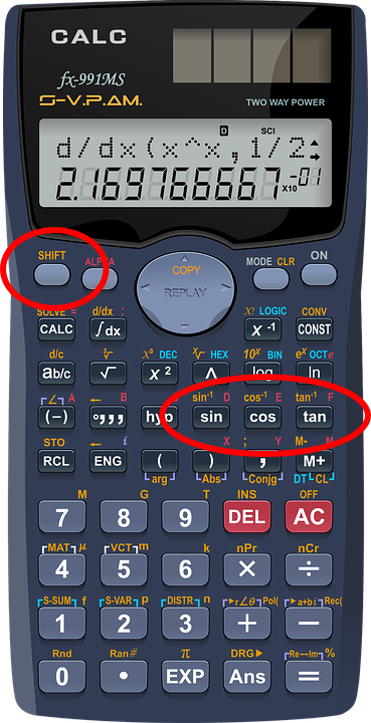
For most of us it should work something like the following. If you take a look at your calculator you’ll have a number of functions on it. Included in those function is the sine, cosine and tangent buttons. What you’ll also notice is that you have either a second function or a shift button.
If you go and press that “shift” or “second function” button what you’ll end up doing is taking those functions including the sine, cosine and tangent functions and using them for another function. Hence the name second function. In this case what you end up doing is shifting from sine, cosine and tangent to sine-1, cosine-1 or tangent-1. We are essentially reversing the process.
Okay great but what exactly does that do for us? Once we get into that second function mode we can take the relationship between the two sides and work backwards to find the identified angle. Let’s use the example up above to see what I mean.
[latex]\begin{equation}\begin{split} \text{Sine } \theta &= \dfrac{\text{opposite}}{\text{hypotenuse}} \\ \text{Sine } \theta &= \dfrac{3}{5} \\ \text{Sine } \theta &= 0.6\end{split}\end{equation}[/latex]
We’ve calculated that the relationship between the opposite and the hypotenuse is 0.6. We can then use the sine function, or more specifically the sin-1 function to find the identified angle. Now what we need to plug into the calculator is as follows. We start by pressing the shift or second function button. This changes sin to sin-1. Now press the sin button. Then finish it off by entering in 0.6. What do you get?
[latex]sin^{-1}0.6 = 36.87[/latex]
We can round this up to 37. What we have just determined is that if the relationship between the opposite and the hypotenuse is 0.6 then the angle needed to generate that (the identified angle) is 37 degrees.
 [latex]\begin{equation}\begin{split} \text{Sine } \theta &= \dfrac{\text{opposite}}{\text{hypotenuse}} \\ \text{Sine } \theta &= \dfrac{3}{5} \\ \text{Sine } \theta &= 0.6\end{split}\end{equation}[/latex]
[latex]\begin{equation}\begin{split} \text{Sine } \theta &= \dfrac{\text{opposite}}{\text{hypotenuse}} \\ \text{Sine } \theta &= \dfrac{3}{5} \\ \text{Sine } \theta &= 0.6\end{split}\end{equation}[/latex]
Let’s go through another example.
Example
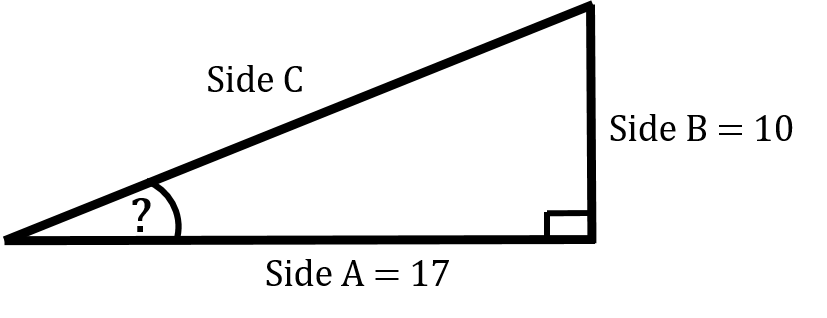
Find the identified angle if Side A is 17 and Side B is 10.
Step 1: Determine which of the three trigonometry functions you’ll be working with. In this case we have the opposite and the adjacent sides so we’ll work with the tangent function.
[latex]\text{tangent } \theta = \dfrac{\text{opposite}}{\text{adjacent}}[/latex]
Step 2: Plug in the numbers and calculate.
[latex]\begin{array}{c} \text{tangent } \theta &= \dfrac{\text{opposite}}{\text{adjacent}} \\ \text{tangent } \theta &= \dfrac{10}{17} \\ \text{tangent } \theta &= 0.588 \end{array}[/latex]
Step 3: Take this number and plug it into our calculator using the tan-1 function.
[latex]\text{tangent }34.55^\circ = 0.588[/latex]
We can round this up to 35 degrees to make things easier.
Example
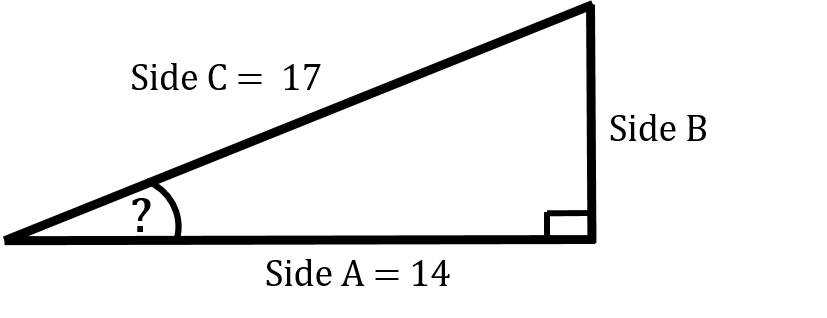 Find the identified angle if Side A is 14 and Side C is 17.
Find the identified angle if Side A is 14 and Side C is 17.
Step 1: Determine which of the three trigonometry functions you’ll be working with. In this case we have both the adjacent side and the hypotenuse so we will work with the cosine function.
[latex]\text{cosine } \theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}[/latex]
Step 2: Plug in the numbers and calculate.
[latex]\begin{array}{c} \text{cosine } \theta &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\ \text{cosine } \theta &= \dfrac{14}{17} \\ \text{cosine } \theta &= 0.823 \end{array}[/latex]
Step 3: Take this number and plug it into our calculator using the cos-1 function.
[latex]\text{cosine }34.61^\circ = 0.823[/latex]
Once again we can round this up to 35 degrees to make things easier.
Now try a couple questions for yourself. Make sure to check the video answers once you are done.