Trigonometry
16 Introduction to Trigonometry
Click play on the following audio player to listen along as you read this section.
In the last section we took a look at the basics of triangles. We used the Pythagorean theorem to solve for any side of a right triangle. The only requirement was that we know what the length of the other two sides were.
When using the Pythagorean theorem we didn’t need to know any of the angles within the triangle. The only thing we needed to make sure was that one of the angles was a right angle.
Take a look at the drawing below. It shows a right triangle with the other two angles both being forty five degrees.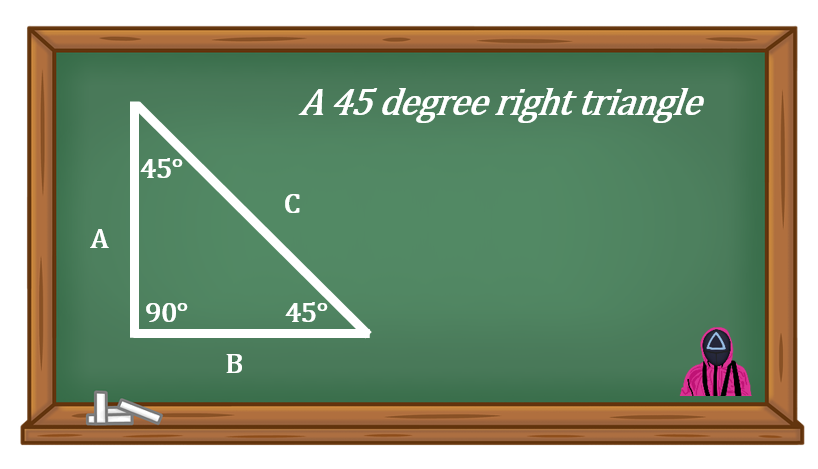
This is a special triangle when dealing with the construction trades. When piping is offset it’s quite often done using forty five degree fittings. What we end up making is this special version of a triangle.
Some of you may already have run across this in either your studies or even in the field. What you might remember is that side “C” is 1.414 times larger than either side “A” or side “B”.
So how did we determine that? Well that number comes from trigonometry. It is also the case that side A and B are equal.
Trigonometry is a system which allows us to calculate the values of any angle or side in a right triangle. It deals with more than what Pythagoras figured out when dealing with triangles.
Given enough information we can find any of the angles or any of the sides. Trigonometry allows us to work with triangles to a much greater extent than we have being doing up to this point.
The Relationship between the Sides and Angles in a Right Triangle
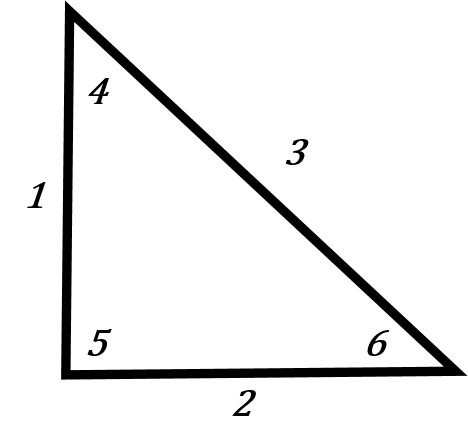
We noted in the last chapter that there are six pieces of information in a right triangle. There are the three sides and the three angles. The only thing we know for sure is that one of the angles is 90 degrees. So in this case number 5 is a given at 90 degrees.
When working with trigonometry it is required that you have 3 of those 6 pieces of information given in order to figure out the other three. As just stated one of the three is the 90 degree angle. Essentially you need the 90 degree plus two other pieces of information.
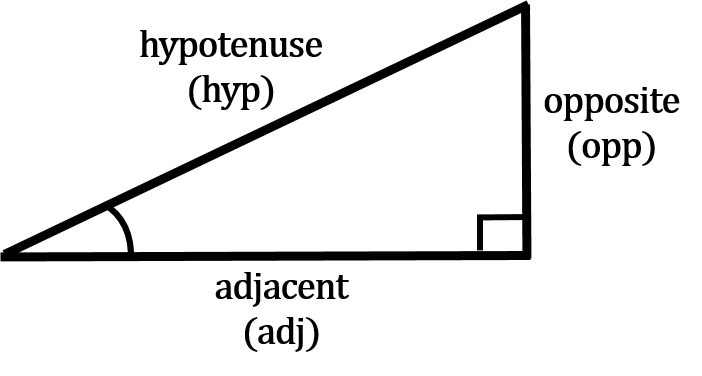
Remember we also named the three sides of the triangle depending on the angle of reference. The names become very important when dealing with trigonometry. They end up defining how we go about finding the unknown variable.
This is an important point when dealing with trigonometry. Naming the sides of a triangle properly allows us to use the formulas in trigonometry properly. This leads us into the next part part……the angles.
The Angles
This topic might get a little tricky so pay attention.

Angles within a right triangle can be referred to by the relationship between two of the sides within that triangle. We’ll start by stating the three names that we will be working with.
Sine Cosine Tangent
It would be fair to say that these names refer more to the relationship between sides than to the actual names of the angles.
For example, sine is the relationship between the opposite side and the hypotenuse. The relationship between the two will give you a number and this number will generate an angle using a calculator.
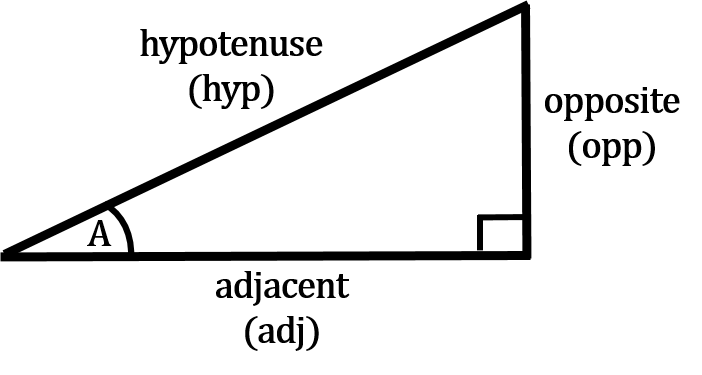
Let’s go back to our triangle with a reference angle “A” to see how this works.
Our reference angle is “A”. From this we can derive which side is the opposite, adjacent and hypotenuse.
The idea is the value of angle “A” defines the relationship between the sides.
This is where trigonometry steps in and states how everything goes together. What you end up with is the following.
SOH CAH TOA
What SOH CAH TOA defines is actually the three formulas we work with in trigonometry. We’ll break it down even further.
| SOH | CAH | TOA |
| [latex]\text{Sine } \theta = \dfrac{\text{opposite}}{\text{hypotenuse}}[/latex] | [latex]\text{Cosine } \theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}[/latex] | [latex]\text{Tangent } \theta = \dfrac{\text{opposite}}{\text{adjacent}}[/latex] |
Note: the symbol “θ” is the Greek letter theta and is used to refer to the measured angle.
If you find the relationship between the opposite side and the hypotenuse what you end up finding is the angle referred to as sine.
Stated another way the angle of sine can be found by dividing the opposite side of the triangle by the hypotenuse.
Trigonometry is not all that complicated in the end of the day but because there are a few words (including trigonometry) that might be unfamiliar to students it sometimes seems to be just a little out of reach.
What we’ll do in the next parts of the chapter is break each of three formulas down into their basic parts and go through some examples. In the end of the day if you can just remember two things about trigonometry then you are almost there.
- Trigonometry is simply the relationship between sides and the relationship between those sides will end up telling you the angle you’re dealing with.
- SOH CAH TOA is pronounced “so……ca……toe……ah”
You’re already halfway there.