6 Mass, Weight & Newton’s Second Law
Resources
Video to Watch: Mechanical Universe: Episode 6 – Newton’s Law
Article to Read: Mathematicians solve age-old spaghetti mystery
Article to Read: Longest overhaul of scientific units since the French Revolution wins approval
Equations Introduced and Used for this Topic: (All equations can be written and solved as both scalar and vector)
- [latex]F = ma[/latex]
- [latex]w = mg[/latex]
Where…
- [latex]F[/latex] is force, measured in newtons (N)
- [latex]w[/latex] is weight (it is a force), measured in newtons (N)
- [latex]m[/latex] is mass, commonly measured in kilograms (kg), grams (g) or tonnes (t)
- [latex]a[/latex] is acceleration (deceleration is negative), measured in metres per second squared (m/s2)
- [latex]g[/latex] or [latex]a_g[/latex] is the acceleration due to gravity and varies from 9.78 m/s2 (equator) to 9.83 m/s2 (North or South Pole). The average value of gravity is taken to be either 9.80 m/s2 or 9.81 m/s2
Newton’s Laws of Motion
- Extra Help: A-Level Physics Tutor
- Article to Read: kilogram, ampere, kelvin and mole redefined
- Extra Help: Newton’s Laws
- Extra Help: The Meaning of Force
- Video to Watch: Newton’s 3rd Law of Force – Forklift Driver Causes an Entire Warehouse to Fall like Dominos
Sir Isaac Newton worked in many areas of mathematics and physics. He developed the theories of gravitation in 1666, when he was only 23 years old. Some twenty years later, in 1686, he presented his three laws of motion in the “Principia Mathematica Philosophiae Naturalis.”
Newton’s first law states that every object will remain at rest or in uniform motion in a straight line unless compelled to change its state by the action of an external force. This is normally accepted as the definition of inertia. The key point here is that if there is no net force acting on an object (if all the external forces cancel each other out) then the object will maintain a constant velocity. If that velocity is zero, then the object remains at rest. If an external force is applied, the velocity will change because of the force.
Newton’s second law explains how the velocity of an object changes when it is subjected to an external force. The law defines a force to be equal to change in momentum (mass times velocity) per change in time. Newton also developed the calculus of mathematics, and the “changes” expressed in the second law are most accurately defined in differential forms. (Calculus can also be used to determine the velocity and location variations experienced by an object subjected to an external force.) For an object with a constant mass [latex]m[/latex], the second law states that the force ([latex]F[/latex]) is the product of an object’s mass and its acceleration [latex]a[/latex]:
[latex]F = m a[/latex]
Newton’s third law states that for every action (force) in nature there is an equal and opposite reaction. In other words, if object A exerts a force on object B, then object B also exerts an equal force on object A. Notice that the forces are exerted on different objects. The third law can be used to explain the generation of lift by a wing and the production of thrust by a jet engine.
6.1 Net Force… The resolution of multiple force vectors
- Extra Help: Determining Net Force
- Extra Help: Addition of Forces
Net Force: the resolutions of multiple forces acting on a body
Forces are Vectors … They are added, subtracted and combined according to the direction they take.
Quite often, vectors are simply left as the sum of the different vectors and not recombined.
Vectors in the same direction are added and vectors in the opposite direction are subtracted.
For instance:
10 N right + 5 N right = 15 N right
(The vectors are in the same direction so they are added.)
10 N right + 5 N left = 5 N right
(The vectors are in the opposite direction so they are subtracted.)
Vectors that are angled between two directions are first broken up into the various components for those directions before they are added or subtracted.
10 N right + 5 N down = 10 N right + 5 N down
(The vectors are in different directions so they are left alone.)
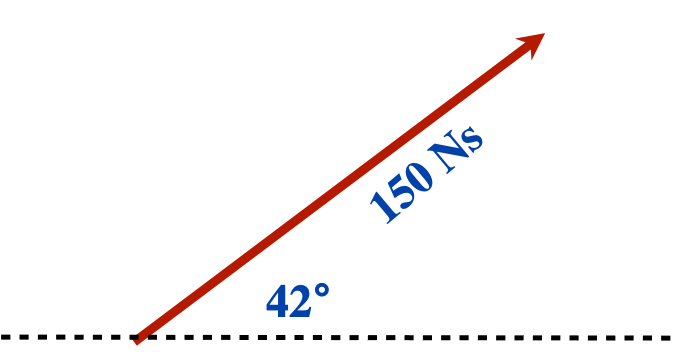
Vectors that are angled between two directions are first broken up into the various components for those directions before they are added or subtracted.
For instance:
Using right angle trigonometry this 15 N vector would be broken up into the force directed upwards and the force to the left.
To find the force upwards use the sine function:
[latex]\sin 40^{\circ} = \dfrac{\text{force up}}{15 N}[/latex]
To find the force right use the cosine function:
[latex]\cos 40^{\circ} = \dfrac{\text{force right}}{15 N}[/latex]
Example 6.1.1
Resolve the following multiple force vectors.

Solution
[latex]F_{\text{net}} = 10 \text{ N right }+10 \text{ N left }[/latex] or [latex]F_{\text{net}} = 0 \text{ N}[/latex]
Solution
[latex]F_{\text{net}} = 10 \text{ N right }+ 10\text{ N right}[/latex] or [latex]F_{\text{net}} = 20\text{ N right}[/latex]
Solution
[latex]F_{\text{net}} = 10 \text{ N right }+ 10\text{ N right }+ 10\text{ N right }[/latex] or [latex]F_{\text{net}} = 30\text{ N right}[/latex]
Solution
[latex]F_{\text{net}} = 10\text{ N right }+ 10\text{ N left }+ 10\text{ N left}[/latex] or [latex]F_{\text{net}} = 10\text{ N left}[/latex]
Solution
[latex]F_{\text{net}} = 10\text{ N right }+ 6\text{ N left }+ 6\text{ N left}[/latex] or [latex]F_{\text{net}} = 2\text{ N left}[/latex]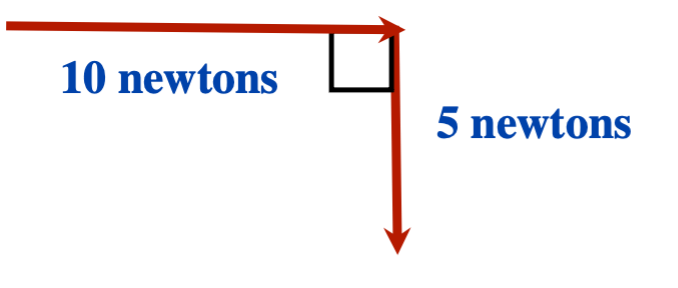
Solution
[latex]F_{\text{net}}=10\text{ N right }+5\text{ N down}[/latex]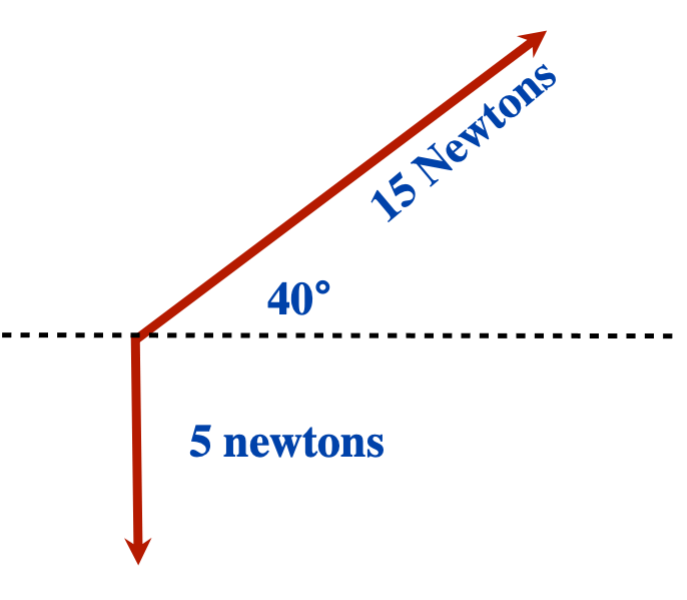
Solution
First break the 15 N force into components:- [latex]\text{Force up }= 15\text{ N }\sin 40^{\circ} \text{ or }9.6\text{ N up}[/latex]
- [latex]\text{Force right }= 15\text{ N }\cos 40^{\circ}\text{ or }11.5\text{ N right}[/latex]
Then, [latex]F_{\text{net}} = 11.5\text{ N right }+ 9.6\text{ N up }+ 5\text{ N down}[/latex] or [latex]F_{\text{net}} = 11.5\text{ N right }+ 4.6\text{ N up}[/latex]
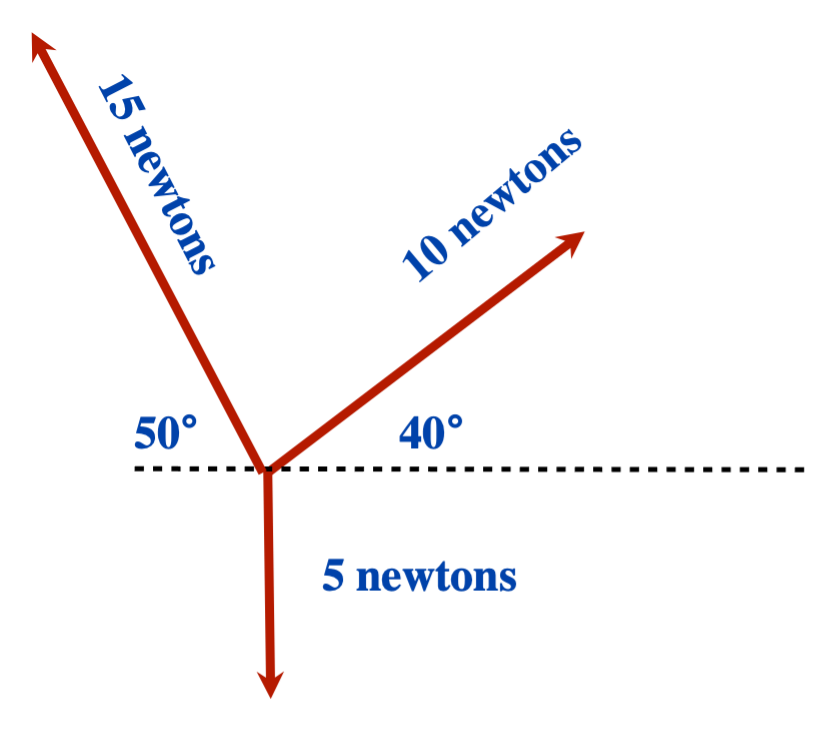
Solution
First break the 15 N force into components:- [latex]\text{Force up }= 15\text{ N }\sin 50^{\circ}\text{ or }11.5\text{ N up}[/latex]
- [latex]\text{Force left }= 15\text{ N }\cos 50^{\circ}\text{ or }9.6\text{ N left}[/latex]
Second break the 10 N force into components:
- [latex]\text{Force up }= 10\text{ N }\sin 40^{\circ}\text{ or }6.4\text{ N up}[/latex]
- [latex]\text{Force right }= 10\text{ N }\cos 40^{\circ}\text{ or }7.7\text{ N right}[/latex]
Then, [latex]F_{\text{net}} = 11.5\text{ N up }+ 6.4\text{ N up }+ 5\text{ N down }+ 9.6\text{ N left }+ 7.7\text{ N right}[/latex] or [latex]F_{\text{net}} = 12.9\text{ N up }+ 1.9\text{ N left}[/latex]
6.2 Newton’s Second Law
- Extra Help: Newton’s Second Law
- Research News: Physical kilogram is officially dead
Equations Introduced or Used for this Section:
- [latex]F = ma[/latex]
- [latex]w = mg[/latex]
- Four Kinematic Equations:
- [latex]d = \dfrac{(v_i + v_f) t}{2}[/latex]
- [latex]2ad = v_f^2 - v_i^2[/latex]
- [latex]\vec{v_f} = \vec{v_i} + \vec{a}t[/latex]
- [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
- Newton’s second law
- [latex]\vec{F} = m\vec{a}[/latex]
Data organized as:
-
- [latex]a =[/latex] Accelerated Motion
- [latex]v_i =[/latex]
- [latex]v_f =[/latex]
- [latex]d =[/latex]
- [latex]t =[/latex]
- [latex]F =[/latex] For Unbalanced Forces
- [latex]m =[/latex]
- [latex]a =[/latex]
- [latex]w =[/latex] For Weight Questions
- [latex]m =[/latex]
- [latex]g =[/latex]
Newton’s Second Law: for a Balanced or Net Force = 0
From Newton’s second law: if the external forces acting on an object are balanced
([latex]F_{\text{Net}} = 0[/latex]) then the object experiences no acceleration.
This means for [latex]F_{\text{Net}} = 0[/latex], [latex]a=0\text{ m/s}^2[/latex]. Therefore, if at rest, it remains at rest ([latex]v = 0 \text{ m/s}[/latex]) or if in motion, then it remains in that constant state of motion ([latex]v = \text{ constant}[/latex]).
Newton’s Second Law: for an Unbalanced or Net Force ≠ 0
From Newton’s second law: if the external forces acting on an object are unbalanced
([latex]F_{\text{Net}} \neq 0[/latex]) then the object will experience some amount of acceleration.
This means for [latex]F_{\text{Net}} \neq 0[/latex], [latex]a \neq 0 \text{ m/s}^2[/latex]. Therefore, if originally at rest, it will accelerate and begin to move ([latex]v \neq 0 \text{ m/s}[/latex]) or if is already in motion then it will be changing its speed or velocity ([latex]v \neq \text{ constant}[/latex]).
Analyzing this change in motion resulting from an unbalanced force acting on an object requires one to use an equation derived from Newton’s second law:
[latex]F = m a[/latex]
Using Newton’s second law often requires one to share the acceleration measure with the four kinematic equations, as you will see in the following examples.
- Four Kinematic Equations:
- [latex]d = \dfrac{(v_i + v_f) t}{2}[/latex]
- [latex]2ad = v_f^2 - v_i^2[/latex]
- [latex]\vec{v_f} = \vec{v_i} + \vec{a}t[/latex]
- [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
- Newton’s second law
- [latex]\vec{F} = m \vec{a}[/latex]
Example 6.2.1
Answer the following questions:
- A 54 kg diver is standing on a diving board ready to dive. What unbalanced force acts upon him?
Solution
The weight of the diver is balanced by the support of the diving board. Therefore, the unbalanced force = 0 N. - A 54 kg diver is standing on a diving board ready to dive. What balanced force acts upon him?
Solution
The weight of the diver is balanced by the support of the diving board. Therefore, the balanced force = weight where [latex]w = m g[/latex].- balanced force = (54 kg)(9.8 m/s2)
- balanced force = 529 N
- If this 54 kg diver steps off the diving board, what unbalanced force acts upon him?
Solution
The weight of the diver is not balanced by the support of the diving board. Therefore, the diver is accelerated downwards by gravity where [latex]F = m a_g[/latex].- unbalanced force (F) = (54 kg)(9.8 m/s2)
- unbalanced force (F) = 529 N
- If this 54 kg diver steps off the diving board, what balanced force acts upon him?
Solution
The weight of the diver is not balanced by the support of the diving board. Therefore, the balanced force acting on the diver is 0 N.
Example 6.2.2
An unbalanced force of 84 N gives an object of unknown mass an acceleration of 4.2 m/s2. What is the mass of this unknown object?
Solution
Data:
- [latex]F = 84 \text{ N}[/latex]
- [latex]m = \text{ Find}[/latex]
- [latex]a = 4.2 \text{ m/s}^2[/latex]
Solution:
- [latex]F = m a[/latex]
- [latex]84 \text{ N } = m (4.2 \text{ m/s}^2)[/latex]
- [latex]m = 20 \text{ kg}[/latex]
Example 6.2.3
An unbalanced force of 500 N acts upon a 20 kg object. At what rate does this object accelerate?
Solution
Data:
- [latex]F = 500 \text{ N}[/latex]
- [latex]m = 20 \text{ kg}[/latex]
- [latex]a = \text{ Find}[/latex]
Solution:
- [latex]F = m a[/latex]
- [latex]500 \text{ N } = (20 \text{ kg})a[/latex]
- [latex]a = 25 \text{ m/s}^2[/latex]
Example 6.2.4
A 80 tonne passenger jet decelerates at 1.5 gs when landing. What braking force is acting on it?
Solution
Conversions:
- 80 tonnes = 80000 kg
- 1.5 g’s = 1.5(9.8 m/s2) = 14.7 m/s2
Data:
- [latex]F = \text{ Find}[/latex]
- [latex]m = 80 \text{ tonnes}[/latex]
- [latex]a = 1.5 \text{ g's}[/latex]
Solution:
- [latex]F = m a[/latex]
- [latex]F = (80000 \text{ kg})(14.7 \text{ m/s}^2)[/latex]
- [latex]F =[/latex] 1176000 N (≈ 1.2 × 106 N)
Exercise 6.2
- A 62 kg diver is standing on a diving board ready to dive. What unbalanced force acts upon him?
- If this 62 kg diver steps off the diving board, what unbalanced force acts upon him?
- An unbalanced force of 18 N gives an object of unknown mass an acceleration of 2.5 m/s2. What is the mass of this unknown object?
- An unbalanced force of 500 N acts upon a 40 kg object. At what rate does this object accelerate?
- What is the force of a spring toy that accelerates a 50 g mass at 2.0 cm/s2?
- What is the acceleration of a 75 kg skydiver if the air resistance acting at that part of the fall is 420 N?
- Suppose a spring loaded toy is released and accelerates two masses in opposite directions. If the smaller mass of 15 g accelerates at 8.0 cm/s2, at what rate does the larger 35 g mass accelerate in the opposite direction?
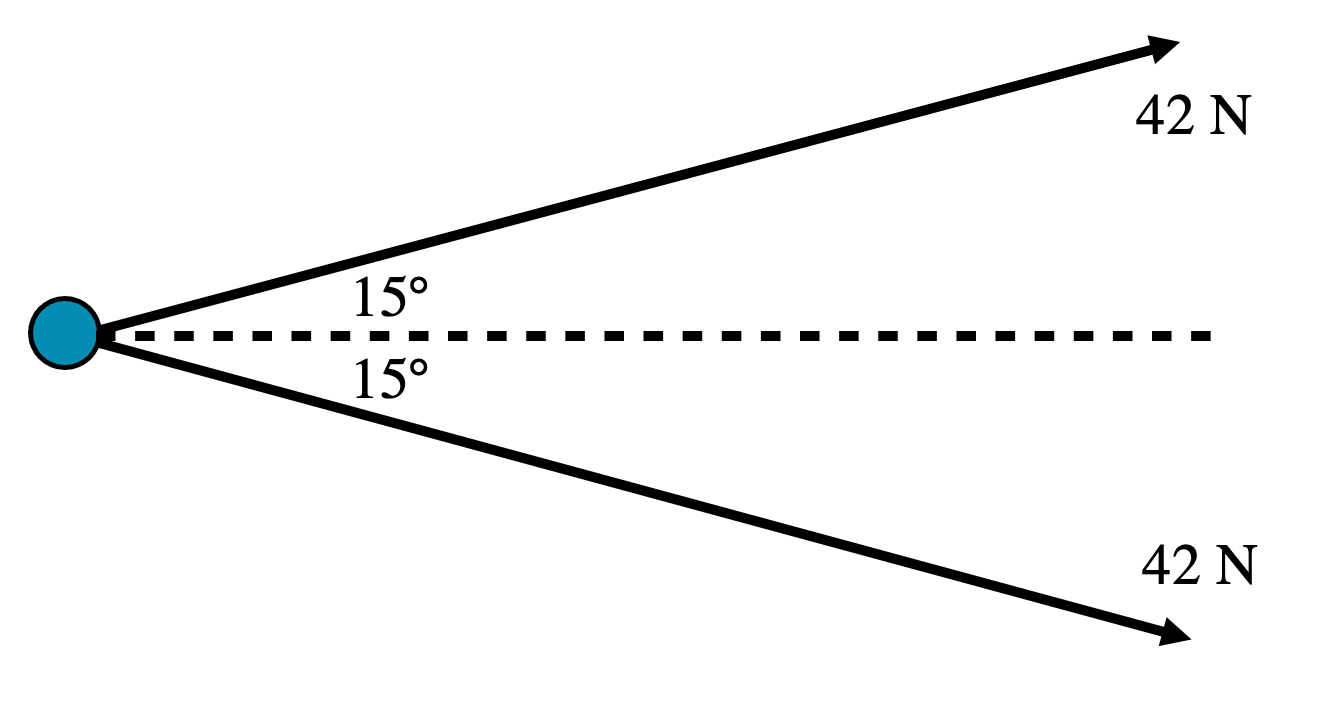
- A slingshot device is launching an 85 g steel sphere by using two angled forces as shown below. At what rate does the steel sphere accelerate?
6.3 Weight & Mass
- Article to Read: Lakes of Melted Snow Are Literally Bending Antarctica’s Ice Shelves in Half
- Article to Read: Is this the most massive star in the universe?
Equations Introduced or Used for this Section:
- [latex]F = ma[/latex]
- [latex]w = mg[/latex]
- Four Kinematic Equations:
- [latex]d = \dfrac{(v_i + v_f) t}{2}[/latex]
- [latex]2ad = v_f^2 - v_i^2[/latex]
- [latex]\vec{v_f} = \vec{v_i} + \vec{a}t[/latex]
- [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
- Constant Velocity Equation
- [latex]\vec{v} = \dfrac{\vec{d}}{t}[/latex]
Weight and mass are concepts that many students confuse in their early studies.
The mass of an object refers to the measure of the amount of matter that exists in that object and the SI measure of it is in kilograms (kg)[1]. This amount of matter remains constant anywhere in the universe and is one of the fundamental measurements in physics. At high enough speeds, relativity will increase the mass by an amount called the relativistic mass.
The weight of an object is a measure of the force of gravity that acts on the object. This can be tricky to measure as this measure is typically done by placing a scale between the object and the surface it is resting on. If the object the scale in between and the surface the scale is resting on are all in a state of free fall, then the scale can read 0 N since there is no net force holding the object to the surface. One can generally experience this temporary weightlessness in free fall amusement park rides. As such, astronauts in space, along with their spaceship, are weightless in their orbit around the Earth as they are always in that state of free fall.
weight = mass × gravity
Weight, like other forces, is measured in newtons.
When one measures the weight of an object in an elevator, one is required to look at weight as the measure of the sum or difference of the acceleration of gravity and of the surface the object is resting on. Consider the following example, where the acceleration of an elevator is 4.2 m/s2.
For an elevator at rest, the weight of the object is a simple measure, specifically, its weight is the product of mass × gravity.
[latex]w = m a_g[/latex]
&
[latex]w = m (9.8 \text{ m/s}^2)[/latex]

If we are now trying to measure the weight of an object on a floor that is accelerating downwards we would measure the weight to be less, which is similar to how we can feel lighter in an elevator that starts to accelerate downwards. The measured weight in this case would be the acceleration of gravity minus the acceleration of the falling floor.
[latex]w = m (a_g - a_{\text{floor}})[/latex]
&
[latex]w = m (9.8 \text{ m/s}^2 - 4.2 \text{ m/s}^2)[/latex] or [latex]w = m (5.6 \text{ m/s}^2)[/latex]
If we are now trying to measure the weight of an object on a floor that is accelerating upwards we would measure the weight to be greater which is similar to how we can feel heavier in an elevator that starts to accelerate upwards. The measured weight in this case would be the acceleration of gravity plus the acceleration of the falling floor.
[latex]w = m (a_g + a_{\text{floor}})[/latex]
&
[latex]w = m (9.8 \text{ m/s}^2 + 4.2 \text{ m/s}^2)[/latex] or [latex]w = m (14 \text{ m/s}^2)[/latex]
The following examples illustrate the difference between of weight and mass.
Example 6.3.1
Answer the following questions:
- Find the weight of a truck whose mass is 1200 kg.
- What is the acceleration of this truck if an unbalanced force of 4200 N is placed on it.
Solution
Question (i):
- Data:
- [latex]w = \text{ Find}[/latex]
- [latex]m = 1200 \text{ kg}[/latex]
- [latex]g = 9.8 \text{ m/s}^2[/latex]
- Solution
- [latex]w = m g[/latex]
- [latex]w = (1200 \text{ kg})(9.8 \text{ m/s}^2)[/latex]
- [latex]w = 11760 \text{ N or } 11800 \text{ N}[/latex]
Question (ii):
- Data:
- [latex]F = 4200 \text{ N}[/latex]
- [latex]m = 1200 \text{ kg}[/latex]
- [latex]a = \text{ Find}[/latex]
- Solution:
- [latex]F = m a[/latex]
- [latex]4200 \text{ N } = (1200 \text{ kg}) a[/latex]
- [latex]a = 4200 \text{ N } \div 1200 \text{ kg}[/latex]
- [latex]a = 3.5 \text{ m/s}^2[/latex]
Example 6.3.2
What is the mass of the 185 kg NASA Mars Rover currently resting on the Martian surface, where the Martian gravity is 3.711 m/s2?
Solution
The mass of the NASA Mars Rover remains constant at 185 kg no matter where it is. The weight of it will change according to the strength of gravity.
Example 6.3.3
A net force of 180 N acts on a 20 kg mass for 4.0 s. If this mass was originally at rest:
- What final speed did it reach?
- How far did it travel during these 4.0 s?
Solution
Data:
- [latex]a = \text{ need}[/latex]
- [latex]v_i = 0 \text{ m/s}[/latex]
- [latex]v_f = \text{ Find for Question (i)}[/latex]
- [latex]d = \text{ Find for Question (ii)}[/latex]
- [latex]t = 4.0 \text{ s}[/latex]
- [latex]F = 180 \text{ N}[/latex]
- [latex]m = 20 \text{ mg}[/latex]
- [latex]a = \text{ Find for Question (i)}[/latex]
First, find the acceleration:
- [latex]F = m a[/latex]
- [latex]180 \text{ N } = (20 \text{ kg}) a[/latex]
- [latex]a = 180 \text{ N } \div 20 \text{ kg}[/latex]
- [latex]a = 9.0 \text{ m/s}^2[/latex]
Question (i):
For this question assume that the distance travelled is not asked for. Therefore we will use the equation:
- [latex]v_f = v_i + a t[/latex]
- [latex]v_f = 0 \text{ m/s } + (9.0 \text{ m/s}^2)(4.0 \text{ s})[/latex]
- [latex]v_f = 36 \text{ m/s}[/latex]
Question (ii):
For this equation assume that the final speed is not asked for. Therefore we will use the equation:
- [latex]d = v_i t + \frac{1}{2} a t^2[/latex]
- [latex]d = (0 \text{ m/s})(4.0 \text{ s}) + \frac{1}{2}(9.0 \text{ m/s}^2)(4.0 \text{ s})^2[/latex]
- [latex]d = 72 \text{ m}[/latex]
Exercise 6.3
- Find the weight of an object whose mass is 15 kg and the acceleration of this object if an unbalanced force of 450 N is placed on it.
- An unbalanced force of 50 N is placed upon two different bodies; one whose mass is 10 kg and the other whose weight is 10 N. What would be their respective accelerations?
- What is the weight of a 55 kg person standing at the Earth’s equator? What would be this same person’s weight at the South pole?
- What is the mass of an 76 kg astronaut standing on the surface of a planet where the acceleration due to gravity is 22.5 m/s2?
- What unbalanced force is needed to give an object of weight 100 N an acceleration of 2.5 gs?
- If a 74 kg skydiver reaches a terminal velocity of 120 km/h, what must be the air resistance acting on this person at this speed? If this diver changes from a spread eagle to a dive position and reaches a terminal velocity of 180 km/h, what is the air resistance acting on this person at this speed?
- A 50 kg stunt person is suspended by several fine wires (invisible to the camera) that are exerting a force of 420 N upwards on this person. At what rate is this person accelerating and in what direction?
- Suppose a person is using a rope that can only support 95% of their weight. At what rate would this person have to accelerate, sliding down the rope so that it does not break?
- A 1200 kg elevator that has a maximum load capacity of 2000 kg is designed to accelerate at 0.15 m/s2. What range in force could the cables running this elevator experience if operated within the 2000 kg load capacity? (Tricky)
6.4 Newton’s Second Law & Accelerated Motion
Newton’s second law[2], most commonly seen as [latex]F = ma[/latex] (scalar form) relates the amount of acceleration that results from an unbalanced force that acts on an object. Using this new approach to measure acceleration, we are able to expand the situations where constant acceleration occurs, and in our analysis of these problems while using the four kinematic
- Four Kinematic Equations:
- [latex]d = \dfrac{(v_i + v_f) t}{2}[/latex]
- [latex]2ad = v_f^2 - v_i^2[/latex]
- [latex]\vec{v_f} = \vec{v_i} + \vec{a}t[/latex]
- [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
- Newton’s second law
- [latex]\vec{F} = m \vec{a}[/latex]
In sorting data we can use something like the following.
-
- [latex]a =[/latex] accelerated motion
- [latex]v_i =[/latex]
- [latex]v_f =[/latex]
- [latex]d =[/latex]
- [latex]t =[/latex]
- [latex]F =[/latex] for unbalanced forces
- [latex]m =[/latex]
- [latex]a =[/latex]
In solving these problems one often encounters situations where the measure of acceleration is shared between the kinematic equations and Newton’s second law equation. This means that you might need to find the acceleration from Newton’s second law to use in a kinematic equation, or the reverse.
Also, it is common to encounter an increase in the number of conversions required to solve these problems, specifically speed, such as km/h to SI metric m/s, acceleration in gs to its equivalent in m/s2, and in being given the object’s weight, which you then need to convert to a mass in kg.
One unique feature of Newton’s second law is that you will encounter various forms of it in other parts in your studies in physics. It is also used as a quick derivation for the equations fundamental to the next chapters covered: Impulse and Momentum.
Example 6.4.1
A 25 kg body experiencing an unbalanced force of 100 N accelerates from rest through a distance of 90 m. For what amount of time was the unbalanced force acting on the body?
Solution
We need to solve this in two parts.
First:
- Data:
- [latex]F = 100 \text{ N}[/latex]
- [latex]m = 25 \text{ mg}[/latex]
- [latex]a = \text{ Find first}[/latex]
- Solution:
- [latex]F = m a[/latex]
- [latex]100 = \text{ N } = (25 \text{ kg}) a[/latex]
- [latex]a = 100 \text{ N } \div 25 \text{ kg}[/latex]
- [latex]a = 4.0 \text{ m/s}^2[/latex]
Second:
- Data:
- [latex]a = 4.0 \text{ m/s}^2[/latex]
- [latex]v_i = 0 \text{ m/s}[/latex]
- [latex]v_f = \text{ Not mentioned}[/latex]
- [latex]d = 90 \text{ m}[/latex]
- [latex]t = \text{ Find}[/latex]
- Solution:
- [latex]d = v_i t + \frac{1}{2} a t^2[/latex]
- [latex]90 \text{ m } = (0 \text{ m/s}) t + \frac{1}{2} (4.0 \text{ m/s}^2)t^2[/latex]
- [latex]90 \text{ m } = (2.0 \text{ m/s}^2)t^2[/latex]
- [latex]t^2 = 90 \text{ m } \div 2.0 \text{ m/s}^2[/latex]
- [latex]t^2 = 45 \text{ s}^2[/latex]
- [latex]t = 6.71 \text{ s}[/latex] (≈ 6.7 s)
Example 6.4.2
An unbalanced force acts on a 10 kg object resting on a frictionless surface for 7.5 s. If after 7.5 s the object is traveling at 5.0 m/s from rest, what force acted on it?
Solution
We need to solve this in two parts.
First:
- Data:
- [latex]a = \text{ Find first}[/latex]
- [latex]v_i = 0 \text{ m/s}[/latex]
- [latex]v_f = 5.0 \text{ m/s}[/latex]
- [latex]d = \text{ Not mentioned}[/latex]
- [latex]t = 7.5 \text{ s}[/latex]
- Solution:
- [latex]v_f = v_i + a t[/latex]
- [latex]5.0 \text{ m/s } = 0 \text{ m/s } + a (7.5 \text{ s})[/latex]
- [latex]a = 5.0 \text{ m/s } \div 7.5 \text{ s}[/latex]
- [latex]a = 0.67 \text{ m/s}^2[/latex]
Second:
- Data:
- [latex]F = \text{ Find}[/latex]
- [latex]m = 10 \text{ kg}[/latex]
- [latex]a = 0.67 \text{ m/s}^2[/latex]
- Solution:
- [latex]F = m a[/latex]
- [latex]F = (10 \text{ mg})(0.67 \text{ m/s}^2)[/latex]
- [latex]F = 6.7 \text{ N}[/latex]
Example 6.4.3
A 32000 kg jet has a braking force of 150000 N. What minimum length of runway is needed to bring this jet to a full stop if it lands traveling at 175 km/h?
Solution
We need to solve this in two parts.
First:
- Data:
- [latex]F = - 150\;000 \text{ N}[/latex]
- [latex]m = 32\;000 \text{ kg}[/latex]
- [latex]a = \text{ Find first}[/latex]
- Solution:
- [latex]F = m a[/latex]
- [latex]- 150\;000 \text{ N } = (32\;000 \text{ kg}) a[/latex]
- [latex]a = -150\;000 \text{ N } \div 32\;000 \text{ kg}[/latex]
- [latex]a = - 4.69 \text{ m/s}^2[/latex]
Second:
- Data:
- [latex]a = - 4.69 \text{ m/s}^2[/latex]
- [latex]v_i = 48.6 \text{ m/s}[/latex]
- [latex]v_f = 0 \text{ m/s}[/latex]
- [latex]d = \text{ Find}[/latex]
- [latex]t = \text{ Not mentioned}[/latex]
- Solution:
- [latex]2 a d = v_f^2 - v_i^2[/latex]
- [latex]2(-4.69 \text{ m/s}^2) d = (0 \text{ m/s})^2 - (48.6 \text{ m/s})^2[/latex]
- [latex](-9.375 \text{ m/s}^2) d = -2362 \text{ m}^2\text{/s}^2[/latex]
- [latex]d = -2362 \text{ m}^2\text{/s }^2 \div -9.375 \text{ m/s}^2[/latex]
- [latex]d = 252 \text{ m}[/latex]
Exercise 6.4
- An unbalanced force of 85 N is applied to a 10 kg mass for 5.0 s. If this mass was originally at rest, what distance did it cover during those 5.0 s
- A 5.0 g bullet leaves the barrel of a gun (1.0 m long) with a speed of 500 m/s. What was the average force acting on the bullet?
- If a hockey puck (mass of 250 g) was accelerated from rest to a final speed of 56 m/s through a distance of 1.0 m, what unbalanced force acted on this puck? (The maximum puck speed at the NHL level is around 170 km/h or 47 m/s)
- A 1200 kg automobile is traveling at 100 km/h. What is the average braking force required to bring this automobile to a full stop in 100 m?
- A 10 kg body experiencing an unbalanced force of 50 N accelerates from rest through a distance of 85 m. For what amount of time was the unbalanced force acting on the body?
- An unbalanced force of 50 N is applied to a 10 kg object at rest on a frictionless surface for 7.5 s. At what speed would one expect this object to be traveling after 7.5 s?
- A 10 000 N race car has an engine that can exert an unbalanced force of 35 000 N. In what amount of time could this car race the quarter mile (400 m)?
- A 15 000 kg jet has a braking force of 75 000 N. What minimum length of runway is needed to bring this jet to a full stop if it lands traveling at 325 km/h?
6.5 Calculating the Mass of the Earth’s Atmosphere
Exercise 6.5
- Given that the Earth’s atmosphere exerts a force of 101 300 N on each square metre of the Earth’s surface, estimate the mass of the atmosphere.
Exercise Answers
6.2 Newton’s Second Law
- 7.2 kg
- 12.5 m/s2
- 0 N
- − 610 N
- 0.0010 N or 1.0 mN
- 4.2 m/s2
- 0.034 m/s2 or 3.4 cm/s2
- 960 m/s2
6.3 Weight & Mass
-
- 150 N
- 30 m/s2
-
- 5.0 m/s2
- 49 m/s2
-
- 538 N
- 541 N
- 76 kg
- 250 N
- 730 N in both cases
- 1.4 m/s2
- 0.49 m/s2
- 9960 N to 36200 N
6.4 Newton’s Second & Accelerated Motion
- 106 m
- 625 N
- 390 N
- − 4630 N
- 5.8 s
- 37.5 m/s
- 4.8 s
- 815 m
6.5 Calculating the Mass of the Earth’s Atmosphere
- 5.3 × 1018
- Chemists measure mass in grams (g) using the cgs system ↵
- Evidence indicates that as the planet continues to warm, we could soon experience Category 6 Hurricanes (proposed). These hurricanes would rival the forces observed in F-4 tornadoes that are capable of picking up small cars, trucks and launching them as projectiles. ↵

