5 Projectile Motion

Equations Introduced and Used in this Topic: (All equations are generally written and solved as vector and all variables are the same measures and units as Chapter 3)

All measures are separated into vertical and horizontal components and assume zero air resistance.

  • Vertical Data
    • [latex]\vec{a} = -9.80 \text{ m/s}^2[/latex]
    • [latex]\vec{v_i} =[/latex]
    • [latex]\vec{d} =[/latex]
    • [latex]\vec{t} =[/latex]
  • Horizontal Data
    • [latex]\vec{v} =[/latex]
    • [latex]\vec{d} =[/latex]
    • [latex]t =[/latex]

Where…

  • [latex]v[/latex] is average speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
  • [latex]\vec{v}[/latex] is average velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
  • [latex]v_i[/latex] is initial speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
  • [latex]\vec{v_i}[/latex]is initial velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
  • [latex]v_f[/latex] is final speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
  • [latex]\vec{v_f}[/latex] is final velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
  • [latex]d[/latex] is distance traveled, commonly measured in metres (m), kilometres (km)
  • [latex]\vec{d}[/latex] is change in displacement, commonly measured in metres (m), kilometres (km) and includes a direction
  • [latex]a[/latex] is acceleration (deceleration is negative), measured in metres per second squared (m/s2)
  • [latex]\vec{a}[/latex] is vector acceleration, measured in metres per second squared (m/s2) and includes a direction
  • [latex]t[/latex] is Time, commonly measured in seconds (s) or hours (h)
 
Equations a vt  vi d t
[latex]v_t = v_i+ at[/latex] Not mentioned
[latex]2_{ad} = v_{r}^{2} - v_{i}^{2}[/latex] Not mentioned
[latex]d = v_{i}t + \dfrac{1}{2} at^2[/latex] Not mentioned
[latex]d = \dfrac{(v_i + v_t)t}{2}[/latex] Not mentioned

5.1 Horizontally Launched Projectiles

All measures are separated into vertical and horizontal components.

  • Vertical Data
    • [latex]\vec{a} = -9.80 \text{ m/s}^2[/latex]
    • [latex]\vec{v_i} =[/latex]
    • [latex]\vec{d} =[/latex]
    • [latex]\vec{t} =[/latex]
  • Horizontal Data
    • [latex]\vec{v} =[/latex]
    • [latex]\vec{d} =[/latex]
    • [latex]t =[/latex]

The reason for breaking all data into vertical and horizontal components is that gravity acts vertically and as such, only affects the vertical motion. The horizontal motion remains constant until the point that air resistance begins to affect both the vertical and horizontal motion. At this point, the physics that we use in algebra breaks down for the analysis of projectiles.

Historically, the study of projectiles was one of the first to gain importance due to its relevance in warfare, where the range and destructiveness of cannons being one of the projectiles studied. Until early researchers were able to break projectile motion into air resistance affected and non-affected, the narratives used were rather creative. The most common theory prior to accounting for air resistance was from the Theory of Impetus[1].

Impetus Theory underpinned the understanding of projectiles from its originator John Philoponus  and Avicenna in 6 CE, adopted and expanded my Nur ad-Din al-Bitruji at the end of the 12th century and adopted into Western scientific thought by Jean Buridan in the 14th century.

“When a mover sets a body in motion he implants into it a certain impetus, that is, a certain force enabling a body to move in the direction in which the mover starts it, be it upwards, downwards, sidewards, or in a circle. The implanted impetus increases in the same ratio as the velocity. It is because of this impetus that a stone moves on after the thrower has ceased moving it. But because of the resistance of the air (and also because of the gravity of the stone) which strives to move it in the opposite direction to the motion caused by the impetus, the latter will weaken all the time. Therefore the motion of the stone will be gradually slower, and finally the impetus is so diminished or destroyed that the gravity of the stone prevails and moves the stone towards its natural place. In my opinion one can accept this explanation because the other explanations prove to be false whereas all phenomena agree with this one.”

– Jean Buridan 14th Century

Eventually the Theory of Impetus was further refined into the concept of inertia by Galileo and was later quantified by Isaac Newton in his three laws of forces (chapter 6). This law of inertia simply states that an object in motion or a state of rest remains in that exact state of motion or state of rest unless an unbalanced force acts upon it.

In applying this to the analysis of projectiles:

  • Vertical Motion is constantly affected by the Earth’s Gravity resulting in the vertical motion to be constantly accelerated at 9.80 m/s2 downward near the Earth’s surface.
  • Horizontal Motion remains constant since the Earth’s Gravity only affects any motion up or down, not horizontally.

This means that in analyzing projectile motion, the motion must be broken up into vertical and horizontal components. The vertical part of the projectiles motion will be constantly accelerated by gravity (solved by the four kinematic equations) and the horizontal part will remain at a constant horizontal velocity (solved by the constant velocity equation).

  • Four Kinematic Equations:
    • [latex]d = \dfrac{(v_i + v_f) t}{2}[/latex]
    • [latex]2ad = v_f^2 - v_i^2[/latex]
    • [latex]\vec{v_f} = \vec{v_i} + \vec{a}t[/latex]
    • [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
  • Constant Velocity Equation
    • [latex]\vec{v} = \dfrac{\vec{d}}{t}[/latex]

The choice of equation to use can still be solved by using the chart introduced in Chapter 3.

Example 5.1.1

In a movie, a stunt-driver is to drive a car over a 4.0 m vertical drop traveling at 60 km/h. 

  1. At what velocity (vertical and horizontal) does this car strike the ground?
  2. What speed would this be?

Solution

Data:

Vertical Data Horizontal Data
[latex]\vec{a} = - 9.80 \text{ m/s}^2[/latex] [latex]\vec{v} = 60 \text{ km/h or } 16.7 \text{ m/s } (\approx 17 \text{ m/s})[/latex]
[latex]\vec{v_i} = 0 \text{ m/s}[/latex]
[latex]\vec{v_f} = \text{ Find}[/latex]
[latex]\vec{d} = - 4.0 \text{ m}[/latex]
[latex]t = \text{ Not mentioned}[/latex]

Question (i):

  • Horizontal velocity remains constant
  • [latex]2 \vec{a}\vec{d} = \vec{v_r}^2 - \vec{v_i}^2[/latex]
  • [latex]2(-9.80 \text{ m/s}^2)(-4.0 \text{ m}) = \vec{v_f}^2 - 0 \text{ m/s}[/latex]
  • [latex]78.4 \text{ m}^2\text{/s}^2 = \vec{v_f}^2[/latex]
  • [latex]\vec{v_f}^2 = 78.4 \text{ m}^2\text{/s}^2[/latex]
  • [latex]\vec{v_f} = \pm -8.85 \text{ m/s}[/latex]
  • Choose [latex]\vec{v_f} = -8.85 \text{ m/s } (\approx - 8.9 \text{ m/s})[/latex]

Question (ii):

To solve for the speed one must find the hypotenuse of these two velocity vectors. This is most easily done by using the Pythagorean Theorem: [latex]a^2 + b^2 = c^2[/latex]

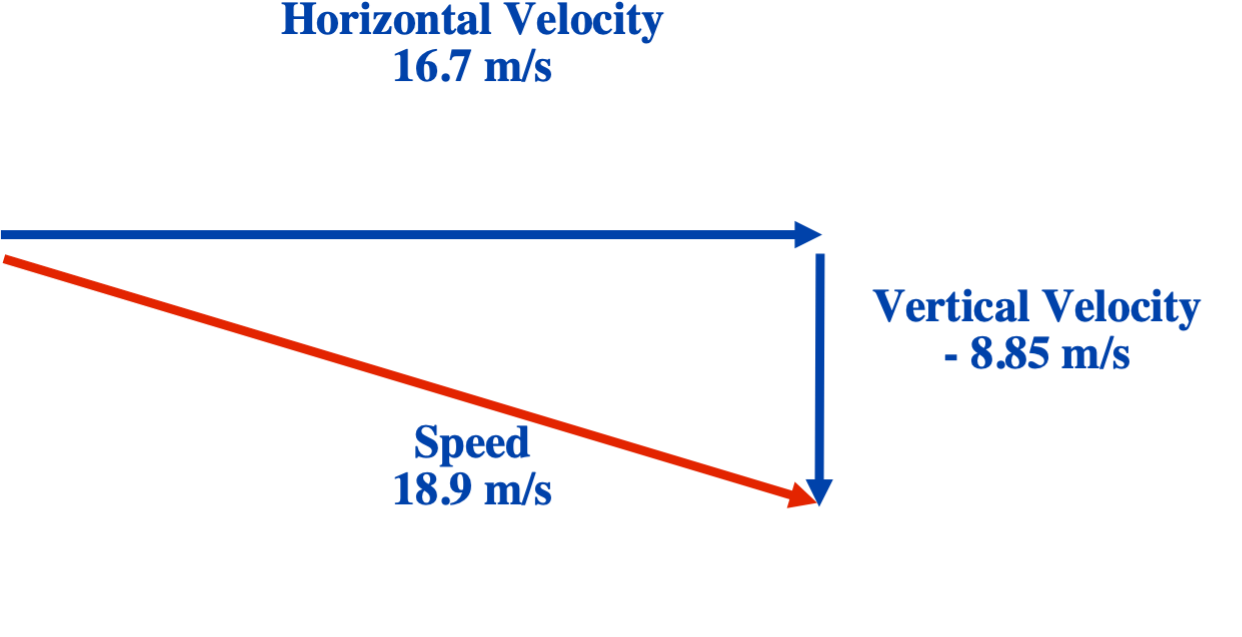
Therefore the speed is:

  • [latex]v^2 = (- 8.85 \text{ m/s})^2 + (16.7 \text{ m/s})^2[/latex]
  • [latex]v^2 = 78.4 \text{ m}^2\text{/s}^2 + 277.8 \text{ m}^2\text{/s}^2[/latex]
  • [latex]v^2 = 356.2 \text{ m}^2\text{/s}^2[/latex]
  • [latex]v = 18.9 \text{ m/s } (\approx 19 \text{ m/s})[/latex]
Extra Help: Horizontal and Vertical Velocity

Example 5.1.2

A marble rolls off a 1.5 m high bench with a velocity of 0.80 m/s. What horizontal distance does it travel before it strikes the floor?

Solution

Data:

Vertical Data Horizontal Data
[latex]\vec{a} = - 9.80 \text{ m/s}^2[/latex] [latex]\vec{v} = 0.80 \text{ m/s}[/latex]
[latex]\vec{v_i} = 0 \text{ m/s}[/latex] [latex]\vec{d} = \text{ Find second}[/latex]
[latex]\vec{v_f} = \text{ Not mentioned}[/latex] [latex]t = \text{ Use from Vertical Data}[/latex]
[latex]\vec{d} = - 1.5 \text{ m}[/latex]
[latex]t = \text{ Find first}[/latex]

First find the time in the air:

  • [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
  • [latex]-1.5 \text{ m } = (0 \text{ m/s})(t) + \frac{1}{2}(-9.80 \text{ m/s}^2)(t)^2[/latex]
  • [latex]-1.5 \text{ m } = (-4.9 \text{ m/s}^2)(t)^2[/latex]
  • [latex](t)^2 = -1.5 \text{ m } \div -4.9 \text{ m/s}^2[/latex]
  • [latex]t^2 = 0.306 \text{ s}^2[/latex]
  • [latex]t = 0.55 \text{ s}[/latex]

Second find the horizontal distance the marble travels:

  • [latex]v = \dfrac{d}{t}[/latex]
  • [latex]0.80 \text{ m/s} = \dfrac{d}{0.55 \text{ s}}[/latex]
  • [latex]d = (0.80 \text{ m/s})(0.55 \text{ s})[/latex]
  • [latex]d = 0.44 \text{ m}[/latex]

Example 5.1.3

A rock is thrown horizontally from a cliff with a velocity of 20 m/s.  What is the vertical and horizontal displacement8 of this rock after 3.0 s?

Solution

Data:

Vertical Data Horizontal Data
[latex]\vec{a} = - 9.80 \text{ m/s}^2[/latex] [latex]\vec{v} = 20 \text{ m/s}[/latex]
[latex]\vec{v_i} = 0 \text{ m/s}[/latex] [latex]\vec{d} = \text{ Find}[/latex]
[latex]\vec{v_f} = \text{ Not mentioned}[/latex] [latex]t = 3.0 \text{ s}[/latex]
[latex]\vec{d} = \text{ Find}[/latex]
[latex]t = 3.0 \text{ s}[/latex]

First find the vertical displacement:

  • [latex]\vec{d} = \vec{v_i}t + \frac{1}{2}\vec{a}t^2[/latex]
  • [latex]\vec{d} = (0 \text{ m/s})(t) + \frac{1}{2}(-9.80 \text{ m/s}^2)(3.0)^2[/latex]
  • [latex]\vec{d} = (-4.9 \text{ m/s}^2)(9.0 \text{ s}^2)[/latex]
  • [latex]\vec{d} = -44.1 \text{ m}(-44 \text{})[/latex]

Second find the horizontal displacement:

  • [latex]\vec{v} = \dfrac{\vec{d}}{t}[/latex]
  • [latex]\vec{d} = (20 \text{ m/s})(3.0 \text{ s})[/latex]
  • [latex]\vec{d} = 60 \text{ m}[/latex]

The total displacement change of the rock in those 3.0 s is:

[latex]\vec{d}[/latex] = − 44 m vertical and 60 m horizontal

The distance traveled would be found by using the Pythagorean Theorem from this data.

5.1 Horizontally Launched Projectiles

  1. A rock is thrown horizontally from a bridge.  By the time it strikes the water 44.1 m below, the rock has traveled a horizontal displacement of 15.0 m.  With what horizontal velocity was this rock thrown?
  2. A sea rescue airplane flying at 120 km/h and 45 m above water discovers shipwrecked people floating in a group. At what amount of time before they fly over the people should the aircraft drop emergency supplies?
  3. A diver running 3.5 m/s dives from the edge of a vertical cliff and reaches the water below 1.5 s later. How high was the cliff and how far from its base did this diver hit the water?
  4. A water balloon is thrown out of a window (10.0 m above ground) with a horizontal velocity of 6.0 m/s. Will the balloon hit a sunbather tanning on the ground that is 12 m away from the base of the window?
  5. A sack of flour is dropped from an airplane traveling at 125 m/s horizontally when 490 m above ground. How far forwards from the spot over which it dropped does the sack land? (Ignore air resistance)
  6. A car drives over a 20 m vertical drop traveling at 75 km/h. At what velocity (vertical and horizontal) does this car strike the ground?
  7. A UN airplane on a rescue mission into hostile territory has a horizontal velocity of 500 km/h and drops a supply package at an altitude of 1500 m. If the chute fails to open and air resistance does not affect the motion,
    1. in what amount of time would this package impact the ground?
    2. What horizontal distance would this package have traveled?
    3. What would be the packages impact speed?  (Ignore air resistance)
  8. A stone is thrown horizontally from a cliff with a velocity of 12 m/s.
    1. What is the stones vertical displacement after 1.0 s?
    2. What is the stones vertical displacement after 2.0 s?

  1. A cannon fires a cannonball with a velocity of 200 m/s with its barrel horizontal at a height of 1.2 m above the ground.
    1. How long would the cannon ball remain airborne before impacting the ground?
    2. What is the vertical & horizontal displacement of the cannonball when it strikes the ground?
    3. Which answers above, change if the launch velocity was reduced to 150 m/s?
  2. A pea is rolled off a table 1.0 m high with a velocity of 1.2 m/s. With what speed does this pea strike the floor?
  3. Back in the early 1970’s a bush plane pilot started to bomb a small town in a Northern Alberta with 5 pound bags of flour. He dropped about a dozen bags, managed to flatten one outhouse, dusting a couple of cars but no people.  He was arrested upon landing.  If he was flying at 120 km/h (horizontally) at a height of 50 m, what horizontal distance in front of his intended target should he have dropped his “bomb”?

5.2 Projectiles Launched at an Angle

All measures are broken up into vertical and horizontal components generally using right angled trigonometry where:

Basic Trigonometric Ratios

Trigonometric Defined Sides:

  • [latex]\sin= \dfrac{\text{Opposite}}{\text{Hypotenuse}}[/latex]
  • [latex]\cos = \dfrac{\text{Adjacent}}{\text{Hypotenuse}}[/latex]
  • [latex]\tan = \dfrac{\text{Opposite}}{\text{Adjacent}}[/latex]

As before, the choice of equation to use can be solved by using the chart introduced in chapter 3.

 
Equations a vt  vi d t
[latex]v_t = v_i+ at[/latex] Not mentioned
[latex]2_{ad} = v_{r}^{2} - v_{i}^{2}[/latex] Not mentioned
[latex]d = v_{i}t + \dfrac{1}{2} at^2[/latex] Not mentioned
[latex]d = \dfrac{(v_i + v_t)t}{2}[/latex] Not mentioned

Example 5.2.1

Suppose a baseball is hit and leaves the bat at 145 km/h at an angle of 30° above the horizontal.  In the absence of air resistance, what horizontal displacement would it travel before falling back to the height that it was struck?

Solution

First, you need to find the baseball’s vertical and horizontal components at launch.

Vertical:

  • Data:
    • ø = 30°
    • Launch Velocity = 145 km/h or 40.3 m/s
    • Vertical Velocity = Find
  • Trigonometry relationship to use is the sine function:
    • [latex]\sin 30^{\circ}=\dfrac{\text{Vertical velocity}}{40.3 \text{ m/s}}[/latex]
    • [latex]\text{Vertical velocity } = (40.3 \text{ m/s})(\sin 30^{\circ})[/latex]
    • [latex]\text{Vertical velocity } = 20.2 \text{ m/s}[/latex]

Horizontal:

  • Data:
    • ø = 30°
    • Launch velocity = 145 km/h or 40.3 m/s
    • Horizontal velocity = Find
  • Trigonometry relationship to use is the cosine function:
    • [latex]\cos 30^{\circ}=\dfrac{\text{Horizontal velocity}}{40.3 \text{ m/s}}[/latex]
    • [latex]\text{Horizontal velocity } = (40.3 \text{ m/s})(\cos 30^{\circ})[/latex]
    • [latex]\text{Horizontal velocity } = 34.9 \text{ m/s}[/latex]

This data is now put into the following chart:

Vertical Data Horizontal Data
[latex]\vec{a} = - 9.80 \text{ m/s}^2[/latex] [latex]\vec{v} = 34.9 \text{ m/s}[/latex]
[latex]\vec{v_i} = 20.2 \text{ m/s}[/latex] [latex]\vec{d} = \text{ Find}[/latex]
[latex]\vec{v_f} = -20.2 \text{ m/s}[/latex] [latex]t = \text{ Use from Vertical Data}[/latex]
[latex]\vec{d} = \text{ Not mentioned}[/latex]
[latex]t = \text{ Find first}[/latex]

First we use symmetry to sort out the data. If the baseball is launched at 20.2 m/s vertical then it should return to the same height at 20.2 m/s in the opposite direction as long as air resistance can be ignored.

Using the vertical data, the equation to be used is:

[latex]\vec{v_f} = \vec{v_i} + \vec{a}t[/latex]

Therefore:

  • [latex]- 20.2 \text{ m/s } = 20.2 \text{ m/s } + (- 9.80 \text{ m/s}^2)t[/latex]
  • [latex](-9.80 \text{ m/s}^2) t = - 20.2 \text{ m/s } - 20.2 \text{ m/s}[/latex]
  • Leaving [latex]t = \dfrac{- 40.4 \text{ m/s}}{- 9.80 \text{ m/s}2} \text{ or } 4.12 \text{ s}[/latex]

We now use this 4.12 s to find out how far the baseball traveled before it returned to the height at which it was struck.

Using the horizontal data, the equation to be used is:

[latex]\vec{v} = \dfrac{\vec{d}}{t}[/latex]

Therefore:

  • [latex]34.9 \text{ m/s } = \dfrac{\text{horizontal displacement}}{4.12 \text{ s}}[/latex]
  • [latex]\text{Leaving the horizontal displacement } = (34.9 \text{ m/s})(4.12 \text{ s})\text{ or } 144 \text{ m}[/latex]

In reality this 144 m will be affected by air resistance and other factors.

Exercise 5.2

  1. A cannonball is launched at 120 m/s at an angle of 35° above the horizontal.

    1. What are the initial vertical and horizontal launch velocities?
    2. What is the maximum vertical displacement reached?
    3. What amount of time will it take the cannonball to return to its launch height?
    4. What horizontal displacement will it have traveled when it has returned to its launch height?
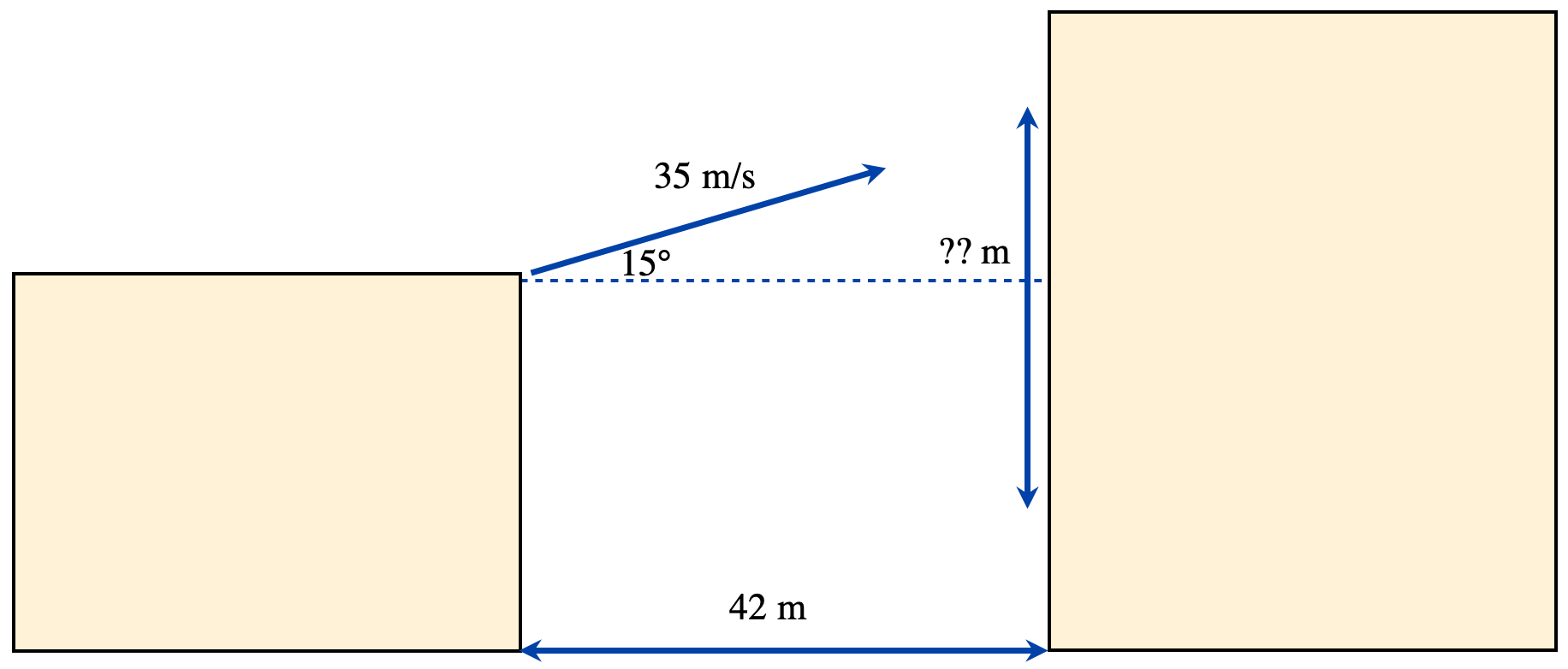
  2. Captain Ed, in training new recruits is directing a firehose at an angle of 15° above the horizontal from the roof of one building to a different building 42 m away. If the water is leaving the hose at 35 m/s, where will the water be striking the other building?

Exercise Answers

5.1 Horizontally Launched Projectiles

  1. 5.0 m/s
  2. 3.0 s
  3. 5.3 m (horizontal), −11 m (vertical)
  4. The balloon misses the sunbather
  5. 1250 m (No air resistance)
  6. 21 m/s (horizontal), −20 m/s (vertical)
    1. 17.5 s
    2. 2430 m
    3. 221 m/s
    1. −4.9 m
    2. −19.6 m
    1. 0.49 s
    2. 99 m (horizontal), −1.2 m (vertical)
    3. Yes. Time is unchanged, displacement is 74 m (horizontal) and −1.2 m (vertical)
  10. 4.6 m/s
  11. 106 m

5.2 Projectiles Launched at an Angle

    1. 68.8 m/s (vertical),
      98.3 m/s (horizontal)
    2. 241 m
    3. 140.s
    4. 1380 m
  2. 4.1 m up from launch height

Media Attributions

  1. Wikipedia: Theory of Impetus ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Foundations of Physics Copyright © by Terrance Berg is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book