13 Friction and Accelerated Motion
Resources
- Extra Help: Types of Forces
Equations Introduced and Used for this Topic:
- [latex]a=\dfrac{\Delta v}{t}[/latex]
- [latex]\vec{a}=\dfrac{\Delta \vec{v}}{t}[/latex]
- [latex]\Delta v=v_f-v_i[/latex]
- [latex]v=\dfrac{(v_1+v_f)}{2}[/latex]
- [latex]v_f=v_i+at[/latex]
- [latex]2ad={v_f}^2-{v_i}^2[/latex]
- [latex]d=v_it+\dfrac{1}{2}at^2[/latex]
- [latex]d=\dfrac{(v_i+v_f)t}{2}[/latex]
- [latex]F_f=\mu N \text{ or }\mu mg[/latex] (simplest case on horizontal surface)
- [latex]F_f=\mu N \text{ where }N=mg\text{ cos ø}[/latex] (on an inclined surface)
- [latex]F_{fs}=\mu _sN[/latex]
- [latex]F_{fk}=µ_kN[/latex]
- [latex]F_{fr}=µ_rN[/latex]
- [latex]F=ma[/latex]
- [latex]w=mg[/latex]
| Equations | [latex]a[/latex] | [latex]{v_f}^2[/latex] | [latex]{v_i}^2[/latex] | [latex]d[/latex] | [latex]t[/latex] |
|---|---|---|---|---|---|
| [latex]v_f=v_i+at[/latex] | Not Mentioned | ||||
| [latex]2ad={v_f}^2-{v_i}^2[/latex] | Not Mentioned | ||||
| [latex]d=v_it+\dfrac{1}{2}at^2[/latex] | Not Mentioned | ||||
| [latex]d=\dfrac{(v_i+v_f)t}{2}[/latex] | Not Mentioned |
Where…
- [latex]F[/latex] is Force, measured in newtons (N)
- [latex]w[/latex] is Weight (it is a Force), measured in newtons (N)
- [latex]m[/latex] is Mass, commonly measured in kilograms (Kg), grams (g) or tonnes (t)
- [latex]a[/latex] is Acceleration (deceleration is negative), measured in metres per second squared (m/s2)
- [latex]g[/latex] or [latex]a_g[/latex] is the Acceleration due to Gravity and varies from 9.78 m/s2 (equator) to 9.83 m/s2 (North or South poles) … The average value of gravity is taken to be either 9.80 m/s2 or 9.81 m/s2
- [latex]F_f[/latex] is the Force of Friction, measured in newtons (N)
- [latex]µ_s, µ_k\text{ & }µ_r[/latex] are Coefficients of Friction and are magnitudes without units
- [latex]N[/latex] is the Normal Force, measured in newtons (N)
- [latex]F_{fs}[/latex] is the Force of Static Friction, measured in newtons (N)
- [latex]F_{fk}[/latex] is the Force of Kinetic Friction, measured in newtons (N)
- [latex]F_{fr}[/latex] is the Force of Rolling Friction, measured in newtons (N)
- ø is the measure of the Incline of the Surface the object is resting on
And…
- [latex]v[/latex] is Speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
- [latex]\vec{v}[/latex] is Velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
- [latex]v_i[/latex] is Initial Speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
- [latex]\vec{v_i}[/latex] is Initial Velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
- [latex]v_f[/latex] is Final Speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
- [latex]\vec{v_f}[/latex] is Final Velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
- [latex]∆ d[/latex] is Distance travelled, commonly measured in metres (m), kilometres (km)
- [latex]\Delta \vec{d}[/latex] is Change in Displacement, commonly measured in metres (m), kilometres (km)
and includes a direction - [latex]a[/latex] is Acceleration (deceleration is negative), measured in metres per second squared (m/s2)
- [latex]\vec{a}[/latex] is Vector Acceleration, measured in metres per second squared (m/s2) and includes a direction
- [latex]t[/latex] is time, commonly measured in seconds (s) or hours (h)
| Materials | Surface conditions | μk |
|---|---|---|
| Glass on glass | clean | 0.90 – 1.0 |
| Wood on wood | clean and dry | 0.25 – 0.5 |
| Wood on wood | wet | 0.2 |
| Steel on steel | clean | 0.58 |
| Steel on steel | motor oil lubricant | 0.2 |
| Rubber on solids | dry | 1 – 4 |
| Teflon on steel | clean | 0.04 |
| Waxed hickory on dry snow | 0.03 – 0.06 | |
| Brass on ice | 0.02 – 0.08 |
13.1 Friction
- Article to Read: Leonardo da Vinci – The systemic study of friction
- Extra Help: Types of Forces
Equations Introduced or Used for this Section:
- [latex]F_{fs}=\mu _sN[/latex]
- [latex]F_{fk}=µ_kN[/latex]
- [latex]F_{fr}=µ_rN[/latex]
- [latex]F=ma[/latex]
- [latex]w=mg[/latex]
The by product of friction is generally heat.

Friction is a resistive force that acts to oppose the relative motion between two surfaces (objects, fluids, gases) that are moving past one another or are attempting to move. Studies of friction find their origin in various Greek philosophers as Aristotle (384-322 BCE), Victruvius (80 or 70 BCE- 15 BCE) and Pliny the Elder (23-79 CE), who were interested in both the causes of friction and how to reduce the amount of friction. The difference in frictional types of static and kinetic was known as early as Themistus (317-390 CE) who stated “it is easier to further the motion of a moving body than to move a body at rest“.

The first to develop the classic laws of friction was Leonardo da Vinci (1452-1519), who recorded his investigations using sketches of sliding blocks (shown above) on inclined surfaces. His ideas to use sliding blocks are still used today in demonstrating the fundamentals of friction that exists between solid bodies. Da Vinci’s works were never published and remained unknown until over 150 years later they were discovered again by Guillaume Amontons (1663-1705) and published as the Laws of Static Friction:
- 1st Law: The force of friction is directly proportional to the applied load.
- 2nd Law: The force of friction is independent of the apparent area of contact.
- 3rd Law: Kinetic friction is independent of the sliding velocity.
Amonton’s laws can be demonstrated by objects such as a brick resting on an inclined plane. Expanding the concept of friction from static to kinetic was accomplished by Bernard Forest de Bélidor (1698-1761) and Leonhard Euler (1707-1783). Charles-Augustin de Coulomb (1736-1806) established that friction depended on several factors, such as the nature of the materials and coatings of the surfaces in contact, the weight or force of the load on the surface (Normal Force) and the length of time these surfaces were to remain in contact. The classical model of friction was completed by Arthur Morin (1795-1880) in his work on differences between sliding and rolling frictions, and that of Osborne Reynolds (1842-1912), who added the concept of friction that exists in the flow of fluids.
Current research is exploring the role of friction in earthquakes, in artificial limbs and hip replacements, tiny sensors that control air bags, nanotech investigations of polymer molecules to create fluids to reduce friction, and even exploring the role of rupture waves similar to sound waves in altering friction depending on the direction of motion. Some of the main motivations for this and other work are to increase the longevity and to reduce energy loss as we become more aware of the importance in not losing energy in devices. Studies of friction are of importance.
In this section, we will quantify static, kinetic and rolling frictions. The equations for these follow a pattern, that of the frictional force being a coefficient given by a standard symbol µ (value or ratio) of the Normal Force. The equations for all three of these frictions are shown below.
- [latex]F_{fs}=\mu _sN[/latex]
- [latex]F_{fk}=µ_kN[/latex]
- [latex]F_{fr}=µ_rN[/latex]
In all cases the symbol for friction is given by Ff with a subscript to distinguish which type of friction it is: s for static, k for kinetic and r for rolling.
The Normal Force is often described as the support force of a surface or other stable object that is in contact with an object being supported. For an object on a desk or a chair, the Normal Force is the supporting force that acts to balance whatever force (generally gravity) that is holding the object to the surface. If a person pushes a book against a wall, then the Normal Force will be balancing this force.
Finding the coefficients of friction between two bodies is a complicated activity, since it is an attempt to quantify the relationship between the Frictional Force and the Normal Force. Technically, it is done through multiple experiments of two objects under similar conditions that can be affected by temperature, humidity, air pressure, dust, the types of solids, whether any fluids are present between the two surfaces, if the surfaces are flat and uniform … This list goes on. In theory, the coefficient of friction also takes into account both mechanical interactions and actions at the atomic level.
The following examples explore introductory friction questions on a flat horizontal surface.
Example 13.1.1
A 120 kg refrigerator rests on the floor. What applied force is required to move this refrigerator if [latex]µ_s[/latex] = 0.15 exists between the refrigerator and the floor?
Solution
We need an applied force that is greater than the static frictional force.
- [latex]F_{\text{applied}}[/latex] > [latex]F_{fs}[/latex] (or [latex]µ_s N[/latex])
- [latex]F_{\text{applied}}[/latex] > (0.15)(120 kg)(9.8 m/s2) cos 0°
- [latex]F_{\text{applied}}[/latex] > 196 N (≈ 180 N)
Example 13.1.2
An applied force of 420 N is needed to maintain the constant velocity of a 1200 kg car rolling along the street. What is the [latex]µ_r[/latex] acting between this car and the road?
Solution
We need an applied force that equals the rolling frictional force.
- [latex]F_{\text{applied}}[/latex] > [latex]F_{fr}[/latex] (or [latex]µ_r N[/latex])
- 420 N = ([latex]µ_r[/latex])(1200 kg)(9.8 m/s2) cos 0°
- [latex]µ_r[/latex] = 420 N ÷ 11760 N
- [latex]µ_r[/latex] = 0.036
Example 13.1.3
An applied force of 280 N is just enough to push a crate at a constant velocity on ice (mass of 140 kg). What is [latex]µ_k[/latex] between this crate and the ice?
Solution
We need an applied force that equals the kinetic frictional force
- [latex]F_{\text{applied}}[/latex] > [latex]F_{fk}[/latex] (or [latex]µ_k N[/latex])
- 280 N = (µ_k)(140 kg)(9.8 m/s2) cos 0°
- [latex]µ_k[/latex] = 280 N ÷ 1372 N
- [latex]µ_k[/latex] = 0.204
Exercise 13.1
- A 40 kg wooden crate rests on the floor. What applied force is required to set this crate in motion if µs = 0.50 exists between the crate and the floor?
- An applied force of 300 N is needed to maintain the constant velocity of a 100 kg crate sliding across a warehouse floor. What is the µk acting between this crate and the floor
- An applied force of 200 N is just enough to start a motorcyclist and her bike rolling (combined mass of 500 kg). What is the µr between this bike & rider and the road?
- A truck that has a weight of 15000 N is parked on a level road. If µs = 0.48 what is the maximum frictional force with which this truck would resist an applied force?
- A person is pulling a 25 kg sled horizontally. If the µk is 0.08, what horizontally applied force is needed to keep this sled moving at an average speed?
- The engine of a 1200 kg car can accelerate with an unbalanced force of 10000 N. What must be the minimum µs to prevent this car from spinning its tires?
13.2 Friction & Newton’s Second Law
Equations Introduced or Used for this Section:
- [latex]F_f=\mu N\text{ or “}\mu mg\text{" (simplest case)}[/latex]
- [latex]F_f=\mu N\text{ where }N=mg\text{ cos ø}[/latex]
- [latex]F_{fs}=\mu _sN[/latex]
- [latex]F_{fk}=µ_kN[/latex]
- [latex]F_{fr}=µ_rN[/latex]
- [latex]F=ma[/latex]
- [latex]w=mg[/latex]
In this section of questions we explore the relationship between Net Force, Applied Force, Frictional Forces and Newton’s second law. Central to this is the concept that friction resists the vector sum of applied forces, and if there is an unbalanced force (Net Force) that results from the blend of applied forces and friction, then acceleration results. Quantified, this relationship looks as follows:
[latex]F_\text{net}=F_\text{applied}-F_f\text{ where }F_\text{net}=ma[/latex]
The results of these calculations mean:
For an object at rest:
- If [latex]F_\text{net}=0[/latex], then [latex]F_\text{applied}=F_f[/latex]
For an object in motion:
- If [latex]F_\text{net}>0[/latex], then [latex]F_\text{net}=ma[/latex] and the object or system is accelerating.
- If [latex]F_\text{net}<0[/latex], then [latex]F_\text{net}=ma[/latex] and the object or system is decelerating or remains in a static situation.
One feature of interest is the role of friction in accelerating and decelerating. Friction will dictate the maximum value that some objects can accelerate or decelerate. An examples of this is the friction of tires on a road. The maximum rate of braking when decelerating depends on the friction that exists between the tires and the road. Likewise, the maximum rate that a vehicle can accelerate on a surface is dictated by the maximum friction that exists between the tires and the road. One can always add extra forces to complicate accelerating and decelerating but at the simplest:
acceleration & deceleration < maximum friction
If we are to summarize and put all the above on a sketch showing a change of applied force compared to friction as a function of time, then we would have something as follows.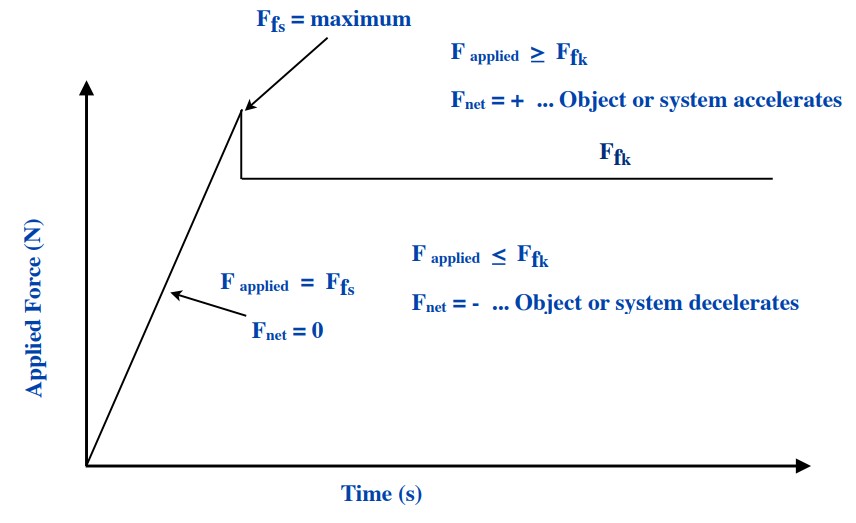
There are two distinct regions shown with five possibilities:
- If we are looking at how much force we are applying to an object at rest, the object will remain at rest until we are able to apply a force that is greater than the static force that resists it.
- When the [latex]F_\text{applied}= F_{fs}[/latex] and the object remains at rest or the [latex]F_\text{net} = 0[/latex]
- When the [latex]F_\text{applied} > F_{fs}[/latex] and the object will accelerate and the [latex]F_\text{net}= ma[/latex]
- If we are looking at how much force we are applying to an object in motion, the object will react differently depending on how the applied force compares to the frictional force.
- When the [latex]F_\text{applied}= F_{fs}[/latex] and the object remains at constant speed or the [latex]F_\text{net}=0[/latex]
- When the [latex]F_\text{applied}>F_{fs}[/latex] and the object will accelerate and the [latex]F_\text{net}=ma[/latex]
- When the [latex]F_\text{applied}< F_{fs}[/latex] and the object will decelerate and the [latex]F_\text{net}=ma[/latex]
Example 13.2.1
A force of 170 N is applied to a 85 kg stove resting on the floor.
- If this force is just enough to start it sliding, find µs.
Solution- [latex]F_\text{applied}= F_{fs}\text{ or }\mu_s mg\text{ cos ø}[/latex]
- 170 N = [latex]µ_s[/latex] (85 kg)(9.8 m/s2) cos 0°
- [latex]µ_s[/latex] = 170 N ÷ 833 N
- [latex]µ_s[/latex] = 0.204 (≈ 0.20)
- Find the acceleration of this stove (once moving) if [latex]µ_k[/latex] drops to 0.15 and a force of 100 N continues to be applied. (Or does it continue to accelerate?)
Solution- [latex]F_\text{net}=F_\text{applied} - F_{fk}[/latex]
- [latex]ma=100\text{ N}-\mu_k mg\text{ cos ø}[/latex]
- (85 kg) [latex]a[/latex] = 100 N − (0.15)(85 kg) (9.8 m/s2) cos 0°
- (85 kg) [latex]a[/latex] = 100 N − 125 N
- [latex]a[/latex] = − 25N ÷ 85 kg or − 0.29 m/s2
- The Applied Force is not larger than friction and the stove will decelerate to a stop.
Example 13.2.2
Suppose the grip of your car tires on clean pavement has a µs of 1.60. What is the maximum possible acceleration of your car using these tires?
Solution
- [latex]F_\text{net}=F_f\text{ where }F_\text{net}=ma\text{ and }F_{fs}=\mu _sN[/latex]
This means that:
- [latex]ma=\mu _sN[/latex] in this case [latex]N=mg\text{ cos ø}[/latex]
- [latex]ma=\mu _s mg\text{ cos ø}[/latex]
Cancel out the common mass and we are left with …
- [latex]a=\mu _s g\text{ cos ø}[/latex]
For horizontal surfaces we
- [latex]a[/latex] = (1.60)(9.80 m/s2) [latex]\cos[/latex]0°
- [latex]a[/latex] = 15.7 m/s2
Exercise 13.2
- Several people pushing together make a combined applied force of 1000 N on a 1200 kg car that has just started to roll. If µr is 0.04, find the resulting acceleration of this car.
- A force of 200 N is applied to a 50 kg crate resting on the floor.
- If this force is just enough to start it sliding, find µs.
- Find the acceleration of this crate (once moving) if µk drops to 0.30 and a force of 200 N continues to be applied.
- Some of the best tires have a µs of 4.0. What is the maximum possible acceleration of cars that use these tires?
13.3 Friction & Accelerated Motion
Equations Introduced or Used for this Section:
- [latex]a=\dfrac{\Delta v}{t}[/latex]
- [latex]\vec{a}=\dfrac{\Delta \vec{v}}{t}[/latex]
- [latex]\Delta v=v_f-v_i[/latex]
- [latex]v=\dfrac{(v_1+v_f)}{2}[/latex]
- [latex]v_f=v_i+at[/latex]
- [latex]2ad={v_f}^2-{v_i}^2[/latex]
- [latex]d=v_it+\dfrac{1}{2}at^2[/latex]
- [latex]d=\dfrac{(v_i+v_f)t}{2}[/latex]
- [latex]F_f=\mu N \text{ or }\mu mg[/latex] (simplest case on horizontal surface)
- [latex]F_f=\mu N \text{ where }N=mg\text{ cos ø}[/latex] (on an inclined surface)
- [latex]F_{fs}=\mu _sN[/latex]
- [latex]F_{fk}=µ_kN[/latex]
- [latex]F_{fr}=µ_rN[/latex]
- [latex]F=ma[/latex]
- [latex]w=mg[/latex]
| Equations | [latex]a[/latex] | [latex]{v_f}^2[/latex] | [latex]{v_i}^2[/latex] | [latex]d[/latex] | [latex]t[/latex] |
|---|---|---|---|---|---|
| [latex]v_f=v_i+at[/latex] | Not Mentioned | ||||
| [latex]2ad={v_f}^2-{v_i}^2[/latex] | Not Mentioned | ||||
| [latex]d=v_it+\dfrac{1}{2}at^2[/latex] | Not Mentioned | ||||
| [latex]d=\dfrac{(v_i+v_f)t}{2}[/latex] | Not Mentioned |
Example 13.3.1
What distance is needed to bring a 1500 kg truck (traveling at 90 km/h) to a full stop on a rainy day if the [latex]µ_s[/latex] between the tires and the wet road is 0.42?
Solution
The maximum deceleration is defined by the maximum static grip on the road. The frictional force in this problem is negative, since it is slowing the truck down to a stop.
Therefore:
- [latex]F_\text{Net}=-F_{fs}[/latex]
- [latex]ma=-\mu_s m g \cos ø[/latex]
Cancelling out the common mass:
- [latex]a=-\mu _s g \text{ cos ø}[/latex]
- [latex]a[/latex] = − (0.42)(9.80 m/s2) cos 0°
- [latex]a[/latex] = − 4.12 m/s2
Now:
- [latex]a[/latex] = − 4.12 m/s2
- [latex]v_i[/latex] = 90 km/h or 25 m/s
- [latex]v_f[/latex] = 0 m/s … stopped
- [latex]d[/latex] = Find
- [latex]t[/latex] = Not mentioned
Solution:
- Use [latex]2ad={v_f}^2-{v_i}^2[/latex]
- [latex]2 (- 4.12\text{ m/s}^2) d = (0\text{ m/s})^2-(25\text{ m/s})^2[/latex]
- [latex](-8.24\text{ m/s}^2)d=-625\text{ m}^2\text{/s}^2[/latex]
- [latex]d=dfrac{-625\text{ m}^2\text{/s}^2}{-8.24\text{ m/s}^2}[/latex]
- [latex]d[/latex] = 75.8 m
Example 13.3.2
A snowboarder traveling at 60 km/h slows to a speed of 5 km/h before stepping off the snowboard. If this snowboarder travels 20 m slowing down what was the average µk?
Solution
First:
Data:
- [latex]a[/latex] = Find
- [latex]v_i[/latex] = 60 km/h or 16.7 m/s
- [latex]v_f[/latex] = 5 km/h or 1.39 m/s
- [latex]d[/latex] = 20 m
- [latex]t[/latex] = not mentioned
Solution:
- Use [latex]2ad={v_f}^2-{v_i}^2[/latex]
- [latex]1a(20\text{ m})=(1.39\text{ m/s})^2-(16.7\text{ m/s})^2[/latex]
- [latex](40\text{ m})a=-277\text{ m}^2\text{/s}^2[/latex]
- [latex]a=\dfrac{-277\text{ m}^2\text{/s}^2}{40\text{m}}[/latex]
- [latex]a[/latex] = − 6.92 m/s2
Now…
- [latex]F_\text{Net}=-F_{fk}[/latex]
- [latex]ma=-\mu k mg\text{ cos ø}[/latex]
Cancelling out the common mass:
- [latex]a=-\mu _k g\text{ cos ø}[/latex]
- − 6.92 m/s2 = [latex]- \mu_k[/latex] (9.80 m/s2) cos 0°
- [latex]µ_k[/latex] = − 6.92 m/s2 ÷ − 9.80 m/s2
- [latex]µ_k[/latex] = 0.71 (≈ 0.7)
Example 13.3.3
A person is standing in the middle of an ice rink 12 m away from the boards. If the µs between this person’s feet and the ice is 0.080, what is the shortest amount of time this person would take to reach the boards?
Solution
First, we need to find the maximum acceleration from the grip on the ice that this person can achieve.
Therefore:
- [latex]F_\text{Net}=-F_{fs}[/latex]
- [latex]ma=-\mu s mg\text{ cos ø}[/latex]
Cancelling out the common mass:
- [latex]a=-\mu _s g\text{ cos ø}[/latex]
- [latex]a[/latex]= (0.08)(9.80 m/s2) cos 0°
- [latex]a[/latex] = 0.784 m/s2
Now:
- [latex]a[/latex] = 0.784 m/s2
- [latex]v_i[/latex] = 0 m/s
- [latex]v_f[/latex] = not mentioned
- [latex]d[/latex] = 12 m
- [latex]t[/latex] = Find
Solution:
- Use [latex]d=v_it+\dfrac{1}{2}at^2[/latex]
- [latex]12\text{ m}=(0\text{ m/s})t+\dfrac{1}{2}(0.784\text{ m/s}^2)t^2[/latex]
- [latex]12\text{ m}=(0.392\text{ m/s}^2)t^2[/latex]
- [latex]t^2=\dfrac{12\text{ m}}{0.392\text{ m/s}^2}[/latex]
- [latex]t[/latex] = 5.5 s
Exercise 13.3
- A hubcap leaves a moving car traveling at 40 km/h and rolls for 200 m before coming to a full stop. What is the average µr acting on this hubcap?
- What distance is needed to bring a 1200 kg car (traveling at 100 km/h) to a full stop if the µs between the tires and the road is 0.38?
- What distance would this car skid if the µk between its tires and the road is 0.26?
- A skier on wet snow experiences a µk of 0.10. What would be the maximum distance this skier would travel on level ground before stopping if he/she had an initial speed of 35 km/h?
- A water skier traveling at 50 km/h slows to a speed of 10 km/h before sinking under water. If this skier travels 50 m while slowing down what was the average µk?
- With a µk of 0.05, what distance will an ice skater traveling at 18 m/s glide before coming to a full stop?
- A snow skier traveling at 45 km/h slows to a stop over a horizontal distance of 350 m. What was the average µk?
- A person is standing in the middle of an ice rink 20 m away from the boards. If the µs between the persons shoe and ice is 0.04 what is the shortest amount of time this person would take to reach the boards?
- A 80 kg person is standing on ice, where the coefficients of friction between the person’s feet and the ice are µs = 0.06. If a 10 kg medicine ball is thrown to this person to catch at a speed of 4.0 m/s, is the person going to be able to stand still? (It takes 0.50 s for the person to bring this ball to a full stop)
- In a lawn bowling game, a 3.5 kg bowling ball is rolling at 4.2 m/s travels 18 m before coming to a stop. What is the average frictional force that is acting on the bowling ball?
13.4 Friction on an Inclined Surface
Equations Introduced or Used for this Section:
Basic Trigonometric Ratios
- [latex]\text{Sin}=\dfrac{\text{Opposite}}{\text{Hypotenuse}}[/latex]
- [latex]\text{cos}=\dfrac{\text{Adjacent}}{\text{Hypotenuse}}[/latex]
- [latex]\text{Tan}=\dfrac{\text{Opposite}}{\text{Adjacent}}[/latex]
[latex]F_f=\mu N \text{ where }N=mg\text{ cos ø}[/latex]
- [latex]F_{fs}=\mu _sN[/latex]
- [latex]F_{fk}=µ_kN[/latex]
- [latex]F_{fr}=µ_rN[/latex]
- [latex]F=ma[/latex]
- [latex]w=mg[/latex]
When we consider multiple forces acting on a body or a system we are drawing what is known as Free Body Diagrams. Free body diagrams represent a picture of the forces that are acting on a body or a system. In the examples below, the forces illustrated are friction, applied forces, the Normal force and weight.

You can see for these situations that the angle of the incline is 0° and as such cos 0° = 1. Because of this, introductory physics students often remember the Normal force as equaling [latex]N=mg[/latex] instead of the proper [latex]N=mg\text{ cos ø}[/latex], where the only force holding the object to the surface is gravity. This is a request for you as students to use the equation for Normal Force as given by the equation: [latex]N=mg\text{ cos ø}[/latex]
These diagrams become a little more complicated when used to analyze objects on inclined surfaces.
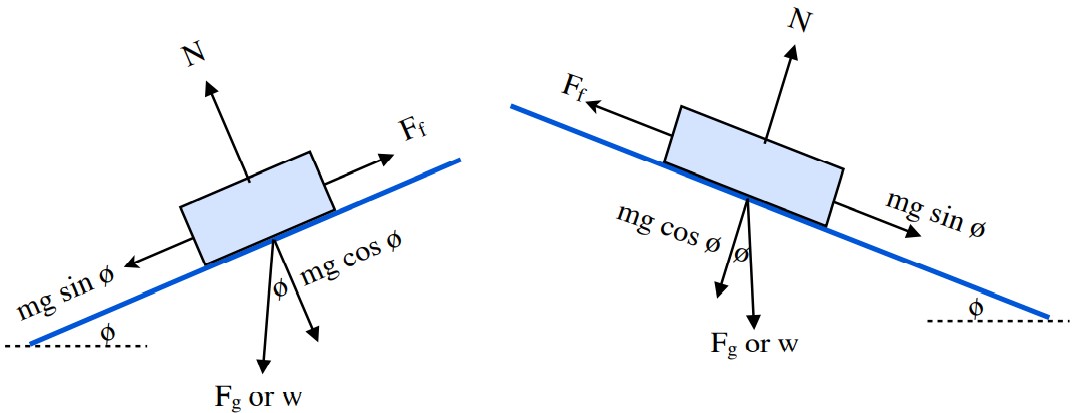
Both of these examples are nearly identical to the previous Free Body Diagrams, except that they now take the weight vector and break it up into the force that is pulling the object directly into the surface and the part of the force that is now acting to pull the object down the plane.
These Free Body diagrams can be also drawn showing Forces that act in either direction, both up and down the inclined surface. As above, the Free Body Diagrams are identical to the ones above with one addition, the applied force and the direction of the frictional force. The frictional force will always act opposite to the net force between applied force and the force of gravity pulling the object down the incline. In the example to the left, the frictional force is shown as acting either up or down the incline. Friction in this case acts opposite to the direction of the vector sum of the applied force and the force of gravity pulling down the incline.
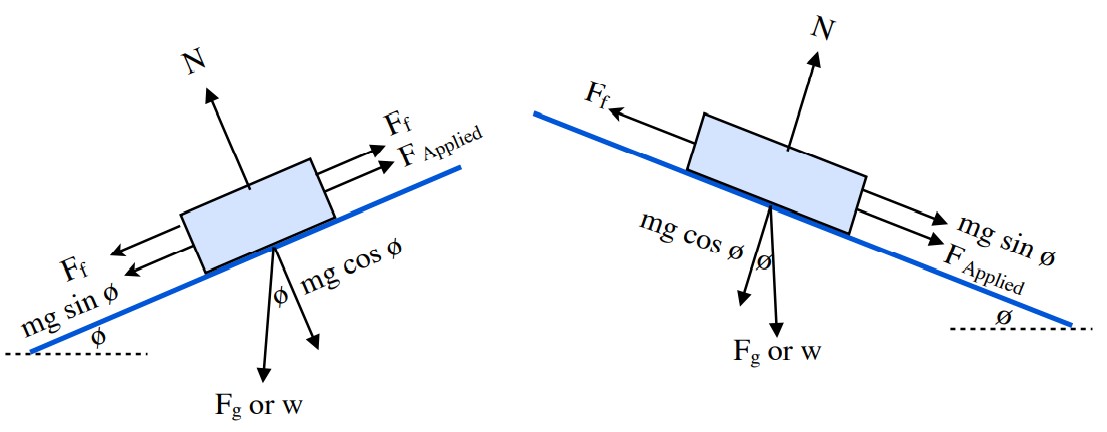
Example 13.4.1
Draw the Free Body diagram for the following questions using the data given.
 [latex]m[/latex] = 40 kg, [latex]F_{\text{Applied}}[/latex] = [latex]F_{fs}[/latex] = 20 N
[latex]m[/latex] = 40 kg, [latex]F_{\text{Applied}}[/latex] = [latex]F_{fs}[/latex] = 20 N
- [latex]N=mg\text{ cos ø}[/latex]
- N = (40 kg)(9.80 m/s2) cos 0°
- N = 392 N
- [latex]m[/latex] = 12 kg, [latex]F_{\text{Applied}}[/latex] = 20 N (left), [latex]F_f[/latex] = 8 N (right)
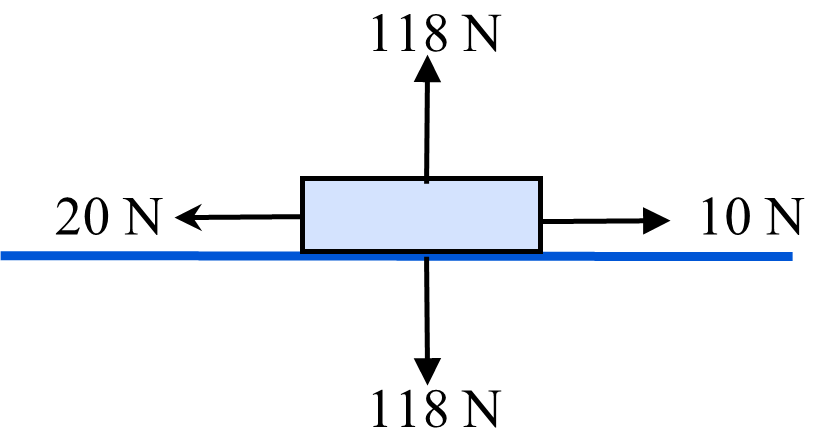
- [latex]N=mg\text{ cos ø}[/latex]
- [latex]N[/latex] = (12 kg)(9.80 m/s2) cos 0°
- [latex]N[/latex] = 118 N
- m = 8 kg, [latex]F_{\text{Applied}}[/latex] = 20 N (down), [latex]F_f[/latex]= 32 N (up), ø = 15°

- [latex]w=mg[/latex]
- [latex]w[/latex] = (8 kg)(9.80 m/s2)
- [latex]w[/latex] = 78.4 N
- [latex]N=m g \cos ø[/latex]
- [latex]N[/latex] = (8 kg)(9.80 m/s2) [latex]\cos[/latex] 15°
- [latex]F_d=mg\text{ cos ø}[/latex]
- [latex]F_d[/latex] = (8 kg)(9.80 m/s2) [latex]\sin[/latex] 15°
- [latex]F_d[/latex] = 20.3 N
Example 13.4.2
A truck is coasting downhill on a steep slope angled at 7°, maintaining a constant speed. If the coefficient of rolling friction is [latex]µ_r[/latex] = 0.07, and the truck and driver have a mass of 1750 kg, what is the average braking force that is needed?
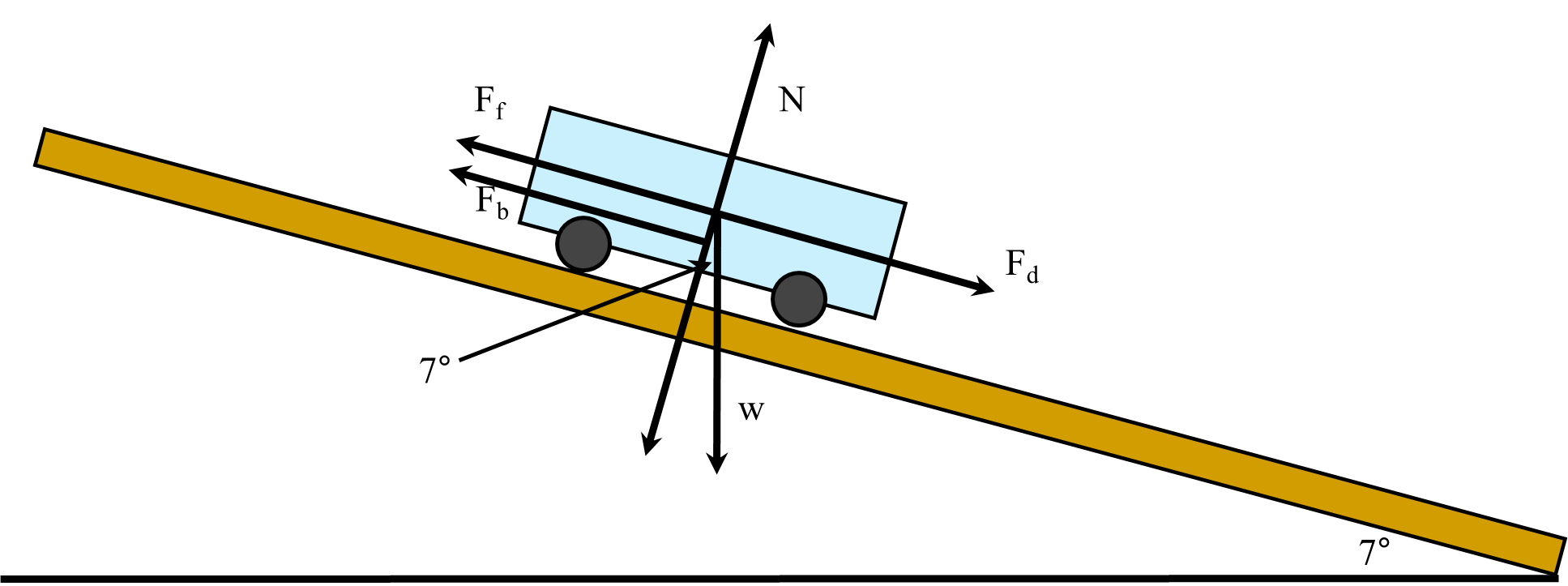
Solution
For this problem, the forces we need to work with are:
- [latex]F_d=mg\text{ sin ø}[/latex]
- [latex]F_{fr}=\mu_rN\text{ or }\mu_rmg\text{ cos ø}[/latex]
- and [latex]F_b=\text{ Find}[/latex]
Equating them yields:
- [latex]F_{fr}+F_b=F_d[/latex]
Which expands to …
- [latex]\mu_r m g \cos ø + F_b =mg\text{ sin ø}[/latex]
- (0.07)(1750 kg)( 9.80 m/s2) [latex]\cos[/latex] 7° + [latex]F_b[/latex] = (1750 kg) 9.80 m/s2) sin 7°
- 1192 N + [latex]F_b[/latex] = 2090 N
- [latex]F_b[/latex] = 2090 N − 1192 N
- [latex]F_b[/latex] = 898 N
Exercise 13.4
- A car is rolling downhill on a road angled at 6°. If the coefficient of rolling friction is [latex]µ_r[/latex] = 0.05, and the car and driver have a mass of 1450 kg, what is the average acceleration of the car and driver?
- A car is coasting downhill on a steep slope angled at 8°, maintaining a constant speed. If the coefficient of rolling friction is µr = 0.08, and the car and driver have a mass of 1350 kg, what is the average braking force that is needed?
- A block is at rest on a board that is being raised at one end. At a certain angle ø the block begins to slide. If the coefficient of static friction is [latex]µ_s[/latex] = 0.42, what is the angle ø at which the block begins to slide?
Exercise Answers
13.1 Friction
- ≥ 196 N
- 0.306
- 0.041
- ≤ 7200 N
- 19.6 N
- 0.85
13.2 Friction & Newton’s Second Law
- 0.44 m/s2
-
- 0.41
- 1.1 m/s2
- 39.2 m/s2
13.3 Friction & Accelerated Motion
- 0.031
- 104 m
- 151 m
- 48 m
- 0.19
- 331 m
- 0.023
- 10 s
- The person will move
- − 1.72 N
13.4 Friction on an Inclined Surface
- 0.54 m/s2
- 793 N
- 22.8°
Media Attributions
- “yellow and gray haul truck carrying sand and soil, Dumper, Coal Mining” from Wallpaper Flare is in the public domain.
- “Tribometre Vinci 1” by Léonard de Vinci is in the public domain.

