12 Power, Work & Energy

Resources

Equations Introduced and Used for this Topic:

  • [latex]a = \dfrac{\Delta v}{t}[/latex]
  • [latex]\Delta v = v_f - v_i[/latex]
  • [latex]v_f = v_i + a t[/latex]
  • [latex]d = v_i t + \frac{1}{2} a t^2[/latex]
  • [latex]F = m a[/latex]
  • Work [latex](W) = F \cdot d[/latex] or [latex]F d \cos ø[/latex]
  • [latex]E_p = m g h[/latex]
  • Power [latex](P) = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex]
  • [latex]P = \frac{1}{2}\varrho A v^3[/latex]
  • [latex]\vec{a} = \dfrac{\vec{\Delta v}}{t}[/latex]
  • [latex]v = \dfrac{(v_i + v_f)}{2}[/latex]
  • [latex]2 a d = v_f^2 - v_i^2[/latex]
  • [latex]d = \dfrac{(v+i v_f) t}{2}[/latex]
  • [latex]w = m g[/latex]
  • [latex]W = \Delta \text{ Energy}[/latex]
  • [latex]V[/latex] or [latex]V_g = g h[/latex]
  • [latex]E_k = \frac{1}{2} m v^2[/latex]
  • [latex]\text{Efficiency } = \text{ Output } \times 100%[/latex]
Equations a vt  vi d t
[latex]v_t = v_i + at[/latex] Not mentioned
[latex]2ad = v_{r}^{2} - v_{i}^{2}[/latex] Not mentioned
[latex]d = v_{i}t + \dfrac{1}{2} at^2[/latex] Not mentioned
[latex]d = \dfrac{(v_i + v_t)t}{2}[/latex] Not mentioned

Where…

  • [latex]P[/latex] is the power, measured in watts (W)
  • [latex]W[/latex] is work, measured in joules (J)
  • [latex]\varrho[/latex] is the density of the moving medium, measured in kilograms per metre cubed (kg/m3)
  • [latex]A[/latex] is the cross sectional area of the turbine, measured in metres squared (m2)
  • [latex]v[/latex] is the speed of the medium moving through the turbine, measured in metres per second (m/s)
  • [latex]v[/latex] is the speed of the object commonly measured in metres/second (m/s) or kilometres/hour (km/h)
  • [latex]\Delta \text{ Energy}[/latex] is the change in energy and can be any form of energy ([latex]E_p[/latex] or other forms), measured in joules (J)
  • [latex]E_p[/latex] is gravitational potential energy, measured in joules (J)
  • [latex]E_k[/latex] is kinetic energy, measured in joules (J)
  • [latex]V[/latex] or [latex]V_g[/latex] is the gravitational potential, measured in newtons per kilogram (N/kg)
  • [latex]\Delta h[/latex] is the change in vertical height, measured in metres (m)
  • [latex]F[/latex] is force, measured in newtons (N)
  • [latex]m[/latex] is mass, commonly measured in kilograms (Kg), grams (g) or tonnes (t)
  • [latex]g[/latex] or [latex]a_g[/latex] is the acceleration due to gravity and varies from 9.78 m/s2 (equator) to 9.83 m/s2 (North or South poles)… The average value of gravity is taken to be either 9.80 m/s2  or 9.81 m/s2
  • [latex]\vec{v}[/latex] is velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
  • [latex]v_i[/latex] is initial speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
  • [latex]\vec{v_i}[/latex] is initial velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
  • [latex]v_f[/latex] is final speed, commonly measured in metres/second (m/s) or kilometres/hour (km/h)
  • [latex]\vec{v_f}[/latex] is final velocity, commonly measured in metres/second (m/s) or kilometres/hour (km/h) and includes a direction
  • [latex]\Delta d[/latex] is distance travelled, commonly measured in metres (m), kilometres (km)
  • [latex]\vec{\Delta d}[/latex] is change in displacement, commonly measured in metres (m), kilometres (km) and includes a direction
  • [latex]a[/latex] is acceleration (deceleration is negative), measured in metres per second squared (m/s2)
  • [latex]\vec{a}[/latex] is vector acceleration, measured in metres per second squared (m/s2) and includes a direction
  • [latex]t[/latex] is time, commonly measured in seconds (s) or hours (h)

12.1 Power

Extra Help: Power

Equations Introduced or Used for this Section:

  • Work [latex](W) = F \cdot d[/latex] or [latex]F d \cos ø[/latex]
  • P [latex](P) = \vec{F} \cdot \vec{v}[/latex]
  • [latex]W = \Delta \text{ Energy}[/latex]
  • Power [latex](P) = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex]

Power is the rate at which work is done on a system or the rate of energy transfer between systems.  Rate refers to the amount of change in some measure of time.

1 watt = 1 joule/second

The concept of power originated from the studies of James Watt (1736-1819) as a way to compare the work done between steam engines and horses.  This comparison was done in the absence of modern SI units and no energy concept (James Joule was 8 months old when Watt passed away).  Instead, Watt defined his measure of power as the product of Force and Velocity, as a way of relating his steam engines to horses.  As such, the first measure of power used units of the pound to measure force and of inches per second, feet per minute and miles per hour.

Power [latex](P) = \text{ Force } \times \text{ Velocity}[/latex]

Watt’s work, therefore, was in defining power in terms of horsepower equivalents, specifically:

one horsepower (hp) equaled the power to raise 33000 pounds (lbs) 1 foot (ft) per minute (550 pounds 1 foot per second).

Legend has it that one of Watt’s first customers to whom he was trying to sell his significantly improved steam engine[1] asked Watt to compare it to a horse, which happened to be his strongest and most powerful horse.  Not only was Watt’s steam engine more powerful than this horse, the units of horsepower were then defined in terms of the power of this horse.

Since Watt’s original definition of the value of horsepower, two measures are commonly used:

Mechanical Horsepower  = 745.69987158227022 W (≈ 746 W)

and

Metric Horsepower = 735.49875 W (≈ 735 W)

In this textbook, mechanical horsepower will be used, since it is the most common in public usage. Electrical horsepower[2] is defined as 746 W.  Questions concerning power will use the following two equations:

  • Mechanical Power (Conservative Forces): [latex]P = \dfrac{\vec{F} \cdot \vec{d}}{t}[/latex]
  • Average Power: [latex]P = \dfrac{W}{t}[/latex]

Example 12.1.1

A 300 hp engine (horsepower) is equivalent to how many watts?

Solution

  • [latex]300 \text{ hp } = 300 \text{ hp } \times 746 \text{ W/hp}[/latex]
  • [latex]300 \text{ hp } = 224\;000 \text{ W}[/latex]

Example 12.1.2

If 3.0 MJ of work is done in 2 min what is the power involved?

Solution

Data:

  • [latex]P = \text{ Find}[/latex]
  • [latex]W = 3.0 \times 10^6 \text{ J}[/latex]
  • [latex]t = 2 \text{ min or } 120 \text{ s}[/latex]

Solution:

  • [latex]P = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex]
  • [latex]P = \dfrac{3.0 \times 10^6 \text{ J}}{120 \text{ s}}[/latex]
  • [latex]P = 25\;000 \text{ W or } 25 \text{ kW}[/latex]

Example 12.1.3

How much work can a 746 W motor do in 8.0 h?

Solution

Data:

  • [latex]P = \text{ Find}[/latex]
  • [latex]W = 3.0 \times 10^6 \text{ J}[/latex]
  • [latex]t = 2 \text{ min or } 120 \text{ s}[/latex]

Solution:

  • [latex]746 \text{ W } = \dfrac{W}{(8.0)(3600 \text{ s})}[/latex]
  • [latex]W = (746 \text{W})(8.0)(3600 \text{ s})[/latex]
  • [latex]W = 2.148 \times 10^7 \text{ J } (\approx 2.1 \times 10^7 \text{ J})[/latex]

Example 12.1.4

What minimum amount of time would it take a 200 W electric motor to do 12000 J of work?

Solution

Data:

  • [latex]P = 200 \text{ W}[/latex]
  • [latex]W = 12\;000 \text{ J}[/latex]
  • [latex]t = \text{ Find}[/latex]

Solution:

  • [latex]P = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex]
  • [latex]200 \text{ W } = \dfrac{12\;00 \text{ J}}{t}[/latex]
  • [latex]t = 12\;000 \text{ J } \div 200 \text{ W}[/latex]
  • [latex]t = 60 \text{ s}[/latex]

Example 12.1.5

 If only 84% of the force produced by a 1200 W electric motor is conservative, how much time is required to do 50000 J of work?

Solution

Data:

  • [latex]P = 1200 \text{ W}[/latex]
  • [latex]W = 50\;000 \text{ J}[/latex]
  • [latex]t = \text{ Find}[/latex]
  • [latex]\text{Efficiency } = 84\% \text{ or } 0.84[/latex]

Solution:

  • [latex]P = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex]
  • [latex](0.84)(1200 \text{ W}) = \dfrac{(50\;000 \text{ J})}{t}[/latex]
  • [latex]t = 50\;000 \text{ J } \div 1008 \text{ W}[/latex]
  • [latex]t = 49.6 \text{ s } (\approx 50 \text{ s})[/latex]

Exercise 12.1

  1. If [latex]3 \times10^6[/latex] J of work is done in 5 min what is the power involved?
  2. How much work can a 25 W motor do in 60 h?
  3. What is the minimum amount of time that it would take a 500 W electric motor to do 15 kJ of work?
  4. 120 hp (horsepower) is equivalent to how many watts?

12.2 Power & Change in Energy

Equations Introduced or Used for this Section:

  • [latex]E_p = m g h[/latex]
  • [latex]V \text{ or } V_g = g h[/latex]
  • [latex]E_k = \frac{1}{2} m v^2[/latex]

When the force used in power settings is conservative, then the work done by this power results in a change of mechanical energy and as a result changes either the kinetic, potential or both types of mechanical energies in a system.

Example 12.2.1

A conveyor belt carries a flat of 500 kg of asphalt shingles at a constant speed from the ground to the roof of a building 8.0 m above its initial position in 12.0 s.  Find the work done on the object and the power required to accomplish it. (Assume the initial and final speeds of these shingles are zero.)

Solution

First, find the Work:

  • [latex]W = \Delta \text{ Energy } = \Delta E_p \text{ or } m g \Delta h[/latex]
  • [latex]W = (500 \text{ kg})(9.8 \text{ m/s}^2)(8.0 \text{ m})[/latex]
  • [latex]W = 39\;200 \text{ J}[/latex]

Next, find the Power:

  • [latex]\text{Power } (P) = \dfrac{W}{t}[/latex]
  • [latex]P = \dfrac{39\;200 \text{ J}}{12.0 \text{ s}}[/latex]
  • [latex]P = 3270 \text{ W } (\approx 3300 \text{ W})[/latex]

Example 12.2.2

What is the power of an air cannon that can fire a seed pellet (mass 45.0 g) from rest to a speed of 140 km/h in 0.125 s?

Solution

  • [latex]\text{Power } (P) = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex] where [latex]\Delta \text{ Energy } = E_{kf} - E_{ki}[/latex] where [latex]E_{ki} = 0\text{ J}[/latex]
  • [latex]P = \dfrac{\frac{1}{2} m v_f^2}{t}[/latex]
  • [latex]P = \dfrac{\frac{1}{2} (0.045 \text{ kg})(38.9 \text{ m/s}^2)}{0.125 \text{ s}}[/latex]
  • [latex]P = 272 \text{ W}[/latex]

Example 12.2.3

What is the expected power output that can be achieved from an 85.0 m high hydroelectric dam[3] where the rate of water moving through the generators is 900 cubic metres per minute?  If the efficiency of electric power production is 32% efficient, what is the power produced?

Solution

  • [latex]\text{Power } (P) = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex] where [latex]\Delta \text{ Energy } = \Delta E_p[/latex] or [latex]m g \Delta h[/latex]
  • [latex]P = \dfrac{m g \Delta h}{t}[/latex]
  • [latex]P = \dfrac{(900 \text{ m}^3)(1000 \text{ kg/m}^3)(9.8 \text{ m/s}^2)(85 \text{ m})}{60 \text{ s}}[/latex]
  • [latex]P = 1.25 \times 10^7 \text{ W}[/latex] or [latex]12.5 \text{ MW}[/latex]

At 32% efficiency the power generated is:

  • [latex]P = (0.32)(12.5 \text{ MW})[/latex] or [latex]4.0 \text{ MW}[/latex]

Not covered in this textbook is the mechanical advantage of pulleys. Using pulleys one can increase the load being raised by using the same power source … In this case, you can see the amount of rope (displacement) that is being used by smaller forces to do the same amount of work.  This means that less powerful engines can be used to do the same amount of work, albeit at a slower rate.  In the example shown below, each pulley adds to the displacement that the force acts through.  In this case one only needs to consider the amount of energy lost to friction and such.

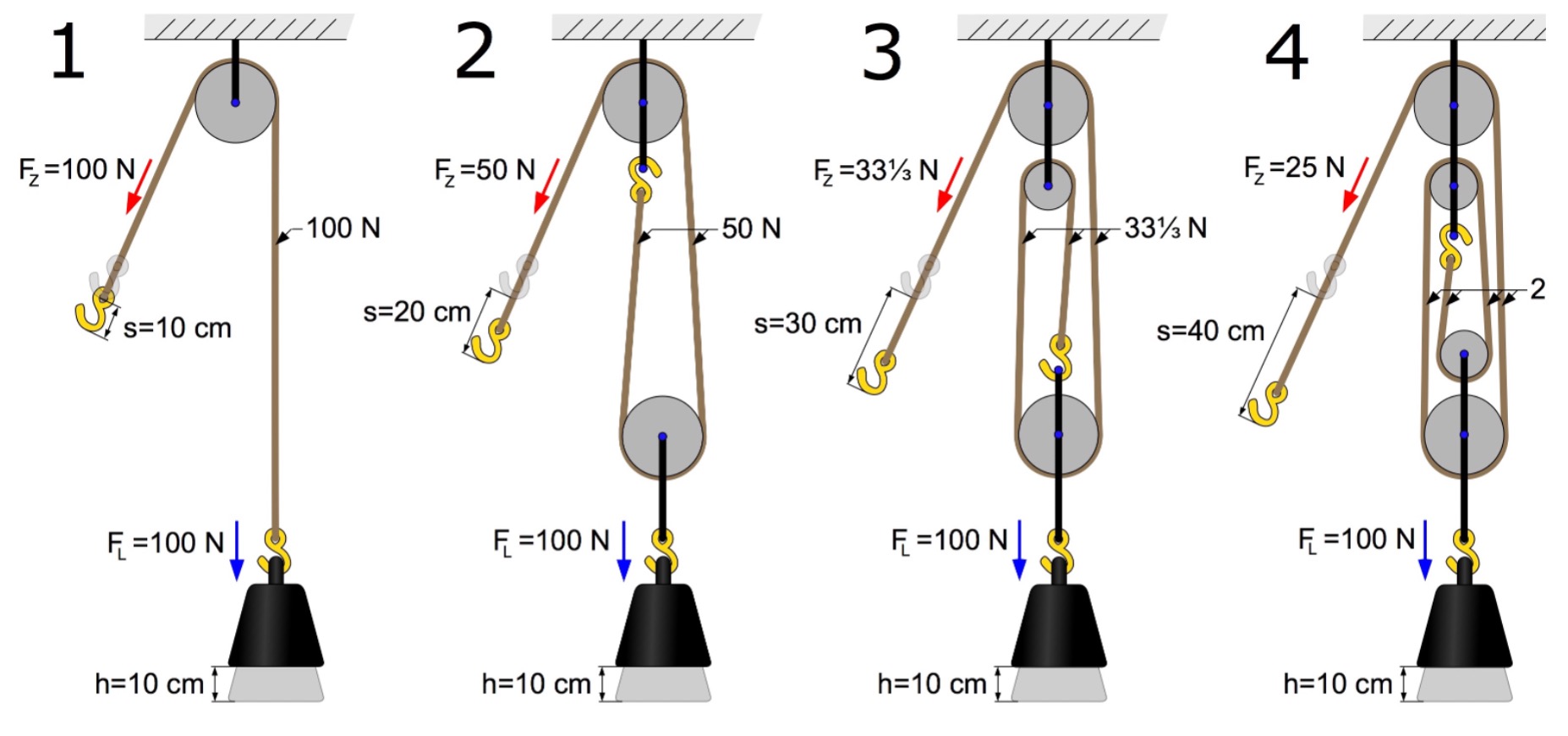
Exercise 12.2

  1. A world-class weight lifter can raise a 200 kg dumbbell from the floor to a height of 2.0 m in about 3.0 s.  What is this average power output during the lift?
  2. What power is required to raise a mass of 47 kg a final height of 12 m in 15 s? (The mass comes to a complete stop when the final height is reached.)
  3. A mass of 100 kg (at rest) is raised to a final resting position 8.0 m above its initial position in 7.0 s. Find the work done on the object and the power required to accomplish it.
  4. What is the power of an air cannon that can fire a seed pellet (mass 9.0 g) from rest to a speed of 185 m/s in 0.0065 s?
  5. What is the minimum power of an engine that can accelerate a 1600 kg pickup from 0 km/h to 110 km/h in 12 s?
  6. What is the power generated by 145 cubic metres of water falling through a potential difference of 392 m2/s2 each minute? (The mass of 1 cubic metre of water is 1 tonne.)
    1. What is the expected power output that can be achieved from a 120 m high hydroelectric dam, where the rate of water moving through the generators is 43 m3/s? (The mass of 1 cubic metre of water is 1000 kg or 1 tonne.)
    2. If the efficiency of this system is 45%, what is the power produced?

12.3 Power & Accelerated Motion

Equations Introduced or Used for this Section:

  • [latex]a = \dfrac{\Delta v}{t}[/latex]
  • [latex]\Delta v = v_f - v_i[/latex]
  • [latex]v_f = v_i + a t[/latex]
  • [latex]d = v_i t + \frac{1}{2} a t^2[/latex]
  • [latex]F = m a[/latex]
  • Work [latex](W) = F \cdot d[/latex] or [latex]F d \cos ø[/latex]
  • [latex]E_p = m g h[/latex]
  • Power [latex](P) = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex]
  • [latex]\vec{a} = \dfrac{\vec{\Delta v}}{t}[/latex]
  • [latex]v = \dfrac{(v_i + v_f)}{2}[/latex]
  • [latex]2 a d = v_f^2 - v_i^2[/latex]
  • [latex]d = \dfrac{(v+i v_f) t}{2}[/latex]
  • [latex]w = m g[/latex]
  • [latex]W = \Delta \text{ Energy}[/latex]
  • [latex]V[/latex] or [latex]V_g = g h[/latex]
  • [latex]E_k = \frac{1}{2} m v^2[/latex]

Power by definition when referring to the rate of work being done by a conservative force implies a change in mechanical energy, be it kinetic or potential (or both). When we restrict ourselves to only examining conservative forces, the system can be accelerating, changing vertical height at a constant velocity, or a more complicated combination of both kinetic and potential energies.

In the following examples and in using conservative forces, power is expanded to explore both accelerating and constant velocity situations.

Example 12.3.1

A motor is rated to deliver 8.4 kW.  What is the constant speed that this motor can raise a mass of 2100 kg?

Solution

  • [latex]\text{Power } (P) = \dfrac{W}{t} = \dfrac{\Delta \text{ Energy}}{t}[/latex] where [latex]\Delta \text{ Energy } = \Delta E_p[/latex] or [latex]m g \Delta h[/latex]
  • [latex]P = \dfrac{m g \Delta h}{t}[/latex] or [latex]P = m g v_{\text{up}}[/latex] or [latex]P = m g v_y[/latex]
  • [latex]8400 \text{ W } = (2100 \text{ kg})(9.8 \text{ m/s}^2)(v_y)[/latex]
  • [latex]v_y = 8400 \text{ W } \div [(2100 \text{ kg})(9.8 \text{ m/s}^2)][/latex]
  • [latex]v_y = 0.41 \text{ m/s}[/latex]

Example 12.3.2

A jet car used in drag racing was timed to have taken 3.4 seconds to travel 400.0 m from a stationary start.  If this car had a mass of 0.95 tonnes:

  1. Calculate the unbalanced force accelerating this car
  2. What power was developed?

Solution

Question (i): First we need to calculate the acceleration

  • First find the acceleration:
    • [latex]d = v_i t + \frac{1}{2} a t^2[/latex]
    • [latex]400 \text{ m } = (0 \text{ m/s})(3.4 \text{ s}) + \frac{1}{2} (a)(3.4 \text{ s})^2[/latex]
    • [latex]a = 69.2 \text{ m/s}^2[/latex]
  • Second find the force:
    • [latex]F = m a[/latex]
    • [latex]F = (950 \text{ kg})(69.2 \text{ m/s}^2)[/latex]
    • [latex]F = 65\;700 \text{ N } (\approx 66\;000 \text{ N})[/latex]

Question (ii):

  • [latex]\text{Power } (P) = \dfrac{W}{t} = \dfrac{\Delta F d \cos ø}{t}[/latex]
  • [latex]P = \dfrac{(65\;700 \text{ N})(400 \text{ m})\cos 0^{\circ}}{3.4 \text{ s}}[/latex]
  • [latex]P = 7.73 \times 10^6 \text{ W or } 7.73 \text{ MW } (\approx 7.7 \text{ MW})[/latex]

Example 12.3.3

A machine can produce 120 W of power.  If the machine is used for 12 s to raise a 50 kg mass straight upwards from a platform, where it is then released, at what speed would you expect this mass to impact the platform?

Solution

This problem is simpler than it looks. Since the work using conservative forces is a change in potential energy and in the second part where it is dropped, the potential energy changes to kinetic energy, then one can just use the work-energy theorem to solve this. There is no need to find out the change in potential energy, which we would then use to find the change in potential energy.

Therefore:

  • [latex]\text{Power } (P) = \dfrac{W}{t}[/latex] or [latex]W = P t[/latex]

Where:

  • [latex]W = \Delta E_k[/latex] or [latex]W = (E_{kr} - E_{ki})[/latex]

We are left with:

  • [latex]P t = \frac{1}{2} m v_f^2 - \frac{1}{2} m v_i^2[/latex]
  • [latex](120 \text{ W})(12 \text{ s}) = \frac{1}{2}(50 \text{ kg}) v_f^2 - \frac{1}{2}(50 \text{ kg})(0 \text{ m/s})^2[/latex]
  • [latex]v_f^2 = 1440 \text{ Ws } \div 25 \text{ kg}[/latex]
  • [latex]v_f= 7.6 \text{ m/s}[/latex]

Example 12.3.4

A 2.0 kW powered conveyer belt machine is angled at 28° above the horizontal.  At what constant speed can this belt be moving a 120 kg crate?

Solution

For this problem, we need to use the definition of  Power = Force × Velocity cos ø, where the angle ø in this problem is between the force and velocity, and is 90° – 28° or 62°.

Therefore:

  • [latex]\text{Power } (P) = F \cdot v \cos ø[/latex] where [latex]F = \text{ weight of } 120 \text{ kg}[/latex]
  • [latex]2000 \text{ W } = (120 \text{ kg})(9.8 \text{ m/s}^2)(v)\cos 62^{\circ}[/latex]
  • [latex]v = 2000 \text{ W } \div 522 \text{ J}[/latex]
  • [latex]v = 3.6 \text{ m/s}[/latex]

Exercise 12.3

  1. A motor is rated to deliver 10 kW.  What is the constant speed that this motor can raise a mass of [latex]2.75 \times 10^4[/latex] kg?
  2. What is the maximum possible constant speed that a 120 hp engine could lift a 4.00 ton (metric) mass straight up?
  3. What power is needed to run an elevator (maximum mass of 3500 kg, elevator and passengers) that rises at an average speed of 0.4 m/s?
  4. A cement pump can lift concrete at the rate of 3500 kg up 20 m every minute.
    1. What would be the minimum power of this pump?
    2. If this pump is 25% efficient, what minimum power must it be?
  5. A monster truck used in drag racing was timed to have taken 15.0 seconds to travel 400.0 m from a stationary start. If this truck had a mass of 2.40 tonnes:
    1. Calculate the unbalanced force accelerating this truck.
    2. What power was developed?
  6. An engine can produce 25000 W of power. If we assume that the conversion of engine power to mechanical energy of this 1000 kg car is 100% efficient, at what speed could this car be traveling after 15 s of full power, starting from rest?
  7. A machine can produce 40 W of power. If the machine is used for 15 s to raise a 20 kg mass straight upwards where it is released, at what speed would you expect this mass to impact its starting position?
  8. If a loaded semi (total mass = 20000 kg) is able to maintain a constant speed of 20 km/h up an 8° inclined road, what is the power output of the truck’s engine?
  9. What is the angle of a hill that a loaded pickup truck (m = 3600 kg) can climb at a constant speed of 45 km/h, if the 300 hp engine is 32% efficient?

Exercise 12.4

  1. It is claimed that large trees can evaporate as much as 1000 kg of water per day.  Assuming the average rise of water to be 10 m from the ground, what amount of energy must be supplied for this?  If we assume the source of this energy is from the Sun, what average amount of power must the tree receive over 12 hours of sunlight?
  2. An average human at rest radiates 75 W of power.  What amount of energy is radiated in eight hours?
  3. Power Output of the Sun…  The amount of solar energy striking the Earth is around 1350 watts per metre2.  Find the power output of our Sun. Under Business as Usual projections for global energy consumption, Energy usage is expected to rise from 589 EJ in 2016 to 1070 EJ in 2100 (E stands for [latex]exo \times 10^21[/latex])
Video to Watch: NASA – SDO Year 5

12.4 The Wind Resource

Several factors can affect wind speed and the ability of a turbine to generate more power.  For example, wind speed increases as the height from the ground increases.  If wind speed at 10 meters off the ground is 6 m/s it will be about 7.5 m/s at a height of 50 meters.  A 2003 Stanford University study examined wind speeds at higher elevations and found that as much as one quarter of the United States, including areas historically thought to have poor wind potential, is potentially suitable for providing affordable electric power from wind.  The rotors of the newest wind turbines can now reach heights up to 70 meters.  In addition to height, the power in the wind varies with temperature and altitude, both of which affect the air density.  Winter winds in Minnesota State will carry more power than summer winds of the same speed high in the passes of Southern States.

The more the wind blows, the more power will be produced, with the main drawback being inconsistent wind.  The term used to describe this is “capacity factor”, which is simply the amount of power a turbine actually produces over a period of time divided by the amount of power it could have produced if it had run at its full-rated capacity over that time period.

A more precise measurement of output is the “specific yield”. This measures the annual energy output per square meter of area swept by the turbine blades as they rotate.  Overall, wind turbines capture between 20 and 40 percent of the energy in the wind.  So, at a site with average wind speeds of 7 m/s, a typical turbine will produce about 1100 kilowatt-hours (kWh) per square meter of area per year.  If the turbine has blades that are 40 meters long, for a total swept area of 5029 square meters, the power output will be about 5.5 million kWh for the year.  An increase in blade length, which in turn increases the swept area, can have a significant effect on the amount of power output from a wind turbine.

Another factor in the cost of wind power is the distance of the turbines from transmission lines.  Although some large windy areas, particularly in rural parts of the High Plains and Rocky Mountains, are too far from power lines to be cost-effective today, the potential for these regions is still enormous.

A final consideration for a wind resource is the seasonal and daily variation in wind speed.  If the wind blows during periods of peak power demand, power from a wind farm will be valued more highly than if it blows in off-peak periods.  In California, for example, high temperatures in the central valley and low coastal temperatures near San Francisco cause powerful winds to blow across the Altamont in the summer, a period of high power demand.

Example 12.4.1

What is the kinetic energy or the air mass that passes through an offshore windmill at the Thorntonbank Wind Farm[4], having a rotor diameter of 126 m, if the wind speed averages 30 km/hr?  If we assume that current technology yields 45% power generation from this moving air mass, what power is produced per turbine?

Solution

Kinetic Energy:

  • [latex]E_k = \frac{1}{2} m v^2[/latex]
  • [latex]E_k = \frac{1}{2}(1.225 \text{ kg/m}^3)(8.33 \text{ m/s})^2[/latex]
  • [latex]E_k = 42.5 \text{ J/m}^3[/latex]

Power Produced (100% Efficient):

  • [latex]P = \frac{1}{2} \varrho A v^3[/latex]
  • [latex]P = \frac{1}{2} (1.225 \text{ kg/m}^3)(\pi)(126 \text{ m})^2(8.33 \text{ m/s})^3[/latex]
  • [latex]P = 1.7 \times 10^7 \text{ W or } 17.7 \text{ MW } (\approx 18 \text{ MW})[/latex]

Now, for 45% efficiency:

  • [latex]P = (0.45) 1.77 \times 10^7 \text{W}[/latex]
  • [latex]P = 7.95 \times 10^6[/latex] or [latex]7.95 \text{ MW } (\approx 8.0 \text{ MW})[/latex]

Wind Turbine Power:

Equations Introduced or Used for this Section:

[latex]P = \frac{1}{2} \varrho A C_P v^2 N_g N_b[/latex]

Where…

  • [latex]P[/latex] = power in watts
  • [latex]\varrho[/latex] = air density (about 1.225 kg/m3 at sea level at15°C)
  • [latex]A[/latex] = rotor swept area exposed to the wind (m2)
  • [latex]C_p[/latex] = coefficient of performance (0.59 {Betz limit} is the maximum theoretically possible 0.35 for a good design)
  • [latex]v[/latex] = wind speed in m/s
  • [latex]N_g[/latex] = generator efficiency (50% for car alternator, 80% or possibly more for a permanent magnet generator or grid-connected induction generator)
  • [latex]N_b[/latex] = gearbox/bearings efficiency (could be as high as 95% if good)
Temperature (°C) Density of Air (kg/m3)
−25 1.423
−20 1.395
−15 1.368
−10 1.342
−5 1.317
0 1.292
5 1.269
10 1.247
15 1.225
20 1.204
25 1.184
30 1.164
35 1.146

Exercise 12.4.1

  1. Using the graph and the chart on the previous page and assuming 100% efficiency
    1. What is the area of a 1.0 m circle?
    2. If the density of air at 20° C is 1.204 kg/m3 at sea level, what must be the minimum speed of the air for the 1.0 m diameter rotors to extract 0.4 kW?
    3. Using an air temperature of 20°C, calculate the minimum number of 11 m diameter rotors needed to generate 20 MW?
    4. What must be the speed of the air at −15°C to create 0.40 kW?
    5. Assuming the 10 m rotor produces 39.3 kW at an air temperature of 20°C.  What is the percent increase in power output if the temperature drops to -20°C?
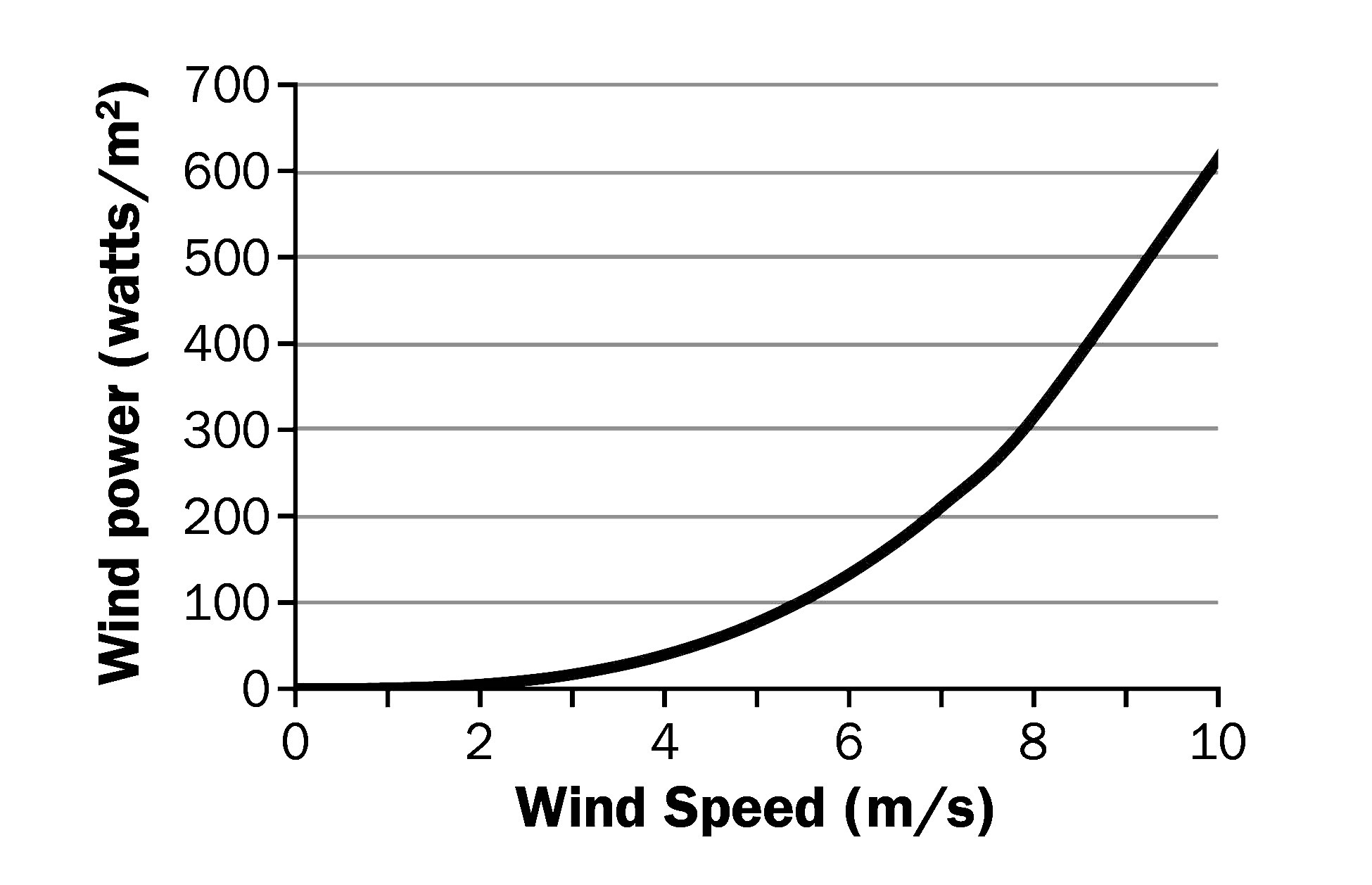
  2. The above graph shows the potential amount of energy from wind at 20° C.
    1. What would this curve look like if the air is hotter?
    2.  What would this curve look like if the air is colder?
    3. Notice the power at 8.0 m/s is around 300 W and at 10 m/s around 600 W.  Show how these numbers fit the equation [latex]P = \frac{1}{2} \varrho A v^3[/latex]
    4. How big would the rotor area of the windmill graphed above be if we assume it is 100% efficient?

(Realistically, [latex]C_p N_g N_b[/latex] = 0.27 or is around 27%)

12.5 Power from Ocean and River Currents

Research News: Hunt, J. D., et al. (2019) Using the jet stream for sustainable airship and balloon transportation of cargo and hydrogen

Ocean current speeds are generally lower than wind speeds.  This is important because the kinetic energy contained in flowing bodies is proportional to the cube of their velocity.  However another more important factor in the power available for extraction from a flowing body is the density of the material.  Water is about 835 times denser than wind, so for the same area of flow being intercepted the energy contained in a 19 km/h water flow is equivalent to that contained in an air mass moving at about 180 km/h.  Thus, ocean currents represent a potentially significant currently untapped reservoir of energy.

The total worldwide power in ocean currents has been estimated to be about 5000 GW with power densities of up to 15 kW/m2.  The relatively constant extractable energy density near the surface of the Florida Straits Current is about 1 kW/m2 of flow area.  It has been estimated that capturing just 1/1000th of the available energy from the Gulf Stream, which has 21 000 times more energy than Niagara Falls in a flow of water that is 50 times the total flow of all the world’s freshwater river, would supply Florida with 35% of its electrical needs.

Countries that are interested in and pursuing the application of ocean current energy technologies include the European Union, Japan and China.

Equations Introduced or Used for this Section:

[latex]P = \frac{1}{2} \varrho A v^3[/latex]

Where…

  • [latex]P[/latex] is power in watts
  • [latex]\varrho[/latex] is density of water (fresh water is roughly 1000 kg/m3).
  • [latex]A[/latex] is rotor swept area exposed to the water (m2)
  • [latex]v[/latex] is water speed (m/s)

Example 12.5.1

The Amazon River can reach an average current speed of 7 km/h at the height of the wet season.  What is the expected power that can be produced by an underwater turbine of diameter 2.0 m, assuming an efficiency of 42% for the power generating turbine? (Density of fresh water is around 1000 kg/m3)

Solution

  • [latex]P = \frac{1}{2} \varrho A v^3[/latex]
  • [latex]P = \frac{1}{2}(1000 \text{kg/m}^3) \pi (2.0 \text{ m})^2 (1.94 \text{ m/s})^3[/latex]
  • [latex]P = 12\;200 \text{ W or } 12.2 \text{ KW } (\approx 12 \text{ KW})[/latex]

Exercise 12.5

  1. The Fraser River has an average current speed ranging from 0.25 m/s to 1.25 m/s. What is the expected range of power that can be produced by an underwater turbine of diameter 1.5 m?  (Density of fresh water is around 1000 kg/m3)
  2. One of the strongest ocean currents is the Gulf Stream, which moves at speeds greater than 1.5 m/s. What is the maximum power that can be extracted by a 3.0 m diameter underwater turbine in this current?  How many of these turbines would be needed to replace a 50 MW coal-powered electric generator? (Density of ocean water is around 1003 kg/m3)
  3. What maximum power could be extracted from a 1.0 m diameter turbine in water moving at 20 km/h? (This is the speed of water falling 1.57 m.) How does this compare to what a similar sized turbine could extract from a Category 2 Hurricane where the wind (20° C) is moving at 160 km/h?
Article to Read: Scientists Develop Wave Energy Device That Generates Low-Cost Electricity

Exercise Answers

12.1 Power

  1. 10000 W
  2. 5.4 MJ
  3. 30 s
  4. 89500 W or 89.5 kW

12.2 Power & Change in Energy

  1. 1300 W
  2. 368 W
  3. 7840 J, 1120 W
  4. 23700 W
  5. 62000 W
  6. 0.947 MW
    1. 50.5 MW
    2. 22.8 MW

12.3 Power & Accelerated Motion

  1. 0.0371 m/s
  2. 2.28 m/s
  3. 13700 W or 13.7 kW
    1. 11400 W
    2. 45700 W
    1. 8500 N
    2. [latex]2.28 \times 10^5[/latex] W = 228 kW
  4. 27.4 m/s
  5. 7.7 m/s
  6. 152000 W = 152 kW
  7. 9.3°

12.4 Large Tree Evaporation, Human’s Radiated Heat, Power Output of the Sun

    1. 98000 J
    2. 2.27 W
  2. [latex]2.2 \times 10^6[/latex] J
  3. [latex]3.8 \times 10^{26}[/latex] W

12.4.1 The Wind Resource

    1. 0.785 m2
    2. 9.46 m/s
    3. 421 Rotors
    4. 9.18 m/s
    5. 45.4 kW
    1. The curve should flatten out due to decreased air density
    2. The curve should become steeper climb due to increased air density
    3. The ratio of 600 to 300 watts is roughly the same as the ratio of (10 m/s)3 to (8 m/s)3. Alternatively, on can look at the ratio of [latex]\dfrac{P}{v^3}[/latex] which equals 0.6 for both speeds.
    4. 0.997 m2 or 1 m2

12.5 Power from Ocean and River Currents

  1. 13.8 W at 0.25 m/s to 1.73 kW at 1.25 m/s
  2. 120 kW maximum power, approximately 4200 turbines to replace 50 MW
  3. 67 kW for water compared to 41 kW from a hurricane

Media Attributions

  1. Watt’s improvements on the steam engine efficiency are credited as the start of the expansion of the industrial revolution. The unit of watts to measure power was named in honor of James Watt for his steam engine improvements in 1889. ↵
  2. Wikipedia has an extensive list of the various form and measures of horsepower: https://en.wikipedia.org/wiki/Horsepower ↵
  3. Niagara Falls FAQ ↵
  4. Thorntonbank Wind Farm ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Foundations of Physics Copyright © by Terrance Berg is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book