Equations Introduced or Used in this Topic:

• [latex]F_c=\dfrac{mv^2}{r}[/latex]
• [latex]a_c=\dfrac{{v_c}^2}{r}[/latex]
• [latex]v_c=\dfrac{d}{t}=\dfrac{2\pi r}{T}[/latex]

• [latex]F_g=\dfrac{Gm_1{m}_2}{d^2}[/latex]
• [latex]F_f=\mu N\text{ or “}\mu mg\text{” (simplest case)}[/latex]
• [latex]F_f= \mu N\text{ where }N=mg\text{ cos ø}[/latex]
• [latex]w = mg[/latex]

• [latex]F_{fs} =\mu_sN[/latex]
• [latex]F_{fk}=\mu_kN[/latex]
• [latex]F_{fr} =\mu_rN[/latex]

Where…

• [latex]F_c[/latex] is the Centripetal Force (Centre Directed Force), measured in newtons (N)
• [latex]F_f[/latex] is the Force of Friction measured in newtons (N)
• [latex]F_{fs}[/latex] is the Force of Static Friction measured in newtons (N)
• [latex]F_{fk}[/latex] is the Force of Kinetic Friction measured in newtons (N)
• [latex]F_{fR}[/latex] is the Force of Rolling Friction measured in newtons (N)
• [latex]F_g[/latex] is the Gravitational Force of attraction measured in newtons (N)
• [latex]w[/latex] is Weight (it is a Force) measured in newtons (N)
• [latex]N[/latex] is the Normal Force measured in newtons (N)
• [latex]a_c[/latex] is the centre directed acceleration, measured in metres per second squared (m/s²)
• [latex]g[/latex] or [latex]a_g[/latex] is the Acceleration due to Gravity and varies from 9.78 m/s² (equator) to 9.83 m/s² (North or South poles)… The average value of gravity is taken to be either 9.80 m/s² or 9.81 m/s
• [latex]a_g[/latex] or [latex]g[/latex] is the Gravitational Field Strength of a body measured in metres/second squared (m/s²) or newtons per Kilogram (N/kg)
• [latex]v_c[/latex] is the Speed of the object moving in a circular path, measured in metres per second (m/s)
• [latex]m[/latex] is the Mass of the object moving in a circular path, measured in Kilograms (kg)
• [latex]m_1[/latex] & [latex]m_2[/latex] are the Masses of the two interacting bodies measured in Kilograms (kg)
• [latex]r[/latex] is the Radius of the circular path, measured in metres (m)
• [latex]d[/latex] is the Distance away from the Mass Centre of a Body (gravitational field) or the Distance between Mass Centres of Two Bodies (gravitational fields) measured in metres (m)
• [latex]µ_s, µ_k[/latex] & [latex]µ_r[/latex] are Coefficients of Friction and are magnitudes without units
• [latex]G[/latex] is Newton’s Gravitational Constant currently estimated to be 6.67408(31) × 10⁻¹¹ Nm²/kg²
• [latex]T[/latex] is the Period of the Simple Harmonic Oscillator, measuring the time it takes to make one complete motion measured in seconds (s)

18.1 Centripetal Force and Acceleration

Equations Introduced or Used for this Section:

• [latex]F_c=\dfrac{mv^2}{r}[/latex]
• [latex]{a}_{c}=\dfrac{{v_c}^2}{r}[/latex]
• [latex]v_c=\dfrac{2\pi r}{T}[/latex]

Centripetal Force is often confused with the term centrifugal force and it causes a number of problems for students learning the fundamental concepts of physics. To un-sort this confusion, one needs to explore circular motion while applying Newton’s Laws of Motion.

Newton’s first law states that every object will remain at rest or in uniform motion in a straight line unless compelled to change its state by the action of an external force.  This means that if an object is moving in a circular path, rather than in a straight line then there is some net force that is causing this to happen.  For a circular path, this force will always be directed to the centre of the circle.  This feature gives rise to the name of this force, specifically a Centre Directed Force or Centripetal Force ([latex]F_c[/latex]).

Newton’s second law, when applied to motion in a circle can be used to derive the centripetal force equation… [latex]F_{\text{net}} = ma[/latex].  This is simply done by replacing the linear acceleration with the value derived for centripetal acceleration…

[latex]a_c=\dfrac{{v_c}^2}{r}[/latex] combine to make [latex]F_c=\dfrac{mv^2}{r}[/latex]

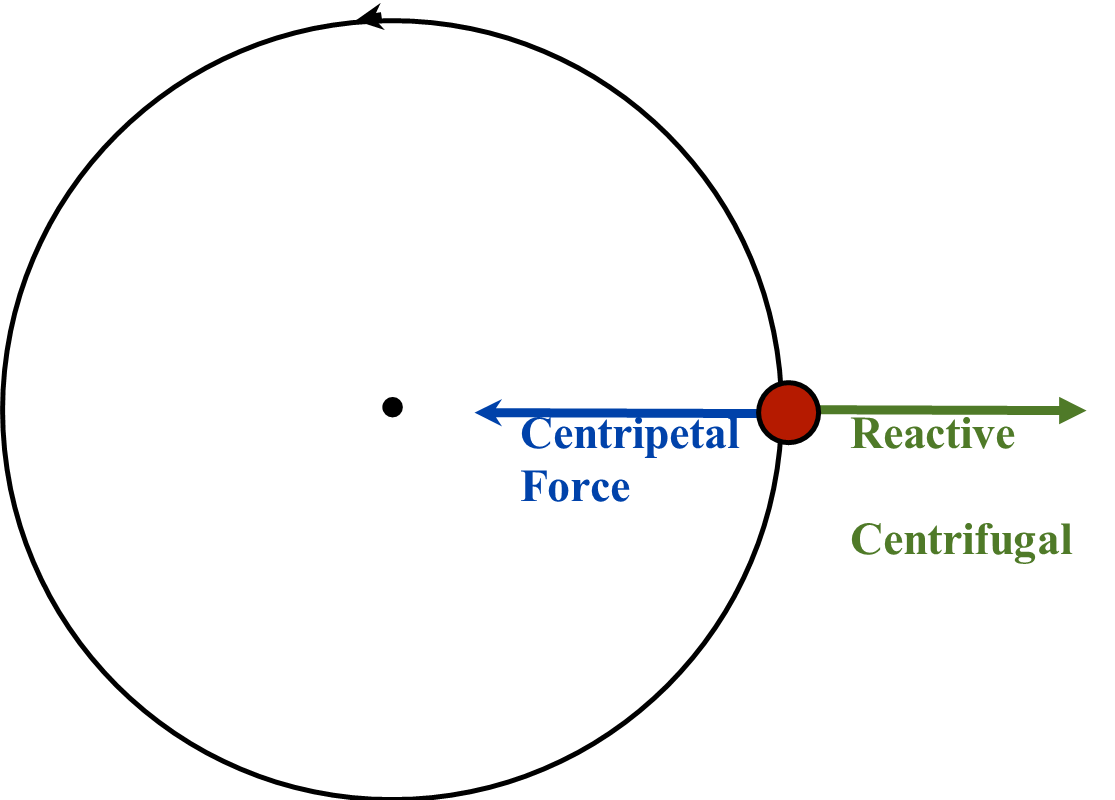
Newton’s third law states that for every action (force) in nature there is an equal and opposite reaction. This can help to understand where the idea of centrifugal force might be coming from. To move an object in a circular path a centre directed force is required. By Newton’s third law, there is a reactive force to the centripetal force which is called the reactive centrifugal force. One rarely sees reactive centrifugal force used in physics literature, however it is applied in some mechanical engineering settings where you have heard of it being used in laboratory devices such as the centrifuge.

Centripetal Acceleration is needed to move any object in a circular path. Similar to the unbalanced net force that is needed to cause an object to accelerate in a linear path, a centripetal net force will cause an object to accelerate to the centre of the curved path that it moves in. What is different from linear acceleration that results in the magnitude of a change in speed or velocity, centripetal acceleration can be as simple as the vector change in direction, such as occurring for the near circular orbit of Earth always changing in direction but maintaining a near constant speed as it orbits the Sun. Other objects such as comets having an elliptical orbit have a combination of both linear and centripetal acceleration and as such can be found to speed up and slow down, all the while they are changing the direction of their motion. The physics in this textbook will only consider centripetal and linear acceleration and not be analyzing combinations of the two.

As explained previously, centripetal acceleration can be found by replacing both linear acceleration and force in Newton’s Second Law with centripetal acceleration ([latex]a_c[/latex]) and centripetal force ([latex]F_c[/latex]). Doing this changes the equation of

[latex]F = m a[/latex] to [latex]F_c = m a_c[/latex]

Another variation of the equation for centripetal acceleration is one that comes from combining two centripetal force equations

[latex]F_c=\dfrac{mv^2}{r}[/latex] and [latex]F_c = ma_c[/latex]

The result of doing this yields a centripetal acceleration equation of the form

[latex]a_c=\dfrac{{v}^2}{r}[/latex]

18.2 Centripetal Force & Roller Coasters

Equations Introduced or Used for this Section:

• [latex]F_c=\dfrac{mv^2}{r}[/latex]
• [latex]w = mg[/latex]

The earliest looping roller coasters were given the name centrifugal railway, with the first of these built in 1843 in three cities in England. These rides were not actual roller coasters that we now think of, rather they were a simple race down a slope into a loop using centripetal force to hold both the car and the passenger in the car with the remaining kinetic energy being enough to get the car back up to the other side. These rides did not gain much popularity and were only used for a short period. A sketch of the Manchester centrifugal railway is shown below.

The first vertical loop roller coaster resurfaced a little over 50 years later in 1895 at Coney Island, NY and was given the name the “Flip Flap Railway”. This ride survived for less than 7 years before being shut down due to the extreme g-forces averaging 12 g’s on the riders. This caused riders significant discomfort and in a number of cases neck injuries from whiplash. The solution to salvaging this vertical loop ride was to design a tear drop shaped loop to reduce the g-forces in entering and leaving the loop.

The physics used to analyze these rides is to have the centripetal force remain greater than the force of gravity acting to pull the passengers and cars off the rails at the top of the loop.

18.3 Centripetal Force & Friction

Equations Introduced or Used for this Section:

• [latex]{F}_{c}=\dfrac{mv^2}{r}[/latex]
• [latex]F_f=\mu N\text{ or “}\mu mg\text{” (simplest case)}[/latex]

[latex]F_f= \mu N\text{ where }N=mg\text{ cos ø}[/latex]

• [latex]F_{fs} =\mu_sN[/latex]
• [latex]F_{fk}=\mu_kN[/latex]
• [latex]F_{fr} =\mu_rN[/latex]

When we consider vehicles, objects or persons moving in a circular path on a road or some surface, it is frictional forces that allow this curved motion to occur. In this section, only horizontal curves will be analyzed leaving banked curves to be covered in more advanced physics courses.

On horizontal surfaced curves the centripetal force allowing for curved motion to occur is friction. If we are looking at a vehicle such as a bus that needs to take a curve while driving along a road, the road conditions must be suitable that allow the friction between the tires and the road to be large enough to take this curve. The best friction for this is the static friction where the vehicle does not skid. The relationship for this looks like…

[latex]F_c= F_{fs}[/latex]

where the centripetal force allowing this bus to turn the corner is friction.

This equivalence equating the frictional force with the centripetal force works for all motion in a circular path where friction is the force that allows for these curved paths to be made.

The following examples all look at circular paths that are made using friction as the force to accomplish it.

18.4 Centripetal Force & Orbits

Equations Introduced or Used for this Section:

• [latex]{F}_{c}=\dfrac{mv^2}{r}[/latex]
• [latex]{F}_{g}=\dfrac{Gm_1{m}_2}{d^2}[/latex]

In 1609 and 1619 Johannes Kepler (1571-1630) building on the heliocentric concepts of Nicolas Copernicus (1473-1543) and the detailed telescopic data of Tycho Brahe (1546-1601) was able to arrive at three geometric equations that described the orbital motion of planets in a sun-centred solar system. His journey to arrive at these three laws is a complicated one that had him being expelled from one country due to his refusal to convert to Catholicism from his Calvinistic Christian upbringing, personal fights with Tycho Brahe in his desire to use Brahe’s data, all three children coming down with smallpox from his first wife (who died at an early age from Hungarian Spotted Fever), his first three children from his second marriage all dying in childhood and his mother being imprisoned for fourteen months as a suspected witch. Making sense of Kepler’s writings requires one to know, that in this time, there was no clear distinction between astronomy and astrology and that religion played a significant part in his writings.

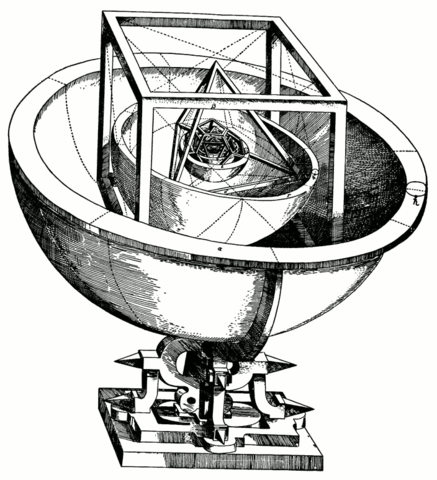
To Kepler himself, he believed that he had revealed God’s geometrical plan for the universe and were written in such a manner that they fit the earlier Greek conceptions of the five platonic solids that were thought to be the building blocks of the universe. Kepler revealed the sketch of his model in an earlier book, “Mysterium Cosmographicum” (The Cosmographic Mystery, 1597). It was this book where Kepler defended Tycho Brahe against the then claims of plagiarism, that Brahe allowed Kepler access to only his measurements of the planet Mars which was enough for Kepler to arrive at his three laws of planetary motion.

Kepler’s three laws of planetary motion can be stated as follows:

• All planetary orbits are elliptical in shape and have the Sun as one of the two foci. (For a circular orbit both foci are the same and at the centre of the circle). (The Law of Orbits)

• If one were to draw a line from the centre of the Sun to the centre of the orbiting planet, then the area swept out by the planet in orbit for any given amount of time, will equal the area swept out by the same planet in any given equal amount of time, no matter where the planet is in in that orbit. (The Law of Areas)

• If one were to take the squares of the period of motion of any planet and divide it by the cube of the average distance of the planet to the Sun, then one will arrive at the same constant of proportionality. (The Law of Periods)