17 Gravitational Forces and Fields
Resources
- Video to Watch: Mechanical Universe – Episode 8 – Apple and the Moon
- Extra Help: A-Level Physics Tutor
- Extra Help: Gravity is More Than a Name
- Article to Read: University of Otago (2018) Scientists invent easier, cheaper way to measure gravity
- Article to Read: Carnegie Institution for Science (2018) Outer solar system experts find ‘far out there’ dwarf planet
- Article to Read: NASA’s Goddard Space Flight Center (2018) NASA research reveals Saturn is losing its rings at ‘worst-case-scenario’ rate
Equations Introduced and Used in this Topic:
- [latex]F_g=\dfrac{Gm_1m_2}{d^2}[/latex]
- [latex]a_g \text{ or }g = \dfrac{Gm}{{d}^2}[/latex]
- [latex]\Delta V=-\dfrac{Gm}{d}[/latex]
G = 6.67408(31) × 10−11 Nm2/kg2 (round to needed accuracy)
Where…
- [latex]F_g[/latex] is the Gravitational Force of attraction, measured in newtons (N)
- [latex]G[/latex] is Newton’s Gravitational Constant, currently estimated to be 6.67408(31) × 10−11 Nm2/kg2
- [latex]m_1[/latex] & [latex]m_2[/latex] are the Masses of the two interacting bodies, measured in Kilograms (kg)
- [latex]a_g[/latex] or [latex]g[/latex] is the Gravitational Field Strength of a body, measured in metres/second squared (m/s2) or newtons per Kilogram (N/kg)
- [latex]d[/latex] is the Distance away from the Mass Centre of a Body (gravitational field) or the Distance between Mass Centres of Two Bodies (gravitational fields), measured in metres (m)
- [latex]∆V[/latex] is the potential difference measured in J/kg
| Body | Mass (kg) | Size (radius … m) | Orbit (radius … m)[1] |
|---|---|---|---|
| Sun | 1.9891 × 1030 | 6.980 × 108 | n/a |
| Mercury | 3.302 × 1023 | 2.439 × 106 | 5.791 × 1010 |
| Venus | 4.869 × 1024 | 6.052 × 106 | 1.082 × 1011 |
| Earth | 5.974 × 1024 | 6.371 × 106 | 1.496 × 1011 |
| Mars | 6.419 × 1023 | 3.390 × 106 | 2.279 × 1011 |
| Jupiter | 1.899 × 1027 | 6.991 × 107 | 7.783 × 1011 |
| Saturn | 5.685 × 1026 | 5.832 × 107 | 1.429 × 1012 |
| Uranus | 8.685 × 1025 | 2.536 × 107 | 2.871 × 1012 |
| Neptune | 1.028 × 1026 | 2.462 × 107 | 4.504 × 1012 |
| Moon | 7.349 × 1022 | 1.737 × 106 | 3.844 × 108 |
- Solar Mass (ms) is the mass of the Sun. 1 Solar mass = 1.98855 ± 0.00025 × 1030 kg
- Astronomical Unit (AU) is the distance from Earth to the Sun. 1 AU = 1.49597870700 × 1011 m
17.1 Gravitational Forces
- Article to Read: Physicists set limits on size of neutron stars
- Article to Read: Astronomers Detect Giant Rouge Planet Floating Near Our Solar System
- Article to Read: Boyle, R. (2018) These dusty young stars are changing the rules of planet-building
- Article to Read: The Guardian (2019) Nearby Galaxy set to collide with Milky Way, say scientists
- Article to Read: Where is the universe hiding its missing mass?
- Article to Read: GFZ GeoForschungsZentrum Potsdam (2019) What Earth’s gravity reveals about climate change
- Article to Read: Mass anomaly detected under the moon’s largest crater
Equations Introduced or Used for this Section:
[latex]F_{g}=\dfrac{Gm_1m_2}{{d}^2}[/latex]
| Body | Mass (kg) | Size (radius … m) | Orbit (radius … m) |
|---|---|---|---|
| Sun | 1.9891 × 1030 | 6.980 × 108 | n/a |
| Mercury | 3.302 × 1023 | 2.439 × 106 | 5.791 × 1010 |
| Venus | 4.869 × 1024 | 6.052 × 106 | 1.082 × 1011 |
| Earth | 5.974 × 1024 | 6.371 × 106 | 1.496 × 1011 |
| Mars | 6.419 × 1023 | 3.390 × 106 | 2.279 × 1011 |
| Jupiter | 1.899 × 1027 | 6.991 × 107 | 7.783 × 1011 |
| Saturn | 5.685 × 1026 | 5.832 × 107 | 1.429 × 1012 |
| Uranus | 8.685 × 1025 | 2.536 × 107 | 2.871 × 1012 |
| Neptune | 1.028 × 1026 | 2.462 × 107 | 4.504 × 1012 |
| Moon | 7.349 × 1022 | 1.737 × 106 | *3.844 × 108 |
Conceptions of Gravity and Astronomical Motion
Recorded concepts of gravity in Antiquity centre around the Greek philosopher Aristotle (384-322 BCE). Aristotle’s concept of gravity emerged from his understanding of natural motion in that all matter will rise or fall to its natural place in the universe. He contrasted this with forced or violent motion, where an object could be made to move until the agent causing it to move stopped. In Aristotle’s paradigm, gravity was a manifestation of objects moving to simply reach their natural place in the universe.
Aryabhata (476-550) held the view that the Earth rotates daily on its axis, but held onto the heliocentric model of the universe rotating around the Earth, as taught by the earlier pre-Ptolomaic Greek astronomers. While a great deal of Aryabhata’s work is lost, remnants indicate that he might have believed the planets move in elliptical orbits, a view that took nearly a thousand years to resurface in the works of Nicolaus Copernicus (1473-1543). There is also evidence that Aryabhata considered gravity to be an attractive force that allowed people to stand upright no matter where they were positioned on the Earth.
Galileo’s (1564-1642) was the first to record counter arguments to Aristotelian views on the movement of bodies to their natural place in the universe, through his experiments with the acceleration of falling bodies. Galileo’s concepts of acceleration were later confirmed by the works of Francisco Maria Grimaldi (1618-1663) and Giovanni Battista Riccioli (1589-1671). It was Riccioli who, through his analysis of free-fall motion in his attempts to find errors in Galileo’s theories, ended up finding the first measure of the acceleration of gravity. He estimated this to be 9.36 ± 0.22 m/s2, which is within a 5% error of today’s accepted value of 9.8 m/s2.
In working to quantify Robert Hooke’s (1635-1703) suggestion that gravitational force was an inverse square law relation , Isaac Newton (1643-1727) came up with the proportionality relation:
[latex]{F}_g∝ \dfrac{m_1{m}_2}{{d}^2}[/latex]
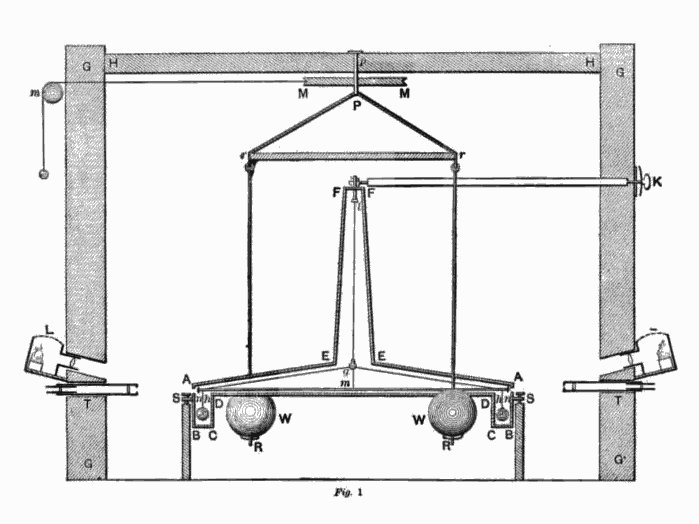
The first measured value of the constant G needed for Newton’s equation came from the 1797 experiments by Henry Cavendish (1731-1810) . This was accomplished by Cavendish’s measure of the density of the Earth, which he measured to be 5.48 times that of water. Cavendish’s work led other natural philosophers to estimate a value for G to be 6.754 × 10−11 N-m2/kg2 close to the current accepted value of 6.67428 × 10−11 N-m2/kg2. The Cavendish experiments are considered to be highlights of accuracy in laboratory science; his work is taught as representing a gold standard in experimental research.
Shown below is a sketch of the torsion apparatus that Cavendish used to measure the gravitational constant G.
- Article to Read: Anatomy of a fall: Giovanni Battista Riccioli and the story of g
- Hooke’s personality – Hooke is described as irascible, proud and prone to taking umbrage with intellectual competitors in his later years. Of note are his arguments with Isaac Newton on who should take credit over the discoveries in gravitation.
- Extra Help: The Apple, the Moon and the Inverse Square Law
- Extra Help: Cavendish and the Value of G
- Article to Read: Cavendish Experiment
- Article to Read: Is string theory still in the running for a theory of everything?
Example 17.1.1
What is the gravitational force of attraction between a 70 kg person resting on the Earth’s surface and the Earth?
Solution
Data:
- [latex]F_g[/latex] = Find
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m_1[/latex] = 5.974 × 1024 kg
- [latex]m_2[/latex] = 70 kg
- [latex]d[/latex] = 6.371 × 106 m
Solution:
- [latex]{F}_{g}=\dfrac{Gm_1{m}_2}{{d}^2}[/latex]
- [latex]{F}_{g}=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})(70\text{ kg})}{(6.371\times10^6\text{ m})^2}[/latex]
- [latex]F_g[/latex] = 690 N
Example 17.1.2
What is the gravitational force of attraction between the planet Mercury and the Sun?
Solution
Data:
- [latex]F_g[/latex] = Find
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m_1[/latex] = 1.981 × 1031 kg
- [latex]m_2[/latex] = 3.302 × 1023 kg
- [latex]d[/latex] = 5.791 × 1010 m
Solution:
- [latex]{F}_{g}=\dfrac{Gm_1{m}_2}{{d}^2}[/latex]
- [latex]{F}_{g}=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(1.981\times10^{31}\text{ kg})(3.302\times10^{23}\text{ kg})}{(5.791\times10^{10}\text{ m})^2}[/latex]
- [latex]F_g[/latex] = 1.31 × 1022 N
Example 17.1.3
What is the gravitational force of attraction between the electron and an alpha particle separated by 18 nm? (One nanometre (nm) = 1 × 10-9 m)
Solution
Data:
- [latex]F_g[/latex] = Find
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m_1[/latex] = 6.64 × 10−27 kg
- [latex]m_2[/latex] = 9.11 × 10−31 kg
- [latex]d[/latex] = 18 × 10−9 m
Solution:
- [latex]{F}_{g}=\dfrac{Gm_1{m}_2}{{d}^2}[/latex]
- [latex]{F}_\text{g}=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(6.64\times10^{-27}\text{ kg})(9.11\times10^{-31}\text{ kg})}{(18\times10^{-9}\text{ m})^2}[/latex]
- [latex]F_g[/latex] = 1.24 × 10−51 N
Exercise 17.1
- What is the gravitational force of attraction between a mass of 1.00 kg resting on the Earth’s surface and the Earth?
- What is the gravitational force of attraction between 2 apples that have a mass of 500 g and 400 g separated by 12 cm on a tree branch?
- Calculate the distance separating two ships that have a mass of 750 tonnes and 500 tonnes respectively, if the gravitational force of attraction between them is 10−6 newtons.
- What is the gravitational force of attraction between the electron and proton in a hydrogen atom? (The distance separating these two particles is called the Bohr radius.)
- What is the gravitational force of attraction between the planet Venus and the Sun?
- What is the maximum gravitational force of attraction between Jupiter and the Earth?
- One problem that plagues many entry level students is the comparison of the gravitational force of attraction that exists between the Earth and the Moon, and that between the Sun and the Moon. Find these two different forces of attraction and try to find an explanation why the Moon remains orbiting the Earth.
17.2 Gravitational Field Strength
Equations Introduced or Used for this Section:
[latex]a_g \text{ or }g=\dfrac{Gm}{d^2}[/latex]
In Newtonian mechanics or Classical Mechanics (non-relativistic) an equation quantifying gravitational strength of any body can be found by equating Newton’s Second Law and Newton’s Law of Gravitational Force. This can be shown as follows:
[latex]F_{\text{net}}= ma\text{ or }F_g = mg\text{ is equated to }F_{g}=\dfrac{Gm_1{m}_2}{{d}^2}[/latex]
This means that …
[latex]mg=\dfrac{Gm_1{m}_2}{{d}^2}[/latex]
cancelling out the common mass leaves us with …
[latex]g=\dfrac{Gm_1}{{d}^2}[/latex]
Applying the conventional negative direction to this derivation we are left with
[latex]g=-\dfrac{Gm_1}{{d}^2}[/latex]
In most classical mechanics questions this negative value is left out and the strength of gravity is just given as a scalar value.
The units of gravitational field strength can be either m/s2 or N/kg. This equation relates to the gravity at any distance away from a point mass and is an inverse square law relationship.
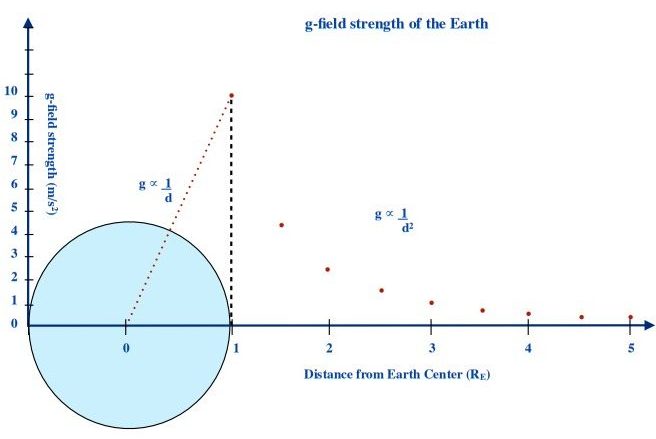
[latex]g ∝ \dfrac{1}{{d}^2}[/latex]
When we look at the gravitational field strength as we move towards the centre of the mass, the gravitational field strength drops inversely to zero. Beneath the planet’s surface gravity is an inverse linear relationship.
[latex]g ∝ \dfrac{1}{{d}}[/latex]
Example 17.2.1
What should be the surface gravity of the planet Venus?
Solution
Data:
- [latex]a_g[/latex] or [latex]g[/latex] = Find
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m[/latex] = 4.869 × 1024 kg
- [latex]d[/latex] = 6.052 × 106 m
Solution:
- [latex]a_g \text{ or }g = \dfrac{Gm}{{d}^2}[/latex]
- [latex]g=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(4.869\times10^{24}\text{ kg})}{(6.052\times10^6\text{ m})^2}[/latex]
- [latex]g[/latex] = 8.87 m/s2… (N/kg)
Example 17.2.2
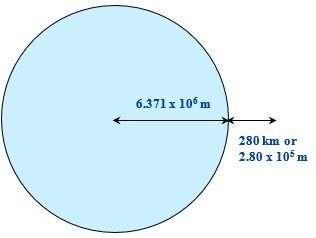
What is the acceleration due to gravity at an orbit of 280 km above the Earth’s surface[2]?
Now… [latex]d[/latex] = radius of the Earth + distance to orbit
- [latex]d[/latex] = 280 km + 6.371 × 106 m or 6.651 × 106 m
 Finally …
Finally …
- [latex]a_g[/latex] or [latex]g[/latex] = Find
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m[/latex] = 5.974 × 1024 kg
- [latex]d[/latex] = 6.651 × 106 m
Solution:
- [latex]a_g \text{ or }g = \dfrac{Gm}{{d}^2}[/latex]
- [latex]g=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})}{(6.651\times10^6\text{ m})^2}[/latex]
- [latex]g[/latex] = 9.01 m/s2 … (N/kg)
Example 17.2.3
If a rocket is orbiting at a distance from Earth where the gravity is 0.90 gs, how much further away must it move away from the Earth to experience a gravity of 0.42 gs?
Solution
First: d for 0.90 g’s
- [latex]a_g[/latex] or [latex]g[/latex] = 0.90 g’s
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m[/latex] = 5.974 × 1024 kg
- [latex]d[/latex] = Find
Solution:
- [latex]a_g \text{ or }g = \dfrac{Gm}{{d}^2}[/latex]
- [latex](0.90)(9.80\text{ m/s}^2)=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})}{d^2}[/latex]
- [latex]\text{d}^2=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})}{(0.90)(9.80\text{ m/s}^2)}[/latex]
- [latex]d^2[/latex] = 4.52 × 1013 m2
- [latex]d[/latex] = 6.72 × 106 m
Second: d for 0.42 g’s
- [latex]a_g[/latex] or [latex]g[/latex] = 0.42 g’s
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
- [latex]m[/latex] = 5.974 × 1024 kg
- [latex]d[/latex] = Find
Solution:
- [latex]a_g \text{ or }g = \dfrac{Gm}{{d}^2}[/latex]
- [latex](0.42)(9.80\text{ m/s}^2)=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})}{d^2}[/latex]
- [latex]{d}^2=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})}{(0.42)(9.80\text{ m/s}^2)}[/latex]
- [latex]d^2[/latex] = 9.69 × 1013 m2
- [latex]d[/latex] = 9.84 × 106 m
Finally…
- [latex]\Delta d[/latex] = d90 − d42
- [latex]\Delta d[/latex] = 9.84 × 106 m − 6.72 × 106 m
- [latex]\Delta d[/latex] = 3.12 × 106 m
Exercise 17.2
- What is the surface gravity of a 100 kg pumpkin of radius 0.75 m?
- What should be the surface gravity of the planet Uranus?
- What would be the surface gravity at the outer edge of the Sun?
- What is the acceleration due to gravity at an orbit of 300 km above the Earth’s surface? This distance is termed the Low Earth Orbital (LEO). Ships orbiting at this distance need to be boosted higher in orbit at regular intervals due to air resistance from the very weak atmosphere that exists at this distance. (Atmospheric pressure at this distance averages 10−8 Pa, compared to 1.013 × 105 Pa at the Earth’s surface.)
- What acceleration does the Moon experience due to the Earth’s gravity, in its orbit around the Earth? What acceleration does the Earth experience due to the Moon’s gravity?
- At what distance away from the Earth has the net acceleration due to gravity fallen to ½ g?
- What is the acceleration due to gravity experienced by an Earth orbiting satellite at a distance of 1 Earth radius above the surface?
- What distance above the Earth’s surface must one travel to experience a reduced Earth gravity of 0.7 g’s?
- If a shuttle is orbiting at a distance from Earth where the gravity is 0.8 gs, how much farther away must it move from the Earth to experience a gravity of 0.6 gs?
17.3 Gravitational Potential
Article to Read: Gravitational Waves Reveal the Hearts of Neutron Stars
Equations Introduced or Used for this Section:
[latex]ΔV =-\dfrac{Gm_1}{d}[/latex]
In classical mechanics, the gravitational potential at any location equals the work per unit of mass needed and moves the object from a fixed reference position to a final position within or outside a gravitational field. Typically, the gravitational potential refers to some final position infinitely far away from the gravitational source. As a result, at an infinite distance away the potential energy of any object in relation to its source position is zero. (Epf = 0). Also note that the movement that changes an object’s potential energy must be either toward or away from the gravitational source.
If we look at the work needed to move an object away from a gravitational source, we start by using the conservation of mechanical energy … Specifically:
[latex]W = ∆\text{Energy}[/latex]… Since the [latex]∆ E[/latex] is a change in potential energy… [latex]W = E_{pf} −E_{pi}[/latex]
This can be simplified for cases where the object is moved to an infinite distance away to
[latex]W = - E_{pi}\text{ since }E_{pf} = 0[/latex]

We can expand [latex]W = - E_{pi}[/latex] to [latex]W = - m g h_i[/latex] and replace gravity with [latex]g= - \dfrac{Gm_1}{d}[/latex]
This yields: [latex]W= - m\dfrac{Gm_1}{d}{h}_{i}[/latex]… And since hi and d2 are measuring the same distance, we can cancel common terms.
This leaves us with [latex]W=-\dfrac{Gm_1{m}_2}{d}[/latex]
The derivation of gravitational potential is almost complete. What remains is to isolate the second mass m2.
Isolating m2 from the main equation leaves us with: [latex]W=-\dfrac{Gm_1}{d}({m}_2)[/latex]
The symbol we will use for gravitational potential is the same as the one we use for electric potential. Gravitational potential (∆V) where [latex]\Delta V=-\dfrac{Gm_1}{d}[/latex]
In this case, the work done (joules) to move an object infinitely away from a measurable gravitational field is found by the equation:
[latex]W=-\dfrac{Gm_1}{d}({m}_2)[/latex] or [latex]V=−\Delta V (m_2)[/latex]
Likewise the gravitational potential energy of an object removed from the influence of a planetary or sun’s gravitational field is also found by:
[latex]\Delta E_p=-\dfrac{Gm_1}{d}({m}_2)[/latex] or [latex]\Delta E_p=-\Delta V (m_2)[/latex]
How do we understand the negative value that shows up in these equations?
- As you move away from a gravitational field, you will need energy to escape. You can consider this energy to be lost.
- As you move into a gravitational field, you will be gaining energy, which is added to your mass.
Equation Summary: To move any mass away from a gravitational source, use:
[latex]W=-\dfrac{Gm_1{m}_2}{d}[/latex] or [latex]\Delta E_p=-\dfrac{Gm_1{m}_2}{d}[/latex]
Using ∆V = [latex]-\dfrac{Gm_1}{d}[/latex] the above equations shorten to:
[latex]W=-\Delta Vm_2[/latex] or [latex]\Delta E_p=-\Delta Vm_2[/latex]
Example 17.3.1
What is the gravitational potential at an orbital distance of 280 km above the Earth’s surface?
Solution
Data:
- [latex]\Delta V[/latex] = Find
- [latex]d[/latex] = 280 km + 6.371 × 106 m or 6.651 × 106 m
- [latex]m[/latex] = 5.974 × 1024 kg
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
Solution:
- [latex]\Delta V=-\dfrac{Gm_1}{d}[/latex]
- [latex]\Delta V=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})}{6.651\times10^6\text{ m}}[/latex]
- [latex]\Delta V[/latex]= −5.99 × 107 J/kg
Example 17.3.2
How much work must be done for the space shuttle (mass = 2030 t) orbiting 280 km above the Earth’s surface to permanently escape the Earth?
Solution
Data:
- [latex]W[/latex] = Find
- [latex]d[/latex] = 280 km + 6.371 × 106 m or 6.651 × 106 m
- [latex]m_1[/latex] = 6.419 × 1023 kg
- [latex]m_2[/latex] = 2030 × 103 kg
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
Solution:
- [latex]W[/latex] = [latex]-\dfrac{Gm_1{m}_2}{d}[/latex]
- [latex]W[/latex] = [latex]-\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(5.974\times10^{24}\text{ kg})(2030\times10^3\text{ kg})}{6.651\times10^6\text{ m}}[/latex]
- [latex]W[/latex] = 1.22 × 1014 J
Example 17.3.3
What is the gravitational potential of a rocket ship sitting on the surface of the planet Mars?
Solution
Data:
- [latex]\Delta V[/latex] = Find
- [latex]m_1[/latex] = 6.419 × 1023 kg
- [latex]d[/latex] = 3.390 × 106 m
- [latex]G[/latex] = 6.67 × 10−11 Nm2/kg2
Solution:
- [latex]\Delta V=-\dfrac{Gm_1}{d}[/latex]
- [latex]\Delta V=\dfrac{(6.67\times10^{-11}\text{ Nm}^2\text{/kg}^2)(6.419\times10^{23}\text{ kg})}{3.390\times10^6\text{ m}}[/latex]
- [latex]\Delta V[/latex] = −1.26 × 107 J/kg
Exercise 17.3
- What is the gravitational potential at an orbital distance of 300 km above the Earth’s surface?
- How much work must be done for Elon Musk’s 2008 Tesla Roadster (mass = 1300 kg) at an orbital distance of 300 km above the Earth’s surface to permanently escape the Earth?
- What is the gravitational potential of a rocket ship sitting on the moon’s surface?
- What is the gravitational potential for a rocket launched from the Earth’s orbit around the Sun to escape the Sun’s gravitational field?
17.4.1 Earth-Moon Gravity Neutral Point
Between the Earth and the Moon, there exists a “fluctuating” position where the gravitational fields of the Earth and Moon balance each other out. This position is defined as the Earth-Moon Gravity Neutral Point. Described by an equation, this position can be found from
[latex]g_{\text{ Earth}}= g_{\text{ Moon}}[/latex]
where [latex]g=\dfrac{GM}{{d}^2}[/latex]
Technically, this position is where the gravitational fields from both the Moon and the Earth balance each other out, meaning that any object in this position having no velocity relative to the Earth and Moon should stay in that position without being pulled to the Earth or the Moon. Should any spaceship reach this position headed to Earth or the Moon, it would then be able to fall to either side of this position without using any more fuel for thrust. This can be looked at as a moving vehicle at the top of a hill … If the vehicle is moving in any direction down the hill when at the top, then the vehicle will be able to roll down hill without using any fuel. If the vehicle is stopped at the top of the hill, then it should be able to remain stationary unless some external unbalanced force acts upon it, which would then act to nudge the vehicle downhill in one of the two directions. This position is termed fluctuating because of a number of factors which are described by NASA’s David Ellis.
The gravity neutral position is visually shown by mapping the variable strength of the Earth’s gravitational field as one heads to the Moon, overlaid by the variable strength of the Moon’s gravitational field as one heads back to the Earth. The intersection of these two gravitational fields’ lines marks the approximate position. Due to fluctuations in the location of this position, any spaceship parked there would need corrections by booster rockets to remain in the region of neutral gravity.

Exercise 17.4
- Using your equations for the gravitational fields of the Earth and the Moon, calculate the distance from the Earth that this point exists.
Exercise Answers
17.1 Gravitational Force
- 9.82 N
- 9.3 × 10−10 N
- 5000 m or 5.00 km
- 3.63 × 10−47 N
- 5.52 × 1022 N
- 1.91 × 1018 N
- Earth-Moon: 2.02 × 1020 N,
Sun-Moon: 4.39 × 1020 N
17.2 Gravitational Field Strength
- 1.2 × 10−8 m/s2
- 9.01 m/s2
- 272 m/s2
- 8.96 m/s2
- Moon: 2.70 × 10−3 m/s2
Earth: 3.32 × 10−5 m/s2 - 9.01 × 106 m from the Earth’s centre or 2650 km above the surface
- 2.45 m/s2 or 1/4 g’s
- 1.25 × 106 m or 1250 km
- 3.49 × 105 m
17.3 Gravitational Potential
- [latex]\Delta V[/latex] = − 5.97 × 104 J/kg
- [latex]W[/latex] = − 7.77 × 1010 J
- [latex]\Delta V[/latex] = − 2.82 × 106 J/kg
- [latex]\Delta V[/latex] = − 8.87 × 108 J/kg
17.4.1 Earth-Moon Gravity Neutral Point
- Distance from the Earth = 3.46 × 108 m & Distance from the Moon = 3.84 × 107 m
Media Attributions
- “Cavendish Experiment” by Henry Cavendish is in the public domain.
- “Gravity Potential” by AllenMcC. is licensed under a CC BY-SA 3.0 licence.
-
“Earth moon gravitational potential” by MikeRun is licensed under a CC BY-SA 3.0 licence.
- The radius of orbits are given around the Sun, except the moon, which is given as its orbit around the Earth. ↵
- The Earth is losing 50,000 tonnes of mass every single year. Solution The Earth gains 40000 tonnes of space dust and asteroid. The Earth loses 16 tonnes due to the fission in the Earth’s core. The Earth loses 95000 tonnes of escaped hydrogen. The Earth loses 1600 tonnes of escaped helium. The net loss of Earth Mass is about 0.000000000000001% each year. Source - Earth loses 50,000 Tonnes of Mass Every Year ↵

