Equations Introduced and Used in this Topic:

• [latex]\vec{E}=\dfrac{V}{\vec{d}}[/latex]
• [latex]F_{el}=q\vec{E}[/latex]

[latex]W=\Delta E=qV\text{ or }q\vec{E}\vec{D}[/latex]

Where…

• [latex]F_{el}[/latex] is the Electric Force, measured in newtons (N)
• [latex]V[/latex] is the voltage, measured in volts (V)
• [latex]\vec{E}[/latex] is the Electric Field, measured in newtons per coulomb (N/C) or volts per metre (V/m)
• [latex]q[/latex] is the Charge, measured in coulombs (C)
• [latex]∆E[/latex] is the Energy, measured in joules (J)
• [latex]d[/latex] is the Parallel Plate Separation, measured in metres (m)
• [latex]W[/latex] is the Change in Energy of any particle moving up or down the field lines

21.1 Energy Change of Charge moving through a Uniform Electric Field

Equations Introduced:

[latex]ΔE = qV[/latex]

Energy Unit: One electron volt (eV) is the energy gained by one electron or proton that is accelerated through a potential difference of one volt.

[latex]1\text{ eV}= 1.602 \times 10^{−19}\text{ J}[/latex]

Historical Development

The electric field created between two parallel charged plates is different from the electric field of a charged object. A proper discussion of uniform electric fields should cover the historical discovery of the Leyden Jar , leading to the development of capacitors and, in later works, parallel charged plates, which have been central to many developments in physics.

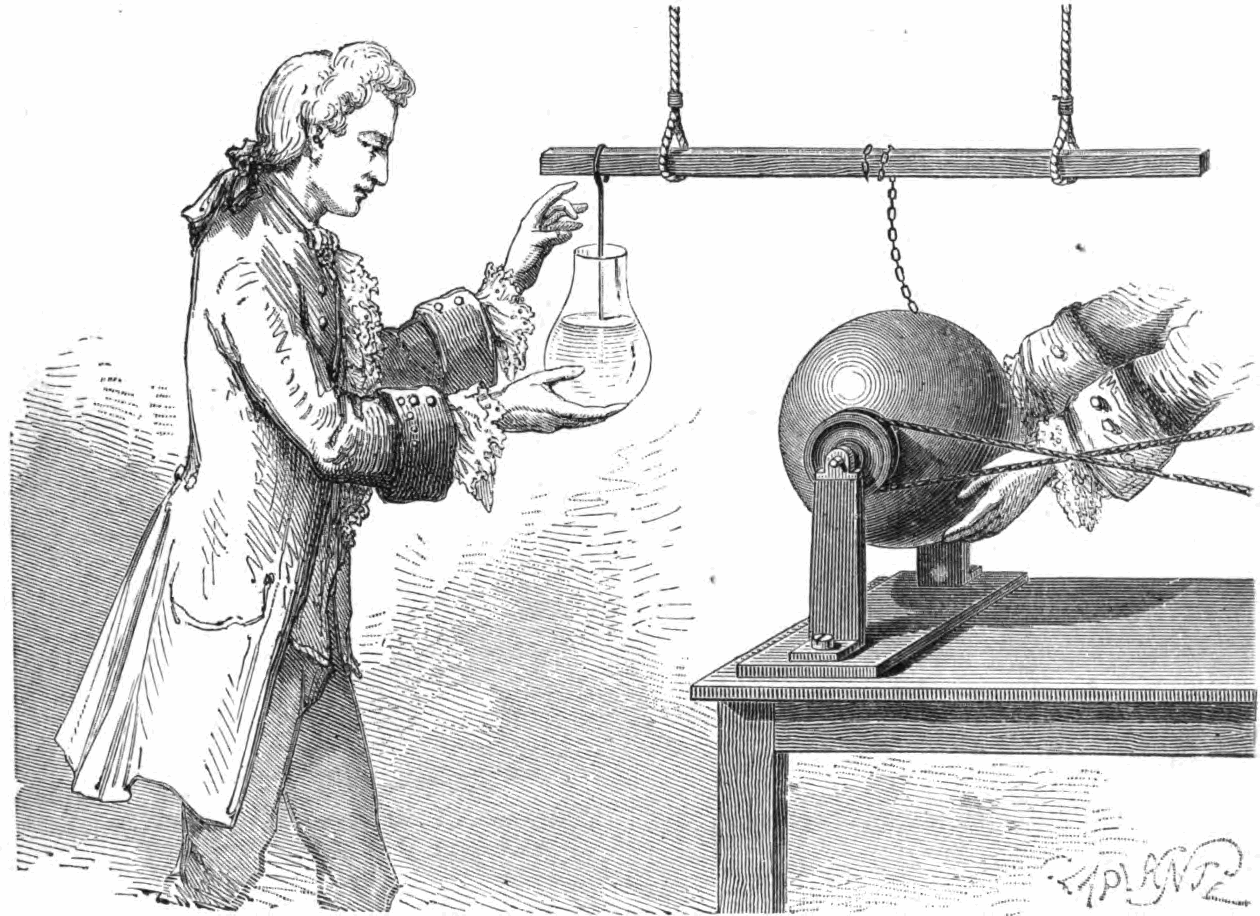
The ability to store electric charge was accidentally discovered in 1746, by Andreas Cunaeus, a lawyer visiting the laboratory of Pieter von Muschenbroek (1692-1761) in Leyden, Holland.  This discovery arose from Cunaeus’s attempts to “condense” electricity into a glass filled with beer and who had failed to properly place himself on an insulated stool. The charging device was a rotating glass sphere that generated a static charge by the hands rubbing it, which was then transferred through a chain to a suspended metal bar, and then into a hanging wire into the hand-held glass of beer. This arrangement allowed the glass to build up a large charge in the beer, with an equal and opposite charge built in Cunaeus’s hand holding the glass. When Cunaeus began to pull the wire out of the beer he received a severe shock, far worse than the electrostatic machine could give. It took Cunaeus two full days to recover from this accident.

Musschenbroek was so distressed by the severity of the shock he later received from the device that he wrote, warning of the dangers of this device, “I would not take a second shock for the crown of France”. Reports of the experiment became widely circulated, and scientists began to investigate the charge storage ability of these “Leyden Jars”. Eventually the water that filled the jar was replaced by foil coatings on both the inside and outside of the jar.

Electric charge storage devices are suspected to have been created far earlier than the Leyden Jar in 1746.  Nicholas Tesla speculated in a 1915 article that the Ark of the Covenant was in fact a capacitor, deadly to touch… “The records, though scanty, are of a nature to fill us with conviction that a few initiated, at least, had a deeper knowledge of amber phenomena. To mention one, Moses was undoubtedly a practical and skillful electrician far in advance of his time. The Bible describes precisely, and minutely, arrangements constituting a machine in which electricity was generated by friction of air against silk curtains, and stored in a box constructed like a condenser. It is very plausible to assume that the sons of Aaron were killed by a high-tension discharge, and that the vestal fires of the Romans were electrical.”

The Leyden Jar became one of great importance in the early development of the knowledge of static electricity since, before this, no device had been created that allowed for the storage of any significant amount of electricity.  These early devices allowed for the storage of between 20 000 and 60 000 volts, which had varying amounts of energy, all depending on the amount of the charge stored. It was such a device that Benjamin Franklin used with his “famous kite in a thunderstorm” that was used to store the electric charge of part of a lightning bolt.

By the 1850s, the Leyden Jar was in quite common by researchers who were aware of the significant risks involved.  Soon, the Leyden jar was used in spark-gap transmitters and electrotherapy, and was soon replaced by the more versatile capacitor.

The physics equation used for the simplest case of the constant electric field created in the storage of electric charge in a capacitor is as follows:

[latex]\vec{E}=\dfrac{V}{\vec{d}}[/latex]

This equation is valid for the central portion of very large parallel charged plates as the electric field is distorted near the ends or boundaries of the plates. As in electrostatic fields the electric field is measured in N/C, voltage (or Potential Difference between the parallel charged plates) is measured in volts and the distance separating the parallel charged plates is measure in metres. The negative sign in this equation is a relic of the definition of the movement of positive charge, since positive charges would be repelled by a positively charged plate. The following examples concern themselves with the energy contained in a constant electric field:

21.2 Uniform Electric Fields (Parallel Charged Plates)

Equations Introduced or Used for this Section:

• [latex]{F}_{el}=q\vec{E}[/latex]
• [latex]W=\Delta E=qV\text{ or }q\vec{E}\vec{D}[/latex]

One of the interesting outcomes arising from the discovery of the constant electric field between two charged plates is the motion of charged particles moving between them. For these parallel charged plates the electric field is quantified as:

[latex]\vec{E}=\dfrac{V}{\vec{d}}[/latex]

This electric field is roughly constant between the two plates, which when combined with electric force can be used to cover both linear and projectile motion, impulse, momentum, kinetic and potential energy. The equations used are nearly identical to those used in previous topics, but one must be mindful that these only work in non-relativistic settings where v < 0.1 c, which at this speed generally amounts to a 1% error. Consider a negative charged particle between the parallel charged plates shown below:

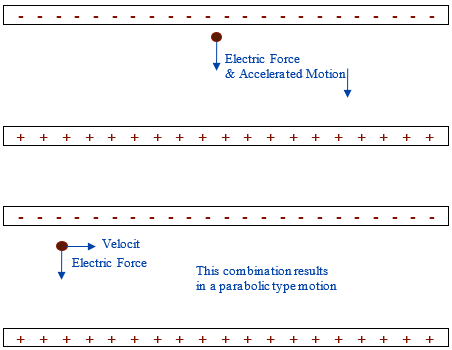
If the negative charge is stationary, then it will accelerate towards the positive plate using similar equations to what was used in vertical motion problems.

If the negative charge is moving at 90° to the direction of the electric field then, the motion of the negative charged object will be one that is parabolic using equations similar to what was used in the study of parabolic motion.

To analyze the motion of charged particles in a constant electric field, the electric force law is used in conjunction with the one or more of the accelerated motion or constant velocity equations. Expect to see combinations of the equations below used with this topic in future courses.

Four Kinematic Equations:

• [latex]\vec{d}=\dfrac{(\vec{v_i}+\vec{v_f})t}{2}[/latex]
• [latex]2\vec{a}\vec{d}=\vec{{v_f}^2}-\vec{{v_i}^2}[/latex]
• [latex]\vec{v_f}=\vec{v_i}+\vec{a}t[/latex]
• [latex]d=\vec{v_i}t+\dfrac{1}{2}\vec{a}t^2[/latex]

Electric Force:

[latex]{F}_{el}=q\vec{E}[/latex]

Constant Velocity:

[latex]\vec{v}=\dfrac{\vec{d}}{t}[/latex]

21.3 Energy, Momentum & Charged Particles

Equations Introduced or Used for this Section:

• [latex]\vec{J}=\Delta\vec{q}[/latex] where [latex]\vec{F}=m\Delta\vec{v}[/latex]
• [latex]E_k=\dfrac{1}{2}mv^2[/latex]
• [latex]\Delta \text{Energy}=\vec{F}\vec{d}\text{ cos ø}[/latex]
• [latex]\vec{F}_{el}=q\vec{E}[/latex]

In this section, we continue to explore the dynamics of charged particles moving through constant electric fields as changes in both their momentum and/or energy. The technological discoveries that resulted from applying the physics developed using a constant electric field are significant. Some of these are: the very first particle accelerators, the first radar and TV tubes, and evidence allowing for the measure of the charge and mass of both the electron and proton. Using the relationship between the change in kinetic energy and the energy change of charged particles inside uniform electric fields also helped in the development of solar panels for electricity and was critical to understanding the relationship between light, energy and charged particles. While deeper inspections into these relationships is only alluded to in this topic, it will be in the study of magnetism when combined with constant electric fields that the major discoveries that were first in providing scientists with a foundational understanding on the structural nature of atoms and molecules.

This section piggybacks on the original change in momentum and energy equations you encountered prior in Chapters 8, 9, 10 and 11: F t = m∆v and Fd cos ø = ∆ Energy. In most ways it is a review and extension of momentum and mechanical energy. The major difference is that now charged particles are affected by electric force and fields and the energy of these accelerated charged particles are defined by the voltage or potential difference they are accelerated or decelerated through. It is also the first Chapter where one pushes up against the limits of classical physics as it is possible with the apparatus and technologies used in this section to require the need of relativistic solutions to be able to understand and produce reliable results.

You will also notice that vector equations are freely used in scalar settings as direction is not needed to arrive at the desired solution. As a result, one can see the above equations written and used as the following:

• [latex]J=\Delta p\text{ where }F\,t=m\Delta v[/latex]
• [latex]E_k =\dfrac{1}{2}mv^2[/latex]
• [latex]\Delta \text{Energy}=\vec{F}\vec{d}\text{ cos ø}[/latex]
• [latex]\vec{F}_{el}=q\vec{E}[/latex]

This exploration of topics is important in your studies as it provides valuable insights that will be built upon in higher levels of physics in your studies of Atomic and Plasma physics. Please enjoy the fact that this is only the start of exploring some of the great adventures and discoveries that brought Classical Physics into the modern world of Relativistic and Quantum Physics.

Exercise Answers

21.1 Energy Change of Charge moving through a Uniform Electric Field

1.  3.5 × 10⁸ J
2. 0.225 J
3. 2.4 × 10⁻¹⁵ J or 15000 eV
4. 5000 eV or 5 keV

21.2 Uniform Electric Fields (Parallel Charged Plates)

1. 0.04 m
2. 630 V
3. 700 N/C
   1. 2000 N/C
   2. 2.0 × 10⁻⁵ N
   3. 10⁻⁶ J  or 1 µJ
   1. 50000 N/C
   2. 2000 V
   1. 90 V
   2. 6.0 × 10⁻⁸ N
   3. 3.0 × 10⁻⁹ J
   1. 5.0 × 10⁻¹⁰ N
   2. 5.0 × 10⁻¹² J
4. 285 V  (≈ 300 V)

21.3 Energy, Momentum & Charged Particles

1.  10⁻²⁴ Ns
2. 5.49 × 10⁻¹⁹ J or 3.43 eV
3. 0.51 m
   1. 5.47 × 10⁻²³ Ns South
   2. 5.47 × 10⁻¹⁷ N
4. 23.5 m
   1. 5.93 × 10⁶ m/s
   2. 183 000 eV or 0.183 MeV
   1. 0.0125 m
   2. 0.0125 m
   1. 7.64 × 10⁻²⁴ Ns
   2. 3.27 × 10⁻²² Ns
5. 9.4 × 10⁹ m/s…   around 31 time the speed of light (≈ 31 c)
6. 2.56 × 10⁻⁵ m   (or 25.6 µm)

21.4.1 The Millikan Oil Drop Experiment

1.  First estimated mass of the electron… m_e- = 1.22 × 10⁻³⁰ kg

21.4.2 An Early Cathode Ray Tube (CRT)

1. t = 1.1 × 10⁻⁸ s or 11 ns

21.4.3 Relativistic Charged Particles

1. v = 2.44 × 10⁸ m/s or 0.81c

Media Attributions

• “Andreas Cunaeus discovering the Leyden jar” from Augustin Privat Deschanel (1876) Elementary Treatise on Natural Philosophy is in the public domain.