16 Conservation of Heat Energy (First Law of Thermodynamics)

Resources

Equations Introduced and Used in this Topic:

  • [latex]\text{Heat}_{\text{Loss}}+ \text{Heat}_{\text{Gains}}= 0[/latex]
  • [latex]Q_{\text{loss}} + Q_{\text{gain}}= 0[/latex]
  • [latex]\Delta U=Q-W[/latex]

[latex]Q_i+E_{ki}+E_{pi}=E_{kf}+E_{pf}+Q_{f}[/latex] or [latex]\Delta Q+\Delta E_k+\Delta E_p=\text{ Constant}[/latex]

  • [latex]Q=mc\Delta T[/latex]
  • [latex]Q=\pm mL_f[/latex]
  • [latex]Q=\pm mL_v[/latex]
  • [latex]E_p=mgh[/latex]
  • [latex]E_k=\dfrac{1}{2}mv^2[/latex]
  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}[/latex]
  • [latex]\text{Efficiency}=\dfrac{\text{Output}}{\text{Input}}\times100\%[/latex]

Where…

  • [latex]∆U[/latex] is the Total Internal Energy of a System, measured in joules (J)
  • [latex]Q[/latex] is the Heat (energy), measured in joules (J)
  • [latex]L_v[/latex] is the Latent Heat of Vaporization, measured in joules/kilogram (J/kg)
  • [latex]L_f[/latex] is the Latent Heat of Fusion, measured in joules/kilogram (J/kg)
  • [latex]∆T[/latex] is the Change in Temperature (Tf – Ti), measured in Celsius (°C) or Kelvin (K)
  • [latex]c[/latex] is the specific heat constant, measured in joules/kilogram degrees Celsius (J/kg°C). Specific heat is found by experiment but has a rough value for specific temperature ranges.
  • [latex]E_p[/latex] is Potential Energy, measured in joules (J)
  • [latex]E_k[/latex] is Kinetic Energy, measured in joules (J)
  • [latex]m[/latex] is the Mass of the object, measured in kilograms (kg)
  • [latex]g[/latex] or [latex]a_g[/latex] is the Gravitational Field Strength, measured in metres per second squared (m/s2)
  • [latex]h[/latex] is the change in Vertical Height, measured in metres (m)
  • [latex]v[/latex] is the Speed of the object, measured in metres per second (m/s)
  • [latex]P[/latex] is the Power, measured in watts (W)
  • [latex]W[/latex] is Work, measured in joules (J)
  • [latex]t[/latex] is Time, measured in seconds (s)
  • [latex]∆\text{Energy}[/latex] is the change in a combination of Mechanical and Heat Energy forms
    ([latex]\Delta E_p = E_{pf}- E_{pi}[/latex], [latex]\Delta E_k=E_{kf}-E_{ki}[/latex] or [latex]\Delta Q=Q_f-Q_i[/latex]) and is measured in joules (J).
Specific Heat
Material Specific Heat Material Specific Heat
Aluminum 900 J/kg°C Lead 160 J/kg°C
Brass 384 J/kg°C Mercury 139 J/kg°C
Copper 390 J/kg°C Pyrex 837 J/kg°C
Ethanol 2400 J/kg°C Silver 235 J/kg°C
Glass 840 J/kg°C Steel 445 J/kg°C
Ice 2100 J/kg°C Steam 2020 J/kg°C
Iron 460 J/kg°C Water 4187 J/kg°C
Latent Heats of Fusion and Vaporization
Material Lf (J/kg) Lv (J/kg)
Water 3.34 × 105 2.26 × 106
Mercury 1.18 × 104 2.96 × 105
Ethyl Alcohol 1.05 × 105 8.54× 105
Nitrogen 2.55 × 104 1.99 × 105
Oxygen 1.38 × 104 2.13 × 105
Hydrogen 5.86 × 104 4.52 × 105
Helium 5.23 × 103 2 × 104
Fusion and Vaporization Temperatures
Material Tf (°C) Tv (°C)
Water 0 100
Mercury −38.8 356.7
Aluminum 660.3 2519
Nitrogen −210 −195.8
Oxygen −218.8 −183
Hydrogen −259.1 −252.9
Helium −272.2 −268.9

16.1 Conservation of Heat Energy

Equations Introduced or Used for this Section:

  • [latex]\text{Heat}_{\text{Loss}}+ \text{Heat}_{\text{Gains}}= 0[/latex]
  • [latex]Q_{\text{loss}} + Q_{\text{gain}}= 0[/latex]
  • [latex]Q=mc\Delta T[/latex]
  • [latex]Q=\pm mL_f[/latex]
  • [latex]Q=\pm mL_v[/latex]

The study of the movement of Heat Energy is called Thermodynamics.

The Field of Thermodynamics[1]

Article to Read: In praise of Lord Kelvin

Wikipedia describes the history of thermodynamics as:

“… a fundamental strand in the history of physics, the history of chemistry, and the history of science in general. Owing to the relevance of thermodynamics in much of science and technology, its history is finely woven with the developments of classical mechanics, quantum mechanics, magnetism, and chemical kinetics, to more distant applied fields such as meteorology, information theory, and biology (physiology), and to technological developments such as the steam engine, internal combustion engine, cryogenics and electricity generation. The development of thermodynamics both drove and was driven by atomic theory. It also, albeit in a subtle manner, motivated new directions in probability and statistics.”

Article to Read: The Historical Development of Thermodynamics

In the timespan between 1823 to 1882, research and study of this field both changed and unified previously disparate fields of study and helped to move away from philosophical conceptions of heat and energy as substances.[2] The breakthrough first came from the theory of the Conservation of Energy.  Four laws eventually came to be associated with the foundation of the field of thermodynamics, with the first law being an extension of the conservation of energy to include heat. Central to the development of these laws was that it was a form of mechanical energy.

The First Law of Thermodynamics is a variation of the Law of Conservation of Energy that is adapted for Thermodynamic Systems . It can be stated as follows: The total energy of an isolated system is constant, where energy can be transformed from one form to another but can be neither created or destroyed. In an equation this is written as:

Internal Energy of a System = Heat added to a System − Work done by the System

or…  [latex]\Delta U=Q-W[/latex]

One of the implications of this law is that it is impossible to create perpetual motion machines that will produce work with no input of any energy source. Perpetual motion machines are an impossibility.

The second and third laws of thermodynamics concern themselves with the phenomenon known as entropy.  Entropy was first introduced to describe the waste heat or energy loss from heat engines, and as such was related to the efficiency of mechanical devices in doing work. In 1865, this concept evolved into a concept of disorder, which related to the kinetic energy of particles in a system where eventually all particles will reach a state of high disorder and high entropy.  Recently entropy is being explained as “energy dispersal” of a system, specifically the spread of temperature throughout a system as a function of temperature.

Using this revision the Second Law of Thermodynamics is introduced as:

Energy naturally disperses from being concentrated to spreading out if it is not restrained from doing so.

In this setting, entropy is understood as looking at the process of energy change, such as the heat dissipated from a hot stove burner as it cools down, ice melting in a glass of water, air escaping from an inflated balloon or the continual erosion of mountains from steep to gentle slopes as racks break free, converting potential energy to kinetic energy, heat and work on what it falls onto. Prior to this change, the Second Law of Thermodynamics was taught as the sum of the entropies of the interacting thermodynamic systems’ increases.

The Third Law of Thermodynamics is defined as:

The entropy of a system will approach a constant as the system gets closer to Absolute Zero.

The third law  implies that it is impossible for any system to ever reach absolute zero.

The Fourth Law ended up being defined as the Zeroth Law of Thermodynamics. In this law, the concept of temperature is defined. Specifically:

If a body A and a body B are both in equilibrium with each other; then a body C that is in thermal equilibrium with body B will also be in equilibrium with body A and the temperature of body C is equal to the temperature of body A.

A quick interpretation of this is: if we place a thermometer in a cup of boiling water, it will rise in temperature until it reads 100°C.  At this point both the thermometer and boiling water are in thermal equilibrium with each other.  If this thermometer is then placed in a second cup of boiling water and it continues to read 100°C then both cups of boiling water and the thermometer are in thermal equilibrium with each other.

Or, if a thermometer reads the same temperature for two different systems, then both of these systems will be in thermal equilibrium with each other.  If these two systems were then to be placed in contact with each other, there would be no heat energy exchanged between them.

Example 16.1.1

454 g of water at a temperature of 98.0 °C is poured into a 750 g glass container (specific heat 840 J/kg°C).  If the initial temperature of the glass is 21.0 °C find its final temperature.

Solution

Data:

Qloss Data Qgain Data
[latex]m[/latex] = 0.454 kg [latex]m[/latex] = 0.750 kg
[latex]c_{\text{water}}[/latex] = 4187 J/kg°C [latex]c_{\text{glass}}[/latex] = 840 J/kg°C
[latex]T_f[/latex] = Find [latex]T_i[/latex] = 21.0°C
[latex]T_i[/latex] = 98 °C

Solution:

  • [latex]Q_{\text{loss}} + Q_{\text{gain}}= 0[/latex]
  • [latex]mc\Delta T+mc\Delta T=0[/latex]
  • [latex]mc(T_f-T_i)+mc(T_f-T_i)=0[/latex]
  • [latex](0.454\text{ kg})(4187\text{ J/kg°C})(T_f-98.0\text{°C}) + (0.750\text{ kg})(840\text{ J/kg°C})(T_f-21.0\text{°C}) = 0[/latex]
  • [latex](1900\text{ J/°C})T_f-186\;300\text{ J}+(630\text{ J/°C})T_f-13\;200\text{ J} = 0[/latex]
  • [latex](2530\text{ J/°C})T_f-199\;500\text{ J}=0[/latex]
  • [latex](2530\text{ J/°C})T_f=199\;500\text{ J}[/latex]
  • [latex]T_f=199\;500\text{ J}\div 2530\text{ J/°C}[/latex]
  • [latex]T_f=78.8\text{°C}[/latex]

Example 16.1.2

What mass of ice at its melting point would be needed to lower the temperature of 1.5 kg of water initially at 75°C to 2.5°C?

Solution

Data:

  • [latex]Q_{\text{loss}}[/latex]…
    • [latex]m[/latex] = 1.5 kg
    • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
    • [latex]T_i[/latex] = 75 °C
    • [latex]T_f[/latex] = 2.5 °C

Solution:

  • [latex]Q_{\text{loss}} + Q_{\text{gain}}= 0[/latex]
  • [latex](mL_f+mc\Delta T)+mc\Delta T=0[/latex]
  • [latex][mL_f+mc(T_f-T_i)]+mc(T_f-T_i)=0[/latex]
  • [latex]m(3.34\times10^5\text{ J/kg}) + m(4187\text{ J/kg°C})(2.5\text{ °C}-0\text{°C})+(1.5\text{ kg})(4187\text{ J/kg°C})(2.5\text{ °C}-75\text{ °C})=0[/latex]

Factor out the common unknown mass and reduce…

Data:

  • [latex]Q_{\text{gain}}[/latex]…
    • [latex]m[/latex] = Find
    • [latex]L_f[/latex] = 3.34 × 105
    • [latex]T_f[/latex] = 2.5 °C
    • [latex]T_i[/latex] = 0 °C

Solution:

  • [latex]m(3.44\times 105\text{ J/kg})-455\;300\text{ J}=0[/latex]
  • [latex]m(3.44\times 105\text{ J/kg})=455\;300\text{ J}[/latex]
  • [latex]m=455\;300\text{ J}\div 3.44\times 10^5\text{ J/kg}[/latex]
  • [latex]m=1.32\text{ kg}(\approx1.3\text{ kg})[/latex]

Exercise 16.1

  1. If 0.20 kg of water at 85.5 °C is mixed with 0.54 kg of water at 15.5 °C what will be the resulting temperature of this mixture?
  2. What mass of water at a temperature of 2.5 °C is added to 15 g of ethanol (specific heat 2490 J/kg°C) at 18 °C, if this mixture reaches a final temperature of 6.0 °C?
  3. 515 g of water at a temperature of 65.5 °C is poured into a 655 g glass container (specific heat 840 J/kg°C). If the initial temperature of the glass is 20.0 °C, find its final temperature.
  4. 1.00 litres of water at a temperature of 95.0°C is poured into a 6.0 kg lead container at 16.0°C. To what temperature does the lead container rise?
  5. A 30 gram spoon (20°C) is placed into a styrofoam cup containing 300 grams of hot coffee (85°C). What will be the final temperature of the coffee and the spoon?  (Ignore the heat lost to warming the styrofoam cup).
  6. If one pours 2 large 20 litre pails (total mass = 40 kg) of boiling water into a tub of water containing 5 – 20 litre pails (total mass = 100 kg) of fresh stream water initially at 14 °C, how hot would the resulting bath water be? (Assume the energy lost to heating the tub is insignificant.)
  7. What mass of ice at its melting point would be needed to lower the temperature of 0.75 kg of water initially at 95 °C to 3.5 °C?
  8. A copper calorimeter (specific heat of 390 J/kg°C) has a mass of 155 g and contains 95.5 g of water all at 62.4 °C. What mass of ice at 0 °C is needed to cool this calorimeter and water down to 16.5 °C?
  9. What is the mass of steam at 100 °C that would need to be combined with a 1.50 kg block of ice at 0.0 °C to convert it to water at 21.5 °C?
  10. A child puts one 40 gram ice cube at 0 °C into a bowl containing 350 grams of chicken noodle soup at 92 °C. What should be the final temperature of the soup from adding the ice cube?  (Ignore the heat capacity of the bowl and use the specific heat of water for the soup.)
  11. 2.0 kg of ice at 0°C is dumped into a bathtub holding 150 litres of water at 18°C. What is the final equilibrium temperature of this mixture?
  12. A child mixes 100 ml of water at 98°C with 75 ml of water at 30°C and a 50 gram ice cube at 0°C. What is the final equilibrium temperature of this mixture?

16.2 Conservation of Heat & Mechanical

Article to Read: Traveling to the Sun – Why won’t Parker Solar Probe melt?

Equations Introduced or Used for this Section:

Conservation of Energy:

  • Energy Loss + Energy Gains = 0
  • [latex]Q_i+E_{ki}+E_{pi}=E_{kf}+E_{pf}+Q_f[/latex]

Energy Forms:

  • [latex]Q=mc\Delta T[/latex]
  • [latex]Q=\pm mL_f[/latex]
  • [latex]Q=\pm mL_v[/latex]
  • [latex]E_p=mgh[/latex]
  • [latex]E_k=\dfrac{1}{2}mv^2[/latex]

Power& Efficiency:

  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}[/latex]
  • [latex]\text{Efficiency}=\dfrac{\text{Output}}{\text{Input}}\times100\%[/latex]

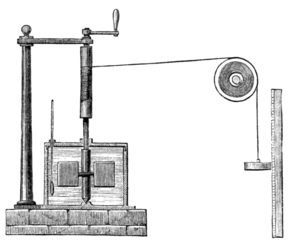Since heat is a form of energy, just like kinetic and potential energy, one is able to expand the Conservation of Mechanical Energy law to include heat energy. The caveat for this relationship is that Heat can only be converted between the Potential, Kinetic and Heat forms and that the system is isolated. Count Rumford’s 1797 demonstration that frictional forces could be used as a way to heat water outside of fire was a watershed demonstration that challenged the accepted caloric theory of heat. By the 1850s, several prominent scientists had started to equate the concept of work to heat. In 1845, James Joule, through his experiments using the apparatus to the right, quantified the amount of mechanical work it took to raise the temperature of a defined mass of water, specifically, it took 4155 J to raise 1 kg of water 1 °C. While Joule is credited with the quantification between heat and mechanical energy, a bitter controversy erupted between Julius Robert von Mayer and James Joule over whose idea was the foundation of this relationship. Their very public battle raged for close to two decades, but in the end James Joule was given credit for claiming priority in the discovery of the relationship between work and heat.

Example 16.2.1

What would be the change in temperature of water that falls over a 120 m waterfall?

Solution

Data:

  • [latex]m[/latex] = common
  • [latex]g[/latex] = 9.80 m/s2
  • [latex]h[/latex] = 120 m
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
  • [latex]\Delta T[/latex] = Find

All of the initial potential energy converts to heat, therefore…

  • [latex]E_{pi}=\Delta Q[/latex]
  • [latex]mg\Delta h=mc\Delta T[/latex]… (cancel the common mass)
  • Therefore… [latex]g\Delta h=c\Delta T[/latex]
  • [latex](4187\text{ J/kg°C})\Delta T=(9.80\text{ m/s}^2)(120\text{ m})[/latex]
  • [latex]\Delta T=1176\text{ J}\div(4187\text{ J/kg°C})[/latex]
  • [latex]\Delta T=0.28\text{°C}[/latex]

Example 16.2.2

What vertical distance does water have to fall to raise its temperature by 0.50°C?

Solution

Data:

  • [latex]m[/latex] = common
  • [latex]g[/latex] = 9.80 m/s2
  • [latex]\Delta h[/latex] = Find
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
  • [latex]\Delta T[/latex] = 0.50°C

All of the initial potential energy converts to heat, therefore…

  • [latex]E_{pi}=\Delta Q[/latex]
  • [latex]mg\Delta h=mc\Delta T[/latex]… (cancel the common mass)
  • Therefore… [latex]g\Delta h=c\Delta T[/latex]
  • [latex](4187\text{ J/kg°C})(0.50\text{°C})=(9.80\text{ m/s}^2)\Delta h[/latex]
  • [latex]\Delta h=2094\text{ J/kg}\div(9.80\text{ m/s}^2)\text{ or }214\text{ m}[/latex]
  • [latex]\Delta h=214\text{ m}(\approx210\text{ m})[/latex]

Example 16.2.3

A 1450 kg minivan is driven down a mountain road, maintaining a constant speed of 90 km/h by applying the brakes for the descent. Over what vertical drop would the 42 kg of iron brake shoes increase in temperature by 500°C if all potential energy is absorbed by the brakes and no heat dissipated?

Solution

Data:

  • [latex]m_{\text{iron}}[/latex] = 42 kg
  • [latex]m_{\text{minivan}}[/latex] = 1450 kg
  • [latex]g[/latex] = 9.80 m/s2
  • [latex]\Delta h[/latex] = Find
  • [latex]c_{\text{iron}}[/latex] = 460 J/kg°C
  • [latex]\Delta T[/latex] = 500°C

All of the initial potential energy converts to heat, therefore…

  • [latex]E_{pi}=\Delta Q[/latex]
  • [latex]mg\Delta h=mc\Delta T[/latex]… (cancel the common mass)
  • [latex](1450\text{ kg})(9.80\text{ m/s}^2)\Delta h=(42\text{ kg})(460\text{ J/kg°C})(500\text{°C})[/latex]
  • [latex]\Delta h=(42\text{ kg})(460\text{ J/kg°C})(500\text{°C})\div(1450\text{ kg})(9.80\text{ m/s}^2)[/latex]
  • [latex]\Delta h=680\text{ m}[/latex]

Example 16.2.4

Suppose that a 150 kg block of ice at 0°C is slid across a rough wooden floor for a distance of 12 m.  What is the µk between these two surfaces if 8.0 g of ice melts?

Solution

Recall, [latex]W = F d \cos ø[/latex] which for friction means that…

[latex]W=(\mu_{k}mg\text{ cos ø})d=\Delta Q[/latex]

Now…

  • [latex]µ_k[/latex] = Find
  • [latex]m_{\text{ice}}[/latex] = 150 kg
  • [latex]d[/latex] = 12 m
  • [latex]g[/latex] = 9.80 m/s2
  • [latex]m_{\text{melt}}[/latex] = 0.0080 kg
  • [latex]L_f[/latex] = 3.34 × 105 J/kg

Solution:

  • [latex]F_fd=\Delta Q[/latex]
  • [latex]\mu_{k}mg\text{ cos ø})d=\Delta Q[/latex]
  • [latex]\mu_k(150\text{ kg})(9.80\text{ m/s}^2\text{cos 0°}(12\text{ m})=(0.0080\text{ kg})(3.34\times10^5\text{ J/kg})[/latex]
  • [latex]\mu_k(17640\text{ J})=2672\text{ J}[/latex]
  • [latex]\mu_k=2672\text{ J}\div 17640\text{ J}[/latex]
  • [latex]\mu_k=0.15[/latex]

Exercise 16.2

  1. What would be the change in temperature of water that falls over a 350 m waterfall?
  2. What vertical distance does water have to fall to raise its temperature by 1.0°C?
  3. A 1200 kg car traveling at 108 km/h brakes to a full stop in 8.0s. If all kinetic energy of this stop is absorbed by the 12 kg of iron brake shoes, what should be their increase in temperature?
  4. A 2400 kg truck is driven down a mountain road, maintaining a constant speed of 90 km/h by applying the brakes for the descent. Over what vertical drop would the 32 kg of iron brake shoes increase in temperature by 500°C if all potential energy is absorbed by the brakes and no heat dissipates?

16.3 Heat, Energy & Power

Research News: University of Zurich (April 19, 2019) Thermodynamic magic enables cooling without energy consumption

Equations Introduced or Used for this Section:

  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}[/latex]
  • [latex]\text{Efficiency}=\dfrac{\text{Output}}{\text{Input}}\times100\%[/latex]
  • [latex]Q=mc\Delta T[/latex]
  • [latex]Q=\pm mL_f[/latex]
  • [latex]Q=\pm mL_v[/latex]
  • [latex]E_p=mgh[/latex]
  • [latex]E_k=\dfrac{1}{2}mv^2[/latex]

Measurements of power and efficiency are quantified in similar ways to the measure of each in different fields. Power, as defined in Chapter 11, is the measure of the rate at which work is done. In this section, the work done expands from measuring the changes in mechanical energy to include heat energy. As such the measure of power can be quantified as:

[latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}=\dfrac{\Delta E_p+\Delta E_k+\Delta Q}{t}[/latex]

One of the distinctions in this quantification is that we now have a measure for the efficiency of these energy changes, specifically how much energy is useful in doing the work we wish to do. In this manner, we look at the ratio of power inputs and outputs, which is generally converted to a percentage for easier comparison. Efficiency in this manner is quantified as:

[latex]\text{Efficiency}=\dfrac{\text{Output}}{\text{Input}}\times100\%[/latex]

The input/output measures in this quantification can be used to explore the efficiencies of energy, work and power, which in all cases look at what we get out as useful or useable outputs compared to what we input.  Efficiency is unit-less and is converted from the percentage (useful to explain) to a decimal (useful for calculations) as needed.

For Instance: Consider a 1200 W engine that is 80% efficient. It will produce (0.80)(1200 W) or 960 W of useful power to do work. Also 20% or (0.20) (1200 W) or 240 W of the power of this engine is wasted.

Example 16.3.1

A 5.00 kg block of ice at 0.0 °C is just melted using a blowtorch by supplying heat at a uniform rate for 10 min. At what rate in joules per second (or watts) is heat being supplied?

Solution

Data:

  • [latex]P[/latex] = Find
  • [latex]t[/latex] = 10 min or 10 (60 s)
  • [latex]m[/latex] = 5.00 kg
  • [latex]L_f[/latex] = 3.34 × 105 J/kg

Solution:

  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}=\dfrac{mL_f}{t}[/latex]
  • [latex]P=\dfrac{(5.00\text{ kg})(3.34\times10^5\text{ J/kg})}{10(60\text{ s})}[/latex]
  • P = 2780 W (≈ 2800 W)

Example 16.3.2

At what rate is a refrigerator absorbing heat if 454 g of water at 30 °C freezes in 45 min?

Solution

Data:

  • [latex]P[/latex] = Find
  • [latex]t[/latex] = 45 min or 45(60 s)
  • [latex]m[/latex] = 0.454 kg
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
  • [latex]L_f[/latex] = 3.34 × 105 J/kg
  • [latex]T_f[/latex] = 0°C
  • [latex]T_i[/latex] = 30°C

Solution:

  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}=-\dfrac{mL_f+mc\Delta T}{t}[/latex]
  • [latex]P=-\dfrac{(0.454\text{ kg})(3.34\times10^5\text{ J/kg})+(0.454\text{ kg})(4187\text{ J/kg°C})(0\text{°C}-30\text{°C})}{45(60\text{ s})}[/latex]
  • [latex]P=-\dfrac{151\;600\text{ J}-57\;000\text{ J}}{2700\text{ s}}[/latex]
  • [latex]P[/latex] = − 77 W or it is absorbing heat at the rate of 77 W

Example 16.3.3

The heater filament in an electric kettle can supply heat at the rate of 1400 W.  How much time would it take to boil away 454 g of water at an initial temperature of 4.0°C?

Solution

Data:

  • [latex]P[/latex] = 1400 W
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
  • [latex]T_i[/latex] = 4.0°C
  • [latex]T_f[/latex] = 100°C
  • [latex]L_v[/latex] = 2.26 × 106 J/kg

Solution:

  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}=\dfrac{mc\Delta T+mL_v}{t}[/latex]
  • [latex]1400\text{ W}=\dfrac{(0.454\text{ kg})(4187\text{ J/kg°C})(100\text{°C}-4.0\text{°C})+(0.454\text{ kg})(2.26\times10^6\text{ J/kg})}{t}[/latex]
  • [latex]t=-\dfrac{182\;500\text{ J}+1\;030\;600\text{ J}}{1400\text{ W}}[/latex]
  • [latex]t[/latex] = 866 s or 14 minutes 26 seconds

Example 16.3.4

A stainless steel[3] kettle (mass 0.525 kg) contains 2.0 kg of water.  If 42.0% of the electricity used is converted into heating the kettle and water, then how much total electric energy is required to raise the temperature from 21.0 °C to 98.0 °C?

Solution

Data:

  • [latex]P[/latex] = 1400 W
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
  • [latex]m_{\text{water}}[/latex] = 2.0 kg
  • [latex]c_{\text{steel}}[/latex] = 445 J/kg°C
  • [latex]m_{\text{steel}}[/latex] = 0.525 kg
  • [latex]T_f[/latex] = 98.0°C
  • [latex]T_i[/latex] = 21.0°C

Solution:

  • Energy = (2.0 kg)(4187 J/kg°C)(98.0°C − 21.0°C) + (0.525 kg)(445 J/kg°C)(98.0°C − 21.0°C)
  • Energy = 644800 J + 18000 J
  • Energy = 662800 J

Since this is only 42% efficient, the electrical energy is:

  • [latex]\text{Efficiency}=\dfrac{\text{Output}}{\text{Input}}\times100\%[/latex]
  • [latex]42\%=\dfrac{662\;800\text{ J}}{E_{\text{input}}}\times 100\%[/latex]
  • [latex]E_{\text{input}}=\dfrac{662\;800\text{ J}}{0.42}[/latex] or 1580000 J

Example 16.3.5

An electric kettle rated at 1.8 kW takes 1 minute 50 seconds to boil 0.454 kg of water initially at 21 °C. Find this kettle’s efficiency.

Solution

Data:

  • [latex]P_{\text{actual}}[/latex] = Find
  • [latex]P_{\text{rated}}[/latex] = 1800 W
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C
  • [latex]L_v[/latex] = 2.26 × 106 J/kg
  • [latex]t[/latex] = 1 min 50 s (=110 s)
  • [latex]m_{\text{water}}[/latex] = 0.454 kg
  • [latex]T_f[/latex] = 100°C
  • [latex]T_i[/latex] = 21.0°C
  • Efficiency = Find

First, find the Actual Power realized

  • [latex]\text{Power }(P)=\dfrac{W}{t}=\dfrac{\Delta \text{Energy}}{t}=\dfrac{mc\Delta T}{t}[/latex]
  • [latex]P=\dfrac{(0.454\text{ kg})(4187\text{ J/kg°C})(100\text{°C}-21.0\text{°C})}{110\text{ s}}[/latex]
  • [latex]P[/latex] = 1365 W

Example 16.3.6

In a ballistics testing centre, forensic technicians are firing a 9 mm handgun into a gel to identify rifling marks on the fired bullet. If this bullet has a mass of 7.5 g and a muzzle velocity of 380 m/s, how much should the bullet heat up if 60% of its kinetic energy is converted to heating the bullet?  The specific heat of lead = 129 J/kg°C.

Solution

Data:

  • [latex]m_{\text{bullet}}[/latex] = 0.0075 kg
  • [latex]c_{\text{lead}}[/latex] = 460 J/kg°C
  • [latex]\Delta T[/latex] = Find
  • [latex]V_f[/latex] = 0 m/s
  • [latex]V_i[/latex] = 380 m/s

60% of the initial kinetic energy converts to to heat, therefore…

  • [latex]E_{ki}=\Delta Q[/latex]
  • [latex]\dfrac{1}{2}{mv_i}^2=mc\Delta T[/latex]… (cancel the common mass)
  • [latex]\dfrac{1}{2}{v_i}^2=c\Delta T[/latex]
  • [latex](0.60) \dfrac{1}{2}(380\text{ m/s})^2=(129\text{ J/kg°C})\Delta T[/latex]
  • [latex]\Delta T=4.332\times 10$4\text{ J}\div (129\text{ J/kg°C})[/latex]
  • [latex]\Delta T=336\text{°C}[/latex]

Exercise 16.3

  1. An insulated thermos contains 3.0 litres of water at 45 °C.  At what rate (in joules per second) is this water losing heat if it cools to 38 °C over an 8.0 h period?
  2. An immersion heater can supply heat at the rate of 480 J/s. How much time will it take to boil away 0.125 kg of water at 26.5 °C?
  3. A 2.00 kg block of ice at 0 °C is just melted by supplying heat at uniform rate for 15 min. At what rate in joules per second (or watts) is heat being supplied?
  4. At what rate is a refrigerator absorbing heat if 2.15 kg of water at 21.5 °C freezes in 2.00 h?
  5. A 1.0 kW aluminum electric kettle (mass 450 g) is used to heat 0.85 litres of water from 15 °C to boiling. If the specific heat of aluminum is 900 J/kg°C how long does it take this water to begin boiling?  Assume that all the electricity used is converted to heat.
  6. A bathtub contains 90 litres of water at 70°C which cools to 40°C in 30 minutes. What is the average rate of heat loss of this tub of water?
  7. An electric kettle rated at 2.5 kW takes 1 minute 15 seconds to boil 0.35 kg of water initially at 18 °C. Find this kettle’s efficiency.
  8. A heating oil was found to release 4.15 × 107 J of energy for each kg burned in air.  If this oil is used to heat 245 litres of water from 12 °C to 68 °C and this conversion is 62% efficient, what mass of heating oil is required?
  9. A piece of copper (specific heat of 390 J/kg°C) is dropped from a height of 255 m. If 55% of its kinetic energy (upon impact with the ground) heats up this copper, what will be the rise in its temperature?
  10. A stainless steel kettle (mass 0.525 kg) contains 0.155 kg of water. If 65.0% of the electricity used is converted into heat how much energy is required to raise the temperature of this kettle and water from 12.0 °C to 96.0 °C?  Specific heat of stainless steel is 445 J/kg°C.

Exercise 16.4.1: WAIS

The WAIS (West Antarctic Ice Shelf) is capable of raising the global sea level around 4.8 metres.

  1. What volume of water is this?  (Earth’s Ocean Surface Area = 3.61 × 1011 m2)
  2. How much ice does this represent?  (Ice has a density of 916.7 kg/m3)P
  3. How much energy is required to melt this ice?  (Assume a temperature of − 45 °C)
  4. By how much could it lower the average ocean temperature?  (Mass of ocean is about 1.4 × 1021 kg…  Use the average upper ocean (4% of the total ocean volume) to calculate the change in temperature (around 17°C)

Article to Read: Voosen, P. (2018) Discovery of recent Antarctic ice sheet collapse raises fears of a new global flood

Exercise16.4.2: The Heat Energy of the Oceans

If the area of the ocean covers roughly 361 million square kilometres (3.61 × 1012 m2):

  1. How much energy must be radiated to freeze the top 300 m?  Global average of the surface is 17°C.
  2. How many days of a complete blockage of sunlight would this take?
  3. Google Search “time to freeze Earth with no sunlight” Why would it take longer than this calculated time?

Exercise Answers

16.1 Conservation of Heat Energy

  1. 34.4 °C
  2. 30.6 g
  3. 56.2 °C
  4. 82.7 °C
  5. 84.3 °C
  6. 38.6 °C
  7. 0.82 kg
  8. 0.0524 kg
  9. 0.247 kg
  10. 74.4 °C
  11. 16.7 °C
  12. 35.8 °C

16.2 Heat & Mechanical Energy

  1. 0.82 °C
  2. 430 m
  3. 97.8 °C
  4. 313 m drop

16.3 Heat, Energy, Power & Efficiency

  1. 3.05 J/s or W
  2. 670 s
  3. 742 J/s or W
  4. − 127 J/s or W
  5. 5.6 minutes
  6. − 6280 J/s
  7. 64%
  8. 2.2 kg
  9. 3.5 °C
  10. 1.14 kJ

16.4.1 WAIS

  1.  1.73 × 1012 m3
  2. 1.59 × 1015 kg
  3. 6.8 × 1020 J
  4. 0.0033 °C  (Insignificant)

16.4.2 Heat Energy of the Oceans

  1. 4.39 × 1023 J
  2. 42.2 days of no sunlight
  1. The 42.2 days that you calculated in question two is incorrect. More often a time of 400 days is quoted, for example in this article If the Sun Went Out, How Long Before We’d Freeze? from the Washington City Paper, and that is do the insulating properties of the ice. The article If The Sun Went Out, How Long Would Life On Earth Survive? from Popsci explains “Within a week, the average global surface temperature would drop below 0°F. In a year, it would dip to –100°. The top layers of the oceans would freeze over, but in an apocalyptic irony, that ice would insulate the deep water below and prevent the oceans from freezing solid for hundreds of thousands of years.”

Media Attributions

  1. Thermodynamics comes from the Latin, meaning the movement of heat, and was first used by William Thomson, a.k.a. Lord Kelvin (1824-1907) ↵
  2. Previous theories of heat were quite elegant and were successful in explaining a great number of natural phenomena such as the gas laws and heat transfer. ↵
  3. Specific heat of stainless steel is 445 J/kg°C ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Foundations of Physics Copyright © by Terrance Berg is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book