Equations Introduced and Used in this Topic:

• [latex]I = \dfrac{q}{t}[/latex] or [latex]q = It[/latex]
• [latex]V = IR[/latex]

[latex]P=\dfrac{\text{work}}{t}=\dfrac{\Delta E}{t}[/latex]

Where…

• [latex]I[/latex] is the Electric Current, measured in amperes or amps (A)
• [latex]t[/latex] is the Time, measured in seconds (s)
• [latex]∆E[/latex] is the Energy, measured in joules (J)
• [latex]P[/latex] is the Power, measured in watts (W)
• [latex]V[/latex] is the voltage, measured in volts (V)
• [latex]R[/latex] is the Resistance, measured in ohms (Ω)
• [latex]W[/latex] is the work, measured in joules (J)
• [latex]q[/latex] is the Charge, measured in coulombs (C)

The next two topics in this text/workbook expand from the study of stationary charges (static electricity) to the continuous movement of electric charge (electric current).  Before the 1800s, static charge devices could only build up charge through the use of the Leyden Jar and the discharge of the stored charge tended to be disappointingly brief.  In 1800, Alessandro Volta (1745-1827) created the battery by stacking alternating pieces of silver and zinc metal discs, separated by moistened salt water or lye-soaked pieces of cardboard and leather.

Volta’s idea to use two dissimilar metals separated by an acidic blotter originated from an observation by his friend Luigi Galvani (1737-1798). Galvani was investigating medical electricity, then a growing area of interest, in an attempt to find the effects of electricity on the human body. The observation that caught Volta’s attention was Galvani’s dissection of a frog’s leg using a statically charged iron metal scalpel that sparked on the exposed sciatic nerve of the frog’s leg, causing it to jump. At this moment, Galvani discovered bio-electricity, which has evolved to its current field as electrophysiology. Volta originally agreed with Galvani’s belief that he had discovered animal electricity. However, Galvani soon turned his attention to the dissimilar metals used in his dissection, leading led him to create the first apparatus capable of producing a constant flow of electric charge.

22.1 Electric Current & Ohm’s Law

Equations Introduced or Used for this Section:

• [latex]I = \dfrac{q}{t}\text{ or }q = I t[/latex]
• [latex]V = IR[/latex]

[latex]q=(\pm1.602\times 10^{−19}\text{ C)(number of electrons/protons)}[/latex]

Electric Current (I) is the measure of the amount of charge that flows past a point in a conductor in a measured amount of time.  The units of measure are named after André-Marie Ampère (1775-1836), a French mathematician and physicist who is considered to have founded the study of classical electromagnetism, or classical electrodynamics, which is the study of the interactions between electric charges, or current and magnetic phenomena.

While the explosion of small, piecemeal discoveries about the nature of electricity began to untangle the mysteries of electric charge and the movement of it, the first to notice a link between electric current and magnetism was Hans Christian Ørsted (1777-1851). In 1820, Ørsted noticed the deflection of a compass needle as he switched off and on the electric current while giving a lecture.

News of Ørsted’s discovery encouraged Ampère to devote his attention to understanding the link between the flow of electric charge and magnetism. Ampère’s work established the first definition of electric current, which he defined as a “circulation of electric fluid in a closed circuit”.

The official measure of electric current as the ampere was established in 1881 at the International Exposition of Electricity, along with the other standard units of measure, specifically the coulomb, volt, ohm and watt.  The first official definition of electric current was defined as either the attractive or repulsive force of exactly 2.0 × 10⁻⁷ N that would exist between two parallel straight conductors separated by a distance of exactly 1 metre in a vacuum.

The measure of a coulomb of charge was obtained from extending the definition of the ampere^[1], specifically:

One coulomb of charge is the quantity of electric charge carried in one second by a current of one ampere.

Equating this relationship, you will encounter the equation:

[latex]I = \dfrac{q}{t}[/latex] or [latex]q = It[/latex]

with the units of Electric current being measured in amperes (A) or coulombs/second (C/S) and charge being measured in coulombs (C).

Ampère’s work is the foundation of Maxwell’s equations, which allowed scientists to “quantify 99.99% of the physical processes that humans experience, including touch, taste, sight and the neurological process of thinking itself.”^[2] Maxwell’s work later became the foundation of understanding how light was a form of an electromagnetic wave and, by extension, radio, television, radar, cell phones, computers and many other things.

Ohm’s Law is named after its discoverer, Georg Simon Ohm (1787-1854), who derived an equation that related electric current, resistance and voltage for simple circuits. Ohm managed to do this using a galvanometer and voltaic pile in an age where no standardization of electrical output and measurement of electric current existed. The equipment available for use in his age varied from set-up to set-up, since all pieces of equipment were generally made by hand by the experimenter or his assistant. Despite these variations, Ohm was able to gather enough evidence to support his theory of factors affecting the amount of electric current that would flow in a simple circuit.

Critical response to Ohm’s published work on this subject was quite hostile.  His works were called a “web of naked fancies”, and the German Minister at that time declared about Ohm that “a professor who preached such heresies was unworthy to teach science”.  Popular opinion held that experimentation was unnecessary to an understanding of the ordered structure of nature, and scientific truths could be deduced through reasoning alone. Ohm was sacked from his job as a high school teacher and remained in poverty for nearly two decades before his work was recognized as important. He was then appointed to a professorship at the University of Munich.

Ohm’s Law is an empirical law, meaning a generalization resulting from multiple experiments showing that the current is approximately proportional to the voltage across a conductor. The challenge is that this equation does not hold up for some high voltages across some conductors and will not work at all for some materials at all under low voltages.

The equation that garnered Ohm both fame and disdain is currently written as:

[latex]V=IR[/latex]

Where…

• [latex]V[/latex] is the voltage or the potential difference measured in volts (V)
• [latex]I[/latex] is the electric current that flows through the conductor measured in amperes (A)
• [latex]R[/latex] is the resistance of the conductor measured in ohms (Ω)

The following examples are concerned with electric current and Ohm’s Law.

22.2 Electric Power

Equations Introduced or Used for this Section:

• [latex]P=\dfrac{\text{work}}{t}=\dfrac{\Delta E}{t}[/latex]
• [latex]P=IV=I^2R=\dfrac{V^2}{R}[/latex]
• [latex]V=IR[/latex]
• [latex]W=\Delta E=qV\text{ or }q\vec{E}\vec{D}[/latex]

Electrical Power (P), like mechanical power, is defined as the rate at which work is done. The units of measure of Power is watts (W) where 1 watt is equivalent to the rate of 1 joule/second. There are two different types of electricity production, the first being Direct Current (DC) which is a constant flow of electric charge throughout a circuit, such as the charge caused by connection to a battery source related to Volta’s original voltaic pile. The second type is that of an alternating current which at the simplest level is created by rotating a wire coil inside a magnetic field. This second type is the most common one to be globally produced and consumed where electric current alternates in direction and in varying strength and is termed Alternating Current (AC). In North America, electric current reverses itself 60 times a second (60 Hertz or 60 Hz) and carries an average voltage of 120 volts. In reality the peak voltage coming from a 120 AC circuit varies between ±170 V and has a technical name called the “root mean square” (RMS). To calculate the peak voltage of any AC circuit using the RMS, multiply the average voltage by the square root of 2, or the peak voltage by the average 0.707.

The image below shows a graph of the sinusoidal nature of the AC current. When one is working with AC circuitry, one generally works with the average voltage of the circuit, which allows one to use the Power Law equation of linear load resistive circuits.

The power law equation takes the following form:

[latex]P=IV=I^2R=\dfrac{V^2}{R}[/latex]

Where…

• [latex]P[/latex] is the average power measured in watts (W)
• [latex]I[/latex] is the average electric current measured in amperes (A)
• [latex]V[/latex] is the potential difference or the voltage of the circuit measured in volts (V)
• [latex]R[/latex] is the resistance of the circuit measured in ohms (Ω)

This equation is derived from Joule’s Law. In 1840, James Joule discovered that the rate at which the resistivity of a circuit converts electricity into heat energy is proportional to the electrical resistance of the wire and the square of the current. Quantitatively, this is written as follows:

[latex]P=I^2R[/latex]

Combining this with Ohm’s Law: [latex]V = IR[/latex]  (or [latex]I = \dfrac{V}{R}[/latex] & [latex]R = \dfrac{V}{I}[/latex]), one is able to generate the entire equation as shown above through simple substitution.  Also, one often can see the power law equation shown as a wheel illustration in some form similar to the image at the beginning of this topic.

One of the interesting historical spin-offs of early research into electric power stems Luigi Galvani’s 1771 discovery that bio-electricity was the source causing muscles to move. This discovery resulted in the first medical attempts to revive and/or resuscitate people who had died or drowned. These attempts are recorded in medical journals of the time. In addition, contemporary novelists began to incorporate electric power in science fiction stories.

In the 1819 novel, Frankenstein; or, The Modern Prometheus, Mary Shelley created a fictional character who served as a prototype for literary monsters created using electricity. Subsequent authors, including Jules Verne, Edmond Hamilton, E.E. Doc Smith, John w. Campbell and H.G. Wells, incorporated electric power in their writing to create both heroes and villains wielding immense power.  In many ways, the mystique arising from electric power continues in the celebrity status of Nicholas Tesla and Thomas Edison as having changed the world through their mastery of the use and applications of electric power.

22.3 Electric Power and Energy Storage

Equations Introduced or Used for this Section:

• [latex]P=\dfrac{\text{work}}{t}=\dfrac{\Delta E}{t}[/latex]
• [latex]P=IV=I^2R=\dfrac{V^2}{R}[/latex]
• [latex]I = \dfrac{q}{t}[/latex] or [latex]q=It[/latex]
• [latex]W=\Delta E=P\,t =(IV)t[/latex]

Unit Conversions Used for this Topic:

1 kilowatt-hour (kWh)^[3]  =  3.6 megajoules  (MJ)

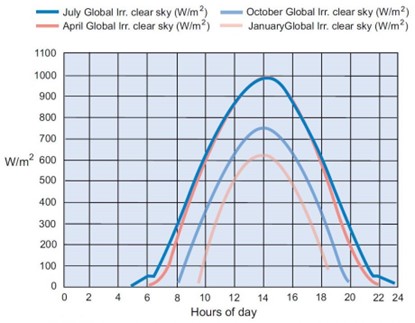One of the greater challenges faced in the production and consumption of renewable energy is in the storage of energy produced by intermittent sources. For example, wind power requires air movement that is always quite variable in duration and in strength. Locations do exist where wind speed is quite consistent, and the heights at which they are strongest can be predicted, but even the best of these sources are variable. Solar power is more predictable, with factors such as the time of year and day, temperature, angle, and type of solar collector, but it is subject to intermittent cloud cover and weather disruption. The Cambridge University Solar Installation built in 2011 has been researching the production of solar energy. The chart on the previous page shows a theoretical illustration of the possible solar production. In reality, daily production is more intermittent, which can be seen in the following two charts, the first of the production of solar energy from two days in August 2012 and the second chart showing the production over one day in July 2012.

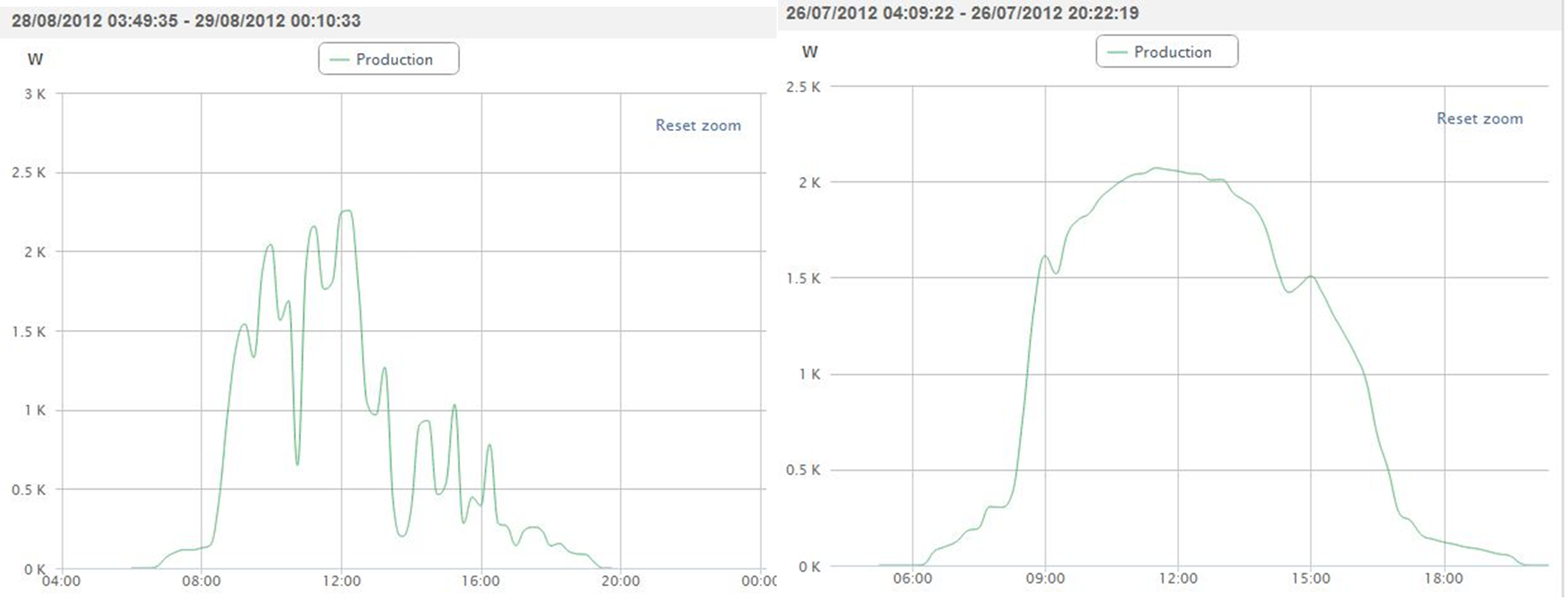
Demand for electricity is quite predictable, and renewable energy sources will either overproduce or under-produce for the needs of the region. Using Cambridge’s data^[4] one can see where a surplus of produced solar energy was exported to the main electrical grid, and when electricity had to be imported from other sources to meet the regional demand.

While these introductory physics problems look at the storage of electricity in batteries, higher level physics and engineering problems will be looking at how to efficiently store the surplus production mainly during the day to be used later when needed:

• [latex]P=\dfrac{\text{work}}{t}=\dfrac{\Delta E}{t}[/latex]
• [latex]P=IV=I^2R=\dfrac{V^2}{R}[/latex]

The common Canadian fridge from a hundred years and earlier was an ice house. A small building was insulated with sawdust with extra sawdust (acting as further insulation) between the walls and blocks of ice generally cut from a lake.

Exercise Answers

22.1 Current & Ohm’s Law

1.  6.25 × 10¹⁸ e⁻
2. 2.0 × 10¹⁰ A
3. 0.04 A
4. 0.576 C
5. 3.12 × 10¹² e⁻
6. 4.8 Ω
7. 0.20 A
8. 24 Ω
9. 250 V
10. Draws 10A – would trip the circuit
    1. 20 A – Microwave trips the circuit
    2. 5 A over

22.2 Electric Power

1. 19.2 Ω
2. 960 W
3. 0.83 A
4. 8.33 A. It will not trip the breaker
5. 83.3 A
6. 8.8 W
7. 3.9 × 10¹⁸ e⁻
   1. 576 Ω
   2. 0.21 A
   3. 25 W

22.3 Electrical Energy of Batteries

1. 8.64 × 10⁵ W
2. 9600 W or 9.6 kW
3. 6250 s or 1.74 h
4. 94 h
5. 540 A
   1. 8.4 W
   2. 1.5 × 10⁴ J

22.4 Electric Power & Energy

1. 1. $1000
   2. 4.3 years
   3. $15.6 Billion
   4. varies
2. 1. Cold = 108 kWh    Hot = 2180 kWh
   2. Cold = $11.90  Hot = $239.80
3. 1.1 × 10⁶ J/kg
4. 1. 1.38 GJ
   2. 384 kWh
   3. $42.24

Media Attributions

• “Alessandro Volta’s electric battery (Tempio Voltiano, Como, Italy)” by GuidoB is licensed under a CC BY-SA 3.0 licence.