15 Energy & Heat

Resources

Equations Introduced and Used for this Topic:

  • [latex]Q = mc\Delta T[/latex]
  • [latex]Q =\pm mL_f[/latex]
  • [latex]Q =\pm mL_v[/latex]

Where…

  • [latex]Q[/latex] is the heat (energy), measured in joules (J)
  • [latex]L_v[/latex] is the latent heat of vaporization, measured in joules/kilograms (J/kg)
  • [latex]L_f[/latex] is the latent heat of fusion, measured in joules/kilograms (J/kg)
  • [latex]∆T[/latex] is the change in temperature, measured in Celsius (°C) or Kelvin (K)
  • [latex]c[/latex] is the specific heat constant, measured in joules/kilograms degrees Celsius (J/kg°C). Specific heat is found by experiment but has a rough value for specific temperature ranges.
  • [latex]m[/latex] is the mass of the object or substance being heated/cooled, measured in kilograms (kg)
Specific Heat
Material Specific Heat Material Specific Heat
Aluminum 900 J/kg°C Lead 160 J/kg°C
Brass 384 J/kg°C Mercury 139 J/kg°C
Copper 390 J/kg°C Pyrex 837 J/kg°C
Ethanol 2400 J/kg°C Silver 235 J/kg°C
Glass 840 J/kg°C Steel 445 J/kg°C
Ice 2100 J/kg°C Steam 2020 J/kg°C
Iron 460 J/kg°C Water 4187 J/kg°C
Latent Heats of Fusion and Vaporization
Material Lf (J/kg) Lv (J/kg)
Water 3.34 × 105 2.26 × 106
Mercury 1.18 × 104 2.96 × 105
Ethyl Alcohol 1.05 × 105 8.54× 105
Nitrogen 2.55 × 104 1.99 × 105
Oxygen 1.38 × 104 2.13 × 105
Hydrogen 5.86 × 104 4.52 × 105
Helium 5.23 × 103 2 × 104
Fusion and Vaporization Temperatures
Material Tf (°C) Tv (°C)
Water 0 100
Mercury −38.8 356.7
Aluminum 660.3 2519
Nitrogen −210 −195.8
Oxygen −218.8 −183
Hydrogen −259.1 −252.9
Helium −272.2 −268.9

15.1 Specific Heat Capacity

Equations Introduced or Used for this Section:

[latex]Q = mc\Delta T[/latex]

Specific Heat
Material Specific Heat Material Specific Heat
Aluminum 900 J/kg°C Lead 160 J/kg°C
Brass 384 J/kg°C Mercury 139 J/kg°C
Copper 390 J/kg°C Pyrex 837 J/kg°C
Ethanol 2400 J/kg°C Silver 235 J/kg°C
Glass 840 J/kg°C Steel 445 J/kg°C
Ice 2100 J/kg°C Steam 2020 J/kg°C
Iron 460 J/kg°C Water 4187 J/kg°C

Heat and Temperature

Specific Heat Capacity (Q) – or heat capacity – refers to the ability of a system or body’s capability of absorbing or losing energy (heat energy) without changing its original state of solid, liquid, gas or plasma. What does occur in this setting is that the temperature of the object or system will change according to its gaining or losing heat energy.

Temperature (T) refers to a measured value of a body using a thermometer that is calibrated in one or more scales such as Celsius (°C) or Kelvin (K) and in some cases Fahrenheit (°F). A common interpretation of temperature using the classical thermodynamics description is that it is measuring the average motion or the internal kinetic energies of the atoms or molecules making up a body or system. Temperature can also be thought of as the measurement of oscillation or vibrational motion that occurs in solids and liquids.

Early thermometers relied on the expansion of air or water as a way to measure the temperature of a body or a system. Examples of these thermometers can be seen at the Museo Galileo where the larger bulb at the bottom contains water to expand or contract and the thin tube shows this expansion using white dots representing 10 degree increments and single black dots showing single degree increments.

The beginning of precision temperature measurements is credited to Daniel Gabriel Fahrenheit (1686-1736) who based his scale on the lowest consistent temperature he could achieve in a lab by using a slurry of ice, water and salt (0°F), water and ice (32 °F) and the temperature of a human mouth or armpit (96°F). Fahrenheit deviated from the work of previous thermometer makers by using mercury as his choice of liquid to measure its expansion using heat energy.

The Celsius scale (centigrade scale) is the standard scale used in SI measurements. It is a variation of the original scale developed by Anders Celsius (1701-1744) who set the scale of 0°C as the boiling point of water and 100°C as the freezing point of water. Celsius’s scale was reversed the next year to designating 0°C to represent the freezing point and 100°C to represent the boiling point. In 1954, the lowest possible temperature (Absolute Zero[1]) was defined to be exactly −273.15°C.

The exact equivalent measure of temperature to Celsius is the measure of Kelvin (K) which starts at Absolute Zero as 0 K. Using this scale, the melting point of water is roughly 273.15 K and the boiling point is 373.15 K. Human temperature works out to be an average of 310.15 K.

For conversions:

Kelvin = Celsius + 273.15° and Fahrenheit = [latex]\dfrac{5}{9}[/latex] (Celsius − 32°)

The Conceptual Development of Heat

Some of the earliest conceptions of heat are from 3000 B.C., and can be found recorded in Egyptian hieroglyphs that relate heat to fire. While only fragments of the writings of Heraclitus (535 BCE-475 BCE) exist, recorded as quotes from other authors, his concept of heat (fire) was that it was responsible for controlling the nature of the other principle elements of earth and water. Al-Biruni (973-1050) related heat to the concept of movement and friction, where heat or cold related to motion of lack of motion by air. This concept of heat as related to motion was echoed and refined by a number of philosophers that followed: Abu Ali Sina (980-1037), Francis Bacon (1561-1626) and Robert Hooke (1635-1703).

Article to Read: The logic of Phlogiston

Dominant in the historical development of the concept of heat was the phlogiston theory, which was later replaced by caloric theory. Phlogiston was considered to be an undetectable fluid-like substance that filled the spaces between matter. The properties of phlogiston, as needed to explain chemical and physical phenomenon, were in the end what scientists used to dismiss the fluid theory of heat.

The defining phenomenon used to dismiss phlogiston theory came from Sir Benjamin Thompson, a.k.a. Count Rumford[2] (1753-1814), who found that it was the byproduct of mechanical energy from friction that produced heat and not some mysterious fluid that was being leaked from the substance. His breakthrough demonstration in 1804 was to immerse a cannon into a barrel of water and then use a dull drill bit to try to bore out the cannon. What happened is that the cold water in the barrel[3] was brought to a boil within  2 1/2 hours, and no metal was removed from the barrel of the cannon, which meant that no phlogiston fluid from the cannon was escaping. Instead the amount of heat that was created was directly related to the amount of friction that was being produced.

Within a few decades, quantification experiments by James Joule (1818-1889), Robert Mayer (1814-1878) and others established a clear and measurable relationship between heat, mechanical energy and work. In 1847 Hermann Helmholtz (1821-1894) generalized the relationship between heat, mechanical energy and work into a universal law governing the conservation of energy. This came to be known as the First Law of Thermodynamics.

The First Law of Thermodynamics is a variation of the Law of Conservation of Energy that was adapted for Thermodynamic Systems[4].  It can be stated as follows: The total energy of an isolated system is constant where energy can be transformed from one form to another but energy can be neither created nor destroyed.  In an equation this is written as:

Internal Energy of a System = Heat added to a System − Work done by the System

or … [latex]\Delta U=Q−W[/latex]

The year 1850 was a watershed in the history of science, marking the unification of the various and quite different studies of motion, light, heat, electricity, and magnetism under the umbrella of energy.  Energy became the unifying concept that linked all of the above disparate fields of studies together and, as some historians argue, replaced the dominance of Astronomical studies with Physics.

Heat is generally taught today as energy transferred between two systems or bodies due to a temperature difference or as a by-product of friction.

Specific Heat Capacity

Specific heat is the measure of the amount of heat energy needed to raise the temperature of a mass of one kilogram (kg) or gram (g) by one degree centigrade (1 °C) .  This relationship allows one to quantify the amount of heat specific to substances.

This relationship is quantified as:

[latex]Q = mc\Delta T[/latex]

The constant “c” used in this equation is only an average constant for the substance, and generally falls as the temperature of the body decreases. Water is an unusual substance that has one of the highest heat capacity values of all substances. As such, it is incredibly important to moderating and maintaining stable climate environments on the planet and moderating the internal temperature of living organisms. All specific heats vary with temperature and composition.

Example 15.1.1

1.5 kg of Pyrex glass (specific heat 837 J/kg°C) loses 2.51 × 104 J of heat.  If the temperature of the glass is 80°C before cooling what is its final temperature?

Solution

Data:

  • [latex]Q[/latex] = 2.51 × 104 J
  • [latex]m[/latex] = 1.5 kg
  • [latex]c_{\text{pyrex}}[/latex] = 837 J/kg°C
  • [latex]T_i[/latex] = 80°C
  • [latex]T_f[/latex] = Find

Solution:

  • [latex]Q = mc\Delta T[/latex]
  • [latex]-2.51\times10^4\text{ J}=(1.5\text{ kg})(837\text{ J/kg°C})(T_f-80\text{°C})[/latex]
  • [latex]T_f-80\text{°C}=-2.51\times10^4\text{ J}\div 1256\text{ J/°C}[/latex]
  • [latex]T_f=60\text{°C}[/latex]

Example 15.1.2

Calculate the specific heat of a 286 kg piece of steel if 2.54 × 107 J of heat is required to raise its temperature from 20°C to 220°C.

Solution

Data:

  • [latex]Q[/latex] = 2.54 × 107 J
  • [latex]m[/latex] = 286 kg
  • [latex]T_i[/latex] = 20°C
  • [latex]T_f[/latex] = 220°C
  • [latex]c_{\text{steel}}[/latex] = Find

Solution:

  • [latex]Q = mc\Delta T[/latex]
  • [latex]2.54\times10^7\text{ J}=(286\text{ kg})(c_{\text{steel}})(220\text{°C}-20\text{°C})[/latex]
  • [latex]2.54\times10^7\text{ J}=(c_{\text{steel}})(57200\text{ kg°C})[/latex]
  • [latex]c_{\text{steel}}=2.54\times10^7\text{ J}\div 572000\text{ kg°C}[/latex]
  • [latex]c_{\text{steel}}=444\text{ J/kg°C}(\approx440\text{ J/kg°C})[/latex]

Example 15.1.3

By how much should the temperature of a 500 g mass of lead change if 6560 J of heat is added to it?  (Specific heat of lead is 129 J/kg°C).

Solution

Data:

  • [latex]Q[/latex] = 6560 J
  • [latex]m[/latex] = 0.500 kg
  • [latex]c_{\text{lead}}[/latex] = 129 J/kg°C

Solution:

  • [latex]Q = mc\Delta T[/latex]
  • [latex]6560\text{ J}=(0.500\text{ kg})(129\text{ J/kg°C})(\Delta T)[/latex]
  • [latex]6560\text{ J}=(64.5\text{ J/kg°C})(\Delta T)[/latex]
  • [latex]\Delta T=6560\text{ J}\div 64.5\text{ J/kg°C}[/latex]
  • [latex]\Delta T=120\text{°C}[/latex]

Example 15.1.4

A 450 g Pyrex beaker contains 185 g of water at 21.0°C. Given that the specific heat of Pyrex is 837 J/kg°C, how much heat is needed to raise the temperature of this glass and water to 100°C?

Solution

Data:

  • [latex]Q[/latex] = Find
  • [latex]m_{\text{water}}[/latex] = 0.185 kg
  • [latex]m_{\text{pyrex}}[/latex] = 0.450 kg
  • [latex]T_i[/latex] = 21.0°C
  • [latex]T_f[/latex] = 100°C
  • [latex]c_{\text{pyrex}}[/latex] = 837 J/kg°C
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C

Solution:

  • [latex]Q = mc\Delta T+mc\Delta T[/latex] (water + pyrex)
  • [latex]Q=(0.450\text{ kg})(837\text{ J/kg°C})(100\text{°C}-21.0\text{°C})+(0.185\text{ kg})(4187\text{ J/kg°C})(100\text{°C}-21.0\text{°C})[/latex]
  • [latex]Q=29760\text{ J}+61200\text{ J}[/latex]
  • [latex]Q=90960\text{ J}(\approx91000\text{ J}[/latex]

Exercise 15.1

  1. How much heat is required to raise the temperature of 153 kg of water from 15.0 °C to 35.0 °C?
  2. How much heat is lost if 865 g of aluminum (specific heat 900 J/kg°C) is cooled from 120 °C to 55 °C ?
  3. 585 kg of Pyrex glass (specific heat 837 J/kg°C) loses 8.65 × 106 J of heat. If the temperature of the glass is 95.8 °C before cooling what is its final temperature?
  4. Calculate the specific heat of a 286 kg piece of steel if 5.53 × 107 J of heat is required to raise its temperature from 22 °C to 452 °C.
  5. By how much should the temperature of a 2.75 kg mass of lead change if 2.84 × 104 J of heat is added to it? (Specific heat of lead is 129 J/kg°C).
  6. What is the maximum mass of water that can be brought from 15.0 °C to its boiling point if 2.93 × 106 J of heat is available?
  7. Calculate the specific heat of a 300 kg piece of a steel alloy, if 5.93 × 107 J is required to raise its temperature from 25 °C to 450° C.
  8. A 215 g glass beaker contains 145 g of water at 18.5 °C. If the specific heat of glass is 840 J/kg°C,  how much heat is needed to raise the temperature of this glass and water to 98.5 °C?

15.2 Heat & Phase Changes

Equations Introduced or Used for this Section:

  • [latex]Q =\pm mL_f[/latex]
  • [latex]Q =\pm mL_v[/latex]

Where…

  • [latex]Q[/latex] is the heat (energy), measured in joules (J)
  • [latex]L_v[/latex] is the latent heat of vaporization, measured in joules/kilogram (J/kg)
  • [latex]L_f[/latex] is the latent heat of fusion, measured in joules/kilogram (J/kg)
  • [latex]m[/latex] is the mass of the object being heated or cooled, measured in kilograms (kg)
Latent Heats of Fusion and Vaporization
Material Lf (J/kg) Lv (J/kg)
Water 3.34 × 105 2.26 × 106
Mercury 1.18 × 104 2.96 × 105
Ethyl Alcohol 1.05 × 105 8.54× 105
Nitrogen 2.55 × 104 1.99 × 105
Oxygen 1.38 × 104 2.13 × 105
Hydrogen 5.86 × 104 4.52 × 105
Helium 5.23 × 103 2 × 104
Fusion and Vaporization Temperatures
Material Tf (°C) Tv (°C)
Water 0 100
Mercury −38.8 356.7
Aluminum 660.3 2519
Nitrogen −210 −195.8
Oxygen −218.8 −183
Hydrogen −259.1 −252.9
Helium −272.2 −268.9

Phase changes are used to describe the change in state that occurs in a substance as it changes from a solid to a liquid to a gaseous state or sometimes to plasma. A feature of phase change is that bodies can change state without changing temperature. The earliest record of this observation dates back to 1761 when Joseph Black (1728-1799)[5] announced his discovery that ice absorbs heat without changing temperature in the process of melting. Black went on to show that different substances have different specific heats.

While the enthalpy of systems defines four changes of state, only the phase change between solids & liquids and liquids & gases will be analyzed.

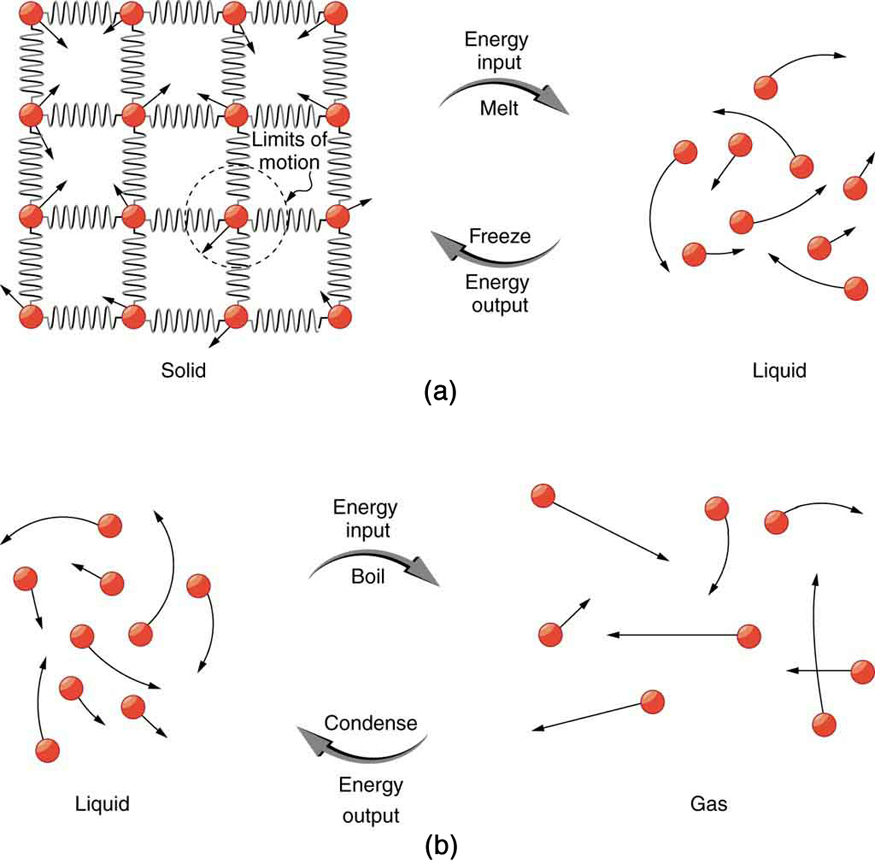
At the atomic level, what is visualized is in the transition between solid, liquid and gaseous states. In the sketch to the left the transition from (a) solid to liquid and the reverse is described as either freezing or melting. The equation used to quantify this transition is: [latex]Q =\pm mL_f[/latex] where the + or − sign refers to either the system absorbing energy to melt or losing energy to freeze.

For the transition from liquid to a gaseous state (b) the changes of states are described as vaporization or condensation. The equation quantifying this transition is: [latex]Q =\pm mL_v[/latex] where the + or − sign refers to either the system absorbing energy to vaporize or losing energy to condense. Neither equation makes any reference to temperature; if the positive sign is used, the system is absorbing energy and if the negative sign is used the system is losing energy.

The following examples work with the change in state of some substance.

Example 15.2.1

On the following phase change diagram of water changing from ice to steam show the following: temperature for the phase changes, the positive/negative signs for the phase changes that indicate the system is gaining or losing energy with the corresponding names of these changes.

Example 15.2.2

How much heat is required to melt 100 kg of ice at 0 °C?

Solution

Data:

  • [latex]Q[/latex] = find
  • [latex]m[/latex] = 100 kg
  • [latex]L_f[/latex] = 3.34 × 105 J/kg

Solution:

  • [latex]Q=+mL_f[/latex]
  • [latex]Q[/latex] = − (12 kg)(2.26 × 106 J/kg)
  • [latex]Q[/latex] = − 2.71 × 107 J (≈ − 2.7 × 107 J)

Example 15.2.3

How much heat is released when 12 kg of steam at 100 °C is condensed to water at the same temperature?

Solution

Data:

  • [latex]Q[/latex] = find
  • [latex]m[/latex] = 12 kg
  • [latex]L_v[/latex] = 2.26 × 106 J/kg

Solution:

  • [latex]Q = -mL_v[/latex]
  • [latex]Q[/latex] = − (12 kg)(2.26 × 106 J/kg)
  • [latex]Q[/latex] = −2.71 × 107 J (≈ −2.7 × 107 J)

Example 15.2.4

How much heat is required to convert 250 g of ice at −10.0 °C to steam at 100 °C?

Solution

Data:

  • [latex]Q[/latex] = Find
  • [latex]m[/latex] = 0.25 kg
  • [latex]L_v[/latex] = 2.26 × 106 J/kg
  • [latex]L_f[/latex] = 3.34 × 105 J/kg
  • [latex]c_{\text{ice}}[/latex] = 2100 J/kg°C
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C

Solution:

  • [latex]Q=mc\Delta T+mL_f+mc\Delta T+mL_v[/latex]
  • [latex]Q[/latex] = (0.250 kg)(2100 J/kg°C)(0°C − −10°C) + (0.250 kg)(3.34 × 105 J/kg) + (0.250 kg)(4187 J/kg°C)(100°C − 0°C) + (0.250 kg)(2.26 × 106 J/kg)
  • [latex]Q[/latex] = 5250 J + 83500 J + 104000 J + 565000 J
  • [latex]Q[/latex] = 758000 J

Example 15.2.5

How much heat must be extracted to change 454 g of water at 20°C into ice at −6°C?

Solution

Data:

  • [latex]Q[/latex] = Find
  • [latex]m[/latex] = 0.454 kg
  • [latex]L_f[/latex] = 3.34 × 105 J/kg
  • [latex]c_{\text{ice}}[/latex] = 2100 J/kg°C
  • [latex]c_{\text{water}}[/latex] = 4187 J/kg°C

Solution:

  • [latex]Q=mc\Delta T-mL_f+mc\Delta T[/latex]
  • [latex]Q[/latex] = (0.454 kg)(2100 J/kg°C)(−6°C − 0°C) − (0.454 kg)(3.34 × 105 J/kg) + (0.454 kg)(4187 J/kg°C)(0°C − 20°C)
  • [latex]Q[/latex] = −5720 J − 151600 J − 38000 J
  • [latex]Q[/latex] = −195000 J (≈ −200000 J)

Exercise 15.2

  1. How much heat is required to melt 28.6 kg of ice at 0°C?
  2. How much heat is released when 423 g of steam at 100 °C is condensed to water at the same temperature?
  3. If 1.85 × 104 J of heat is released when 3.85 × 10−3 kg of tungsten is condensed at its boiling point what is the latent heat of vaporization of tungsten?
  4. What mass of ethanol can be solidified by the removal of 9.53 × 104 J of heat at its melting point? The latent heat of fusion of ethanol is 1.05 × 105 J/kg.
  5. How much heat is released when 454 g of steam at 100°C is condensed into water at the same temperature?
  6. A cooler is able to condense 12.0 kg of steam at 100°C into water at 100°C? in 2.0 h. Using this same cooler, what mass of water at 0°C should it be able to freeze into ice at 0°C in 2.0h?
  7. How much heat must be extracted from a litre of water at 50°C to turn it into ice at 0°C?
  8. How much heat is required to convert 1.15 kg of ice 0.00 °C to water at 21.5 °C ?
  9. How much heat is required to convert 86.3 g of ice at −5.0 °C to steam at 100 °C?
  10. How much heat must be extracted to change 500 g of water at 5.0°C into ice at −8.0°C?
  11. How much heat is required to change 4.0 kg of ice at 0°C to steam at 100°C?
  12. How much heat is need to melt the 2.5 × 1019 kg of ice in Antarctica if we assume an ice temperature of −45 °C? How does this compare to all the energy of the Sun striking the Earth in one year?  (Total solar energy incident on Earth is 5.4 × 1024 J each year.)
  13. If the entire 2 850 000 km3 of Greenland[6] ice sheet were to melt global sea levels would rise 7.2 m. If we are to assume that the average temperature of this ice is −25 °C, how much energy is needed to turn Greenland’s ice cap into water at 0 °C?

Exercise 15.3.1: Heating Canada’s Homes – An Exercise in the Geography of Energy

A typical sized family home consumes about 1500 m3 of natural gas a year to heat (19°C). This is equivalent to about 57 GJ of energy.

  1. If we were to use wood with an energy density of 1.5 × 107 J/kg, how many kg would we need to heat this house?
  2. If a hectare of forest provides 100000 kg of wood, how much wood would be needed to heat all of Canada’s 12 million or so homes?
  3. If we consider that a tree takes roughly 100 years to reach an optimal size for harvesting, what size of forest in Canada would we need to have sustainable heating?
  4. How does the sustainable forest needed for heating compare to Canada’s forest and wooded areas of roughly 400 million hectares?
  5. How does this compare to BC’s forest and wooded areas of 64 million hectares?

Exercise 15.3.2: Yearly Melt of Arctic Sea Ice

  1. If we assume an average thickness of 2.5 m for this ice being melted and that the ice is at a temperature of −50°C, how much energy is absorbed by this process in a year?

Arctic melts around 8 000 000 km2 (2.5 m thick) Heat needed = ______________

Exercise Answers

15.1 Specific Heat Capacity

  1. 1.28 × 107 J
  2. − 50600 J
  3. 78.1 °C
  4. 450 J/kg°C
  5. 79.4 °C
  6. 8.25 kg
  7. 465 J/kg°C
  8. 6.3 × 104 J

15.2 Heat & Phase Changes

  1. 9.55 × 106 J
  2. 9.56 × 105 J
  3. 4.81 × 106 J/kg
  4. 0.908 kg
  5. 1.03 × 106 J
  6. 81.2 kg
  7. − 5.43 × 105 J
  8. 4.87 × 105 J
  9. 2.61 × 105 J
  10. − 1.85 × 105 J
  11. 1.21 × 107 J
  12. 1.07 × 1025 J

15.3.1 Heating Canada’s Homes

  1. 3800 kg
  2. 456000 ha/y
  3. 45.6 million hectares
  4. [latex]\dfrac{57}{500}[/latex] or 11.4%
  5. [latex]\dfrac{57}{80}[/latex] or 71%

15.3.2 Yearly Melt of Arctic Sea Ice

  1. 8 × 1021 J

Media Attributions

  1. In Fahrenheit, Absolute Zero is defined as −459.67°F ↵
  2. Benjamin Thompson (Count Rumford) has been quite entertaining for historians to research due to his military, political and amorous adventures. ↵
  3. Count Rumford recorded the amount of water in the barrel to be 2 1⁄4 wine gallons. ↵
  4. Reference - Thermodynamic System: https://en.wikipedia.org/wiki/Thermodynamic_system ↵
  5. Black’s discoveries arose from his work for producers of Scotch whisky in search of the ideal quantity of fuel and water for distillation purposes. ↵
  6. The mass of the Greenland ice sheet is approximately 2.62 × 1015 kg. ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Foundations of Physics Copyright © by Terrance Berg is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book