1 Measurement and Solutions

1.1 Metric to English (US) Conversions

Resources

Distance

  • 12 in = 1 ft
  • 3 ft = 1 yd
  • 1760yd = 1 mi
  • 5280 ft = 1 mi
  • 1 inch = 2.54 cm
  •  1 ft = 0.3048 m
  • 1 mile = 1.602 km
  • 1 Nautical Mile = 1852 m
  • 10 mm = 1 cm
  • 1000 mm = 1 m
  • 100 cm = 1 m
  • 1000 m = 1 km

Area

  • 144 in2 = 1 ft2
  • 1 in2 = 6.45 cm2
  • 10000 cm2 = 1 m2
  • 43560 ft2 = 1 acre
  • 1 ft2 = 0.092903 m2   
  • 10000 m2 = 1 hectare
  • 640 acres = 1 mi2
  • 1 mi2 = 2.59 km2
  • 100 hectare = 1 km2

Volume

  • 57.75 in3 = 1 qt
  • 16.39 cm3 = 1 in3
  • 1 cm3 = 1 ml
  • 4 qt = 1 gal
  • 1 ft3 = 0.0283168 m3
  • 1000 ml = 1 liter
  • 42 gal (oil) = 1 barrel
  • 3.79 liters = 1 gal
  • 1000 liter = 1 m3  

Mass/Weight

  • 437.5 grains = 1 oz
  • 453 g = 1 lb.
  • 1000 mg = 1 g
  • 16 oz = 1 lb.
  • 2.2 lb. = 1 kg
  • 1000 g = 1 kg
  • 2000 lb. = 1 short ton
  • 1000 kg = 1 metric ton

Time

  • 1 h = 60 min
  • 1 min = 60 s
  • 1 yr = 365.2425 day (average)
  • 1 h = 3600 s
  • 1 day = 24 h
  • 1 yr = 365.25 day (Astronomical)

Temperature

Fahrenheit to Celsius conversion table.

Fahrenheit to Celsius Conversions:  °C = [latex]\frac{5}{9} (°F - 32)[/latex] and [latex]°F = \frac{9}{5} (°C + 32)[/latex]

Dimensional Analysis

As a student of physics, one of the challenges you encounter in physics deals with converting units. In converting units of measure, you can multiply several fractions together in a process known as dimensional analysis. In dimensional analysis, you create a fraction that equals one, so when it is multiplied to another fraction, it does not change the actual measure; instead, it changes to some equivalent measure.

The challenge in doing this is to decide which fractions to multiply correctly. One process in doing this is to decide which unit of measure you wish to replace and to substitute the equivalent measure in the form you desire. This is done so that the undesired unit is cancelled out when multiplied by this equivalent fraction, which leaves the desired unit to take its place.

You can see this process used in the following examples.

Example 1.1

If 1 pound (lb) = 16 ounces (oz), how many pounds are in 435 ounces?

Solution

[latex]435\text{ oz}=435\text{ oz}\times\dfrac{1\text{ lb}}{16\text{ oz}}[/latex] This operation cancels the oz and leaves the units of the lb.
[latex]435\text{ oz}=\dfrac{435\text{ lb}}{16}[/latex] Which then reduces to
[latex]435\text{ oz}=27\frac{3}{16}\text{ lb}[/latex]

The same process can be used to convert problems with several units in them.  Consider the following example.

Example 1.2

A student averaged 45 miles/hour (mi/h) on a trip. What was the student’s speed in feet/second (ft/s)?

Solution

[latex]\dfrac{45 \text{ mi}}{\text{hr}} = 45 \text{ mi} \times \dfrac{5280 \text{ ft}}{1 \text{ mi}} \times \dfrac{1 \text{ hr}}{3600 \text{ s}}[/latex] This will cancel the units of mi & hr, and leave ft & s
[latex]\dfrac{45 \text{ mi}}{\text{hr}} = 45 \times \dfrac{5280}{} \times \dfrac{1}{1} \dfrac{\text{ft}}{3600 \text{ s}}[/latex] This then reduces to
[latex]45 \text{ mi/hr} = 66 \text{ ft/s}[/latex]

Example 1.3

Convert 8 cubic feet (ft3) to cubic yards (yd3).

Solution

[latex]8 \text{ ft}^{3} = 8 \text{ ft}^{3} \times \dfrac{(1 \text{ yd})^{3}}{(3 \text{ ft})^{3}}[/latex] This will cancel the units ft3 and replace them with yd3
[latex]8 \text{ ft}^{3} = 8 \text{ ft}^{3} \times \dfrac{1 \text{ yd}^{3}}{27 \text{ ft}^{3}}.[/latex] Cube the parenthesis
[latex]8 \text{ ft}^3 = 8 \times \dfrac{1 \text{ yd}^3}{27}[/latex] Which then reduces to
[latex]8 \text{ ft}^3 = \dfrac{8}{27} \text{ yd}^{3}[/latex], (≈ 0.3 yd3)

Example 1.4

A room is 10 ft by 12 ft.  How many square yards are in the room? The area of the room is 120 square feet (ft2). ([latex]Area = Length \times Width[/latex]).

Solution

[latex]120 \text{ ft}^2 = 120 \text{ ft}^2 \times \dfrac{(1 \text{ yd})^3}{(3 \text{ ft})^2}[/latex] Convert the area. Cancel ft2 and replace with yd2
[latex]120 \text{ft}^2 = \dfrac{120 \text{yd}^2}{9}[/latex] This then reduces to
[latex]120 \text{ft}^2 = 13 \dfrac{1}{3} \text{ yd}^2[/latex]

The process of dimensional analysis can be used to convert other types of units as well.  If we can identify relationships that represent the same value we can make them into a conversion factor.

Example 1.5

A child is prescribed a dosage of 12 mg of a certain drug per day and is allowed to refill his prescription twice.  If there are 60 tablets in a prescription, and each tablet has 4 mg, how many doses are in the 3 prescriptions (original + 2 refills)?

Solution

[latex]\begin{array}{l}3 \text{ Prescriptions} = \\ 3 \text{ Prescriptions} \times \dfrac{60 \text{ tablets}}{1 \text{ prescription}}\times \dfrac{4 \text{ mg}}{1 \text{ tablet}}\times \dfrac{1 \text{ dosage}}{12\text{ mg}}\end{array}[/latex] This cancels all unwanted units
[latex]3 \text{ Prescriptions} = \dfrac{3 \times 60 \times 4 \times 1}{1 \times 1 \times 12} \text{ or } \dfrac{720}{12} \text{ dosages}[/latex] Which then reduces to
[latex]3 \text{ Prescriptions} = 60 \text{ daily dosages}[/latex]

Exercise 1.1

Write the corresponding names behind the given unit.

One Dimensional Measures:

  • mi                              
  • oz                              
  • mg                              
  • km                              
  • mm                              
  • ft                              
  • yd                              
  • t                              
  • g                              
  • cm                              
  • μm                              
  • in                              

Two Dimensional Measures:

  • ft2                              
  • m2                              
  • km2                              
  • in2                              
  • yd2                              
  • cm2                              
  • mm2                              
  • μm2                              

Three Dimensional Measures:

  • ft3                              
  • m3                              
  • km3                              
  • in3                              
  • yd3                              
  • cm3                              
  • mm3                              
  • μm3                              

 

Exercise 1.2

Convert the following measures.

  1. 7 miles (mi) to yards (yd)
  2. 234 ounces (oz) to short tons (t)
  3. 11.2 milligrams (mg) to grams (g)
  4. 1.35 kilometres (km) to centimetres (cm)
  5. 9800000 millimetres (mm) to miles (mi)
  6. 4.5 square feet (ft2) to square yards (yd2)
  7. 435000 square metres (m2) to square kilometres (km2)
  8. 8.0 square kilometres (km2) to square feet (ft2)
  9. 0.0065 cubic kilometres (km3) to cubic metres (m3)
  10. 14.62 square inches (in2) to square centimetres (cm2)
  11. 5500 cubic centimetres (cm3) to cubic yards (yd3)
  12. 3.5 miles per hour (mi/h or mph) to feet/second (ft/s)
  13. 185 yards per minute (yd/min) to miles per hour (mi/h or mph)
  14. 153 feet per second (ft/s) to miles per hour (mi/h or mph)
  15. 248 miles per hour (mi/h or mph) to metres/second (m/s)
  16. 186000 miles per hour (mi/h or mph) to kilometres per year (km/a or km/yr)
  17. 7.50 tons per square yards (t/yd2) to tons per square inches (t/in2)
  18. 16 feet per second squared (ft/s2) to kilometres per hour squared (km/h2)

Exercise 1.3: Measures of Length and Weight, Time Zones

  1. How many palms are in one league?
  2. How many points are equal to a poppyseed?
  3. Convert your weight in stones. For this you need to research the internet to find which stone conversion to use.
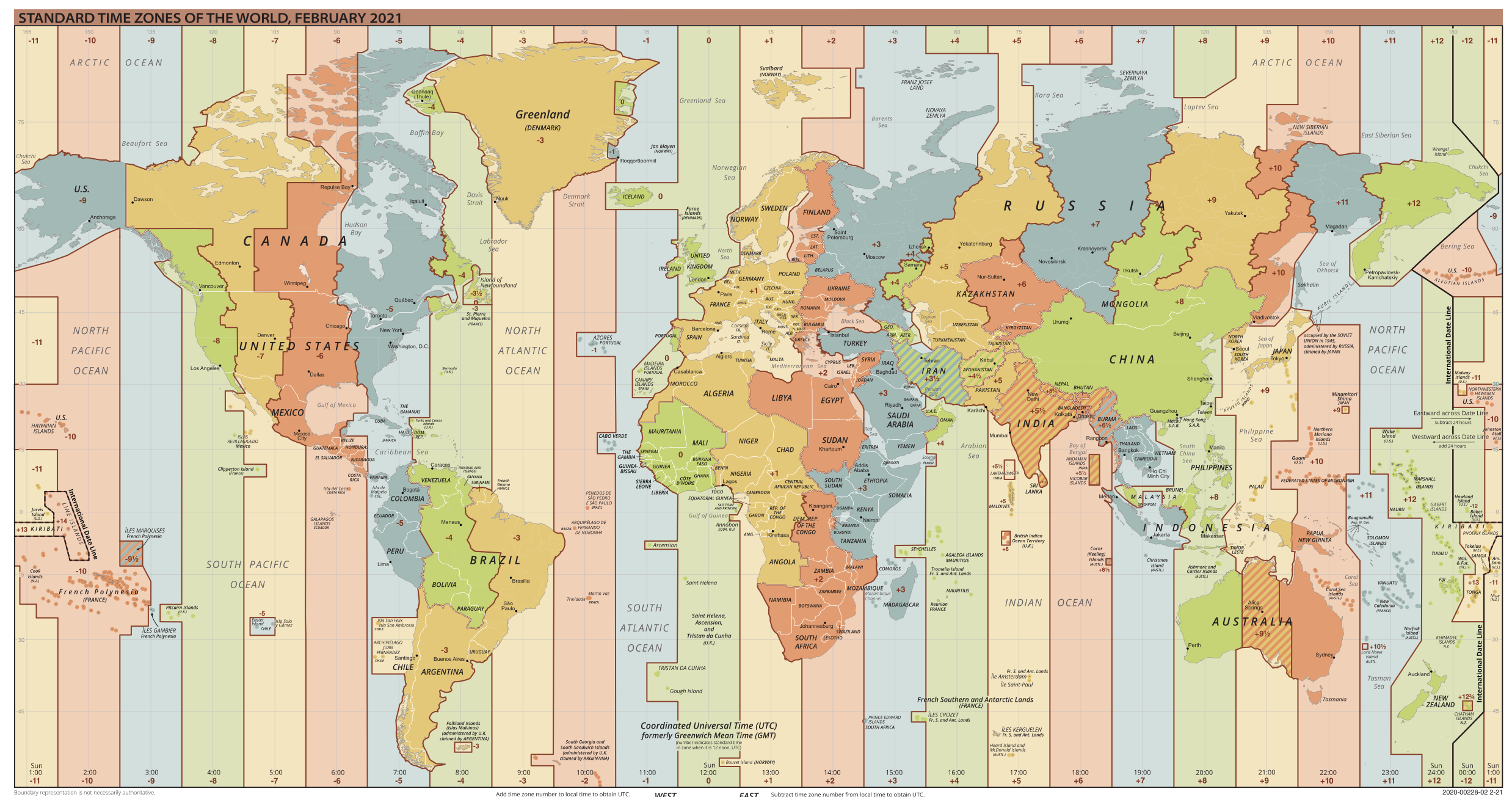
  4. Using the Standard Time Zones of the World, what are the most time zones you can find for the same latitude?[1]

 

SS Warrimoo Position and Date Oddity

The passenger steamer SS Warrimoo was quietly knifing its way through the waters of the mid-Pacific on its way from Vancouver to Australia. The navigator had just finished working out a star fix and brought the master, Captain John Phillips, the result. The Warrimoo’s position was latitude 0° 31’ North and longitude 179° 30’ West. The date was 30 December 1899 and it was quickly known that they were only a few miles from the intersection of the Equator and the International Date Line.

Captain Phillips was prankish enough to take full advantage of the opportunity for achieving the navigational freak of a lifetime. He called his navigators to the bridge to check and double check the position of the ship. He changed course slightly to bear directly on his mark. Then he adjusted the engine speed. The calm weather and clear night worked in his favour. At midnight the Warrimoo lay on the Equator at exactly the point where it crossed the International Date Line!

The consequences:  The forward part of the ship was in the Southern Hemisphere, and the middle of summer and the stern was in the Northern Hemisphere and the middle of winter. The date in the aft part of the ship was December 31, 1899, while in the forward, it was January 1, 1900. This ship was, therefore, not only in two different days, two different months, two different seasons and two different years but in two different centuries, all at the same time.

Exercise 1.4: Exponential Growth

One sometimes runs into the challenge of how many times can one fold a piece of paper. The result seems to work out to a maximum of 7 or 8 times with the wad of paper growing increasingly thicker. Every fold doubles the thickness of the paper being folded. This ends up being an exponential problem where the thickness of the paper being folded can be found from the following equation:

[latex]\text{Thickness}=(\text{thickness of a single sheet of paper})\times2^{\text{number of folds}}[/latex]

or simply:

[latex]\text{Thickness}=(0.0001\text{ m})\times2^{\text{n}}[/latex]

This means…

  • For n = 1 (1 fold), the thickness is [latex](0.0001 \text{ m}) \times 21[/latex] which equals 0.0002 m.
  • For n = 2 (2 folds), the thickness is [latex](0.0001 \text{ m}) \times 22[/latex] which equals 0.0004 m.
  • For n = 3 (3 folds), the thickness is [latex](0.0001 \text{ m}) \times 23[/latex] which equals 0.0008 m.

Imagine that someone is able to fold the paper once every week for a year (52 folds). The thickness of this folded paper is surprising.

Question:

  1. How thick would a piece of paper be if it could be folded 52 times?
  2. How does this compare to the distance from the Earth to the Sun?
    ([latex]d = 1.496 \times 1011 \text{ m}[/latex])

Article to Read: If you fold a paper in half 103 times it’ll get as thick as the universe

Exercise Answers

1.1 Names & Measurement Terms:

One Dimensional Measures:

  • mi: mile
  • oz: ounce
  • mg: milligram
  • km: kilometre
  • mm: millimetre
  • ft: feet
  • yd: yard
  • t: ton
  • g: gram
  • cm: centimetre
  • μm: micrometre
  • in: inch

Two Dimensional Measures:

  • ft2: square feet
  • m2: square metre
  • km2: square metre
  • in2: square inch
  • yd2: square yard
  • cm2: square centimetre
  • mm2: square millimetre
  • μm2: square micrometre

 

Three Dimensional Measures:

  • ft3: cubic feet
  • m3: cubic metre
  • km3: cubic kilometre
  • in3: cubic inch
  • yd3: cubic yard
  • cm3: cubic centimetre
  • mm3: cubic millimetre
  • μm3: cubic micrometre

1.2 Convert the Following:

  1. 7 mi = 12320 yd
  2. 234 oz = 000731 ton
  3. 11.2 mg = 0.0112 g
  4. 1.35 km = 135000 cm
  5. 9800000 mm ≈ 6.12 mi
  6. 4.5 ft2 = 0.50 yd2
  7. 435000 m2 = 0.435 km2
  8. 8 km2 ≈ 87000000 ft2
  9. 0.0065 km3 = 6500000 m3
  10. 14.62 in2 ≈ 94.3 cm2
  11. 5500 cm3 ≈ 0.0072 yd3
  12. 3.5 mi/h ≈ 5.1 ft/s
  13. 185 yd/min ≈6.31 mi/h
  14. 153 ft/s ≈104 mi/h
  15. 248 mi/h ≈ 110 m/s
  16. 186000 mi/h ≈ 2.61 × 102 km/y
  17. 7.50 ton/yd2 ≈ 0.00579 ton/in2
  18. 16 ft/s2 ≈ 63000 km/h2

1.3 Measures of Length and Weight, Time Zones:

  1. 1 league = 63360 palms
  2. 1 poppyseed = 6 points
  3. 1 stone = 14 pounds (use this to convert your weight)
  4. 180° Longitude has 5 different time zones

1.4 Exponential Growth

  1. Thickness is 4.50 ×1011 m
  2. Approximately 3 times the distance from the Earth to the Sun

Media Attributions

  1. Online Time Zone Calculator ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Foundations of Physics Copyright © by Terrance Berg is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book