10 Work & Mechanical Energy
Resources
- Video to Watch: Mechanical Universe – Episode 14 – Potential Energy
- Extra Help: A-Level Physics Tutor
- Article to Read: Ultimate limit of human endurance found
Equations Introduced and Used in this Topic:
- Work [latex](W) = \vec{F}_{\text{net}} \cdot \vec{d}[/latex] or [latex]\vec{F}_{\text{net}} \vec{d} \cos ø[/latex]
- [latex]E_p = m g h[/latex]
- [latex]\Delta E_p = m g \Delta h[/latex]
- [latex]\Delta h = h_f - h_i[/latex]
- [latex]\Delta v = v_f - v_i[/latex]
- [latex]W = \Delta[/latex] Mechanical Energy
- [latex]E_k = \frac{1}{2} m v^2[/latex]
- [latex]\Delta E_k = \frac{1}{2} m \Delta v^2[/latex]
- [latex]V[/latex] or [latex]V_g = g h[/latex]
- [latex]w = m g[/latex]
(All equations are esolved as either scalar or vector)
Where…
- [latex]W[/latex] is Work, measured in joules (J)
- [latex]E_p[/latex] or [latex]\Delta E_p[/latex] is Gravitational Potential Energy or change in Gravitational Potential Energy, measured in joules (J)
- [latex]E_k[/latex] or [latex]\Delta E_k[/latex] is Kinetic Energy or change in Kinetic Energy, measured in joules (J)
- [latex]E[/latex] or [latex]\Delta E[/latex] is Energy or change in Energy, measured in joules (J)
- [latex]V[/latex] or [latex]V_g[/latex] is the Gravitational Potential, measured in newtons per kilogram (N/kg)
- [latex]m[/latex] is the Mass of the object, measured in kilograms (kg)
- [latex]g[/latex] or [latex]a_g[/latex] is the Gravitational Field Strength, measured in metres per second squared (m/s2)
- [latex]v[/latex] is the Speed of the object, measured in metres per second (m/s)
- [latex]v[/latex] or [latex]\Delta v[/latex] is the Speed or change in Speed of the object, measured in metres per second (m/s)
- [latex]v_f[/latex] & [latex]v_i[/latex] is the final and initial Speed of the object, measured in metres per second (m/s)
- [latex]F_{\text{net}}[/latex]is the Net Force or the Vector Sum of the Forces acting on a body or a system, measured in newtons (N)
- ø is the angle between the vectors of the Net Force and Displacement, measure in degrees (°)
- [latex]d[/latex] is the displacement through which the Net Force acts on a body or a System, measured in metres (m)
- [latex]h[/latex] or [latex]\Delta h[/latex] is the height or change in Vertical Height, measured in metres (m)
- [latex]h_f[/latex] & [latex]h_i[/latex] is the final and initial height of the object measured in metres (m)
Notes:
The Dot Product “[latex]\cdot[/latex]“ represents the cosine of the angle between two vectors. For Work it represents the angle between the direction of the Net Force and the displacement change.
The Cross Product “[latex]\times[/latex]“ represents the sine of the angle between two vectors. Equations using the cross product will be given later in your study of physics, such as the measure of Torque or the force on a charged particle moving in a magnetic field.
Work and Energy are measured in joules (J) or newton-metres (Nm)
For Example: Consider the following multiplication of these two vectors shown below
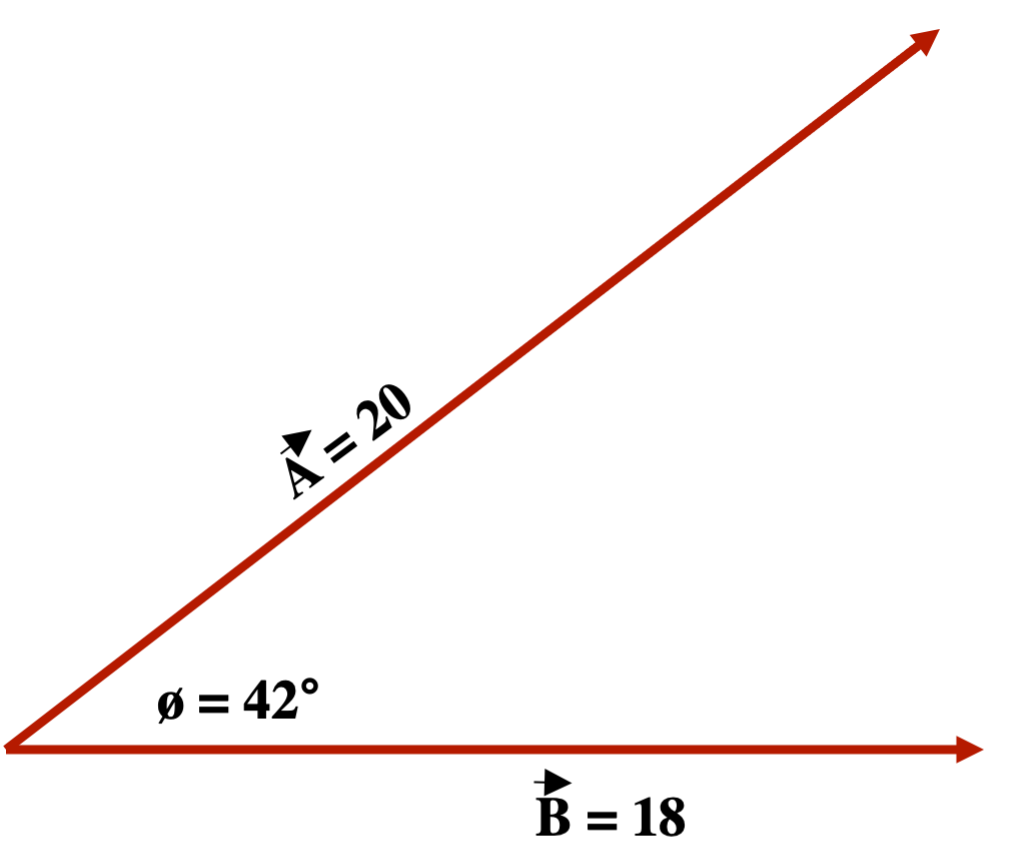
The Dot Product for these two vectors is:
- [latex]\vec{A} \cdot \vec{B} = \vec{A}\vec{B} \cos ø[/latex]
- [latex]\vec{A} \cdot \vec{B} = (20)(18) \cos 42^{\circ}[/latex]
- [latex]\vec{A} \cdot \vec{B} = 267.5[/latex] or 270
The Cross Product for these two vectors is:
- [latex]\vec{A} \times \vec{B} = \vec{A}\vec{B} \sin ø[/latex]
- [latex]\vec{A} \times \vec{B} = (20)(18) \sin 42^{\circ}[/latex]
- [latex]\vec{A} \times \vec{B} = 240.9[/latex] or 240
10.1 Kinetic and Potential Energy
- Extra Help: Potential Energy
- Extra Help: Kinetic Energy
Conceptual Development:
The concept of energy is generally credited to Aristotle’s (384 BCE-322 BCE) enérgeia (ἐνέργειά), which is a word having no direct translation into English except for “being at work”. Aristotle’s concept of work grew from Empedocles’s (490-430 BCE) thoughts on the basic elements of all matter: earth, water, air, fire and quintessence, with fire being characterized as the driver behind his thoughts and understanding leading to the concept of enérgeia. Aristotle’s concepts remained in vogue for nearly two thousand years before The Age of Enlightenment in European science began to take prominence in creating a new paradigm to understand energy.
The first of these developments was in 1669 by Christian Huygens (1629 -1695), who recognized that in a specific collision between two hardwood spheres (close to an elastic collision) the product of mass times the square of the speed[1] was conserved along with what became known as momentum. This discovery is credited as the origin of the modern concepts of mechanical energy, specifically kinetic energy. Huygens’s name for his discovery was not energy but vis viva (living force)[2]. A couple of decades later, Gottfried Wilhelm von Leibniz (1646-1716) in 1686 became the first to quantify the concept of vis-viva as the product of mass times the square of the speed.
Thomas Young (1773-1829) did introduce the word energy in 1800 but it did not become a term of common usage at that time. Instead the name “energy” was popularized around fifty years later by William Thomson, Lord Kelvin (1824 – 1907) and William J. M. Rankine (1820-1872) as the concept of force was integrated to act across other related phenomena.
When one looks back at the explosion of European physics that occurred in The Age of Enlightenment and following Leibniz’s vis viva, the concepts linking force and energy, heat[3] and work all helped to lay the foundations for a complete rewrite of the understanding of science away from its Greek origins some two thousand years prior. Eventually these developments led to Albert Einstein’s (1879-1955) rewriting of the Newtonian mechanical universe and arguably the most famous equation in physics equating the relationship between matter and energy:
[latex]E = m c^2[/latex]
Modern day usage of the word “energy” generally causes much confusion in trying to understand and use the concepts of energy in introductory physics classes. The next few sections in this chapter will outline a physical definition of the energy concepts (scalar measures) and how to quantify energy in modern SI metric measures.
Two energy forms, termed “kinetic energy” and “potential energy”, are both classified as forms of mechanical energy.
The first of these, Kinetic Energy[4], is the measure of the energy held by a body in motion. The measure of an object’s kinetic energy is almost identical to that of the vis viva proposed by Leibniz ([latex]mv^2[/latex]) except that it is 1/2 the measure. Energy is often denoted by the capital letter E with a subscript of k to denote that it is the kinetic energy form ([latex]E_k[/latex])[5].
In Newtonian mechanics, the measure of a body’s kinetic energy is given by the equation:
where the mass of the moving object is given in kilograms (kg) and the speed of the object is given in metres per second (m/s). The measure of energy is given the name joules (J) in honour of James Prescott Joule (1818–1889) for his work in his discovery of the mechanical equivalent of heat, which later led to the law of conservation of energy and the development of the First Law of Thermodynamics.
Kinetic Energy can simply be remembered as the energy of a moving body.
The second of the mechanical energies is termed Gravitational Potential Energy (Ep) or its shortened version of Potential Energy[6][7], which is the energy of any object where gravity can accelerate an object through some vertical displacement, and means that the change in position of an object is central. Common examples of gravitational potential energy can be seen in roller coasters, water wheels and in the dams used to create hydroelectric power.
In Newtonian mechanics the measure of a body’s potential energy is given by the equation:
[latex]\Delta E_p=mg\Delta h[/latex] or [latex]E_p = mgh[/latex]
where the mass of the object is given in kilograms (kg), gravity is the strength of gravity for this position measured in metres per second squared (m/s2) and the change in position or height is measured in metres (m). As in kinetic energy, this textbook uses the symbol E to designate energy and the subscript p to indicate that it is potential energy ([latex]E_p[/latex])[8]. The units of measure are the same as used in kinetic energy, joules (J).
Potential Energy can simply be remembered as the energy of a body that can move under the influence of gravity accelerating it.
Gravitational Potential or Gravitational Potential Difference[9] is a concept shared with electricity. You will run into two variations of it in both gravitational and electrical situations. In this first case we only deal with a constant strength gravitational field. Gravitational potential and Electrical potential both use the same symbol ([latex]V[/latex]) named in honor of Alessandro Volta.
Quite simply, gravitational potential in a constant strength gravitational field represents the product of the strength of gravity and change in height. Or… [latex]V = g h[/latex]. If you wish you can use [latex]V_g[/latex] to represent gravitational potential and [latex]V_{el}[/latex] to represent Electrical potential but these are non-standard notations.
You should note that Gravitational Potential [latex]V[/latex] (aka: gravitational potential difference) is close in concept to that of Gravitational Potential Energy [latex]E_p[/latex], with the only difference being that to find the potential energy involved, we must use the mass that is being moved through the potential difference. In this way, in a constant gravitational field, [latex]E_p = m V[/latex] or [latex]m g h[/latex]. The Units for Gravitational Potential are joules/kilogram (J/kg).
Example 10.1.1
What is the average gravitational potential of Niagara Falls, having an average height change before hitting the rocks (hidden by the falls) 53.4 m below?

Solution
Data:
- [latex]V = \text{ Find}[/latex]
- [latex]\Delta h = 53.4 \text{ m}[/latex]
- [latex]g = 9.8 \text{ m/s}^2[/latex]
Solution:
- [latex]V = g \Delta h[/latex]
- [latex]V = (9.8 \text{ m/s}^2)(53.4 \text{ m})[/latex]
- [latex]V = 523 \text{ J/kg}[/latex] (≈ 520 J/kg)
The change in Potential Energy ([latex]\Delta E_p[/latex]) can be calculated using gravitational potential if you have the amount of mass that is moving through the potential difference. You will be using the potential difference concept in much greater detail in the later topics concerning electricity.
The following examples illustrate the equations using the potential and kinetic energy equations.
Example 10.1.2
What is the kinetic energy of a 1250 kg car moving at 90 km/h?
Solution
- [latex]E_k = \frac{1}{2} m v^2[/latex]
- [latex]E_k = \frac{1}{2} (1250 \text{ kg})(25 \text{ m/s})^2[/latex]
- [latex]E_k = 391\;000 \text{ J}[/latex] (≈ 390000 J)
Example 10.1.3
Fifty tonnes of water falls through a height of 3.0 m. What is the change in potential energy for this water?
Solution
- [latex]\Delta E_p = m g \Delta h[/latex]
- [latex]\Delta E_p = (50\;000 \text{ kg})(9.8 \text{ m/s}^2)(3.0 \text{ m})[/latex]
- [latex]\Delta E_p = 1\;470\;000 \text{ J}[/latex] or 1.47 MJ
Example 10.1.4
A 0.500 gram meteor has a momentum of 7.50 Ns. What is its kinetic energy?
Solution
First, find the speed of the meteor:
- [latex]p = m v[/latex] (no vector signs are needed since no direction is given)
- [latex]7.50 \text{ Ns } = (0.5 \times 10^{-3} \text{ kg}) v[/latex]
- [latex]v = 7.50 \text{ Ns } \div 0.5 \times 10^{-3} \text{ kg}[/latex]
- [latex]v = 15\;000 \text{ m/s}[/latex]
Second, find its kinetic energy:
- [latex]E_k = \frac{1}{2} m v^2[/latex]
- [latex]E_k = \frac{1}{2} (0.5 \times 10^{-3} \text{ kg})(15\;000 \text{ m/s})^2[/latex]
- [latex]E_k = 56\;250 \text{ J}[/latex] (≈ 56000 J)
Example 10.1.5
A 7.5 kg mass dropped from a 50 m high bridge changed its velocity from 0 m/s to – 31.3 m/s before striking the ground below. Calculate:
- The change in momentum
Solution- [latex]\vec{p} = m \Delta \vec{v}[/latex] or [latex]m (\vec{v}_f - \vec{v}_i)[/latex]
- [latex]\Delta \vec{p} = (7.5 \text{ kg})(- 31.3 \text{ m/s } - 0 \text{ m/s})[/latex]
- [latex]\Delta \vec{p} = -235 \text{ Ns } (\approx - 230 \text{ Ns})[/latex]
- The change in kinetic energy
Solution- [latex]\Delta E_k = E_{k f} - E_{k i}[/latex]
- [latex]\Delta E_k = \frac{1}{2} (7.5 \text{ kg})(31.3 \text{ m/s})^2 - 0 \text{ J}[/latex]
- [latex]\Delta E_k = 3674 \text{ J } (\approx 3700 \text{ J})[/latex]
- The change in potential energySolution
- [latex]\Delta E_p = E_{p f}[/latex]
- [latex]\Delta E_p = 0 \text{ J } - (7.5 \text{ kg})(9.8 \text{ m/s}^2)(50 \text{ m})[/latex]
- [latex]\Delta E_p = - 3674 \text{ J } (≈ - 3700 \text{ J})[/latex]
Exercise 10.1
- What is the kinetic energy of a 50 kg mass moving at 10 m/s?
- A 1.0 tonne mass is raised through a height of 3.0 m. What is its change in potential energy?
- What is the kinetic energy of an electron (mass [latex]9.11 \times 10^{-31}[/latex]kg) when it is moving at a speed of 1.0 x 107 m/s?
- A 7.5 kg mass has its velocity changed from 15 m/s North to 20 m/s North. Calculate:
- The change in momentum
- The change in kinetic energy
- A 10 gram meteor has a momentum of 7.5 Ns. What is its kinetic energy?
- A child drops 4 identical marbles (0.015 kg) once each second until they are all dropped. After the first marble has fallen for 6.0 s what is the difference in the kinetic energy between the first and the last dropped? (hint… draw a sketch of this)
10.2 Work
- Extra Help: Definition and Mathematics of Work
- Extra Help: Calculating the Amount of Work Done by Forces
Equations Introduced or Used for this Section:
- Work [latex](W) = \vec{F}_{\text{net}} \cdot \vec{d}[/latex] or [latex]\vec{F}_{\text{net}} \vec{d} \cos ø[/latex]
- [latex]w = m g[/latex]
Conceptual Development:
The concept of work is largely accepted as having been introduced by Gaspard-Gustave de Coriolis (1792 – 1843) from his thoughts that work resulted in a transfer of energy by lifting some weight through a distance. These thoughts are believed to have originated from the early use of steam engines used to lift buckets of water out of flooded mines. As such, work was originally defined as the transfer of energy from one place to another or from one form to another. A simple definition of Coriolis’s concept looks like:
[latex]W = \Delta \text{ Energy}[/latex] (or [latex]W = \Delta E_p[/latex])
where energy can be given or extracted from a system by doing work on it. The units of work are joules (J). Often the units newton-metre (Nm) are used as a measure of work but recent movements by academic organizations are acting to discourage this unit due to possible confusion with the concept of Torque, that uses Nm as its measure.
When one looks at the concept of lifting a weight through a height, one is able to define the measure of work using algebra. Specifically: [latex]W = F_{\text{net}} d[/latex] where the net force must be in a direction to change the height of the object.
This means that the Force used must be in the same direction or in the opposite direction to the change in displacement of the object. The angle between the Force vector and the displacement vector must be either 0° or 180°. The equation of [latex]W = F d[/latex] is corrected by the addition of the cosine function of the angle between the force vector and the displacement vector. Specifically:
[latex]W = F_{\text{net}} d \cos ø[/latex] or [latex]W = F_{\text{net}} \cdot d[/latex]
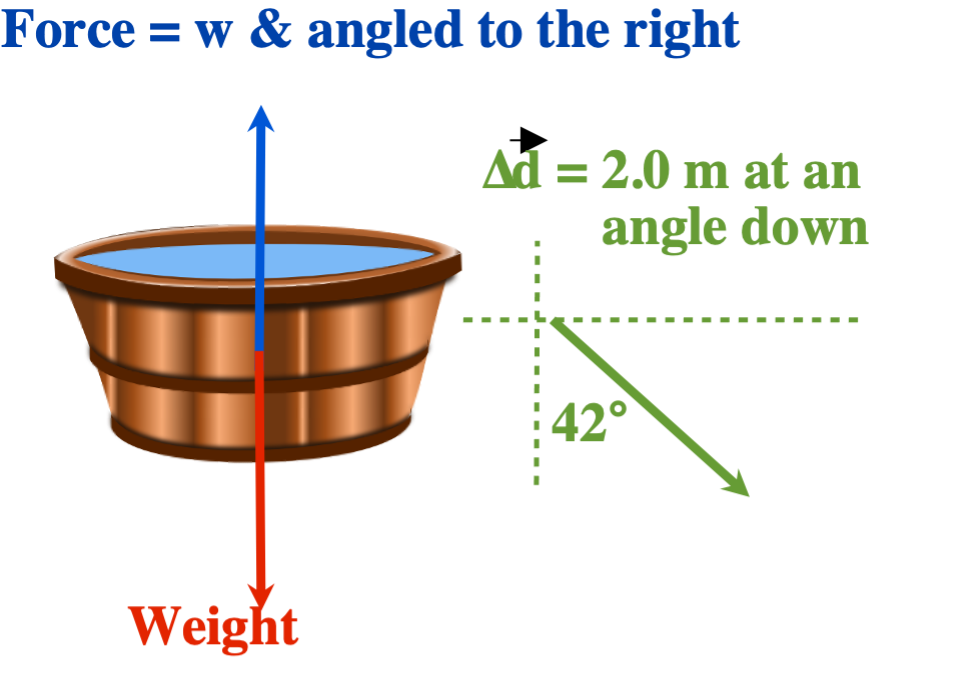
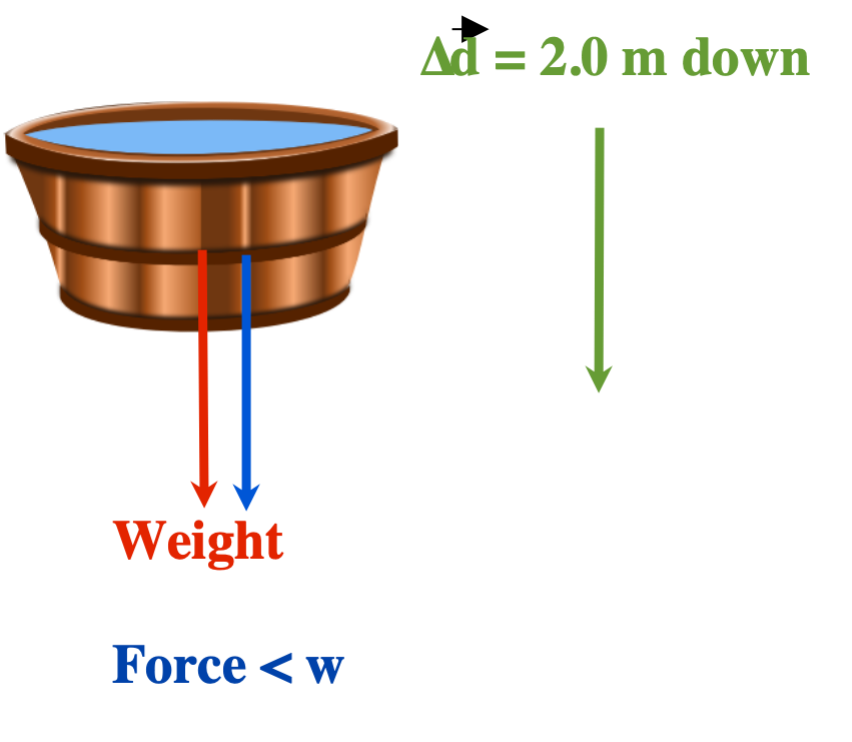
Consider the work done in changing the potential energy of the following tubs of water:
Example 10.2.1
Find the work done changing Ep of a 20 kg tub of water for the following:
- Force upwards balances the weight

- Force upward moves the bucket up 2.0 m and stops

- Force moves the bucket 2.0 m at an angle of 42°upwards and stops

- Force moves the bucket 2.0 m to the side and stops

- Force moves the bucket 2.0 m at an angle of 42° downwards and stops
- Force lowers the bucket 2.0 m down and stops
Example 10.2.2
Find the work done when:
- A force of 10.0 N acts over a distance of 2.0 m
Solution- [latex]W = F d \cos ø[/latex]
- [latex]W = (10 \text{ N})(2.0 \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 20 \text{ J}[/latex]
- A force of 12 µN acts over a distance of 0.55 mm
Solution- [latex]W = F d \cos ø[/latex]
- [latex]W = (12 \times 10^{-6} \text{ N})(0.55 \times 10^{-3} \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 6.6 \times 10^{-9} \text{ J}[/latex]
- A mover lifts a 480 N box of books through a vertical displacement of 5.0 m
Solution- [latex]W = F d \cos ø[/latex]
- [latex]W = (480 \text{ N})(5.0 \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 2400 \text{ J}[/latex]
- 50 kg of water is raised from a well 20 m deep
Solution- [latex]W = F d \cos ø[/latex]
- [latex]W = (50 \text{ kg})(9.8 \text{ m/s}^2)(20 \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 9800 \text{ J}[/latex]
- A stove is slid 2.0 m across a floor against an average resistance of 420 N
Solution- [latex]W = F d \cos ø[/latex]
- [latex]W = (420 \text{ N})(2.0 \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 840 \text{ J}[/latex]
Example 10.2.3
What displacement does a net force of 42 N East need to act over to do 240 J of work?
Solution
- [latex]W = \vec{F} \vec{d} \cos ø[/latex]
- [latex]240 \text{ J } = (42 \text{ N East})(\vec{d}) \cos 0^{\circ}[/latex]
- [latex]\vec{d} = 420 \text{ J } \div 42 \text{ N East}[/latex]
- [latex]\vec{d} = 5.71 \text{ m East } (\approx 5.7 \text{ m East})[/latex]
Example 10.2.4
How much work is done by a net force that resulted in a 20.0 kg mass accelerating at 0.50 m/s2 over a distance of 12 m?
Solution
- [latex]W = F d \cos ø[/latex]
- [latex]W = (20.0 \text{ kg})(0.50 \text{ m/s}^2)(12 \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 120 \text{ J}[/latex]
Exercise 10.2
- Find the work done when:
- A force of 8.0 N acts over a distance of 2.0 m
- A force of 12 N acts over a distance of 55 cm
- A bricklayer lifts a brick weighing 25 N up a vertical displacement of 1.8 m
- 1015 kg of coal is raised from the bottom of a mine 310 m deep
- A box is pushed 10.0 m across a floor with average speed against a 42.0 N resistance
- A force of 17 N South performed 136 J of work. What displacement did the force act over?
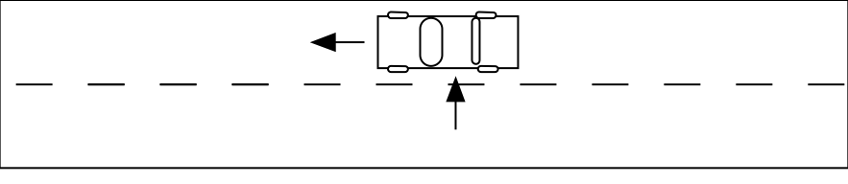
- How much work is done by a force of 105 N (as shown below) if it acts at right angles to the direction this car is moving?
- A girl on a bicycle drags a wagon full of a newspapers at 0.80 m/s for 30 minutes requiring a constant force of 40 N. What amount of work has this child done?
- How much work is done by a force which results in a mass of 30.0 kg having an acceleration of 1.50 m/s2 over a distance of 700 cm?
10.3 Work & Mechanical Energy
- Extra Help: Mechanical Energy
- Extra Help: Internal vs. External Forces
- Extra Help: Gravitational Potential Energy and Work
Equations Introduced or Used for this Section:
- Work [latex](W) = \vec{F}_{\text{net}} \cdot \vec{d}[/latex] or [latex]\vec{F}_{\text{net}} \vec{d} \cos ø[/latex]
- [latex]E_p = m g h[/latex]
- [latex]\Delta E_p = m g \Delta h[/latex]
- [latex]\Delta h = h_f - h_i[/latex]
- [latex]\Delta v = v_f - v_i[/latex]
- [latex]W = \Delta[/latex] Mechanical Energy
- [latex]E_k = \frac{1}{2} m v^2[/latex]
- [latex]\Delta E_k = \frac{1}{2} m \Delta v^2[/latex]
- [latex]V[/latex] or [latex]V_g = g h[/latex]
- [latex]w = m g[/latex]
Summarizing the previous section:
- If the net force is in the same direction as the displacement, then the system gains energy.
- If the net force is in the opposite direction to the displacement, then energy is removed from the system.
- If the net force is at 90° to direction as the change in displacement, then there is no change in the energy of the system.
In this section we investigate the relationship between work and the change in the mechanical energy of a system using [latex]W = \Delta \text{ Mechanical Energy}[/latex]. Using this restriction, we will only be considering changes to potential energy ([latex]\Delta E_p = m g h[/latex]) and kinetic energy ([latex]\Delta E_k = \frac{1}{2}m v^2[/latex]). As before, the force used to change the energy of an object is the net force (and must be conservative) acting on the object which results in some change in the objects displacement, specifically.
Work [latex](W) = \vec{F}_{\text{net}} \cdot \vec{d}[/latex] or [latex]\vec{F}_{\text{net}} \vec{d} \cos ø[/latex]
Net conservative forces[10] are used to define work that acts to change the energy of a body or a system.
The easiest work energy relationship to work with comes from the Work-Energy Theorem, where the work done can be found by the resulting change in an object’s kinetic energy. Specifically:
[latex]W = \Delta E_k[/latex] or [latex]E_{k f} - E_{k i}[/latex]
In this case all one needs to do is to find the change in kinetic energy to calculate the work done.
Expanding on [Work [latex](W) = \vec{F}_{\text{net}} \cdot \vec{d}[/latex] or [latex]\vec{F}_{\text{net}} \vec{d} \cos ø[/latex]], one gets to extend the quantification of force to be either accelerating or braking, and if it is acting at some vertical angle to the change in the object’s displacement.
It is more complicated in defining work as a change in potential energy, since one is restricted to the change in vertical height to calculate this change. For instance, if an object is raised and lowered several times but ends up in the initial position at the end of this event, then [latex]\Delta E_p = 0 \text{ J}[/latex] even though a lot of energy was expended in raising and lowering the object. Changes in potential energy are path dependent.
For the [latex]W = \Delta E_k[/latex] to be correct in usage for these problems, the force acting must be a conservative force, where the only changes in energy are either potential (and kinetic). As you advance in your physics studies, you will be required to distinguish between conservative forces and non-conservative forces.
The derivation of the kinetic energy equation can be completed using an equation termed the work-energy theorem, specifically [latex]W = \Delta E_k[/latex] and the angle between the force and displacement ø = 0°.
First:
[latex]W = \Delta[/latex] Energy where [latex]W = \vec{F}_{\text{net}} \cdot \vec{d}[/latex] & [latex]\vec{F}_{\text{net}} = m a (d)[/latex]
Yielding:
[latex]\Delta \text{ Energy } = m a d[/latex]
Using the kinematic equation...
- [latex]2 a d = v_f^2 - v_i^2[/latex]
- [latex]a d = \dfrac{(v_f^2 - v_i^2)}{2}[/latex]
Substituting into the first equation [latex]\Delta \text{ Energy } = m a d[/latex], we get
[latex]\Delta E = \dfrac{(v_f^2 - v_i^2)}{2}[/latex]
And is generally written as:
[latex]E_k = \frac{1}{2} m v^2[/latex]
The derivation of potential energy has two versions: one for a constant gravitational field strength and the second (which is covered later) for a variable gravitational field where one has a change in gravity as one moves away (or towards) a planet, sun or moon.
The derivation of the potential energy equation can also be done using the work-energy theorem., specifically [latex]\Delta \text{ Energy } = W[/latex] or ([latex]F_{\text{net}} d \cos ø[/latex] or [latex]magd[/latex]) and requires the acceleration of gravity affecting the body is constant and the angle between the net force and the change in vertical displacement is ø = 0°. This derivation is easily completed.
First:
[latex]W = \Delta \text{ Energy}[/latex] where [latex]W = \vec{F}_{\text{net}} \cdot d[/latex] & [latex]\vec{F}_{\text{net}} = m a (d)[/latex]
Yielding:
[latex]\Delta \text{ Energy } = m a d[/latex]
Replace “a” with the constant acceleration due to gravity and “d” with the vertical change in height.
This results in:
[latex]\Delta \text{ Energy } = m g \Delta h[/latex]
And is generally written as:
[latex]E_p = m g h[/latex]
Example 10.3.1
How much work is done by an electric pump which raises 200 kg of water for irrigation through a vertical distance of 150 m?
Solution
- [latex]W = \Delta E_p[/latex]
- [latex]W = (200 \text{ kg})(9.8 \text{ m/s}^2)(150 \text{ m}) \cos 0^{\circ}[/latex]
- [latex]W = 294\;000 \text{ J}[/latex] (≈ 290000 J)
Example 10.3.2
How much work is done in raising a 1500 kg pile driver through a potential difference of 400 N/kg?
Note: Potential difference ([latex]V[/latex]) represents the product of [latex]g h[/latex]
Solution
- [latex]W = \Delta E_p[/latex] where [latex]\Delta E_p = m g h[/latex] or [latex]m V[/latex]
- [latex]W = (1500 \text{ kg})(400 \text{ N/kg}) \cos 0^{\circ}[/latex]
- [latex]W[/latex] = 600000 J
Example 10.3.3
Through what distance must a 4.00 tonne pile driver fall to do 500 kJ of work?
Solution
- [latex]W = \Delta E_p[/latex]
- [latex]500 \text{ kJ } = (4000 \text{ kg})(9.8 \text{ m/s}^2) d \cos 0^{\circ}[/latex]
- [latex]d = 500\;000 \text{ J } \div 39\;200 \text{ kg m/s}^2[/latex]
- [latex]d = 12.8 \text{ m } (\approx 13 \text{ m})[/latex]
Example 10.3.4
At what speed must a 400 kg pile driver be falling to do 15000 J of work?
Solution
- [latex]W = \Delta E_k[/latex]
- [latex]15\;000 \text{ J } = \frac{1}{2} (400 \text{ kg}) v^2[/latex]
- [latex]v^2 = 15\;000 \text{ J } \div 200 \text{ kg}[/latex]
- [latex]v = 8.66 \text{ m/s } (\approx 8.7 \text{ m/s})[/latex]
Example 10.3.5
How much work is needed to stop a truck that has 400 kJ of kinetic energy in 10 s in a distance of 50 m?
Solution
Since work = Energy and the truck has 400 kJ of kinetic Energy, the work done is:
- [latex]W = E_{k f} - E_{ k i}[/latex]
- [latex]W = 0 \text{ J } - 400 \text{ kJ } = -400\;000 \text{ J}[/latex]
The minus sign means that 400000 J of energy was extracted from the truck.
Example 10.3.6
A semi-truck has 4.0 MJ of kinetic energy. What braking force would bring it to a full stop in a distance of 500 m?
Solution
First the work done is extracting 4.0 MJ energy from the truck, therefore
- [latex]W = F d \cos ø[/latex]
- [latex]- 4.0 \text{ MJ } = F (500 \text{ m})\cos 0^{\circ}[/latex]
- [latex]F = - 4\;000\;000 \text{ J} \div 500 \text{ m or } - 8000 \text{ N}[/latex]
Example 10.3.7
A commercial jet (mass 80000 kg) lands on a horizontal runway at 165 km/h. If it decelerates through a displacement of 1200 m before coming to a full stop, calculate the average net force exerted by its brakes.
Solution
First:
- [latex]W = \Delta \text{ Energy}[/latex], where the change in energy is the kinetic energy of the jet.
Therefore:
- [latex]W = \Delta E_k[/latex] (or [latex]E_{k f} - E_{k i}[/latex]) where [latex]E_{k f} = 0 \text{ J}[/latex]
Expanded, this equals:
- [latex]F d \cos ø = 0 \text{ J } - \frac{1}{2} m v^2[/latex]
- [latex]F d \cos ø = 0 \text{ J } - \frac{1}{2} m v^2[/latex]
- [latex]F (1200 \text{ m}) \cos 0^{\circ} = - \frac{1}{2} (80\;000 \text{ kg})(45.8 \text{ m/s}^2)[/latex]
- [latex]F = - 70\;000 \text{ N}[/latex]
The negative in the solution for 9.36 and 9.37 means that energy is being extracted from the system or that negative work is being done on these systems.
Exercise 10.3
- A 50.0 g cannon shell is traveling at 700 m/s at a height of 2.50 km. Calculate its:
- Kinetic Energy
- Potential Energy
- Total Mechanical Energy
- How much work is done by a pump that raises 2.0 metric tonnes of water through a vertical distance of 50 m?
- How much work is done in raising 100.0 kg through a potential difference of 196 N/kg?
- Through what potential difference must a 400 kg pile driver fall to do 15000 J of work?
- How much work is needed for a 100 kg person to reach a speed of 10 m/s from rest?
- How much work is needed to stop a 1400 kg truck traveling at 100 km/h?
- What average braking force is required to stop a 2 tonne truck traveling at 80 km/h in 200 m?
- A 60 kg softball player slides into home plate going from 9.5 m/s to a full stop in 2.5 m. What average force acts on this player?
- How much work is needed to slow a 5.8 kg mass from a speed of 2.3 m/s to 1.5 m/s?
- A bullet (mass 1.75 g) is fired at 125 m/s into a thick block of wood where it comes to rest. How much work did this bullet do on the block of wood?
- An 80.0 g mass is fired at a wall with a horizontal velocity of 130 m/s and emerges at 65 m/s. How much work was done in piercing this wall?
- An airplane (mass 2400 kg) lands on a horizontal runway at 50 m/s. If it decelerates through a displacement of 180 m before coming to a full stop. Calculate the average force exerted by these brakes.
- A truck has 200 KJ of kinetic energy. What braking force would bring it to a full stop in a distance of 250 m?
- A 2.0 g bullet is shot into a tree stump. It enters at a speed of 300 m/s and comes to rest after penetrating 5.0 cm in a straight line. What was the average force acting on this bullet during the impact and how much work did this bullet do?
- A truck of mass 2.0 tonnes is moving at 20 m/s. Calculate:
- Its kinetic energy
- The force needed to stop it in 10 s
- The force needed to stop it in 100 m.
- A 1200 kg car is traveling at 25 m/s at the top of a 60 m high hill before it starts to descend. At the base of the hill the brakes are applied with an average force of 8000 N. What distance is required to bring this car to a full stop?
Exercise 10.4.1: Bennu on JPL’s Sentry: Earth Monitoring List
NASA has a program that monitors the orbits of Near-Earth Objects (NEOs) as part of its support of NASA’s Planetary Defense Coordination Office. NEO objects (mainly asteroids) are analyzed and classified according to their orbital parameters, close approaches to Earth, and impact risks, along with other factors that record their discovery and possible mission. Sentry is a special list of potentially hazardous NEOs that pose a threat from possible impact with the Earth. Considered to be the most dangerous are the asteroids 29075 1950DA having a diameter of 2000 m, with a 1/8300 chance of impact in 2880-03-16, 410777 2009FD having a diameter of 150 m, with a 1/710 chance of impact in 2185-03-29 and 101955 Bennu having a diameter of 484 m, with a 1/2700 chance of impact between 2175 and 2199. Of these three 29074 1950DA is considered to be the greatest risk to Earth and 101955 Bennu to be of the second greatest known risk.
101955 Bennu or simply Bennu (named after the Egyptian mythological bird Bennu) has an average diameter of close to 1/2 km (492 m) and orbits the Sun every 1.20 yr (436.65 d) traveling an average 12.1 km/s. It has an estimated mass of 7.329 ± 0.009 x 1010 kg with an average density of 1.26 ± 0.013 x 103 kg/m3 indicating a density that is slightly greater than water. Close analysis indicates Bennu to be basically a big ball of rubble varying in size from mm up to one observed 20 m boulder. However, the energy released from an impact with the Earth is estimated to be in the range of 1200 megatons of TNT (roughly 80000 times that of the nuclear weapon dropped on Hiroshima in World War II).

Question:
- Using the estimated mass and average speed for Bennu, calculate the kinetic energy that would be released during a collision with Earth.
- How does this compare with the estimated 1200 megaton value of TNT that would be released?
Note: 1 kg of TNT releases [latex]4.184 \times 10^6[/latex] J
Exercise Answers
10.1 Kinetic and Potential Energy
- 2500 J
- [latex]2.9 \times 10^4[/latex] J
- [latex]4.56 \times 10^{-17}[/latex] J
-
- 38 Ns North
- 660 J
- 2800 J
- − 19 J
10.2 Work
-
- 16 J
- 6.6 J
- 45 J
- [latex]3.08 \times 10^6[/latex] J
- 420 J
- 8.0 m South
- Zero joules, (0 J)
- 58000 J
- 320 J
10.3 Work & Mechanical Energy
-
- [latex]1.225 \times 10^3[/latex] J
- [latex]1.225 \times 10^4[/latex] J
- [latex]1.35 \times 10^4[/latex] J
- [latex]9.8 \times 10^5[/latex] J
- 19600 J
- 37.5 N/kg
- 5 000 J
- − 540000 J
- − 2500 N
- − 1100 N
- − 2500 N
- − 13.7 J
- − 510 J
- 17000 N
- 800 N
-
- − 1800 N
- − 90 J
-
- [latex]4.0 \times 10^5[/latex] J
- − 4000 N
- − 4000 N
- 140 m
10.4.1 Bennu on JPL’s Sentry: A Potential Major Natural Disaster
- [latex]E_k = 5.37 \times 10^{18}[/latex] J
- 1300 mega tons of TNT
Media Attributions
- "Niagara Falls" by martajozsa is licensed under a Pixabay licence.
- "Bennuasteroid" from NASA is in the public domain.
- Leibniz‘s Vis Viva (mv2) is what we now know to be twice the kinetic energy of a body ↵
- Vis viva was also named as the tensional force and fall force. ↵
- Galileo’s creation of the thermometer in the early 1590s was essential to the understanding of the relationship between heat and energy. Joseph Black’s studies on heat (1728 - 1799) were what has been credited as the inspiration for James Watt’s (1736-1819) building of the first modern steam engine and as such, the start of the industrial revolution. ↵
- Kinetic is derived from its Greek root kinesis, meaning movement or motion. ↵
- There are multiple forms of the symbol representing kinetic energy ... Ek, KE, K and T. ↵
- There are three more forms of potential energy that are commonly used by physicists: Electromagnetic Potential Energy (electric potential energy, magnetic potential energy, chemical potential energy and elastic potential energy), Strong Nuclear Potential Energy (nuclear power, nuclear weapons) and Weak Nuclear Potential Energy (radioactive decay). Source: https://physics.info/energy/ ↵
- William Rankine is credited to be the originator of the name “potential energy” in 1853. ↵
- There are multiple forms of the symbol representing potential energy... Ep, PE, P and U. ↵
- Do not confuse this terminology with Gravitational Potential Energy. ↵
- When looking at work acting to change the mechanical energy of a system, there is a need to define forces as conservative and non-conservative (for reasons similar to that of the need for scalar and vector measurements). Conservative Forces are path-independent and work done to change an object’s potential energy is by forces such as gravity (acting straight down). Non-conservative Forces are path-dependent and the amount of work done depends on the path. For non-conservative forces such as air resistance and friction become examples of how energy is lost or dissipated in moving an object from one place to another. This means that if a system is acted upon by non-conservative forces (any type of a frictional force) then not all the work will result in a change of the mechanical energy of a system. ↵

