Math for Medication Administration
14 Calculating Medication Dosage
Lesson
Learning Outcomes
By the end of this chapter, learners will be able to:
- explain a method for solving medication dose problems, and
- correctly solve medication dose problems.
There are often multiple ways to solve problems involving math. In this workbook, the process of dimensional analysis is presented as one way to solve all types of medication related problems. You can continue to use this process when solving practice problems presented in this chapter. Using this form of problem solving can help you reduce errors if you struggle to remember formulas or figure out which formula to use as you can learn just one method to approach all the calculations.
Steps to Calculate Medication Amounts
- Read the information carefully. Avoid distractions when preparing medications so you can focus on the problem at hand. What information are you trying to calculate?
- Set up the formula. When beginning to calculate medication amounts it is helpful to always write down your work so you can check your work and so others can help you find errors if you have made a mistake.
- Calculate the answer by using a calculator or mental math.
- Check your work. Always double check your answer. Does it make sense? If you have determined you need to give 20 tablets for one dose this would be a red flag-an unlikely situation and indicates an error has probably been made. As a student, you should always have a supervising nurse check your math. After you graduate, there are specific high risk medications (like insulin) which must be double checked by another nurse. You may also decide that specific situations warrant asking someone to check, such as if you have been feeling tired or if there are distractions during your process of medication administration.
Sample Exercise 14.1: Determining the number of tablets required when the dose is more than the supply
How many tablets would you administer for the following medication order?
Order: prednisone 20 mg PO OD
Supply: prednisone 5 mg tablets
Answer:
4 tablets.
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{5 mg}}\times{\text{20mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{5\cancel{\text{ mg}}}\times{20\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{20 tablet}}{5}\\[/latex][latex]\text{x tablets}=4[/latex]
Alternate Formula for Solving Medication Dose Problems
[latex]\dfrac{\text{Desired amount}}{\text{Amount in supply}}\times{\text{Volume of supply}}=\text{Quantity for dose}[/latex]
This may also be written as:
[latex]\dfrac{\text{Desired Amount}}{\text{Dose on hand}}\times{\text{Volume}}=\text{Dose}[/latex]
Or abbreviated as:
[latex]\dfrac{\text{D}}{\text{H}}\times{\text{V}}=\text{Dose}[/latex]
Regardless of the words or letters chosen to represent numbers in the formula, the numbers related to the medication problem are always in the same place.
Here is the same problem from the sample exercise above, using this formula:
Order: prednisone 20 mg PO OD
Supply: prednisone 5 mg tablets
[latex]\dfrac{\text{Desired amount}}{\text{Amount in supply}}\times{\text{Volume of supply}}=\text{Quantity for dose}\\[/latex][latex]\dfrac{\text{20 mg}}{\text{5 mg}}\times{\text{1 tablet}}=\text{Quantity for dose}\\[/latex][latex]\dfrac{20\cancel{\text{ mg}}}{5\cancel{\text{ mg}}}\times{\text{1 tablet}}=\text{Quantity for dose}\\[/latex][latex]4\text{ tablets}\\[/latex]
Make sure to check your work:
- First, check your formula and make sure it has been set up correctly.
- Do all of the units cancel out based on the way you have set up the formula? If you are not left with units matching on both sides of the equals sign, this is a clue information has been put into the formula incorrectly.
- Next, look for calculation errors by doing the math again to see if you get the same answer.
- Lastly, have a supervising nurse confirm you have calculated the correct amount.
Sample Exercise 14.2: Determining the number of tablets required when the dose is less than the supply
How many tablets would you administer for the following medication order?
Order: metoprolol 12.5 mg PO BID
Supply: metoprolol 50 mg tablets
Answers:
0.25 of one tablet, or [latex]\dfrac{1}{4}\\[/latex]
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{50 mg}}\times{\text{12.5mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{50\cancel{\text{ mg}}}\times{12.5\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{12.5 tablet}}{\text{50}}\\[/latex][latex]\text{x tablets}=0.25[/latex]
Sample Exercise 14.3: Determining the volume of medication required
What volume needs to be drawn up to administer the following medication?
Order: dimenhydrinate 25 mg SC prn q6h
Supply: dimenhydrinate 50 mg/mL
Answers:
0.5 mL
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{50 mg}}\times{\text{25 mg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{50\cancel{\text{ mg}}}\times{25\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{25 mL}}{\text{50}}\\[/latex][latex]\text{x mL}=0.5[/latex]
Key Takeaways
When calculating dosages, follow the following steps:
- Read the information presented carefully
- Set up the formula
- Ensure units cancel out
- Calculate the amount required
- Check your work
Practice Set 14.1: Calculating the Number of Tablets
Practice Set 14.1: Calculating the number of tablets to administer
Calculate how many tablets would you administer for the following medication orders. Click on the word answers to check your work.
Questions:
- Order: acetaminophen 650 mg PO QID
Supply: acetaminophen 325 mg tablets - Order: sertraline 75 mg PO OD
Supply: sertraline 25 mg capsules - Order: ibuprofen 400 mg PO QID prn
Supply: ibuprofen 200 mg tablets - Order: dimenhydrinate 12.5 mg PO QID prn
Supply: dimenhydrinate 50 mg tablets - Order: gabapentin 300 mg PO OD
Supply: gabapentin 100 mg capsules - Order: azithromycin 1 g PO
Supply: azithromycin 250 mg tablets - Order: digoxin 250 mcg PO OD
Supply: digoxin 0.5 mg tablets - Order: furosemide 80 mg PO OD
Supply: furosemide 40 mg tablets - Order: glyburide 10 mg PO BID
Supply: glyburide 5 mg tablets - Order: diltiazem 45 mg PO BID
Supply: diltiazem 90 mg tablets
Answers:
- 2 tablets
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{325 mg}}\times{\text{650mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{325\cancel{\text{ mg}}}\times{650\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{650 tablet}}{\text{325}}\\[/latex][latex]\text{x tablets}=2[/latex] - 3 capsules
[latex]\text{x tablets}=\dfrac{\text{1 capsule}}{\text{25 mg}}\times{\text{75 mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 capsule}}{25\cancel{\text{ mg}}}\times{75\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{75 capsule}}{\text{25}}\\[/latex][latex]\text{x tablets}=3[/latex] - 2 tablets
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{200 mg}}\times{\text{400mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{200\cancel{\text{ mg}}}\times{400\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{400 tablet}}{\text{200}}\\[/latex][latex]\text{x tablets}=2[/latex] - 0.25 tablet
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{50 mg}}\times{\text{12.5 mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{50\cancel{\text{ mg}}}\times{12.5\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{12.5 tablet}}{\text{50}}\\[/latex][latex]\text{x tablets}=0.25[/latex] - 3 capsules
[latex]\text{x tablets}=\dfrac{\text{1 capsule}}{\text{100 mg}}\times{\text{300 mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 capsule}}{100\cancel{\text{ mg}}}\times{300\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{300 capsule}}{\text{100}}\\[/latex][latex]\text{x tablets}=3[/latex] - 4 tablets
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{250 mg}}\times{\dfrac{\text{1000 mg}}{\text{1 g}}}\times{\text{1 g}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{250\cancel{\text{ mg}}}\times{\dfrac{1000\cancel{\text{ mg}}}{\cancel{\text{1 g}}}}\times{\cancel{\text{1 g}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1000 tablet}}{\text{250}}\\[/latex][latex]\text{x tablets}=4[/latex] - 0.5 tablet
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{0.5 mg}}\times{\dfrac{\text{1 mg}}{\text{1000 mcg}}}\times{\text{250 mcg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{0.5\cancel{\text{ mg}}}\times{\dfrac{1\cancel{\text{ mg}}}{1000\cancel{\text{ mcg}}}}\times{250\cancel{\text{ mcg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{250 tablet}}{\text{500}}\\[/latex][latex]\text{x tablets}=0.5[/latex] - 2 tablets
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{40 mg}}\times{\text{80 mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{40\cancel{\text{ mg}}}\times{80\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{80 tablet}}{\text{40}}\\[/latex][latex]\text{x tablets}=2[/latex] - 2 tablets
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{5 mg}}\times{\text{10 mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{5\cancel{\text{ mg}}}\times{10\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{10 tablet}}{5}\\[/latex][latex]\text{x tablets}=2[/latex] - 0.5 tablet
[latex]\text{x tablets}=\dfrac{\text{1 tablet}}{\text{90 mg}}\times{\text{45 mg}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{1 tablet}}{90\cancel{\text{ mg}}}\times{45\cancel{\text{ mg}}}\\[/latex][latex]\text{x tablets}=\dfrac{\text{45 tablet}}{\text{90}}\\[/latex][latex]\text{x tablets}=0.5[/latex]
Practice Set 14.2: Calculating the Volume of a Medication Dose
Practice Set 14.2: Calculating the volume of a medication dose
Calculate the volume of liquid you would draw up for the following medication orders. Click on the word answers to check your work.
Questions:
- Order: 25 mg dimenhydrinate IV q6h prn

- Order: hydromorphone 1.5 mg SC q4h prn

- Order: 7 mg diazepam IM now

- Order: gentamycin 112 mg IV q8h
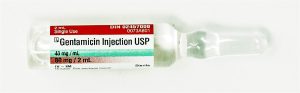
- Order: hydromorphone 0.5 mg SC q4-6 h prn

- Order: 50 mcg cyanocobalamin SC OD x 7 days
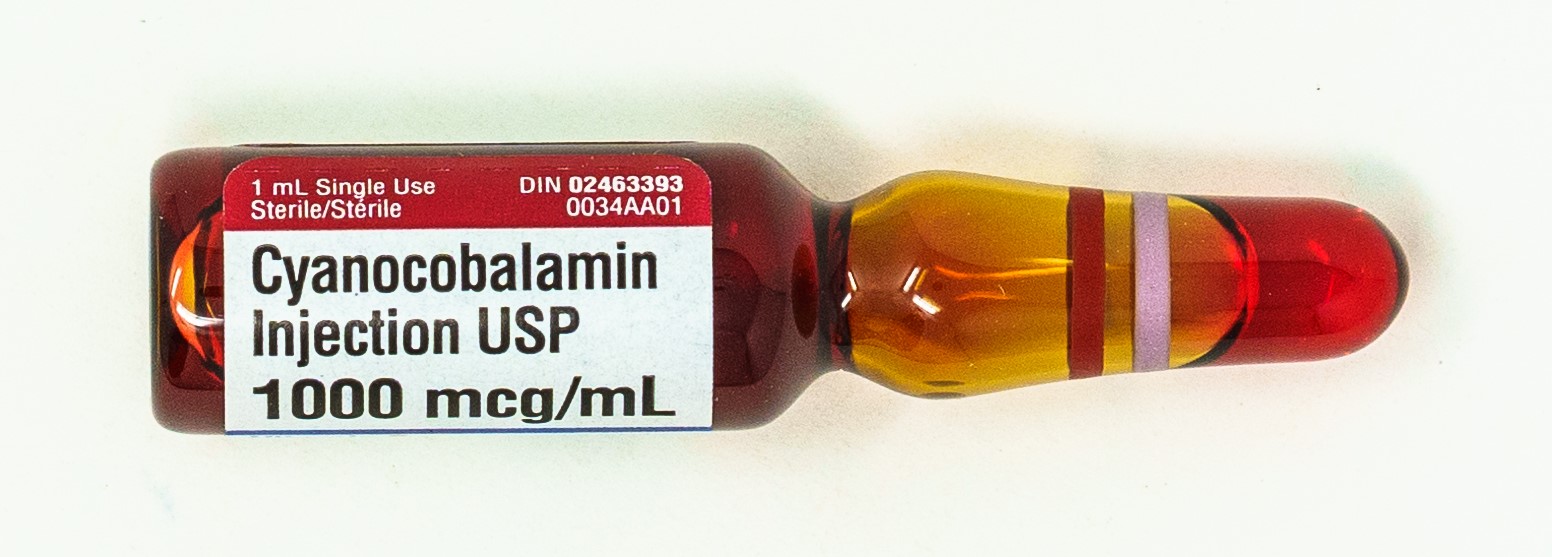
- Order: digoxin 10 mcg/kg IV total loading dose; administer 50% initially; then give ¼ the loading dose q8hr twice. Client weighs 74 kg
How much would you draw up for the first dose of digoxin?

Answers:
- 0.5 mL
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{50 mg}}\times{\text{25 mg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{50\cancel{\text{ mg}}}\times{25\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{25 mL}}{\text{50}}\\[/latex][latex]\text{x mL}=0.5[/latex] - 0.75 mL
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{2 mg}}\times{\text{1.5 mg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{2\cancel{\text{ mg}}}\times{1.5\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1.5 mL}}{2}\\[/latex][latex]\text{x mL}=0.75[/latex] - 1.4 mL
[latex]\text{x mL}=\dfrac{\text{2 mL}}{\text{10 mg}}\times{\text{7 mg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{2 mL}}{10\cancel{\text{ mg}}}\times{7\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{15 mL}}{10}\\[/latex][latex]\text{x mL}=1.4[/latex] - 2.8 mL
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{40 mg}}\times{\text{112 mg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{40\cancel{\text{ mg}}}\times{112\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{112 mL}}{\text{40}}\\[/latex][latex]\text{x mL}=2.8[/latex] - 0.25 mL
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{2 mg}}\times{\text{0.5 mg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{2\cancel{\text{ mg}}}\times{0.5\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{0.5 mL}}{2}\\[/latex][latex]\text{x mL}=0.25[/latex] - 0.05 mL
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{1000 mcg}}\times{\text{50 mcg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{1000\cancel{\text{ mg}}}\times{50\cancel{\text{ mg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{50 mL}}{\text{1000}}\\[/latex][latex]\text{x mL}=0.05[/latex] - 1.48 mL
First, calculate the total loading dose based on the client’s weight.
[latex]\text{x mcg}=\dfrac{\text{10 mcg}}{\text{1 kg}}\times{\text{74 kg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{10 mcg}}{1\cancel{\text{ kg}}}\times{74\cancel{\text{ kg}}}\\[/latex][latex]\text{x mL}=740\text{ mcg}\\[/latex]
Second, calculate the amount of the first portion of the loading dose. (50% = half of the total)
[latex]740\text{ mcg}\div 2[/latex]
[latex]=370\text{ mcg}[/latex]
Third, calculate the volume to draw up from the medication supply.
[latex]\text{x mL}=\dfrac{\text{1 mL}}{\text{0.25 mg}}\times\dfrac{\text{1 mg}}{\text{1000 mcg}}\times{\text{370 mcg}}\\[/latex][latex]\text{x mL}=\dfrac{\text{1 mL}}{0.25\cancel{\text{ mg}}}\times\dfrac{1\cancel{\text{ mg}}}{1000\cancel{\text{ mcg}}}\times{370\cancel{\text{ mcg}}}\\[/latex][latex]\text{x mL}=\dfrac{\text{370 mL}}{\text{250}}\\[/latex][latex]\text{x mL}=1.48\text{ mL}[/latex]
Practice Set 14.3: Calculating the Volume of a Medication Dose and Selecting the Correct Syringe Size
Practice Set 14.3: Calculating the Volume of a Medication Dose and Selecting the Correct Syringe Size
Calculate the volume of liquid you would draw up for the following medication orders. Look at the images and drag and drop an image of a syringe filled with the correct volume into the empty rectangle on the right. Click on the word check to see if you have selected a syringe with the correct volume. Click on the word answers to check your work for the medication math.
Questions:
Answers:
- 0.65 mL
[latex]\begin{align*} \dfrac{65}{x} &=\dfrac{100}{1} \\ \\ 65 &=\text{(100)(x)} \\ \\ 0.65 &=\text{x}\end{align*}[/latex] - 1.2 mL
[latex]\begin{align*} \dfrac{120}{x} &=\dfrac{300}{3} \\ \\ 360 &=\text{(300)(x)} \\ \\ 1.2 &=\text{x}\end{align*}[/latex] - 0.5 mL
[latex]\begin{align*} \dfrac{0.5}{x} &=\dfrac{1}{1} \\ \\ 0.5 &=\text{(1)(x)} \\ \\ 0.5 &=\text{x}\end{align*}[/latex] - 2.25 mL
[latex]\begin{align*} \dfrac{4.5}{x} &=\dfrac{2}{1} \\ \\ 4.5 &=\text{(2)(x)} \\ \\ 2.25 &=\text{x}\end{align*}[/latex] - 0.7 mL
[latex]\begin{align*} \dfrac{35}{x} &=\dfrac{50}{1} \\ \\ 35 &=\text{(50)(x)} \\ \\ 0.7 &=\text{x}\end{align*}[/latex] - 0.7 mL
[latex]\begin{align*} \dfrac{3.5}{x} &=\dfrac{5}{1} \\ \\ 3.5 &=\text{(5)(x)} \\ \\ 0.7 &=\text{x}\end{align*}[/latex] - 0.35 mL
[latex]\begin{align*} \dfrac{1.4}{x} &=\dfrac{4}{1} \\ \\ 1.4 &=\text{(4)(x)} \\ \\ 0.35 &=\text{x}\end{align*}[/latex] - 0.53 mL
[latex]\begin{align*} \dfrac{1.6}{x} &=\dfrac{6}{2} \\ \\ 3.2 &=\text{(6)(x)} \\ \\ 0.53 &=\text{x}\end{align*}[/latex] - 1.8 mL
[latex]\begin{align*} \dfrac{7.2}{x} &=\dfrac{4}{1} \\ \\ 7.2 &=\text{(4)(x)} \\ \\ 1.8 &=\text{x}\end{align*}[/latex] - 1.7 mL
[latex]\begin{align*} \dfrac{0.17}{x} &=\dfrac{0.1}{1} \\ \\ 0.17 &=\text{(0.1)(x)} \\ \\ 1.7 &=\text{x}\end{align*}[/latex]
Practice Set 14.4: Calculating the Volume of a Medication Dose and Selecting the Correct Syringe Size
Practice Set 14.4: Calculating the Volume of a Medication Dose and Selecting the Correct Syringe Size
Calculate the volume of liquid you would draw up for the following medication orders. Look at the images and determine which syringes filled with liquid represent the correct volume of medication. There may be more than one correct syringe size option. Drag and drop all syringes with correct volumes into the open rectangle on the right. Click on the word check to see if your selection is correct. Click on the word answers to see the work for the medication math.
Questions:
Answers:
- 2 mL
[latex]\begin{align*} \dfrac{0.4}{x} &=\dfrac{0.2}{1} \\ \\ 0.4 &=\text{(0.2)(x)} \\ \\ 2 &=\text{x}\end{align*}[/latex] - 0.2 mL
[latex]\begin{align*} \dfrac{20}{x} &=\dfrac{300}{3} \\ \\ 60 &=\text{(300)(x)} \\ \\ 0.2 &=\text{x}\end{align*}[/latex] - 0.4 mL
[latex]\begin{align*} \dfrac{50}{x} &=\dfrac{125}{1} \\ \\ 50 &=\text{(125)(x)} \\ \\ 0.4 &=\text{x}\end{align*}[/latex] - 0.6 mL
[latex]\begin{align*} \dfrac{24}{x} &=\dfrac{40}{1} \\ \\ 24 &=\text{(40)(x)} \\ \\ 0.6 &=\text{x}\end{align*}[/latex] - 0.75 mL
[latex]\begin{align*} \dfrac{3}{x} &=\dfrac{4}{1} \\ \\ 3 &=\text{(4)(x)} \\ \\ 0.75 &=\text{x}\end{align*}[/latex] - 0.27 mL
[latex]\begin{align*} \dfrac{0.27}{x} &=\dfrac{1}{1} \\ \\ 0.27 &=\text{(1)(x)} \\ \\ 0.27 &=\text{x}\end{align*}[/latex] - 0.8 mL
[latex]\begin{align*} \dfrac{4}{x} &=\dfrac{5}{1} \\ \\ 4 &=\text{(5)(x)} \\ \\ 0.8 &=\text{x}\end{align*}[/latex] - 2.5 mL
[latex]\begin{align*} \dfrac{300}{x} &=\dfrac{120}{1} \\ \\ 300 &=\text{(120)(x)} \\ \\ 2.5 &=\text{x}\end{align*}[/latex] - 2.6 mL
[latex]\begin{align*} \dfrac{5.2}{x} &=\dfrac{2}{1} \\ \\ 5.2 &=\text{(2)(x)} \\ \\ 2.6 &=\text{x}\end{align*}[/latex] - 2 mL
[latex]\begin{align*} \dfrac{25}{x} &=\dfrac{12.5}{1} \\ \\ 25 &=\text{(12.5)(x)} \\ \\ 2 &=\text{x}\end{align*}[/latex]
Practice Set 14.5: Calculating the Volume of a Medication Dose and Selecting the Correct Syringe Size
Practice Set 14.5: Calculating the Volume of a Medication Dose and Selecting the Correct Syringe Size
Calculate the volume of liquid you would draw up for the following medication orders. Look at the images and determine which syringes filled with liquid represent the correct volume of medication. There may be more than one correct syringe size option. Drag and drop all syringes with correct volumes into the open rectangle on the right. Click on the word check to see if your selection is correct. Click on the word answers to see the work for the medication math.
Questions:
- A patient exposed to an STI receives an order of ceftriaxone.
- A pediatric patient is requiring a dose of glycopyrrolate.
- A patient with an infection requires a dose of ampicillin.
- A pediatric patient has an anaphylactic reaction to a medication and pre-filled syringes are out of stock. Draw up the ordered dose of epinephrine. After the patient stabilizes, draw up diphenhydramine for IM injection.
- A physician has ordered dexamethasone for you to draw up and administer for a pediatric patient with cerebral edema.
- You are drawing up heparin for a pediatric patient’s loading dose for heparinization.
- A prophylactic dose of gentamicin is required for a pre-surgical adult patient weighing 53 kg.
- A child arrives to the emergency department with a fractured arm and requires morphine for acute pain.
- A 45-year-old with right-sided flank pain requires analgesic.
- You are caring for a 73-year-old with pulmonary edema.
Answers:
- 2.2 mL
[latex]\begin{align*} \dfrac{785}{x} &=\dfrac{250}{0.7} \\ \\ 549.5 &=\text{(250)(x)} \\ \\ 2.2 &=\text{x}\end{align*}[/latex] - 1.8 mL
[latex]\begin{align*} x\text{ mg} &=\dfrac{\text{1 mg}}{1000\cancel{\text{mcg}}}\times360\cancel{\text{ mcg}} x &=\text{0.36 mg}\end{align*}[/latex]
[latex]\begin{align*} \dfrac{0.36}{x} &=\dfrac{0.2}{1} \\ \\ 0.36 &=\text{(0.2)(x)} \\ \\ 1.8 &=\text{x}\end{align*}[/latex] - 1.7 mL
[latex]\begin{align*} \dfrac{425}{x} &=\dfrac{500}{2} \\ \\ 850 &=\text{(500)(x)} \\ \\ 1.7 &=\text{x}\end{align*}[/latex] - 0.45 mL
[latex]\begin{align*} \dfrac{0.45}{x} &=\dfrac{1}{1} \\ \\ 0.45 &=\text{(1)(x)} \\ \\ 0.45 &=\text{x}\end{align*}[/latex]
0.7 mL
[latex]\begin{align*} \dfrac{35}{x} &=\dfrac{50}{1} \\ \\ 35 &=\text{(50)(x)} \\ \\ 0.7 &=\text{x}\end{align*}[/latex] - 1.5 mL
[latex]\begin{align*} \dfrac{6}{x} &=\dfrac{4}{1} \\ \\ 6 &=\text{(4)(x)} \\ \\ 1.5 &=\text{x}\end{align*}[/latex] - 1.3 mL
[latex]\begin{align*} \dfrac{1300}{x} &=\dfrac{1000}{1} \\ \\ 1300 &=\text{(1000)(x)} \\ \\ 1.3 &=\text{x}\end{align*}[/latex] - 1.9 mL
[latex]\begin{align*} \dfrac{76}{x} &=\dfrac{40}{1} \\ \\ 76 &=\text{(40)(x)} \\ \\ 1.9 &=\text{x}\end{align*}[/latex] - 1.1 mL
[latex]\begin{align*} \dfrac{2.2}{x} &=\dfrac{2}{1} \\ \\ 2.2 &=\text{(2)(x)} \\ \\ 2.2 &=\text{x}\end{align*}[/latex] - 0.45 mL
[latex]\begin{align*} \dfrac{13.5}{x} &=\dfrac{30}{1} \\ \\ 13.5 &=\text{(30)(x)} \\ \\ 0.45 &=\text{x}\end{align*}[/latex] - 4 mL
[latex]\begin{align*} \dfrac{40}{x} &=\dfrac{10}{1} \\ \\ 40 &=\text{(10)(x)} \\ \\ 4 &=\text{x}\end{align*}[/latex]

