Foundational Math Skills

3 Fractions

Lesson

Learning Outcomes

By the end of this chapter, learners will be able to:

  • define fraction, improper fraction and mixed fraction,
  • simplify fractions,
  • add and subtract fractions, and
  • multiply and divide fractions.

Defining Fractions

Fractions

Fractions are useful when describing information which relates to parts of a whole. A fraction is a way of documenting the amount of parts present out of the total number of parts of a thing. They are also used when writing ratios and proportion equations, using algebra and determining percentages.

Fractions always have a minimum of two parts, a numerator and a denominator:

[latex]\dfrac{\text{numerator}}{\text{denominator}}[/latex]

Sometimes, a whole number may precede a fraction. We see this often in baking recipes. For instance, you might see a recipe require [latex]1\tfrac{1}{4}[/latex] cups of sugar.

Consider a package of a dozen assorted doughnuts. If 3 of the 12 doughnuts were raisin bran, the fraction would read as follows:

[latex]\dfrac{3}{12}[/latex]

The numerator is the portion present and the denominator are the number of parts in the whole (12 parts in a dozen).

Sample Exercise 3.1

How would you write a fraction if a pizza, with a total of 10 slices, had 5 slices with pineapple added on?

Answer:

[latex]\dfrac{5}{10}[/latex]

Fraction Types



[latex]\begin{array}{llll}\text{Fractions}&\hspace{1em}\dfrac{7}{8}&\hspace{1em}\dfrac{2}{15}&\hspace{1em}\dfrac{1}{3}\\\text{Improper fractions}&\hspace{1em}\dfrac{9}{8}&\hspace{1em}\dfrac{6}{3}&\hspace{1em}\dfrac{12}{5}\\\text{Mixed fractions}&\hspace{1em}2\dfrac{3}{4}&\hspace{1em}4\dfrac{5}{8}&\hspace{1em}1\dfrac{2}{5}\end{array}[/latex]




Improper Fractions


Improper fractions are simply fractions which have a larger numerator than denominator. If you think about a proper fraction as representing a portion of a whole, an improper fraction would be representing a value greater than one. It represents more pieces than are available in one whole item.


For instance, we could use an improper fraction to describe the total number of pizza slices. The image below represents three personal pizzas, each cut into four pieces. There is one piece missing from the last pizza. The fraction to describe this situation is:


[latex]\dfrac{11}{4}[/latex]




Mixed Fractions


Mixed fractions also represent a value that is greater than one whole. Instead of the numerator being larger than the denominator, the fraction is written with the amount of whole portions before the fraction. If you look at the pizza picture above, there are 2 whole pizzas plus 3 pieces left out of the four pieces which make up a whole pizza. Written as a fraction it looks like this:


[latex]2\dfrac{3}{4}[/latex]


Converting Improper Fractions to Mixed Fractions


In order to write an improper fraction as a mixed fraction, we need to know how many whole units there are. You can determine how many whole units there are by dividing the numerator by the denominator. Long division works well for this process, as the remainder becomes the numerator and the quotient becomes the whole number to the left of the fraction. Let’s start by looking at the improper fraction [latex]\tfrac{11}{4}[/latex] from the example above.


Long division terms: dividend divided by the divisor equals quotient with the remainder.


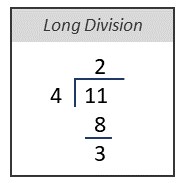
11 divided by 4 equals 2 with the remainder of 3.


Now to write as a mixed fraction the quotient (2) is the whole number written to the left of the fraction. The remainder (3) is the numerator and the divisor (4) is the denominator.


[latex]2\dfrac{3}{4}[/latex]






Sample Exercise 3.2






Convert [latex]\tfrac{15}{4}[/latex] into a mixed fraction.



Answer:

[latex]3\dfrac{3}{4}[/latex]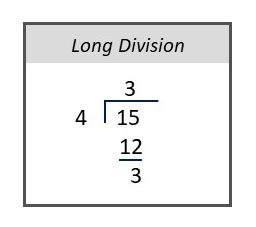15 divided by 4 equals 3 with the remainder of 3












Sample Exercise 3.3






Convert [latex]\tfrac{17}{4}[/latex] to a mixed fraction.



Answer: 

Using long division:


[latex]4\dfrac{1}{4}[/latex]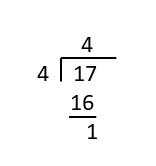Sample of long division, seventeen divided by four equals 4 with the remainder of 1


Alternately:


First, divide the numerator by the denominator to find out how many whole units there are.


[latex]17\div4 = 4.25[/latex]


The denominator stays the same.


The numerator is the portion of the whole: 0.25, or [latex]\tfrac{1}{4}[/latex].


[latex]4\dfrac{1}{4}[/latex]








Converting Mixed Fractions to Improper Fractions


When converting a mixed fraction to an improper fraction, the denominator always stays the same, as the number of parts in a whole item is not changing. To determine the numerator, you first multiply the whole number and denominator from the mixed fraction. This step determines how many pieces are in the number of whole items. Then add number of pieces represented by the numerator of the mixed fraction to this am


ount to calculate the total number of pieces. This number is now the new numerator of the improper fraction.


    

  • [latex]2\dfrac{3}{4}[/latex]
    • 

  • [latex]2\times4=8[/latex]
    • 

  • [latex]8+3=11[/latex]
    • 

  • [latex]\dfrac{11}{4}[/latex]
    • 







Sample Exercise 3.4






Convert [latex]3\tfrac{7}{8}[/latex] to an improper fraction.



Answer:

The denominator stays the same. 8.


To find the numerator, first multiply the whole number and denominator:


[latex]3\times8 = 24[/latex]


Add this number to the current numerator:


[latex]24+7 = 31[/latex]


Write the improper fraction:


[latex]\dfrac{31}{8}[/latex]








Simplifying Fractions


It is common practice to write fractions using the smallest numbers possible, as it is easier to conceptualize what the fraction represents when the numbers are small. This is also called reducing fractions. When we simplify a fraction, it does not change the size of the portion we are referring to because the relationship between the numerator and denominator does not change. For instance, try to picture [latex]\tfrac{2}{4}[/latex] of an orange. Now try to picture [latex]\tfrac{1}{2}[/latex] of an orange. They still refer to the same amount of the orange, even though the numbers of the fractions are different.


To simplify a fraction, you must divide the numerator and the denominator by the same number. If you are able to find the largest number you can divide both the numerator and denominator by, the fraction will be in simplified (or reduced) form. These numbers are also called the largest common factor.


As long as you divide by the same number, you do not change the relationship between the numerator and denominator. Fractions with small numbers, like [latex]\tfrac{2}{4}[/latex], can often be simplified with just one step, as it is easier to identify the largest common factor.


Fractions with larger numbers, like [latex]\tfrac{362}{900}[/latex] may take you a couple of steps, depending on your knowledge related to topics like multiplication tables and prime numbers Prime numbers have only two common factors, 1 and the number itself. If you spot a prime number in a fraction, you cannot simplify it any further. To reduce large numbers you cannot identify the largest common factor of, try dividing by 2 if they are both even numbers, by 5 if they end in a 5, or by 10 if they end in zeros.




[latex]\dfrac{362}{900}[/latex]


In this case, it’s not clear what the largest common factor is. Since they are both even, they can be divided by 2.


[latex]\dfrac{362\div2}{900\div2}[/latex]


[latex]\dfrac{181}{450}[/latex]


181 is a prime number, so this fraction is now reduced.








Sample Exercise 3.5






Simplify the following fraction:


[latex]\dfrac{440}{1200}[/latex]



Answer:

 [latex]\dfrac{440\div10}{1200\div10}=\dfrac{44}{120}[/latex]


[latex]\dfrac{44\div4}{120\div4}=\dfrac{11}{30}[/latex]


11 is a prime number, so now this fraction is reduced.








Adding and Subtracting Fractions


To add and subtract fractions, fractions must share the same denominator. When the denominators are the same, you can simply add or subtract the numerators as indicated in the math problem. Simplify the new fraction if possible.




Sample Addition of Fractions


[latex]\dfrac{1}{3}+\dfrac{3}{5}[/latex]


First, convert fractions as needed so they end up with the same denominator. In this case, we can make the common denominator 15.


[latex]\dfrac{1}{3}\times\dfrac{5}{5}=\dfrac{5}{15}[/latex]


[latex]\dfrac{3}{5}\times\dfrac{3}{3}=\dfrac{9}{15}[/latex]


Second, add the numerators.


[latex]\dfrac{5}{15}+\dfrac{9}{15}=\dfrac{14}{15}[/latex]


Third, simplify if possible.


[latex]\tfrac{14}{15}[/latex] is in the simplest form.








Sample Exercise 3.6






[latex]\dfrac{8}{12}-\dfrac{1}{6}[/latex]



Answers:

 


Find common denominator and convert fractions, subtract second numerator, simplify.


[latex]\dfrac{8}{12}-\left(\dfrac{1}{6}\times\dfrac{2}{2}\right)[/latex]


[latex]\dfrac{8}{12}-\dfrac{2}{12}=\dfrac{6}{12}[/latex]


[latex]\dfrac{6\div6}{12\div6}=\dfrac{1}{2}[/latex]








Multiplying Fractions


To multiply fractions, all you need to do is multiply the numerators together and then multiply the denominators together to determine the numerator and denominator of the new fraction. You will need to convert any mixed fractions to improper fractions before multiplying the numerators together. Simplify your answer as needed.




Sample Multiplication of Fractions


[latex]\dfrac{5}{7}\times\dfrac{2}{6}[/latex]


First, check to see if there are mixed fractions which need to be converted to improper fractions. In this question, there is not.


Second, multiply the numerators and then the denominators.


[latex]\dfrac{5\times2}{7\times6} = \dfrac{10}{42}[/latex]


Third, simplify.


[latex]\dfrac{10\div2}{42\div2} = \dfrac{5}{21}[/latex]








Sample Exercise 3.7






[latex]\dfrac{3}{4}\times1\dfrac{1}{2}[/latex]



Answer:

Convert to an improper fraction:


[latex]\dfrac{3}{4}\times\dfrac{3}{2}[/latex]


Multiply numerators then denominators:


[latex]\dfrac{3\times3}{4\times2} = \dfrac{9}{8}[/latex]


Simplify:


[latex]1\dfrac{1}{8}[/latex]








Dividing Fractions


To divide fractions, start by converting any mixed fractions to improper fractions. To divide a fraction, you will actually multiply the first fraction by the reciprocal of the second. To create the reciprocal of a fraction, all you need to do is switch the places of the numerator and denominator.


Reciprocal Fractions


[latex]\dfrac{2}{3}[/latex] = [latex]\dfrac{3}{2}[/latex]




Sample Division of Fractions


[latex]1\dfrac{7}{8}\div\dfrac{2}{3}[/latex]


First, convert any mixed fractions to improper fractions.


[latex]\dfrac{15}{8}\div\dfrac{2}{3}[/latex]


Second, invert the second fraction to its reciprocal and change your symbol.


[latex]\dfrac{15}{8}\times\dfrac{3}{2}[/latex]


Third, multiply across.


[latex]\dfrac{15}{8}\times\dfrac{3}{2} = \dfrac{45}{16}[/latex]


Simplify.


[latex]\dfrac{45}{16} = 2\dfrac{13}{16}[/latex]










Sample Exercise 3.8






[latex]\dfrac{3}{12}\div\dfrac{2}{3}[/latex]



Answer:

Multiply the first fraction by the reciprocal of the second.


[latex]\dfrac{3}{12}\times\dfrac{3}{2} = \dfrac{9}{24}[/latex]


Divide the numerator and denominator by 3 to simplify.


[latex]\dfrac{3}{8}[/latex]












Key Takeaways






    

  • Fractions are comprised of a numerator and denominator.
    • 

  • Mixed fractions have a whole number to the left of the fraction.
    • 

  • Improper fractions have a numerator larger than the denominator.
    • 

  • To simplify fractions, divide the numerator and the denominator by the largest common factor.
    • 

  • To add and subtract fractions, add or subtract the numerators of fractions with the same denominator.
    • 

  • To multiply fractions, multiply the numerators and then multiply the denominators.
    • 

  • To divide fractions, multiply the first fraction by the reciprocal of the second.
    • 

  • Always simplify fractions when able.
    • 







Practice Set 3.1: Simplifying Fractions






Practice Set 3.1: Simplifying Fractions






Simplify the following fractions. Click the word Answers to check your work.


    

  1. [latex]\dfrac{6}{16}[/latex]
    2. 

  2. [latex]\dfrac{3}{9}[/latex]
    3. 

  3. [latex]\dfrac{10}{25}[/latex]
    4. 

  4. [latex]\dfrac{32}{56}[/latex]
    5. 

  5. [latex]\dfrac{22}{44}[/latex]
    6. 

  6. [latex]\dfrac{14}{21}[/latex]
    7. 

  7. [latex]\dfrac{13}{13}[/latex]
    8. 

  8. [latex]\dfrac{30}{24}[/latex]
    9. 

  9. [latex]\dfrac{66}{14}[/latex]
    10. 

  10. [latex]\dfrac{70}{15}[/latex]
    11. 




Answers:

    

  1. [latex]\dfrac{6\div2}{16\div2}=\dfrac{3}{8}[/latex]
    2. 

  2. [latex]\dfrac{3\div3}{9\div3}=\dfrac{1}{3}[/latex]
    3. 

  3. [latex]\dfrac{10\div5}{25\div5}=\dfrac{2}{5}[/latex]
    4. 

  4. [latex]\dfrac{32\div8}{56\div8}=\dfrac{4}{7}[/latex]
    5. 

  5. [latex]\dfrac{22\div22}{44\div22}=\dfrac{1}{2}[/latex]
    6. 

  6. [latex]\dfrac{14\div7}{21\div7}=\dfrac{2}{3}[/latex]
    7. 

  7. [latex]\dfrac{13\div13}{13\div13}=\dfrac{1}{1}=1[/latex]
    8. 

  8. [latex]\dfrac{30\div6}{24\div6}=\dfrac{5}{4}=1\dfrac{1}{4}[/latex]
    9. 

  9. [latex]\dfrac{66\div2}{14\div2}=\dfrac{33}{7}=4\dfrac{5}{7}[/latex]
    10. 

  10. [latex]\dfrac{70\div5}{15\div5}=\dfrac{14}{3}=4\dfrac{2}{3}[/latex]
    11. 









Practice Set 3.2: Adding and Subtracting Fractions






Practice Set 3.2: Adding and Subtracting Fractions






Add or subtract the following fractions. Click the word Answers to check your work.


    

  1. [latex]\dfrac{1}{3}+\dfrac{1}{3}[/latex]
    2. 

  2. [latex]\dfrac{9}{10}-\dfrac{1}{5}[/latex]
    3. 

  3. [latex]\dfrac{1}{4}+\dfrac{2}{3}[/latex]
    4. 

  4. [latex]\dfrac{3}{4}-\dfrac{1}{7}[/latex]
    5. 

  5. [latex]\dfrac{1}{2}+\dfrac{1}{4}[/latex]
    6. 

  6. [latex]\dfrac{2}{3}-\dfrac{1}{9}[/latex]
    7. 

  7. [latex]\dfrac{2}{5}+\dfrac{1}{6}[/latex]
    8. 

  8. [latex]\dfrac{2}{3}+\dfrac{5}{6}[/latex]
    9. 

  9. [latex]\dfrac{7}{8}-\dfrac{1}{2}[/latex]
    10. 

  10. [latex]\dfrac{5}{6}-\dfrac{1}{10}[/latex]
    11. 




Answers:

    

  1. [latex]\dfrac{2}{3}[/latex]
    2. 

  2. [latex]\dfrac{9}{10}-\left(\dfrac{1}{5}\times\dfrac{2}{2}\right) = \dfrac{9}{10}-\dfrac{2}{10}=\dfrac{7}{10}[/latex]
    3. 

  3. [latex]\left(\dfrac{1}{4}\times\dfrac{3}{3}\right)+\left(\dfrac{2}{3}\times\dfrac{4}{4}\right) = \dfrac{3}{12}+\dfrac{8}{12} = \dfrac{11}{12}[/latex]
    4. 

  4. [latex]\left(\dfrac{3}{4}\times\dfrac{7}{7}\right)-\left(\dfrac{1}{7}\times\dfrac{4}{4}\right) = \dfrac{21}{28}-\dfrac{4}{28} = \dfrac{17}{28}[/latex]
    5. 

  5. [latex]\left(\dfrac{1}{2}\times\dfrac{2}{2}\right)+\dfrac{1}{4} = \dfrac{2}{4}+\dfrac{1}{4} = \dfrac{3}{4}[/latex]
    6. 

  6. [latex]\left(\dfrac{2}{3}\times\dfrac{3}{3}\right)-\dfrac{1}{9} = \dfrac{6}{9}-\dfrac{1}{9} = \dfrac{5}{9}[/latex]
    7. 

  7. [latex]\left(\dfrac{2}{5}\times\dfrac{6}{6}\right)+\left(\dfrac{1}{6}\times\dfrac{5}{5}\right) = \dfrac{12}{30}+\dfrac{5}{30} = \dfrac{17}{30}[/latex]
    8. 

  8. [latex]\left(\dfrac{2}{3}\times\dfrac{2}{2}\right)+\dfrac{5}{6} = \dfrac{4}{6}+\dfrac{5}{6} = \dfrac{9}{6} = 1\dfrac{3}{6} = 1\dfrac{1}{2}[/latex]
    9. 

  9. [latex]\dfrac{7}{8}-\left(\dfrac{1}{2}\times\dfrac{4}{4}\right) = \dfrac{7}{8}-\dfrac{4}{8}=\dfrac{3}{8}[/latex]
    10. 

  10. [latex]\left(\dfrac{5}{6}\times\dfrac{5}{5}\right)-\left(\dfrac{1}{10}\times\dfrac{3}{3}\right) = \dfrac{25}{30}-\dfrac{3}{30}=\dfrac{22}{30} = \dfrac{22\div2}{30\div2} = \dfrac{11}{15}[/latex]
    11. 









Practice Set 3.3: Multiplying and Dividing Fractions






Practice Set 3.3: Multiplying and Dividing Fractions






Multiply or divide the following. Be sure to simplify all answers and write them as a mixed fraction when possible. Click on the word Answers to check your work.


    

  1. [latex]\dfrac{7}{10}\times\dfrac{1}{5}[/latex]
    2. 

  2. [latex]\dfrac{2}{4}\times\dfrac{1}{2}[/latex]
    3. 

  3. [latex]\dfrac{3}{7}\times\dfrac{5}{12}[/latex]
    4. 

  4. [latex]3\dfrac{2}{3}\times\dfrac{7}{8}[/latex]
    5. 

  5. [latex]1\dfrac{3}{5}\times4\dfrac{5}{6}[/latex]
    6. 

  6. [latex]\dfrac{4}{9}\div\dfrac{1}{2}[/latex]
    7. 

  7. [latex]\dfrac{2}{3}\div\dfrac{6}{10}[/latex]
    8. 

  8. [latex]\dfrac{3}{5}\div\dfrac{4}{7}[/latex]
    9. 

  9. [latex]\dfrac{6}{13}\div\dfrac{4}{5}[/latex]
    10. 

  10. [latex]\dfrac{1}{4}\div\dfrac{3}{9}[/latex]
    11. 




Answers:

    

  1. [latex]\dfrac{7}{50}[/latex]
    2. 

  2. [latex]\dfrac{2}{8} = \dfrac{1}{4}[/latex]
    3. 

  3. [latex]\dfrac{3}{7}\times\dfrac{5}{12} = \dfrac{15}{84}= \dfrac{5}{28}[/latex]
    4. 

  4. [latex]\dfrac{11}{3}\times\dfrac{7}{8} = \dfrac{77}{24} = 3\dfrac{5}{24}[/latex]
    5. 

  5. [latex]\dfrac{8}{5}\times\dfrac{29}{6}= \dfrac{232}{30} = 7\dfrac{22}{30} = 7\dfrac{11}{15}[/latex]
    6. 

  6. [latex]\dfrac{4}{9}\times\dfrac{2}{1} = \dfrac{8}{9}[/latex]
    7. 

  7. [latex]\dfrac{2}{3}\times\dfrac{10}{6} = \dfrac{20}{18} = 1\dfrac{2}{18} = 1\dfrac{1}{9}[/latex]
    8. 

  8. [latex]\dfrac{3}{5}\times\dfrac{7}{4} = \dfrac{21}{20} = 1\dfrac{1}{20}[/latex]
    9. 

  9. [latex]\dfrac{6}{13}\times\dfrac{5}{4} = \dfrac{30}{52}= \dfrac{15}{26}[/latex]
    10. 

  10. [latex]\dfrac{1}{4}\times\dfrac{9}{3} = \dfrac{9}{12}= \dfrac{3}{4}[/latex]
    11. 









definition





					
		
					

						

							
							

								
License

								
Icon for the Creative Commons Attribution 4.0 International License
A Guide to Numeracy in Nursing Copyright © 2023 by Julia Langham is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.
							

														

								
Share This Book