Math for Medication Administration
16 IV Flow Rates
Lesson
Learning Outcomes
By the end of this chapter, learners will be able to:
- define the terms rate, drop factor, and drop rate,
- distinguish between micro and macro drip tubing,
- calculate infusion rate,
- calculate drop rate, and
- calculate infusion time.
When administering intravenous (IV) fluids, you will come across a variety of ways prescribers write IV orders. You will need to be familiar with the types of information presented in the order, how to use this information correctly when administering IV fluid and how to make this information meaningful when discussing the IV treatment with the client. Much of this information is related to the amount of fluid they will receive, either the total amount or the amount infused each hour. The type of equipment you have available will impact how the IV infusion is set up, so it is important to understand how the equipment works and how it can impact how fluid is infused.
Calculating the IV Infusion Rate
The term rate refers to an amount over a period of time. When we consider intravenous (IV) fluid treatments, the rate is typically measured in millilitres/hour (mL/hr). Most of the time, IV pumps will be set to infuse IV fluids in mL/hr as well, but there are some exceptions when we are infusing IV medications. Just like other med math questions, you need to make sure you are always considering the type of units written in the order and what you have available in your supply when preparing medications as you may need to convert units before completing your calculation.
You can use the formula above to help you quickly calculate a rate if the rate is not specifically written in the order. You can also use dimensional analysis to calculate rate when unit conversion is necessary.
Sample Exercise 16.1
IV infusion order: Run 500 mL of normal saline over 4 hours. What rate would this IV run at?
Answer:
[latex]\text{rate}=\dfrac{\text{total volume}}{\text{time in hours}}[/latex]
[latex]\text{rate}=\dfrac{\text{500 mL}}{\text{4 hours}}[/latex]
[latex]\text{rate}=\text{125 mL/hr}[/latex]
Sample Exercise 16.2
IV infusion order: Run 1 L of D5W over 4 hours. What rate would this IV run at?
Answer:
[latex]\text{rate}=\dfrac{\text{total volume}}{\text{time in hours}}[/latex]
[latex]\dfrac{\text{mL}}{\text{hr}}=\dfrac{\text{1000 mL}}{\text{1 L}}\times\dfrac{\text{1 L}}{\text{4 hours}}[/latex]
[latex]\dfrac{\text{mL}}{\text{hr}}=\dfrac{\text{1000 mL}}{1\cancel{\text{ L}}}\times\dfrac{1\cancel{\text{ L}}}{\text{4 hours}}[/latex]
[latex]\dfrac{\text{mL}}{\text{hr}}=\text{250 mL/hr}[/latex]
Calculating the IV Drop Rate
When you watch an IV infuse, you can see drops falling from where the IV tubing enters the drop chamber. The drop rate refers to how fast the IV fluid is dripping, measured in drops/minute (gtts/min). When there is no pump available, you must set the rate manually by using the roller clamp to control the flow and watching how quickly the drops are dripping in the drip chamber. In order to determine exactly how fast we should let the IV drip, we need to consider how big each drop is, and count how many drops are falling in a minute. Each IV set you use has a specific size drop it produces, some large, others small. The size of drop is reflected in the drop factor which is identified on the IV set packaging. The drop factor tells you how many drops are in 1 mL of fluid, which you can use to help calculate the rate the IV should run. In the image below, you can see the size difference between a large drop of a macro set and a small drop of a micro set.
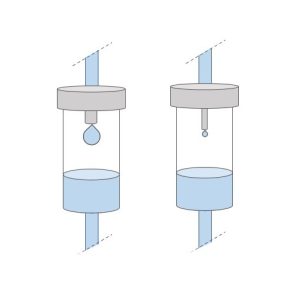
Note the drop rate is measured in gtts/min, versus the infusion rate which is measured in mL/hr. To calculate the drop rate you must know the infusion rate and the drop factor of the IV tubing. You can use the formula below, but only if you convert the rate of mL/hr to mL/min. As IV rates are usually given in mL/1 hr, you should be able to use 60 minutes as the denominator in most cases.
You can see how this works using dimensional analysis:
Consider an IV running at 125mL/hr, using a standard tubing set with a drop factor of 10 gtts/mL. What is the drop rate in gtts/min?
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{10\text{ gtts}}{1\text{ mL}}\times\dfrac{125\text{ mL}}{1\text{ hr}}\times \dfrac{1\text{hr}}{60\text{ min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{10\text{ gtts}}{1\cancel{\text{ mL}}}\times\dfrac{125\cancel{\text{ mL}}}{1\cancel{\text{ hr}}}\times \dfrac{1\cancel{\text{hr}}}{60\text{ min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 125}}{\text{60 min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{1250 gtts}}{\text{60 min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \text{20.83}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \text{21}[/latex]
*round to the whole number as you cannot count a portion of a drop
Critical Thinking Questions
- If an IV set creates a large drop, will the patient finish the infusion more quickly than an IV set which creates a small drop?
- If the drop rate is calculated at 15.5, what do you set the drop rate at when administering the IV?
Answers:
- If the rate is set in mL/hr, then both infusions should finish at the same time. Macro drips will take less drops to fill 1 mL than a micro drip set, so if you compare the drops falling in the drop chamber, the drops per minute in the IV set with small drops will be running at a faster rate (drops/min). If we compare two infusions with the same drop rate, then the infusion running with the macro set would finish faster as more volume per drop is being infused, however IV infusions are not ordered with a drop/minute rate because of this variability.
- Drops must be rounded up or down, as you cannot count a portion of a drop. So do you choose 15 or 16? The actual difference of fluid administered in one hour between a drop rate of 15 and 16 is only 6 mL. When the IV infusion is running by gravity, there are fluctuations in the actual rate of the IV infusion and you will need to keep readjusting the drop rate to keep the IV running at the appropriate rate. So, it is likely that you can choose either drop rate, knowing that you will be frequently readjusting the drop rate to ensure the fluid infuses in the correct amount of time. However, if the extra 6 mL/hour of fluid would be detrimental to your client, then you should find a pump and ensure a more exact rate is delivered to the client. Instances where the infusion is a medication or the client is at risk for fluid overload may be circumstances which require the pump versus gravity.
Sample Exercise 16.3
Calculate the drop rate for the following order:
Give NS IV 70 mL/hr.
The IV set has a drop factor of 10 gtts/min.
Answer:
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{10\text{ gtts}}{1\text{ mL}}\times\dfrac{70\text{ mL}}{1\text{ hr}}\times \dfrac{1\text{hr}}{60\text{ min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 70}}{\text{60 min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{700 gtts}}{\text{60 min}}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= \text{11.66}[/latex]
[latex]\dfrac{\text{gtts}}{\text{min}}= 12[/latex]
Calculating IV Infusion Time
In some cases, you may want to know how long an IV infusion is going to take. Perhaps you need to know how long the IV will take to infuse in order to inform the patient how long it will be until they take a shower, or to be discharged home. Most IV pumps will display the remaining time of the infusion, but you may need this information before you have programmed infusion details into the IV pump. Understanding how to calculate infusion time can help you be prepared to plan timing of infusions and answer questions about the infusion time promptly.
Sample Exercise 16.4
A client has the following order: Infuse 1 L NS at 125 mL/hr.
How long will this take to infuse?
Answer:
[latex]\text{infusion time}=\dfrac{\text{total volume}}{\text{rate}}[/latex]
[latex]\text{infusion time}=\dfrac{\text{1000}}{\text{125}}[/latex]
[latex]\text{infusion time}=8[/latex]
Here is the same question showing how dimensional analysis is used, and where the units will cancel out:
[latex]\text{infusion time}=\dfrac{\text{1 hr}}{\text{125 mL}}\times\text{1000 mL}[/latex]
[latex]\text{infusion time}=\dfrac{\text{1 hr}}{125\cancel{\text{ mL}}}\times1000\cancel{\text{ mL}}[/latex]
[latex]\text{infusion time}=\text{8 hrs}[/latex]
Critical Thinking Questions
A patient asks you how much longer their IV will run for. You manually calculate the remaining amount of time and determine the answer is 1.66 hours. How could you communicate this information to the client in a way that is easier to understand?
Answer:
You could report the remaining amount of time in hours and minutes. First, convert 0.66 into minutes (39.6 mins) and then inform the patient the infusion will run for about 1 hour and 40 minutes.
You could inform the client what time the infusion will finish. For instance, if it was 0800 hours, you could report the infusion will be finished around 0940 hours if the infusion is uninterrupted.
Key Takeaways
- Infusion rate is measured in mL/hr.
- Drop rate is measured in gtts/hr.
- Micro drip tubing has a drop factor of 60 gtts/mL.
- Standard tubing has a drop factor of 10 gtts/mL.
- Drop rate = Infusion Time x Drop Factor
Practice Set 16.1-16.3: Calculating IV Flow Rate
Practice Set 16.1: Calculating IV Flow Rate
Calculate the IV flow rate for the following IV infusion orders:
- Run 500 mL of normal saline over 2 hours.
- Give 1 L of Ringer’s lactate over 12 hours.
- Run 1 L of normal saline over 4 hours.
- Administer 1 L bolus of NS over 2 hours.
- Give 250 ml of 3% sodium chloride over 30 minutes.
- Run 1 L D5 0.45% NS over 5 hours.
- Infuse 500 mL D10W over 4 hours.
- Give 1,000 mL of D5W over 8 hours.
- Administer 750 mL of Ringer’s lactate over 8 hours.
- Give a 500 mL bolus of NS over an hour and a half.
Answers:
Answers should be in mL/hr. Use dimensional analysis or the formula [latex]\text{rate}=\dfrac{\text{total volume}}{\text{total time}}[/latex].
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{2 hours}}=\text{250 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{12 hours}}=\text{83 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{4 hours}}=\text{250 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{2 hours}}=\text{500 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{250 mL}}{\text{30 minutes}}=\dfrac{\text{250 mL}}{\text{0.5 hours}}=\text{500 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{5 hours}}=\text{200 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{4 hours}}=\text{125 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{8 hours}}=\text{125 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{750 mL}}{\text{8 hours}}=\text{94 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{1.5 hours}}=\text{333 mL/hr}[/latex]
Practice Set 16.2: Calculating IV Flow Rates
Calculate the IV flow rate for the following IV infusion orders:
- Give 600 mL over 120 minutes.
- Administer 1 L of NS over 8 hours.
- Run 750 mL over 4 hours.
- Run 500 mL over 210 minutes.
- Give a 1 L Ringer’s Lactate bolus over 90 minutes.
- Administer 800 mL over 6 hours.
- Administer 500 mL over 2 hours.
- Run 800 mL NS over 4 hours.
- Give a 250 mL bolus over 30 minutes.
- Run 500 mL over 6 hours.
Answers:
- [latex]\text{rate}=\dfrac{\text{600 mL}}{\text{120 minutes}}=\dfrac{\text{600 mL}}{\text{2 hours}}=\text{300 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{8 hours}}=\text{125 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{750 mL}}{\text{4 hours}}=\text{187.5 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{210 minutes}}=\dfrac{\text{500 mL}}{\text{3.5 hours}}=\text{143 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{90 minutes}}=\dfrac{\text{1000}}{\text{1.5 hours}}=\text{666 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{800 mL}}{\text{6 hours}}=\text{133 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{2 hours}}=\text{250 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{800 mL}}{\text{4 hours}}=\text{200 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{250 mL}}{\text{30 minutes}}=\dfrac{\text{250}}{\text{0.5 hours}}=\text{500 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{6 hours}}=\text{83 mL/hr}[/latex]
Practice Set 16.3: Calculating Infusion Rate
Calculate the infusion rate for the following IV orders:
- You need to administer 10,800 mL of Ringer’s lactate over 24 hours to a patient with burns to 45% of their total body surface area. How many mL/hour will you program on the IV pump and how many 1 L bags of Ringer’s lactate will you go through in the first 24 hours?
- A person arrives to the emergency room in hemorrhagic shock. The physician prescribes 1 unit of packed red blood cells (PRBC) to be given over 20 minutes and the unit you collect from blood services has 346 mL of PRBC. What would you program as the infusion rate on the pump?
- A person is severely hypokalemic but is NPO and cannot take oral potassium. Your order is to give 40 mEq of potassium in 1L lactated Ringer’s over 4 hours. What would your infusion rate be?
- You are working on the surgical floor and one of your patients is having severe postoperative nausea after hip replacement surgery. The physician has ordered 4 mg of ondansetron to help with this nausea. Using the parenteral manual you have decided to dilute the medication in a 50 mL minibag and give over 15 minutes because your patient is over 65 years old but has been tolerating fluids well. What will your infusion rate be?
- You have a patient on the medical floor who is having an allergic reaction to one of the medications that the doctor has ordered. The doctor has now ordered 50 mg diphenhydramine which you have diluted in a 50 mL minibag that you are going to run over 20 minutes. What will your infusion rate be?
- A patient comes into the emergency room with the flu severely dehydrated and unable to tolerate fluids by mouth. The physician orders 1 L of Ringer’s lactate over four and a half hours. What will your infusion rate be?
- You have a child who came into the hospital in ventricular fibrillation. The doctor has ordered 160 mg of amiodarone which you have diluted in a 50 mL minibag of D5W and you choose to give this dose over 30 minutes. What will your infusion rate be?
- A woman who is 26 weeks pregnant was admitted for hyperemesis gravidarum treatment. The midwife has ordered 100 mg diphenhydrinate IV. You have diluted this in 1 L of D5W and are going to give over 10 hours. What will your infusion rate be?
- You are receiving a postoperative patient from the PAR who is on a ketorolac infusion that is almost complete. The surgeon wants another 10 mg hung and you add the medication into a 50 mL bag to run over 30 minutes. What will your infusion rate be?
- Your patient has been NPO for a couple of days as their surgery has been postponed. In the meantime, the physician has ordered 1 L over 4 hours. What will the infusion rate be?
Answers:
- [latex]\text{rate}=\dfrac{\text{10800 mL}}{\text{24 hours}}=\text{450 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{346 mL}}{\text{20 minutes}}=\dfrac{\text{346 mL}}{\text{0.33 hours}}=\text{1048 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{4 hours}}=\text{250 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{50 mL}}{\text{15 minutes}}=\dfrac{\text{50 mL}}{\text{0.25 hours}}=\text{200 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{50 mL}}{\text{20 minutes}}=\dfrac{\text{50 mL}}{\text{0.33 hours}}=\text{151 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{4.5 hours}}=\text{222.2 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{50 mL}}{\text{30 minutes}}=\dfrac{\text{50 mL}}{\text{0.5 hours}}=\text{100 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{10 hours}}=\text{100 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{50 mL}}{\text{30 minutes}}=\dfrac{\text{50 mL}}{\text{0.5 hours}}=\text{100 mL/hr}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{4 hours}}=\text{250 mL/hr}[/latex]
Practice Set 16.4-16.6: Calculating IV Drop Rate
Practice Set 16.4: Calculating IV Drop Rate
Calculate the drop rate for the following IV orders:
- IV NS 125 ml/hr using standard tubing
- IV D5W 80 ml/hr using standard tubing
- IV RL 150 ml/hr using standard tubing
- IV NS 25 ml/hr using microdrip tubing
- IV RL 35 ml/hr using microdrip tubing
- IV 0.45% NS 100 ml/hr using standard tubing
- IV NS 130 ml/hr using standard tubing
- IV D5W 15 ml/hr using microdrip tubing
- IV NS 55 ml/hr using standard tubing
- IV NS 200 ml/hr using standard tubing
Answers:
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 125}}{\text{60 min}}=\text{21}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 80}}{\text{60 min}}=13[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 150}}{\text{60 min}}=\text{25}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{60 gtts x 25}}{\text{60 min}}=\text{25}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{60 gtts x 35}}{\text{60 min}}=\text{35}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 100}}{\text{60 min}}=17[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 130}}{\text{60 min}}=\text{22}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{60 gtts x 15}}{\text{60 min}}=15[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 55}}{\text{60 min}}=9[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 200}}{\text{60 min}}=\text{33}[/latex]
Practice Set 16.5: Calculating IV Drop Rate
Calculate the drop rate for the following IV orders:
- Run 1L NS over 4 hours, standard tubing
- IV RL 70 ml/hr, macro drip tubing 20 gtts/min
- IV NS 25 ml/hr, micro drip tubing
- IV D5W 175 ml/hr, standard tubing
- IV RL 76 ml/hr, standard tubing
- Infuse 500 ml NS over 2 hours, standard tubing
- IV NS 135 ml/hr, standard tubing
- Give 1L RL over 8 hours, standard tubing
- IV NS 40 ml/hr, macro drip tubing 15 gtts/min
- IV D5W 60ml/hr, standard tubing
Answers:
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{4 hours}}=\text{250 mL/hr}=\dfrac{\text{10 gtts x 250}}{\text{60 min}}=\text{42}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{20 gtts x 70}}{\text{60 min}}=\text{23}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{60 gtts x 25}}{\text{60 min}}=\text{25}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 175}}{\text{60 min}}=\text{29}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 75}}{\text{60 min}}=12[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{2 hours}}=\text{250 mL/hr}=\dfrac{\text{10 gtts x 250}}{\text{60 min}}=\text{42}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 135}}{\text{60 min}}=\text{22}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{8 hours}}=\text{125 mL/hr}=\dfrac{\text{10 gtts x 125}}{\text{60 min}}=\text{21}[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{15 gtts x 40}}{\text{60 min}}=10[/latex]
- [latex]\dfrac{\text{gtts}}{\text{min}}= \dfrac{\text{10 gtts x 60}}{\text{60 min}}=10[/latex]
Practice Set 16.6: Calculating IV Drop Rate
Calculate the drop rate for the following IV orders:
- IV RL 50 mL/hr using standard tubing.
- IV NS 175 mL/hr using microdrip tubing.
- IV D5W 500 mL over 3 hours using microdrip tubing.
- IV RL 250 mL/hr using standard tubing.
- IV NS 1L over 6 hours using standard tubing.
- IV RL 75 mL/hr using standard tubing.
- IV D5W 250 mL over 3 hours using standard tubing.
- IV D5W 100 mL/hr using macrodrip tubing 20 gtts/min.
- IV NS 30 mL/hr using microdrip tubing.
- IV NS 50 mL over 30 minutes using macrodrip tubing 15 gtts/min.
Answers:
- [latex]\text{rate}=\text{50 mL/hr}=\dfrac{\text{10 gtts x 50}}{\text{60 min}}=\text{8.3}[/latex]
- [latex]\text{rate}=\text{175 mL/hr}=\dfrac{\text{60 gtts x 175}}{\text{60 min}}=\text{175}[/latex]
- [latex]\text{rate}=\dfrac{\text{500 mL}}{\text{3 hours}}=\text{166 mL/hr}=\dfrac{\text{60 gtts x 166}}{\text{60 min}}=\text{166}[/latex]
- [latex]\text{rate}=\text{250 mL/hr}=\dfrac{\text{10 gtts x 250}}{\text{60 min}}=\text{41.6}[/latex]
- [latex]\text{rate}=\dfrac{\text{1000 mL}}{\text{6 hours}}=\text{166.6 mL/hr}=\dfrac{\text{10 gtts x 166.6}}{\text{60 min}}=\text{27.2}[/latex]
- [latex]\text{rate}=\text{75 mL/hr}=\dfrac{\text{10 gtts x 75}}{\text{60 min}}=\text{12.5}[/latex]
- [latex]\text{rate}=\dfrac{\text{250 mL}}{\text{3 hours}}=\text{83.3 mL/hr}=\dfrac{\text{10 gtts x 83.3}}{\text{60 min}}=\text{13.8}[/latex]
- [latex]\text{rate}=\text{100 mL/hr}=\dfrac{\text{20 gtts x 100}}{\text{60 min}}=\text{33.3}[/latex]
- [latex]\text{rate}=\text{30 mL/hr}=\dfrac{\text{60 gtts x 30}}{\text{60 min}}=\text{30}[/latex]
- [latex]\text{rate}=\dfrac{\text{50 mL}}{\text{30 min}}=\text{100 mL/hr}=\dfrac{\text{15 gtts x 100}}{\text{60 min}}=\text{25}[/latex]
Practice Set 16.7-16.8: Calculating Infusion Time
Practice Set 16.7: Calculating Infusion Time
Calculate the infusion time for the following problems:
- A client has an IV infusing at 70 mL/hr. There is 140 mL left to be infused. How long will it take to infuse the rest of the fluid?
- A client has an IV infusing at 125 ml/hr. There is 587 mL left to be infused. How long will it take to infuse the rest of the fluid?
- A client has an IV infusing at 150 mL/hr. There is 225 mL left to be infused. How long will it take until the IV fluid has infused?
- A client has an IV infusing at 100 mL/hr. There is 850 mL left to be infused. How long will it take until the IV fluid has infused?
- A client has an IV infusing at 80 mL/hr. There is 320 mL left to be infused. How long will it take until the IV fluid has infused?
- A client has an IV infusing at 125 mL/hr. There is 725 mL left to be infused. How long will it take until the IV infusion is complete?
- A client has an IV infusing at 80 mL/hr. There is 409 mL left to be infused and it is currently 1945. What time should you expect to change the IV bag?
- A client has an IV infusing at 125 mL/hr. They can be discharged when the IV bag is empty. There is currently 340 mL of fluid remaining. How long will it be until they can be discharged?
- A client has an IV infusing at 100 mL/hr. There is 385 mL left to be infused and it is currently 0735. What time should you expect to change the IV bag?
- A client has an IV bolus running at 500 mL/hr, with 200 mL already infused. It is currently 1425. When the bolus is complete they will be taken for a CT scan. What time should you ask the porter to pick up the client?
Answers:
- [latex]\text{infusion time}=\dfrac{\text{140}}{\text{70}}=\text{2 hrs}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{587}}{\text{125}}=\text{4.696 hr}=\text{4 hr 42 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{225}}{\text{150}}=\text{1.5 hr}=\text{1 hr 30 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{850}}{\text{100}}=\text{8.5 hrs}=\text{8 hr 30 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{320}}{\text{80}}=\text{4 hrs}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{725}}{\text{125}}=\text{5.8 hrs}=\text{5 hr 48 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{409}}{\text{80}}=\text{5.1125 hrs}=\text{5 hr 7min}=\text{0052 hours}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{340}}{\text{125}}=\text{2.72 hrs}=\text{2 hr 43 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{385}}{\text{100}}=\text{3.85 hrs}=\text{3 h 51 min hrs}=\text{1126 hours}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{300}}{\text{500}}=\text{0.6 hrs}=\text{36 min}=\text{1501}=\text{1500 hours}[/latex]
*to easily convert a portion of an hour to minutes, multiply 60 by the portion of the hour.
2.35 hours converts to 2 hours and 21 minutes
[latex]0.35\times60=21[/latex]
Practice Set 16.8: Calculating Infusion Time
Calculate the infusion time for the following problems:
- A client has an IV infusing at 75 mL/hr. There is 346 mL left to be infused. How long until you will need to change the IV bag?
- A client has an IV infusing at 250 mL/hr. There is 115 mL left to be infused. The patient will be discharged when the infusion is finished, how long until the patient can be discharged?
- A client has an IV infusing at 33 mL/hr. There is 453 mL left to be infused. It is 0945, at what time should you change the IV bag next?
- A client has an IV infusing at 80 mL/hr. There is 235 mL left to be infused. How long until you change to the next IV bag?
- A client has an IV infusing at 125 mL/hr. There is 167 mL left to be infused. It is 1000, when can you change the IV bag next?
- A client has an IV infusing at 100 mL/hr. There is 245 mL left to be infused. It is 1635, when should the IV bag be changed next?
- A client has an IV infusing at 55 mL/hr. There is 374 mL left to be infused. It is 0745, the patient will be going to physio after their infusion is complete, when will physio expect them for?
- A client has an IV infusing at 500 mL/hr. There is 238 mL left to be infused. When the bolus is completed, the patient is to go to have an MRI, when should you tell the MRI staff to expect the patient?
- A client has an IV infusing at 200 mL/hr. There is 784 mL left to be infused. How long until you change the IV bag?
- A client has an IV infusing at 83 mL/hr. There is 675 mL left to be infused. Your patient can be discharged when the infusion finishes, how long until the patient can be discharged?
Answers:
- [latex]\text{infusion time}=\dfrac{\text{346}}{\text{75}}=\text{4.613 hrs}=\text{4 hr 37 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{115}}{\text{250}}=\text{0.46 hr}=\text{28 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{453}}{\text{33}}=\text{13.7 hr}=\text{13 hr 44 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{253}}{\text{80}}=\text{2.94 hrs}=\text{2 hr 56 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{167}}{\text{125}}=\text{1.336 hrs}=\text{1 hr 20 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{245}}{\text{100}}=\text{2.45 hrs}=\text{2 hr 27 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{374}}{\text{55}}=\text{6.8 hrs}=\text{6 hr 48 min}[/latex]
[latex]\text{07:45 + 6 hr}=\text{13:45 + 48 min}=\text{14:33 is when physio should expect the patient}[/latex] - [latex]\text{infusion time}=\dfrac{\text{238}}{\text{500}}=\text{0.476 hrs}=\text{29 min}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{784}}{\text{200}}=\text{3.92 hrs}=\text{3 h 55 min hrs}[/latex]
- [latex]\text{infusion time}=\dfrac{\text{675}}{\text{83}}=\text{8.1325 hrs}=\text{8 hr 8 min}[/latex]
The number of drops infusing per minute of an intravenous infusion.
The number identifying the number of drops in 1 mL of fluid for particular IV tubing sets.

