Chapter 11. Solutions

Concentrations as Conversion Factors

Learning Objectives

  1. Apply concentration units as conversion factors.

Concentration can be a conversion factor between the amount of solute and the amount of solution or solvent (depending on the definition of the concentration unit). As such, concentrations can be useful in a variety of stoichiometry problems. In many cases, it is best to use the original definition of the concentration unit; it is that definition that provides the conversion factor.

A simple example of using a concentration unit as a conversion factor is one in which we use the definition of the concentration unit and rearrange; we can do the calculation again as a unit conversion, rather than as a definition. For example, suppose we ask how many moles of solute are present in 0.108 L of a 0.887 M NaCl solution. Because 0.887 M means 0.887 mol/L, we can use this second expression for the concentration as a conversion factor:

0.108\text{ \cancel{L NaCl}}\times\dfrac{0.887\text{ mol NaCl}}{1\text{ \cancel{L NaCl}}}=0.0958\text{ mol NaCl}

(There is an understood 1 in the denominator of the conversion factor.) If we used the definition approach, we get the same answer, but now we are using conversion factor skills. Like any other conversion factor that relates two different types of units, the reciprocal of the concentration can be also used as a conversion factor.

Example 11.6

Using concentration as a conversion factor, how many litres of 2.35 M CuSO4 are needed to obtain 4.88 mol of CuSO4?

Solution

This is a one-step conversion, but the concentration must be written as the reciprocal for the units to work out:

4.88\cancel{\text{ mol }\ce{CuSO4}}\times\dfrac{1\text{ L}}{2.35\cancel{\text{ mol }\ce{CuSO4}}}=2.08\text{ L of solution}

Test Yourself

Using concentration as a conversion factor, how many litres of 0.0444 M CH2O are needed to obtain 0.0773 mol of CH2O?

Answer

1.74 L

Of course, once quantities in moles are available, another conversion can give the mass of the substance, using molar mass as a conversion factor.

Example 11.7

What mass of solute is present in 0.765 L of 1.93 M NaOH?

Solution

This is a two-step conversion, first using concentration as a conversion factor to determine the number of moles and then the molar mass of NaOH (40.0 g/mol) to convert to mass:

0.765\text{ \cancel{L}}\times\dfrac{1.93\text{ \cancel{mol NaOH}}}{\text{\cancel{L} solution}}\times\dfrac{40.0\text{ g NaOH}}{1\text{ \cancel{mol NaOH}}}=59.1\text{ g NaOH}

Test Yourself

What mass of solute is present in 1.08 L of 0.0578 M H2SO4?

Answer

6.12 g

More complex stoichiometry problems using balanced chemical reactions can also use concentrations as conversion factors. For example, suppose the following equation represents a chemical reaction:

2AgNO3(aq) + CaCl2(aq) → 2AgCl(s) + Ca(NO3)2(aq)

If we wanted to know what volume of 0.555 M CaCl2 would react with 1.25 mol of AgNO3, we first use the balanced chemical equation to determine the number of moles of CaCl2 that would react and then use concentration to convert to litres of solution:

1.25\cancel{\text{ mol }\ce{AgNO3}}\times\dfrac{1\cancel{\text{ mol }\ce{CaCl2}}}{2\cancel{\text{ mol }\ce{AgNO3}}}\times\dfrac{1\text{ L solution}}{0.555\cancel{\text{ mol }\ce{CaCl2}}}=1.13\text{ L }\ce{CaCl2}

This can be extended by starting with the mass of one reactant, instead of moles of a reactant.

Example 11.8

What volume of 0.0995 M Al(NO3)3 will react with 3.66 g of Ag according to the following chemical equation?

3Ag(s) + Al(NO3)3(aq) → 3AgNO3 + Al(s)

Solution
Here, we first must convert the mass of Ag to moles before using the balanced chemical equation and then the definition of molarity as a conversion factor:

    \begin{multline*} 3.66\text{ \cancel{g Ag}}\times\dfrac{1\text{ \cancel{mol Ag}}}{107.97\text{ \cancel{g Ag}}}\times \dfrac{1\cancel{\text{ mol }\ce{Al(NO3)3}}}{3\text{ \cancel{mol Ag}}}\times \dfrac{1\text{ L solution}}{0.0995\cancel{\text{ mol }\ce{Al(NO3)3}}} \\ \\ =0.114\text{ L}\hspace{5mm} \end{multline*}

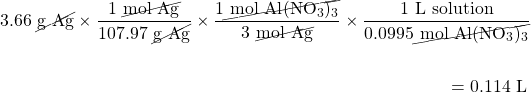
Test Yourself
What volume of 0.512 M NaOH will react with 17.9 g of H2C2O4(s) according to the following chemical equation?

H2C2O4(s) + 2NaOH(aq) → Na2C2O4(aq) + 2H2O(ℓ)

Answer
0.777 L

We can extend our skills even further by recognizing that we can relate quantities of one solution to quantities of another solution. Knowing the volume and concentration of a solution containing one reactant, we can determine how much of another solution of another reactant will be needed using the balanced chemical equation.

Example 11.9

A student takes a precisely measured sample, called an aliquot, of 10.00 mL of a solution of FeCl3. The student carefully adds 0.1074 M Na2C2O4 until all the Fe3+(aq) has precipitated as Fe2(C2O4)3(s). Using a precisely measured tube called a burette, the student finds that 9.04 mL of the Na2C2O4 solution was added to completely precipitate the Fe3+(aq). What was the concentration of the FeCl3 in the original solution? (A precisely measured experiment like this, which is meant to determine the amount of a substance in a sample, is called a titration.) The balanced chemical equation is as follows:

2FeCl3(aq) + 3Na2C2O4(aq) → Fe2(C2O4)3(s) + 6NaCl(aq)

Solution
First we need to determine the number of moles of Na2C2O4 that reacted. We will convert the volume to litres and then use the concentration of the solution as a conversion factor:

9.04\text{ \cancel{mL}}\times \dfrac{1\text{ \cancel{L}}}{1000\text{ \cancel{mL}}}\times \dfrac{0.1074\text{ mol }\ce{Na2C2O4}}{\text{ \cancel{L}}}=0.000971\text{ mol }\ce{Na2C2O4}

Now we will use the balanced chemical equation to determine the number of moles of Fe3+(aq) that were present in the initial aliquot:

0.000971\cancel{\text{ mol }\ce{Na2C2O4}}\times \dfrac{2\text{ mol }\ce{FeCl3}}{3\cancel{\text{ mol }\ce{Na2C2O4}}}=0.000647\text{ mol }\ce{FeCl3}

Then we determine the concentration of FeCl3 in the original solution. Converting 10.00 mL into litres (0.01000 L), we use the definition of molarity directly:

\text{M}=\dfrac{\text{mol}}{\text{L}}=\dfrac{0.000647\text{ mol }\ce{FeCl3}}{0.01000\text{ L}}=0.0647\text{ M }\ce{FeCl3}

Test Yourself
A student titrates 25.00 mL of H3PO4 with 0.0987 M KOH. She uses 54.06 mL to complete the chemical reaction. What is the concentration of H3PO4?

H3PO4(aq) + 3KOH(aq) → K3PO4(aq) + 3H2O

Answer
0.0711 M

When a student performs a titration, a measured amount of one solution is added to another reactant. “Chemistry titration lab” by Kentucky Country Day is licensed under the Creative Commons Attribution-NonCommercial 2.0 Generic.
When a student performs a titration, a measured amount of one solution is added to another reactant.

We have used molarity exclusively as the concentration of interest, but that will not always be the case. The next example shows a different concentration unit being used.

Example 11.10

H2O2 is used to determine the amount of Mn according to this balanced chemical equation:

2MnO4−(aq) + 5H2O2(aq) + 6H+(aq) → 2Mn2+(aq) + 5O2(g) + 8H2O(ℓ)

What mass of 3.00% m/m H2O2 solution is needed to react with 0.355 mol of MnO4−(aq)?

Solution
Because we are given an initial amount in moles, all we need to do is use the balanced chemical equation to determine the number of moles of H2O2 and then convert to find the mass of H2O2. Knowing that the H2O2 solution is 3.00% by mass, we can determine the mass of solution needed:

    \begin{multline*} 0.355\cancel{\text{ mol }\ce{MnO4^-}}\times\dfrac{5\cancel{\text{ mol }\ce{H2O2}}}{2\cancel{\text{ mol }\ce{MnO4^-}}}\times\dfrac{34.02\cancel{\text{ g }\ce{H2O2}}}{1\cancel{\text{ mol }\ce{H2O2}}}\times\dfrac{100\text{ g solution}}{3\cancel{\text{ g }\ce{H2O2}}} \\ \\ =1006\text{ g solution}\hspace{5mm} \end{multline*}

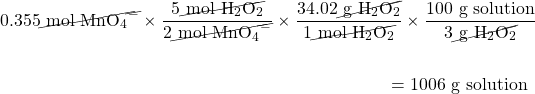
The first conversion factor comes from the balanced chemical equation, the second conversion factor is the molar mass of H2O2, and the third conversion factor comes from the definition of percentage concentration by mass.

Test Yourself
Use the balanced chemical reaction for MnO4− and H2O2 to determine what mass of O2 is produced if 258 g of 3.00% m/m H2O2 is reacted with MnO4−.

Answer
7.28 g

Key Takeaways

  • Know how to apply concentration units as conversion factors.

Exercises

Questions

  1. Using concentration as a conversion factor, how many moles of solute are in 3.44 L of 0.753 M CaCl2?
  2. Using concentration as a conversion factor, how many moles of solute are in 844 mL of 2.09 M MgSO4?
  3. Using concentration as a conversion factor, how many litres are needed to provide 0.822 mol of NaBr from a 0.665 M solution?
  4. Using concentration as a conversion factor, how many litres are needed to provide 2.500 mol of (NH2)2CO from a 1.087 M solution?
  5. What is the mass of solute in 24.5 mL of 0.755 M CoCl2?
  6. What is the mass of solute in 3.81 L of 0.0232 M Zn(NO3)2?
  7. What volume of solution is needed to provide 9.04 g of NiF2 from a 0.332 M solution?
  8. What volume of solution is needed to provide 0.229 g of CH2O from a 0.00560 M solution?
  9. What volume of 3.44 M HCl will react with 5.33 mol of CaCO3?

    2HCl + CaCO3 → CaCl2 + H2O + CO2

  10. What volume of 0.779 M NaCl will react with 40.8 mol of Pb(NO3)2?

    Pb(NO3)2 + 2NaCl → PbCl2 + 2NaNO3

  11. What volume of 0.905 M H2SO4 will react with 26.7 mL of 0.554 M NaOH?

    H2SO4 + 2NaOH → Na2SO4 + 2H2O

  12. What volume of 1.000 M Na2CO3 will react with 342 mL of 0.733 M H3PO4?

    3Na2CO3 + 2H3PO4 → 2Na3PO4 + 3H2O + 3CO2

  13. It takes 23.77 mL of 0.1505 M HCl to titrate with 15.00 mL of Ca(OH)2. What is the concentration of Ca(OH)2? You will need to write the balanced chemical equation first.
  14. It takes 97.62 mL of 0.0546 M NaOH to titrate a 25.00 mL sample of H2SO4. What is the concentration of H2SO4? You will need to write the balanced chemical equation first.
  15. It takes 4.667 mL of 0.0997 M HNO3 to dissolve some solid Cu. What mass of Cu can be dissolved?

    Cu + 4HNO3(aq) → Cu(NO3)2(aq) + 2NO2 + 2H2O

  16. It takes 49.08 mL of 0.877 M NH3 to dissolve some solid AgCl. What mass of AgCl can be dissolved?

    AgCl(s) + 4NH3(aq) → Ag(NH3)4Cl(aq)

  17. What mass of 3.00% H2O2 is needed to produce 66.3 g of O2(g)?

    2H2O2(aq) → 2H2O(ℓ) + O2(g)

  18. A 0.75% solution of Na2CO3 is used to precipitate Ca2+ ions from solution. What mass of solution is needed to precipitate 40.7 L of solution with a concentration of 0.0225 M Ca2+(aq)?

    Na2CO3(aq) + Ca2+(aq) → CaCO3(s) + 2Na+(aq)

Answers

  1. 2.59 mol
  1. 1.24 L
  1. 2.40 g
  1. 0.282 L
  1. 3.10 L
  1. 8.17 mL
  1. 0.1192 M
  1. 7.39 mg
  1. 4.70 kg

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introductory Chemistry - 1st Canadian Edition Copyright © 2014 by Jessie A. Key is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book