Chapter 7. Energy and Chemistry
Hess’s Law
Learning Objectives
- Learn how to combine chemical equations and their enthalpy changes.
Now that we understand that chemical reactions occur with a simultaneous change in energy, we can apply the concept more broadly. To start, remember that some chemical reactions are rather difficult to perform. For example, consider the combustion of carbon to make carbon monoxide:
![]()
In reality, this is extremely difficult to do; given the opportunity, carbon will react to make another compound, carbon dioxide:
![]()
Is there a way around this? Yes. It comes from the understanding that chemical equations can be treated like algebraic equations, with the arrow acting like the equals sign. Like algebraic equations, chemical equations can be combined, and if the same substance appears on both sides of the arrow, it can be cancelled out (much like a spectator ion in ionic equations). For example, consider these two reactions:
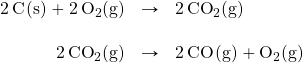
If we added these two equations by combining all the reactants together and all the products together, we would get:
![]()
We note that 2CO2(g) appears on both sides of the arrow, so they cancel:
![]()
We also note that there are 2 mol of O2 on the reactant side, and 1 mol of O2 on the product side. We can cancel 1 mol of O2 from both sides:
![]()
What do we have left?
![]()
This is the reaction we are looking for! So by algebraically combining chemical equations, we can generate new chemical equations that may not be feasible to perform.
What about the enthalpy changes? Hess’s law states that when chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way. Two corollaries immediately present themselves:
- If a chemical reaction is reversed, the sign on ΔH is changed.
- If a multiple of a chemical reaction is taken, the same multiple of the ΔH is taken as well.
What are the equations being combined? The first chemical equation is the combustion of C, which produces CO2:
![]()
This reaction is two times the reaction to make CO2 from C(s) and O2(g), whose enthalpy change is known:
![]()
According to the first corollary, the first reaction has an energy change of two times −393.5 kJ, or −787.0 kJ:
![]()
The second reaction in the combination is related to the combustion of CO(g):
![]()
The second reaction in our combination is the reverse of the combustion of CO. When we reverse the reaction, we change the sign on the ΔH:
![]()
Now that we have identified the enthalpy changes of the two component chemical equations, we can combine the ΔH values and add them:
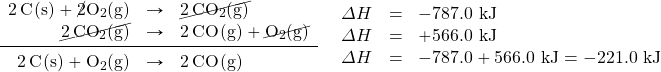
Hess’s law is very powerful. It allows us to combine equations to generate new chemical reactions whose enthalpy changes can be calculated, rather than directly measured.
Example 7.14
Problem
Determine the enthalpy change of:
![]()
from these reactions:
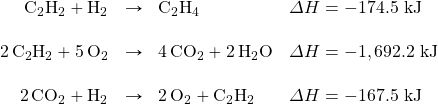
Solution
We will start by writing chemical reactions that put the correct number of moles of the correct substance on the proper side. For example, our desired reaction has C2H4 as a reactant, and only one reaction from our data has C2H4. However, it has C2H4 as a product. To make it a reactant, we need to reverse the reaction, changing the sign on the ΔH:
![]()
We need CO2 and H2O as products. The second reaction has them on the proper side, so let us include one of these reactions (with the hope that the coefficients will work out when all our reactions are added):
![]()
We note that we now have 4 mol of CO2 as products; we need to get rid of 2 mol of CO2. The last reaction has 2CO2 as a reactant. Let us use it as written:
![]()
We combine these three reactions, modified as stated:
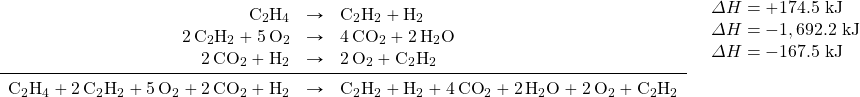
What cancels? 2C2H2, H2, 2O2, and 2CO2. What is left is:
![]()
Which is the reaction we are looking for. The ΔH of this reaction is the sum of the three ΔH values:
![]()
Test Yourself
Given the following thermochemical equations:
![]()
Determine ΔH for:
![]()
Answer
+136 kJ
Key Takeaways
- Hess’s law allows us to combine reactions algebraically and then combine their enthalpy changes the same way.
Exercises
Questions
- Define Hess’s law.
- What does Hess’s law require us to do to the ΔH of a thermochemical equation if we reverse the equation?
- If the ΔH for C2H4 + H2 → C2H6 is −65.6 kJ, what is the ΔH for the reaction C2H6 → C2H4 + H2?
- If the ΔH for 2Na + Cl2 → 2NaCl is −772 kJ, what is the ΔH for the reaction 2NaCl → 2Na + Cl2?
- If the ΔH for C2H4 + H2 → C2H6 is −65.6 kJ, what is the ΔH for the reaction 2C2H4 + 2H2 → 2C2H6?
- If the ΔH for 2C2H6 + 7O2 → 4CO2 + 6H2O is −2,650 kJ, what is the ΔH for the reaction 6C2H6 + 21O2 → 12CO2 + 18H2O?
- The ΔH for C2H4 + H2O → C2H5OH is −44 kJ. What is the ΔH for the reaction 2C2H5OH → 2C2H4 + 2H2O?
- The ΔH for N2 + O2 → 2NO is 181 kJ. What is the ΔH for the reaction
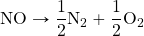 ?
? - Determine the ΔH for the reaction Cu + Cl2 → CuCl2 given these data:
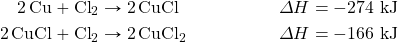
- Determine ΔH for the reaction 2CH4 → 2H2 + C2H4 given these data:
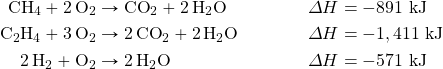
- Determine ΔH for the reaction Fe2(SO4)3 → Fe2O3 + 3SO3 given these data:
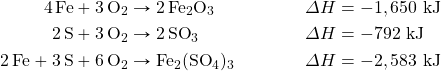
- Determine ΔH for the reaction CaCO3 → CaO + CO2 given these data:
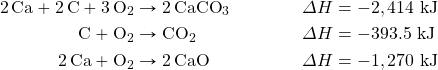
Answers
- If chemical equations are combined, their energy changes are also combined.
- ΔH = 65.6 kJ
- ΔH = −131.2 kJ
- ΔH = 88 kJ
- ΔH = −220 kJ
- ΔH = 570 kJ
When chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way.

