Chapter 18. Chemical Thermodynamics
Entropy and the Second Law of Thermodynamics
Jessie A. Key
Learning Objectives
- To gain an understanding of the term entropy.
- To gain an understanding of the Boltzmann equation and the term microstates.
- To be able to estimate change in entropy qualitatively.
To assess the spontaneity of a process we must use a thermodynamic quantity known as entropy (S). The second law of thermodynamics states that a spontaneous process will increase the entropy of the universe. But what exactly is entropy? Entropy is typically defined as either the level of randomness (or disorder) of a system or a measure of the energy dispersal of the molecules in the system. These definitions can seem a bit vague or unclear when you are first learning thermodynamics, but we will try to clear this up in the following subsections.
The Molecular Interpretation of Entropy
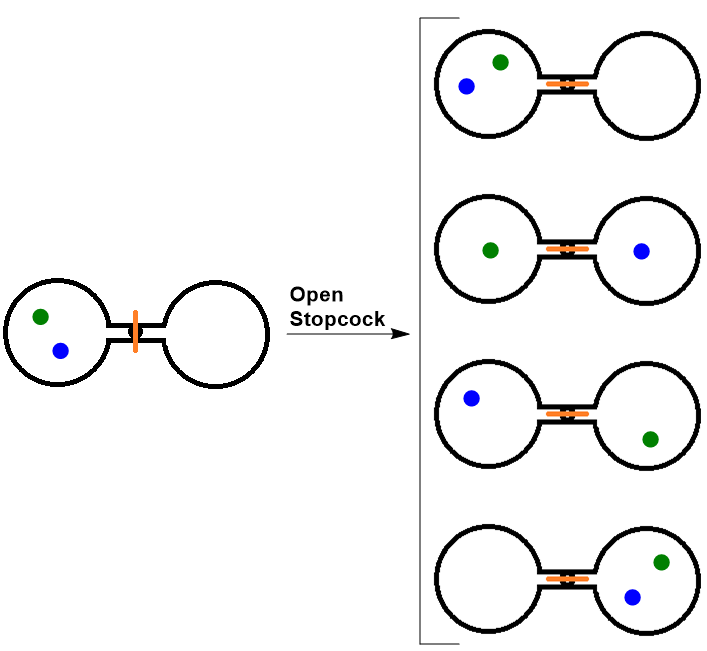
Consider the following system, where two flasks are sealed together and connected by a stopcock (see Figure 18.1 “Two-Atom, Double-Flask Diagram”). In this system, we have placed two atoms of gas, one green and one blue. At first, both atoms are contained in only the left flask. When the stopcock is opened, both atoms are free to move around randomly in both flasks. If we were to take snapshots over time, we would see that these atoms can have four possible arrangements. The likelihood of all atoms being found in their original flask, in this case, is only 1 in 4. If we increased the number of atoms, we would see that the probability of finding all of the atoms in the original flask would decrease dramatically following (½)n, where n is the number of atoms.
Thus we can say that it is entropically favoured for the gas to spontaneously expand and distribute between the two flasks, because the resulting increase in the number of possible arrangements is an increase in the randomness/disorder of the system.
The Boltzmann Equation

Ludwig Boltzmann (1844–1906) pioneered the concept that entropy could be calculated by examining the positions and energies of molecules. He developed an equation, known as the Boltzmann equation, which relates entropy to the number of microstates (W):
![]()
where k is the Boltzmann constant (1.38 × 10−23 J/K), and W is the number of microstates.
Microstates is a term used to describe the number of different possible arrangements of molecular position and kinetic energy at a particular thermodynamic state. A process that gives an increase in the number of microstates therefore increases the entropy.
Qualitative Estimates of Entropy Change
We can estimate changes in entropy qualitatively for some simple processes using the definition of entropy discussed earlier and incorporating Boltzmann’s concept of microstates.
As a substance is heated, it gains kinetic energy, resulting in increased molecular motion and a broader distribution of molecular speeds. This increases the number of microstates possible for the system. Increasing the number of molecules in a system also increases the number of microstates, as now there are more possible arrangements of the molecules. As well, increasing the volume of a substance increases the number of positions where each molecule could be, which increases the number of microstates. Therefore, any change that results in a higher temperature, more molecules, or a larger volume yields an increase in entropy.
Key Takeaways
- Entropy is the level of randomness (or disorder) of a system. It could also be thought of as a measure of the energy dispersal of the molecules in the system.
- Microstates are the number of different possible arrangements of molecular position and kinetic energy at a particular thermodynamic state.
- Any change that results in a higher temperature, more molecules, or a larger volume yields an increase in entropy.
Media Attributions
- “Portrait of Ludwig Boltzmann” © American Institute of Physics, Emilio Segrè Visual Archives, Segrè Collection is licensed under a Public Domain license
The level of randomness (or disorder) of a system, or a measure of the energy dispersal of the molecules in the system.
A term used to describe different possible arrangements of molecular position and kinetic energy, at a particular thermodynamic state.

