Chapter 17. Kinetics
Rate Laws
Jessie A. Key
Learning Objectives
- To gain an understanding of rate laws and determine rate laws from initial rates.
- To gain an understanding of and the ability to determine reaction orders (including units).
The mathematical relationship of reaction rate with reactant concentrations is known as the rate law. This relationship may rely more heavily on the concentration of one particular reactant, and the resulting rate law may include some, all, or none of the reactant species involved in the reaction.
For the following hypothetical reaction
![]()
the rate law can be expressed as:
![]()
The proportionality constant, k, is known as the rate constant and is specific for the reaction shown at a particular temperature. The rate constant changes with temperature, and its units depend on the sum of the concentration term exponents in the rate law. The exponents (y and z) must be experimentally determined and do not necessarily correspond to the coefficients in the balanced chemical equation.
Reaction Order
The sum of the concentration term exponents in a rate law equation is known as its reaction order. We can also refer to the relationship for each reactant in terms of its exponent as an order.
For the following reaction between nitrogen dioxide and carbon monoxide:
NO2(g) + CO(g) → NO(g) + CO2(g)
The rate law is experimentally determined to be: rate = k[NO2]2
Therefore, we would say that the overall reaction order for this reaction is second-order (the sum of all exponents in the rate law is 2), but zero-order for [CO] and second-order for [NO2].
The reaction order is most often a whole number such as 0, 1, or 2; however, there are instances where the reaction order may be a fraction or even a negative value.
Earlier, it was mentioned that the units of the rate constant depend on the order of the reaction. Let’s quickly examine why this occurs. A simplified rate law can be expressed generically in the following way:
![Rendered by QuickLaTeX.com \begin{align*} \text{rate}&=k[\text{reactant}]^y \\ \\ \text{Units of rate}&=\text{(units of rate constant)}\text{(units of concentration)}^y \\ \\ \text{Units of rare constant}&=\dfrac{\text{Units of rate}}{(\text{Units of concentration})^y} \\ \\ &=\dfrac{\text{M/s}}{\text{M}^y} \end{align*}](https://opentextbc.ca/introductorychemistry/wp-content/ql-cache/quicklatex.com-ae0a79ff85e572c7d2e3a537a6c01ab5_l3.png)
Therefore, the units of the rate constant should be:
| Reaction Order | Units of rate constant |
|---|---|
| Zero-order | M s−1 |
| First-order | s−1 |
| Second-order | L mol−1 s−1 |
Determining Rate Laws from Initial Rates
The rate law can be determined experimentally using the method of initial rates, where the instantaneous reaction rate is measured immediately on mixing the reactants. The process is repeated over several runs or trials, varying the concentration one reactant at a time. These runs can then be compared to elucidate how changing the concentration of each reactant affects the initial rate.
Example 17.3
The initial rate of reaction for the reaction E + F → G was measured at three different initial concentrations of reactants as shown in the table.
- Determine the rate law of the reaction.
- Determine the rate constant.
| Trial | Initial Rate (mol L−1 s−1) |
[E] (mol L−1) | [F] (mol L−1) |
| 1 | 2.73 × 10−5 | 0.100 | 0.100 |
| 2 | 5.47 × 10−5 | 0.200 | 0.100 |
| 3 | 2.71 × 10−5 | 0.100 | 0.200 |
Solution
- Comparing trials 1 and 2, [E] is doubled, while [F] and the rate constant are held constant. This comparison will allow us to determine the order of reactant E:
![Rendered by QuickLaTeX.com \begin{align*} \dfrac{\text{initial rate 2}}{\text{initial rate 1}}&=\left(\dfrac{[\text{E}] \ _2}{[\text{E}] \ _1}\right)^y \\ \\ \dfrac{5.47\times10^{-5}\text{M s}^{-1}}{2.73\times 10^{-5}\text{ M s}^{-1}}&=\left(\dfrac{0.200\text{ M}}{0.100\text{ M}}\right)^y \\ \\ 2.00&=2.00^y \\ \\ y&=1 \end{align*}](https://opentextbc.ca/introductorychemistry/wp-content/ql-cache/quicklatex.com-1cf93e9cfd33a5f820ac1b1b8ff7036a_l3.png)
Therefore, the reaction is first order with respect to [E].
Comparing trials 1 and 3, [F] is doubled, while [E] and the rate constant are held constant. This comparison will allow us to determine the order of reactant F:
![Rendered by QuickLaTeX.com \begin{align*} \dfrac{\text{initial rate 3}}{\text{initial rate 1}}&=\left(\dfrac{[\text{F}] \ _3}{[\text{F}] \ _1}\right)^z \\ \\ \dfrac{2.71\times 10^{-5}\text{ M s}^{-1}}{2.73\times 10^{-5}\text{ M s}^{-1}}&=\left(\dfrac{0.200\text{ M}}{0.100\text{ M}}\right)^z \\ \\ 0.993&=2.00^z \\ \\ z&=0 \end{align*}](https://opentextbc.ca/introductorychemistry/wp-content/ql-cache/quicklatex.com-fc629a4c89fa99c7ff502364a08c0bb2_l3.png)
Therefore, the reaction is zero order with respect to [F].
The rate law can now be written as:
![Rendered by QuickLaTeX.com \text{rate}=k[\text{E}]^1](https://opentextbc.ca/introductorychemistry/wp-content/ql-cache/quicklatex.com-f93c73ecda6bab1d54a1ffc925506cdb_l3.png)
- Using the rate law we have just determined, substitute in the initial concentration values and initial rate for any trial and solve for the rate constant:
![Rendered by QuickLaTeX.com \text{rate}=k[\text{E}]^1](https://opentextbc.ca/introductorychemistry/wp-content/ql-cache/quicklatex.com-f93c73ecda6bab1d54a1ffc925506cdb_l3.png)
Using Trial 1:
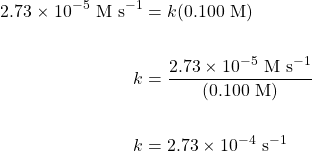
Key Takeaways
- The rate law is a mathematical relationship obtained by comparing reaction rates with reactant concentrations.
- The reaction order is the sum of the concentration term exponents in a rate law equation.
- A reaction’s rate law may be determined by the initial rates method.

