Chapter 6. Gases
Gas Mixtures
Learning Objectives
- Learn Dalton’s law of partial pressures.
One of the properties of gases is that they mix with each other. When they do so, they become a solution—a homogeneous mixture. Some of the properties of gas mixtures are easy to determine if we know the composition of the gases in the mix.
In gas mixtures, each component in the gas phase can be treated separately. Each component of the mixture shares the same temperature and volume. (Remember that gases expand to fill the volume of their container; gases in a mixture do that as well.) However, each gas has its own pressure. The partial pressure of a gas, Pi, is the pressure that an individual gas in a mixture has. Partial pressures are expressed in torr, millimetres of mercury, or atmospheres like any other gas pressure; however, we use the term pressure when talking about pure gases and the term partial pressure when we are talking about the individual gas components in a mixture.
Dalton’s law of partial pressures states that the total pressure of a gas mixture, Ptot, is equal to the sum of the partial pressures of the components, Pi:
![]()
Although this may seem to be a trivial law, it reinforces the idea that gases behave independently of each other.
Example 6.15
Problem
A mixture of H2 at 2.33 atm and N2 at 0.77 atm is in a container. What is the total pressure in the container?
Solution
Dalton’s law of partial pressures states that the total pressure is equal to the sum of the partial pressures. We simply add the two pressures together:
Ptot = 2.33 atm + 0.77 atm = 3.10 atm
Test Yourself
Air can be thought of as a mixture of N2 and O2. In 760 torr of air, the partial pressure of N2 is 608 torr. What is the partial pressure of O2?
Answer
152 torr
Example 6.16
Problem
A 2.00 L container with 2.50 atm of H2 is connected to a 5.00 L container with 1.90 atm of O2 inside. The containers are opened, and the gases mix. What is the final pressure inside the containers?
Solution
Because gases act independently of each other, we can determine the resulting final pressures using Boyle’s law and then add the two resulting pressures together to get the final pressure. The total final volume is 2.00 L + 5.00 L = 7.00 L. First, we use Boyle’s law to determine the final pressure of H2:
![]()
Solving for P2, we get:
![]()
Now we do that same thing for the O2:
![]()
The total pressure is the sum of the two resulting partial pressures:
![]()
Test Yourself
If 0.75 atm of He in a 2.00 L container is connected to a 3.00 L container with 0.35 atm of Ne and the connection between the containers is opened, what is the resulting total pressure?
Answer
0.51 atm
One of the reasons we have to deal with Dalton’s law of partial pressures is that gases are frequently collected by bubbling through water. As we will see in Chapter 10 “Solids and Liquids”, liquids are constantly evaporating into a vapour until the vapour achieves a partial pressure characteristic of the substance and the temperature. This partial pressure is called a vapour pressure. Table 6.2 “Vapour Pressure of Water versus Temperature” lists the vapour pressures of H2O versus temperature. Note that if a substance is normally a gas under a given set of conditions, the term partial pressure is used; the term vapour pressure is reserved for the partial pressure of a vapour when the liquid is the normal phase under a given set of conditions.
| Temperature (°C) | Vapour Pressure (torr) |
|---|---|
| 5 | 6.54 |
| 10 | 9.21 |
| 15 | 12.79 |
| 20 | 17.54 |
| 21 | 18.66 |
| 22 | 19.84 |
| 23 | 21.08 |
| 24 | 22.39 |
| 25 | 23.77 |
| 30 | 31.84 |
| 35 | 42.20 |
| 40 | 55.36 |
| 50 | 92.59 |
| 60 | 149.5 |
| 70 | 233.8 |
| 80 | 355.3 |
| 90 | 525.9 |
| 100 | 760.0 |
Any time a gas is collected over water, the total pressure is equal to the partial pressure of the gas plus the vapour pressure of water. This means that the amount of gas collected will be less than the total pressure suggests.
Example 6.17
Problem
Hydrogen gas is generated by the reaction of nitric acid and elemental iron. The gas is collected in an inverted 2.00 L container immersed in a pool of water at 22°C. At the end of the collection, the partial pressure inside the container is 733 torr. How many moles of H2 gas were generated?
Solution
We need to take into account that the total pressure includes the vapour pressure of water. According to Table 6.2 “Vapour Pressure of Water versus Temperature,” the vapour pressure of water at 22°C is 19.84 torr. According to Dalton’s law of partial pressures, the total pressure equals the sum of the pressures of the individual gases, so:
733 torr = PH2 + PH2O = PH2 + 19.84 torr
We solve by subtracting:
PH2 = 713 torr
Now we can use the ideal gas law to determine the number of moles (remembering to convert the temperature to kelvins, making it 295 K):
![]()
All the units cancel except for mol, which is what we are looking for. So:
n = 0.0775 mol H2 collected
Test Yourself
CO2, generated by the decomposition of CaCO3, is collected in a 3.50 L container over water. If the temperature is 50°C and the total pressure inside the container is 833 torr, how many moles of CO2 were generated?
Answer
0.129 mol
Finally, we introduce a new unit that can be useful, especially for gases. The mole fraction, χi, is the ratio of the number of moles of component i in a mixture divided by the total number of moles in the sample:
![]()
(χ is the lowercase Greek letter chi.) Note that mole fraction is not a percentage; its values range from 0 to 1. For example, consider the combination of 4.00 g of He and 5.0 g of Ne. Converting both to moles, we get:
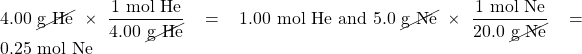
The total number of moles is the sum of the two mole amounts:
total moles = 1.00 mol + 0.025 mol = 1.25 mol
The mole fractions are simply the ratio of each mole amount to the total number of moles, 1.25 mol:
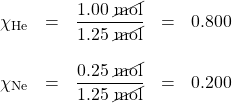
The sum of the mole fractions equals exactly 1.
For gases, there is another way to determine the mole fraction. When gases have the same volume and temperature (as they would in a mixture of gases), the number of moles is proportional to partial pressure, so the mole fractions for a gas mixture can be determined by taking the ratio of partial pressure to total pressure:
![]()
This expression allows us to determine mole fractions without calculating the moles of each component directly.
Example 6.18
Problem
A container has a mixture of He at 0.80 atm and Ne at 0.60 atm. What is the mole fraction of each component?
Solution
According to Dalton’s law, the total pressure is the sum of the partial pressures:
Ptot = 0.80 atm + 0.60 atm = 1.40 atm
The mole fractions are the ratios of the partial pressure of each component to the total pressure:

Again, the sum of the mole fractions is exactly 1.
Test Yourself
What are the mole fractions when 0.65 atm of O2 and 1.30 atm of N2 are mixed in a container?
Answer
![]()
Food and Drink App: Carbonated Beverages
Carbonated beverages—sodas, beer, sparkling wines—have one thing in common: they have CO2 gas dissolved in them in such sufficient quantities that it affects the drinking experience. Most people find the drinking experience pleasant—indeed, in the United States alone, over 1.5 × 109 gal of soda are consumed each year, which is almost 50 gal per person! This figure does not include other types of carbonated beverages, so the total consumption is probably significantly higher.
All carbonated beverages are made in one of two ways. First, the flat beverage is subjected to a high pressure of CO2 gas, which forces the gas into solution. The carbonated beverage is then packaged in a tightly sealed package (usually a bottle or a can) and sold. When the container is opened, the CO2 pressure is released, resulting in the well-known hiss, and CO2 bubbles come out of solution (Figure 6.5 “Opening a Carbonated Beverage”). This must be done with care: if the CO2 comes out too violently, a mess can occur!

The second way a beverage can become carbonated is by the ingestion of sugar by yeast, which then generates CO2 as a digestion product. This process is called fermentation. The overall reaction is:
C6H12O6(aq) → 2C2H5OH(aq) + 2CO2(aq)
When this process occurs in a closed container, the CO2 produced dissolves in the liquid, only to be released from solution when the container is opened. Most fine sparkling wines and champagnes are turned into carbonated beverages this way. Less-expensive sparkling wines are made like sodas and beer, with exposure to high pressures of CO2 gas.
Key Takeaways
- The pressure of a gas in a gas mixture is termed the partial pressure.
- Dalton’s law of partial pressure states that the total pressure in a gas mixture is the sum of the individual partial pressures.
- Collecting gases over water requires that we take the vapour pressure of water into account.
- Mole fraction is another way to express the amounts of components in a mixture.
Exercises
Questions
- What is the total pressure of a gas mixture containing these partial pressures: PN2 = 0.78 atm, PH2 = 0.33 atm, and PO2 = 1.59 atm?
- What is the total pressure of a gas mixture containing these partial pressures: PNe = 312 torr, PHe = 799 torr, and PAr = 831 torr?
- In a gas mixture of He and Ne, the total pressure is 335 torr and the partial pressure of He is 0.228 atm. What is the partial pressure of Ne?
- In a gas mixture of O2 and N2, the total pressure is 2.66 atm and the partial pressure of O2 is 888 torr. What is the partial pressure of N2?
- A 3.55 L container has a mixture of 56.7 g of Ar and 33.9 g of He at 33°C. What are the partial pressures of the gases and the total pressure inside the container?
- A 772 mL container has a mixture of 2.99 g of H2 and 44.2 g of Xe at 388 K. What are the partial pressures of the gases and the total pressure inside the container?
- A sample of O2 is collected over water in a 5.00 L container at 20°C. If the total pressure is 688 torr, how many moles of O2 are collected?
- A sample of H2 is collected over water in a 3.55 L container at 50°C. If the total pressure is 445 torr, how many moles of H2 are collected?
- A sample of CO is collected over water in a 25.00 L container at 5°C. If the total pressure is 0.112 atm, how many moles of CO are collected?
- A sample of NO2 is collected over water in a 775 mL container at 25°C. If the total pressure is 0.990 atm, how many moles of NO2 are collected?
- A sample of NO is collected over water in a 75.0 mL container at 25°C. If the total pressure is 0.495 atm, how many grams of NO are collected?
- A sample of ClO2 is collected over water in a 0.800 L container at 15°C. If the total pressure is 1.002 atm, how many grams of ClO2 are collected?
- Determine the mole fractions of each component when 44.5 g of He is mixed with 8.83 g of H2.
- Determine the mole fractions of each component when 9.33 g of SO2 is mixed with 13.29 g of SO3.
- In a container, 4.56 atm of F2 is combined with 2.66 atm of Cl2. What is the mole fraction of each component?
- In a container, 77.3 atm of SiF4 are mixed with 33.9 atm of O2. What is the mole fraction of each component?
Answers
- 2.70 atm
- 162 torr, or 0.213 atm
- PAr = 10.0 atm; PHe = 59.9 atm; Ptot = 69.9 atm
- 0.183 mol
- 0.113 mol
- 0.0440 g
Media Attributions
- “Champagne uncorking” by Niels Noordhoek © CC BY-SA (Attribution ShareAlike)
The pressure that an individual gas in a mixture has.
The total pressure of a gas mixture, P_tot, is equal to the sum of the partial pressures of the components, P_i.
The partial pressure exerted by evaporation of a liquid.
The ratio of the number of moles of a component to the total number of moles in a system.

