Chapter 2. Measurements
Expressing Units
Learning Objectives
- Learn the units that go with various quantities.
- Express units using their abbreviations.
- Make new units by combining numerical prefixes with units.
A number indicates “how much,” but the unit indicates “of what.” The “of what” is important when communicating a quantity. For example, if you were to ask a friend how close you are to Lake Erie and your friend says “six,” then your friend isn’t giving you complete information. Six what? Six miles? Six inches? Six city blocks? The actual distance to the lake depends on what units you use.
Chemistry, like most sciences, uses the International System of Units, or SI for short. (The letters SI stand for the French “le Système International d’unités.”) SI specifies certain units for various types of quantities, based on seven fundamental units for various quantities. We will use most of the fundamental units in chemistry. Initially, we will deal with three fundamental units. The metre (m) is the SI unit of length. It is a little longer than a yard (see Figure 2.4 “The Metre”). The SI unit of mass is the kilogram (kg), which is about 2.2 pounds (lb). The SI unit of time is the second (s).

To express a quantity, you need to combine a number with a unit. If you have a length that is 2.4 m, then you express that length as simply 2.4 m. A time of 15,000 s can be expressed as 1.5 × 104 s in scientific notation.
Sometimes, a given unit is not an appropriate size to easily express a quantity. For example, the width of a human hair is very small, and it doesn’t make much sense to express it in metres. SI also defines a series of numerical prefixes that refer to multiples or fractions of a fundamental unit to make a unit more conveniently sized for a specific quantity. Table 2.4 “Multiplicative Prefixes for SI Units” lists the prefixes, their abbreviations, and their multiplicative factors. Some of the prefixes, such as kilo-, mega-, and giga-, represent more than one of the fundamental unit, while other prefixes, such as centi-, milli-, and micro-, represent fractions of the original unit. Note, too, that once again we are using powers of 10. Each prefix is a multiple of or fraction of a power of 10.
| Prefix | Abbreviation | Multiplicative Amount |
|---|---|---|
| giga- | G | 1,000,000,000 × |
| mega- | M | 1,000,000 × |
| kilo- | k | 1,000 × |
| deci- | d | |
| centi- | c | |
| milli- | m | |
| micro- | μ[1] | |
| nano- | n | |
| pico- | p |
To use the fractions to generate new units, simply combine the prefix with the unit itself; the abbreviation for the new unit is the combination of the abbreviation for the prefix and the abbreviation of the unit. For example, the kilometre (km) is 1,000 × metre, or 1,000 m. Thus, 5 kilometres (5 km) is equal to 5,000 m. Similarly, a millisecond (ms) is ![]() × second, or one one-thousandth of a second. Thus, 25 ms is 25 thousandths of a second. You will need to become proficient in combining prefixes and units. (You may recognize that one of our fundamental units, the kilogram, automatically has a prefix-unit combination, the kilogram. The word kilogram means 1,000 g.)
× second, or one one-thousandth of a second. Thus, 25 ms is 25 thousandths of a second. You will need to become proficient in combining prefixes and units. (You may recognize that one of our fundamental units, the kilogram, automatically has a prefix-unit combination, the kilogram. The word kilogram means 1,000 g.)
In addition to the fundamental units, SI also allows for derived units based on a fundamental unit or units. There are many derived units used in science. For example, the derived unit for area comes from the idea that area is defined as width times height. Because both width and height are lengths, they both have the fundamental unit of metre, so the unit of area is metre × metre, or metre2 (m2). This is sometimes spoken as “square metres.” A unit with a prefix can also be used to derive a unit for area, so we can also have cm2, mm2, or km2 as acceptable units for area.
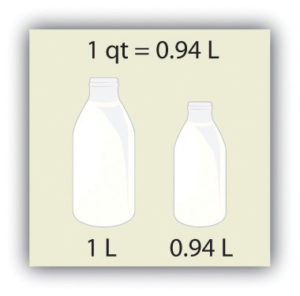
Volume is defined as length times width times height, so it has units of metre × metre × metre or metre3 (m3), sometimes spoken as “cubic metres.” The cubic metre is a rather large unit, however, so another unit is defined that is somewhat more manageable: the litre (L). A litre is one one-thousandth of a cubic metre and is a little more than 1 quart in volume (see Figure 2.5 “The Litre”). Prefixes can also be used with the litre unit, so we can speak of millilitres (one one-thousandth of a litre; mL) and kilolitres (1,000 L; kL).
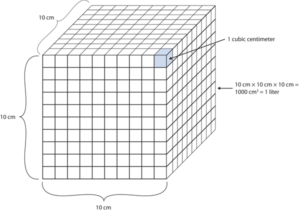
Another definition of a litre is one-tenth of a metre cubed. Because one-tenth of a metre is 10 cm, then a litre is equal to 1,000 cm3 (Figure 2.6 “The Size of 1 Litre”). Because 1 L equals 1,000 mL, we conclude that 1 mL equals 1 cm3; thus, these units are interchangeable.
Units not only are multiplied together but also can be divided. For example, if you are travelling at one metre for every second of time elapsed, your velocity is 1 metre per second, or 1 m/s. The word per implies division, so velocity is determined by dividing a distance quantity by a time quantity. Other units for velocity include kilometres per hour (km/h) or even micrometres per nanosecond (μm/ns). Later, we will see other derived units that can be expressed as fractions.
Example 2.15
Problems
- A human hair has a diameter of about 6.0 × 10−5 m. Suggest an appropriate unit for this measurement and write the diameter of a human hair in terms of that unit.
- What is the velocity of a car if it goes 25 m in 5.0 s?
Solutions
- The scientific notation 10−5 is close to 10−6, which defines the micro- prefix. Let us use micrometres as the unit for hair diameter. The number 6.0 × 10−5 can be written as 60 × 10−6, and a micrometre is 10−6 m, so the diameter of a human hair is about 60 μm.
- If velocity is defined as a distance quantity divided by a time quantity, then velocity is 25 metres/5.0 seconds. Dividing the numbers gives us 25 ÷ 5.0 = 5.0, and dividing the units gives us metres/second, or m/s. The velocity is 5.0 m/s.
Test Yourself
- Express the volume of an Olympic-sized swimming pool, 2,500,000 L, in more appropriate units.
- A common garden snail moves about 6.1 m in 30 min. What is its velocity in metres per minute (m/min)?
Answers
- 2.5 ML
- 0.203 m/min
Key Takeaways
- Numbers tell “how much,” and units tell “of what.”
- Chemistry uses a set of fundamental units and derived units from SI units.
- Chemistry uses a set of prefixes that represent multiples or fractions of units.
- Units can be multiplied and divided to generate new units for quantities.
Exercises
Questions
- Identify the unit in each quantity.
- 2 boxes of crayons
- 3.5 grams of gold
- Identify the unit in each quantity.
- 32 oz of cheddar cheese
- 0.045 cm3 of water
- Identify the unit in each quantity.
- 9.58 s (the current world record in the 100 m dash)
- 6.14 m (the current world record in the pole vault)
- Identify the unit in each quantity.
- 2 dozen eggs
- 2.4 km/s (the escape velocity of the moon, which is the velocity you need at the surface to escape the moon’s gravity)
- Indicate what multiplier each prefix represents.
- k
- m
- M
- Indicate what multiplier each prefix represents.
- c
- G
- μ
- Give the prefix that represents each multiplier.
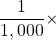
- 1,000 ×
- 1,000,000,000 ×
- Give the prefix that represents each multiplier.
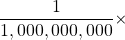
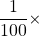
- 1,000,000 ×
- Complete the following table with the missing information.
Unit Abbreviation kilosecond mL Mg centimetre - Complete the following table with the missing information.
Unit Abbreviation kilometre per second second cm3 μL nanosecond - Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 3.44 × 10−6 s
- 3,500 L
- 0.045 m
- Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 0.000066 m/s (Hint: you need consider only the unit in the numerator.)
- 4.66 × 106 s
- 7,654 L
- Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 43,600 mL
- 0.0000044 m
- 1,438 ms
- Express each quantity in a more appropriate unit. There may be more than one acceptable answer.
- 0.000000345 m3
- 47,000,000 mm3
- 0.00665 L
- Multiplicative prefixes are used for other units as well, such as computer memory. The basic unit of computer memory is the byte (b). What is the unit for one million bytes?
- You may have heard the terms microscale or nanoscale to represent the sizes of small objects. What units of length do you think are useful at these scales? What fractions of the fundamental unit of length are these units?
- Acceleration is defined as a change in velocity per time. Propose a unit for acceleration in terms of the fundamental SI units.
- Density is defined as the mass of an object divided by its volume. Propose a unit of density in terms of the fundamental SI units.
Answers
-
- boxes of crayons
- grams of gold
-
- seconds
- metres
-
- 1,000 ×
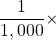
- 1,000,000 ×
-
- milli-
- kilo-
- giga-
-
Unit Abbreviation kilosecond ks millilitre mL megagram Mg centimetre cm
-
- 3.44 μs
- 3.5 kL
- 4.5 cm
-
- 43.6 L
- 4.4 µm
- 1.438 s
- megabytes (Mb)
- metres/second2
- The letter μ is the Greek letter lowercase equivalent to an m and is called “mu” (pronounced “myoo”). ↵
One of the seven basic units of SI used in science.
A prefix used with a unit that refers to a multiple or fraction of a fundamental unit to make a more conveniently sized unit for a specific quantity.
A unit that is a product or a quotient of a fundamental unit.

