Chapter 6. Gases

Molecular Effusion and Diffusion

Learning Objectives

  1. Explore the nature of gas movement: molecular effusion and diffusion.
  2. Examine and apply Graham’s law of effusion.

Effusion

The movement of gas molecules can be divided into a few different types. Effusion is the movement of gas molecules from one container to another via a tiny hole. Typically the container to which the gas is moving is kept under lower pressure.

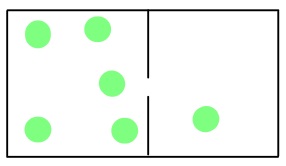
5 molecules sit in 1 part of a divided box and 1 molecule sits in the other. A gap connects the parts.
Figure 6.10 “Molecular Effusion.”

In 1846, the Scottish chemist Thomas Graham found that the rate of effusion of a gas (the amount of gas transferred between containers in a certain amount of time) is inversely proportional to the square root of its molar mass. This means that gases with a lighter molecular weight have higher effusion rates.

Portrait of Thomas Graham.
Figure 6.11 “Thomas Graham.” Graham proposed his law of effusion in 1846.

This finding is summarized in Graham’s law of effusion:

\dfrac{\text{Rate of Effusion (Gas 1)}}{\text{Rate of Effusion (Gas 2)}}=\sqrt{\dfrac{M_2}{M_1}}

This finding can be rationalized by thinking through the process of effusion on the molecular level. For a gas molecule to successfully move from one container to another, it must hit and pass through the tiny hole present in the container. Gases with higher rms speed are more likely to hit and pass through the hole so effusion is dependent on rms speed:

\dfrac{\text{Rate of Effusion (Gas 1)}}{\text{Rate of Effusion (Gas 2)}}=\dfrac{\sqrt{\dfrac{3RT}{M_1}}}{\sqrt{\dfrac{3RT}{M_2}}}=\sqrt{\dfrac{M_2}{M_1}}

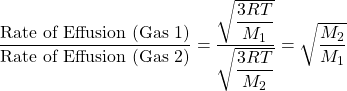
Example 6.20

Problem

An unknown halogen (diatomic) gas effuses at a rate that is approximately 1.89 times the rate of I2 gas at the same temperature. Determine the molar mass and identity of this unknown gas.

Solution

\begin{array}{rrl} \dfrac{\text{Rate of Effusion (Gas 1)}}{\text{Rate of Effusion (Gas 2)}}&=&\sqrt{\dfrac{M_2}{M_1}} \\ \\ \dfrac{\text{Rate of Effusion (Gas \ce{I2})}}{\text{Rate of Effusion (Gas 2)}}&=&\sqrt{\dfrac{M_2}{M\ce{I2}}}}=\dfrac{1}{1.89}=\sqrt{\dfrac{M_2}{253.80\text{ g/mol}}} \\ \\ 0.279&=&\dfrac{M_2}{253.80\text{ g/mol}} \\ \\ M_2&=&71.1\text{ g/mol} \end{array}

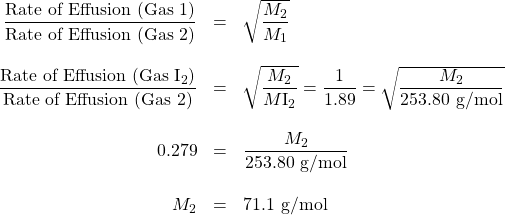
Therefore, the unknown gas is Cl2.

Diffusion

Another type of gas movement is called diffusion; it is the movement of gas molecules through one or more additional types of gas via random molecular motion. Similar to effusion, gases with lower molecular weights (which have a higher rms speed) diffuse faster than gases with higher molecular weights. However, in diffusion, movement is much more complicated as collisions occur between molecules that change the direction and speed of the molecules. As a result of these collisions, the path a molecule travels in diffusion is made up of numerous straight, short segments. The term mean free path is used to describe the average distance travelled by a molecule between collisions.

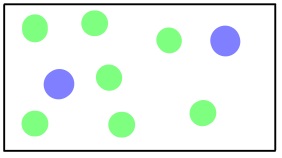
One gas is dispersed throughout another.
Figure 6.12 “Molecular Diffusion.”
Particle mean free path.
Figure 6.13 “Particle Mean Free Path.” Stylized depiction of the path travelled by a gas particle during diffusion. Other particles have been omitted for clarity.

View this video on diffusion by Dr. Jessie A. Key for more information.

Key Takeaways

  • Effusion is the movement of gas molecules from one container to another through a tiny hole.
  • Rates of effusion can be compared at the same temperature using Graham’s law.
  • Diffusion  is the movement of gas molecules through one or more other types of gas via random molecular motion.
  • Both the rates of effusion and diffusion are influenced by the molecular weight of the gas particle

Media Attributions

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introductory Chemistry - 1st Canadian Edition Copyright © 2014 by Jessie A. Key is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book