Chapter 4: Inequalities
4.3 Linear Absolute Value Inequalities
Absolute values are positive magnitudes, which means that they represent the positive value of any number.
For instance, | −5 | and | +5 | are the same, with both having the same value of 5, and | −99 | and | +99 | both share the same value of 99.
When used in inequalities, absolute values become a boundary limit to a number.
Example 4.3.1
Consider [latex]| x | < 4.[/latex] This means that the unknown [latex]x[/latex] value is less than 4, so [latex]| x | < 4[/latex] becomes [latex]x < 4.[/latex] However, there is more to this with regards to negative values for [latex]x.[/latex] | −1 | is a value that is a solution, since 1 < 4. However, | −5 | < 4 is not a solution, since 5 > 4. The boundary of [latex]| x | < 4[/latex] works out to be between −4 and +4. This means that [latex]| x | < 4[/latex] ends up being bounded as [latex]-4 < x < 4.[/latex] If the inequality is written as [latex]| x | \le 4[/latex], then little changes, except that [latex]x[/latex] can then equal −4 and +4, rather than having to be larger or smaller. This means that [latex]| x | \le 4[/latex] ends up being bounded as [latex]-4 \le x \le 4.[/latex]
Example 4.3.2
Consider [latex]|x|[/latex] > [latex]4.[/latex]
This means that the unknown [latex]x[/latex] value is greater than 4, so [latex]|x|[/latex] > [latex]4[/latex] becomes [latex]x[/latex] > [latex]4.[/latex] However, the negative values for [latex]x[/latex] must still be considered.
The boundary of [latex]|x|[/latex] > [latex]4[/latex] works out to be smaller than −4 and larger than +4.
This means that [latex]|x|[/latex] > [latex]4[/latex] ends up being bounded as [latex]x < -4 \text{ or } 4 < x.[/latex] If the inequality is written as [latex]| x | \ge 4,[/latex] then little changes, except that [latex]x[/latex] can then equal −4 and +4, rather than having to be larger or smaller. This means that [latex]|x| \ge 4[/latex] ends up being bounded as [latex]x \le -4 \text{ or } 4 \le x.[/latex]
When drawing the boundaries for inequalities on a number line graph, use the following conventions:
For ≤ or ≥, use [brackets] as boundary limits.![]()
For < or >, use (parentheses) as boundary limits. ![]()
| Equation | Number Line |
|---|---|
| [latex]| x | <4[/latex] |  |
| [latex]| x | \le 4[/latex] |  |
| [latex]| x |[/latex] > [latex]4[/latex] |  |
| [latex]| x | \ge 4[/latex] |  |
When an inequality has an absolute value, isolate the absolute value first in order to graph a solution and/or write it in interval notation. The following examples will illustrate isolating and solving an inequality with an absolute value.
Example 4.3.3
Solve, graph, and give interval notation for the inequality [latex]-4 - 3 | x | \ge -16.[/latex]
First, isolate the inequality:
[latex]\begin{array}{rrrrrl} -4&-&3|x|& \ge & -16 &\\ +4&&&&+4& \text{add 4 to both sides}\\ \hline &&\dfrac{-3|x|}{-3}& \ge & \dfrac{-12}{-3}&\text{divide by }-3 \text{ and flip the sense} \\ \\ &&|x|&\le & 4 && \end{array}[/latex]
At this point, it is known that the inequality is bounded by 4. Specifically, it is between −4 and 4.
This means that [latex]-4 \le | x | \le 4.[/latex]
This solution on a number line looks like:

To write the solution in interval notation, use the symbols and numbers on the number line: [latex][-4, 4].[/latex]
Other examples of absolute value inequalities result in an algebraic expression that is bounded by an inequality.
Example 4.3.4
Solve, graph, and give interval notation for the inequality [latex]| 2x - 4 | \le 6.[/latex]
This means that the inequality to solve is [latex]-6\le 2x - 4\le 6[/latex]:
[latex]\begin{array}{rrrcrrr} -6&\le & 2x&-&4&\le & 6 \\ +4&&&+&4&&+4 \\ \hline \dfrac{-2}{2}&\le &&\dfrac{2x}{2}&&\le & \dfrac{10}{2} \\ \\ -1 &\le &&x&&\le & 5 \end{array}[/latex]

To write the solution in interval notation, use the symbols and numbers on the number line: [latex][-1,5].[/latex]
Example 4.3.5
Solve, graph, and give interval notation for the inequality [latex]9 - 2 | 4x + 1 |[/latex] > [latex]3.[/latex]
First, isolate the inequality by subtracting 9 from both sides:
[latex]\begin{array}{rrrrrrr}9&-&2|4x&+&1&>&3 \\ -9&&&&&&-9 \\ \hline &&-2|4x&+&1|&>&-6 \end{array}[/latex]
Divide both sides by −2 and flip the sense:
[latex]\begin{array}{rcc}\dfrac{-2|4x+1|}{-2}&>&\dfrac{-6}{-2} \\ |4x+1|&<&3 \end{array}[/latex]
At this point, it is known that the inequality expression is between −3 and 3, so [latex]-3 < 4x + 1 < 3.[/latex] All that is left is to isolate [latex]x[/latex]. First, subtract 1 from all three parts:
[latex]\begin{array}{rrrrrrr} -3&<&4x&+&1&<&3 \\ -1&&&-&1&&-1 \\ \hline -4&<&&4x&&<&2 \\ \end{array}[/latex]
Then, divide all three parts by 4:
[latex]\begin{array}{rrrrr} \dfrac{-4}{4}&<&\dfrac{4x}{4}&<&\dfrac{2}{4} \\ \\ -1&<&x&<&\dfrac{1}{2} \\ \end{array}[/latex]
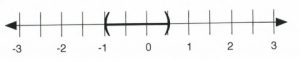
In interval notation, this is written as [latex]\left(-1,\dfrac{1}{2}\right).[/latex]
It is important to remember when solving these equations that the absolute value is always positive. If given an absolute value that is less than a negative number, there will be no solution because absolute value will always be positive, i.e., greater than a negative. Similarly, if absolute value is greater than a negative, the answer will be all real numbers.
This means that:
[latex]\begin{array}{c}| 2x - 4| < -6 \text{ has no possible solution } (x \ne \mathbb{R}) \\ \\ \text{and}\\ \\ |2x-4| > -6 \text{ has every number as a solution and is written as } (-\infty, \infty) \end{array}[/latex]
Note: since infinity can never be reached, use parentheses instead of brackets when writing infinity (positive or negative) in interval notation.
Questions
For questions 1 to 33, solve each inequality, graph its solution, and give interval notation.
- [latex]| x | < 3[/latex]
- [latex]| x | \le 8[/latex]
- [latex]| 2x | < 6[/latex]
- [latex]| x + 3 | < 4[/latex]
- [latex]| x - 2 | < 6[/latex]
- [latex]| x - 8 | < 12[/latex]
- [latex]| x - 7 | < 3[/latex]
- [latex]| x + 3 | \le 4[/latex]
- [latex]| 3x - 2 | < 9[/latex]
- [latex]| 2x + 5 | < 9[/latex]
- [latex]1 + 2 | x - 1 | \le 9[/latex]
- [latex]10 - 3 | x - 2 | \ge 4[/latex]
- [latex]6 - | 2x - 5 |[/latex] > [latex]3[/latex]
- [latex]| x |[/latex] > [latex]5[/latex]
- [latex]| 3x |[/latex] > [latex]5[/latex]
- [latex]| x - 4 |[/latex] > [latex]5[/latex]
- [latex]| x + 3 |[/latex] > [latex]3[/latex]
- [latex]| 2x - 4 |[/latex] > [latex]6[/latex]
- [latex]| x - 5 |[/latex] > [latex]3[/latex]
- [latex]3 - | 2 - x | < 1[/latex]
- [latex]4 + 3 | x - 1 | < 10[/latex]
- [latex]3 - 2 | 3x - 1 | \ge -7[/latex]
- [latex]3 - 2 | x - 5 | \le -15[/latex]
- [latex]4 - 6 | -6 - 3x | \le -5[/latex]
- [latex]-2 - 3 | 4 - 2x | \ge -8[/latex]
- [latex]-3 - 2 | 4x - 5 | \ge 1[/latex]
- [latex]4 - 5 | -2x - 7 | < -1[/latex]
- [latex]-2 + 3 | 5 - x | \le 4[/latex]
- [latex]3 - 2 | 4x - 5 | \ge 1[/latex]
- [latex]-2 - 3 | - 3x - 5| \ge -5[/latex]
- [latex]-5 - 2 | 3x - 6 | < -8[/latex]
- [latex]6 - 3 | 1 - 4x | < -3[/latex]
- [latex]4 - 4 | -2x + 6 |[/latex] > [latex]-4[/latex]

